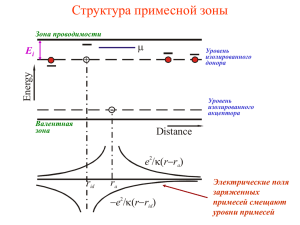
Слабая локализация

Квантовые поправки к
проводимости
(в грязных металлах)
Слабая локализация
и
межэлектронное взаимодействие
ne 2l

k F
Два типа электронного рассеяния:
Упругое с вероятностью 1/t
Выражение для фазы j
волновой функции
  exp( it / )
сохраняется:
j  t / 
Неупругое с вероятностью 1/tj
t << tj
- диффузия
Слабая локализация
(4Dt )
d
2
 r2 
exp  
,
 4 Dt 
d
r 2   xi2
2
p(r,t)= (4Dt)1exp (r2/4Dt)
i 1
2
1
2
l
Коэффициент диффузии D  lv  tv 
t
d
4Dt1 p(r,t)
p( r, t ) 
1
t =t1
(<tj)
1
t = 2t1
(>tj)
Ширина распределения после N шагов
t  20 t
l N  l t  Dt  LN
t
0
3
2
1
0
1
1/2
r /(4Dt1)
t  10 t
Без интерференции
|A1+A2|2 =
= |A1|2+|A2|2 +2A1A2 = 4A2
C интерференцией
t  10 t
|A1|2+|A2|2= 2A2
2
3
Вычисления
d=3
tj

vF 2dt
vF 2 1 2 1 2
1  1 1 
 
 tj )  2   
3 
3 (t
2

k F l  Lj l 
D2
t ( Dt )
Lj  диффузионная длина:
tj 
Lj  Dtj  l N  l ( tj t)
1
2
диффузионное время
tj
d=2
const !!

vF  dt
vF  tj
 

ln
t

(
Dt
)
b
Db
t
tj
2
2

vF  dt
vF 
d=1
 

(l  Lj )
1
2
2 2

Db
t ( Dt ) b
2
2
e 2  1 1 
3    
  Lj l 
e2 Lj
2   ln
l

e2
1  (l  Lj )

d  b3d
Экспериментальные наблюдения слабой локализации
R/R = 0,54 %
 =151051
35,2
35,1
1
Cu
T (K)
1
10
Cu  L.Van der Dreis et al., PRL 46, 565 (1981)
5,7210
5,7205
5,7200
Au
Au  С.И.Дорожкин, В.Т.Долгополов.,
Письма в ЖЭТФ 36, 15 (1982)
5,7195
T (K)
10
В формулы для  не входят ни n , ни .
1,9
1,10
, кОм
6,5
1,08
6,0
aInO
a-InO
1,7
1,5
2,7
2,5
1,9
1,06
5,5
1,04
D.J.Bishop, D.C.Tsui,
R.C.Dynes, PRL 44,
1153 (1980)
R (k)
7,0
, кОм
R ()
35,3
R ()
R/R = 0,04 %
 = 71051
5,7215
1,7
1
0,1
T, K
1
Гетероструктуры
Z.Ovadyahu, Y.Imry
PRB 24, 7440 (1981)
5
10
T (K)
50 100
Когерентное рассеяние света назад
q3
Лазер
q2
q4
q1
k
k2
k3
k3
k1
q1
k

k1 k2
q4
Образец
Взвесь полистироловых
шариков   m в воде
Диафрагмы
q2
Стеклянная
пластинка
Поляризатор
q3
Фотоумножитель
Описание слабой локализации
в k-представлении
0,6
Интенсивность
k + q1+ q2 + q3 + q4 =
k + q4+ q3 + q2 + q1 =
k
Линза
P.Wolf, G.Maret,
PRL 55, 1153
(1985)
a
0,4
0,2
0
2
b
c
1
Интерференционный
фильтр
0
 (градусы)
1
2
Разрушение слабой локализации магнитным полем t << 1
При обходе замкнутой диффузионной траектории площадью S
 iBS 
 e

,  0  c
   exp  i  Adl    exp  
e
 c

 0 
У обходов в противоположных направлениях появляется разность фаз j
= 2 (BS/0)
Средняя площадь S и поток BS через нее зависят от времени:
B S  Br  Bl 2
2
t
t
Поскольку у всех диффузионных траекторий площади S разные,
слабая локализация разрушается. Разрушающее поле
Bj 
c
( Dtj ) 1
e
Со своей стороны, поле определяет магнитную длину и магнитное время

l B  c

2eB
1
2
 0 lB2
tB 
  1 (k F l ) 1
BD D
Разрушение слабой локализации магнитным полем t << 1
(эксперимент)
При вычислении
квантовой поправки
нужно заменить верхний
предел интегрирования
tj
Mg
169,0
tB

t
R ()
168,5
t
Например, при d=2
e2 Lj
( B )  (0)  2 ln
 lB
l  lB  Lj
4,4 K
168,0 6,2
8,1
12,1
17,1
28,7
167,5
 8 6  4  2
0 2
B(T )
4
6
G.Bergmann, Phys.Rep. 107, 1 (1981)
Магнетосопротивление цилиндрических пленок
R, Ом
R, Ом
R, Ом
Mg
G, Ом
1
1
R, Ом
Li
Al
7
0,01
0,1
10
0,3
0,1
10
9
1,425 K
G, Ом
R = 1245 Ом
2r = 1,10 мкм
0,2
0
0,1
T = 1,1 K
2r = 1,6 мкм
0
20
B, Э
40
0
1,502 K
T = 1,1 K
2r = 1,3 мкм
R = 2 кОм
0
20 40
B, Э
Д.Ю. Шарвин, Ю.В. Шарвин и др.,
Письма в ЖЭТФ 34, 285 (1981);
35, 476 (1982).
1,715 K
60
0
10
B, Э
20
M.Gijs, C. Van Haesendonck,
Y. Bruynseraede,
PRB 30, 2964 (1984).
Антилокализация
Магнитный момент m, движущийся со скоростью v, создает электрическое
поле e  [mv]. А в металле есть свои электрические поля (ядра с зарядом Ze !).
Отсюда спин-орбитальное взаимодействие: на движущийся спин действует сила.
Из-за этого взаимодействия есть конечная вероятность того, что при рассеянии на
немагнитной примеси произойдет еще и переворот спина
t so1
0
t
1
2
e

~ ( Z)  1,
4
t
c

1
137
tso
Волновая функция двух электронов имеет вид столбца
 0  


 1, 1  




 1,0  
   
 1,1  
(j(1)j(2 )  j(1)j(2 ) ) 


j(1)j(2 )

(
1
)
(
2
)
(
1
)
(
2
)
1
(j  j   j  j  ) 
2

(1) ( 2 )
j j

1
2
t
tj
t
tso
tj
tj
d
vF 2dt  3  t tso 1 
 
e
 ,

d
2 3d  2

2
t ( Dt ) b
R, Ом
98,3
98,2
4,5 K
98,1 6,5
9,5
14,1
2%
0
3,8
 0,1
4 2
0
2
B, Тл
4
6
16% Au
8%
4%
7,1
R =91 Ом
T =4,6 K
tj tso
98,0 20,1
6
d  1, 2, 3
Au
Mg
54
27
0,1
14
Cu
R, Ом
0
t
 0,8
0% Au
0,5
 0,4
G.Bergmann, Phys.Rep. 107, 1 (1981)
1%
0
B, Тл
0,4
0,8
Спин-орбитальное взаимодействие определяется произведением
E e  E [mv]. Кристаллическое (и вообще, внешнее) поле входит
в это выражение дважды, через E и через v.
В гетероструктурах
это приводит к зависимости от степени асимметрии ямы
20
InGaAs /InP
0
GaAs /AlGaAs
10
100 mV
1
15
 (M)
2
 в единицах e /h
Vg = 200 mV
 0,3 V
 0,2 V
30
 0,1 V
T = 1,4 K
45
10
0
B, мТл
0 mV
50 mV
100 mV
0V
20
Vg = 0,1 V
2
0
2
S.A. Studenikin et al.,
Письма в ЖЭТФ 77, 362 (2003)
150 mV
 0,4
 0,2
0
B (mT)
0,2
J.B. Miller et al.,
PRL 90, 076807 (2003)
0,4
ее - взаимодействие (интерференция)
Баллистический режим
r ~ vF t
Диффузионный режим
r ~ l t t ~ vF tt
Фаза
L
exp (ij)  exp[ i( i )t ], j  (  )t
Время расфазировки
tee ~  
 ~ T
Длина расфазировки
Lee  l
tee ~  T
tee
t
D
 vF

t
T
T
Диффундирующие электроны в течение времени tee сохраняют
когерентность, расходясь за это время на расстояние Lee .
Влияние диффузии на частоту ее-столкновений
Баллистический режим
1
1’
2

2’
2
T
~
te
F
Диффузионный режим
Размер области взаимодействия Lee>>1/kF , переданный импульс мал :
q  Lee << kF

te
d
q
~
gd
~ 1
gd Ldee
, плотность состояний
1
T t
d

d
2 1 d
~ T F t 2 
te
2
1
2
gd ~ 
3
2 2
2
F
T  t
m
d 1
,
T F1t1 ,
3
d 1
2
F
d 2
,
d 3
1
2
Квантовая поправка к проводимости
от межэлетронной интерференции
g ()
Основное влияние
ее-взаимодействия на транспорт
осуществляется за счет
особенности в плотности
состояний
h/t
gF
|F|
e  1 1
 ee 3  
 
  Lee l 
2
e2 Lee
 ee 2   ln
l

e2
 ee 1  (l  Lee )

T2 >T1
T1
F
T
vF 2dt
 ( Dt )
t
d
2
b
3 d
,

d  1, 2, 3
h/Ft
1
d 1
ee
h/te= (gdL ) +T /F
)
T
(
=
h/t
tee= h/T > t
T
=
t
h/
0
2 1
F
2
/3
h/te= T 2/F
tee= h/T< t
T/F
1
Выводы ...
F
Localization ??
300
=h
T,
=
h/t ph
Ziman
theory
F /10
en
s
i
e
ün
r
G
Resistivity  (m·cm)
Tt

1
Scattering rate h/t
Mooij rule
1
<
n
tio
c
fun
30
h/t0
0
F /10
... и планы
Temperature T
F
K
Cu
Al
Sn
W
Pb
Ag
 (экспер.)
1.75
1.35
0.4
0.07
0.2
0.1
1.5
0
( Что делать, чтобы добиться локализации ? )