ТОПОЛОГИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Электрические схемы. Основные определения

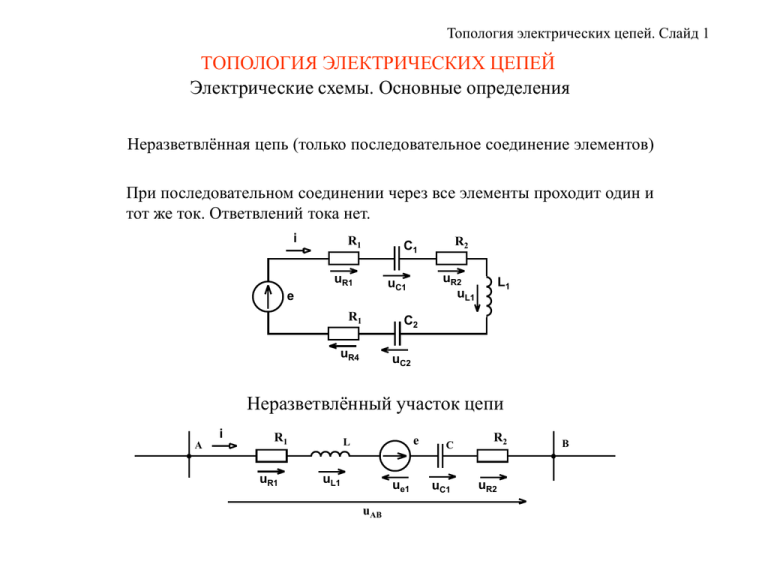
Топология электрических цепей. Слайд 1
ТОПОЛОГИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Электрические схемы. Основные определения
Неразветвлённая цепь (только последовательное соединение элементов)
При последовательном соединении через все элементы проходит один и
тот же ток. Ответвлений тока нет.
i
R1
R2
C1
uR1
uR2
uL1
uС1
е
R1
L1
C2
uR4
uС2
Неразветвлённый участок цепи
i
A
R1
uR1
e
L
uL1
ue1
uAB
C
uС1
R2
uR2
B
Топология электрических цепей. Слайд 2
Разветвлённая цепь (параллельное соединение)
i
A
i1
i2
L2
R1
e
i3
C3 u
AB
B
i
i
A
е
L2
R1
i1
i2
B
C3
uAB
A
R1
е
i1
i3
B
uAB
L2
i2
uAB
C3
uAB
i3
Топология электрических цепей. Слайд 3
Разветвлённая цепь (смешенное соединение)
i
i
A
R1
R2
j
R1
R3
L2
i1
A
j
C3
L2
i1
i3
i2
R2
i2
B
B
i1
R1
uR1
A
R2
R3
e
L3
i2
i3
B
R4
uAB
C4
i4
R3
uAB
C3
i3
Топология электрических цепей. Слайд 4
Соединение звездой и многоугольником
1
1
R1
R31
4
R3
R2
3
3
R12
2
R23
2
Топология электрических цепей. Слайд 5
Топологические элементы цепей
1. Узел
2. Ветвь
3. Контур.
3.1. Независимый
контур
u21
R2
1
i1
i2
R1
i3
u14
L1
i4
i1
4
i2
2
R3
u23
C3
i4
i3
C4
3
B
u43
Топология электрических цепей. Слайд 6
E1
R1
E2
2
R2
R3
I1
E4
R5
R4
1
3
I4
E6
1
I2
I3
4
I5
I6
R6
4
2
3
6
7
5
Законы Кирхгофа. Слайд 7
Компонентные и топологические уравнения
Компонентные уравнения устанавливают связь между напряжением и током
каждой ветви. Например,
U R 4  R4 I 4
Топологические уравнения отражают свойства цепи, которые определяются
только её топологией и не зависят от того какие элементы входят в состав ветвей.
Например, уравнения, записанные по законам Кирхгофа.
Законы Кирхгофа
Первый закон.
i
K
0
K
Второй закон.
u
K
K
0
или
 u  e
i
i
j
j
Законы Кирхгофа. Слайд 8
ПРИМЕРЫ
Уравнения по первому закону Кирхгофа
A
I1
R1
За положительное принято направление
тока к узлу. Можно было и наоборот.
R2
I2
I3
R3
Для узла А
I1  I 2  I 3  0
Для узла В
 I1  I 2  I 3  0
E2
E1
B
Уравнения по второму закону Кирхгофа
Все контуры обходятся по часовой стрелке. Можно было выбрать направление обхода
для каждого контура отдельно.
A
UR1
R1
R2
UR2
UR3
Для левого контура
E1  E2  U R1  U R 2
Для правого контура
E2  U R 2  U R 3
Для внешнего контура
E1  U R1  U R3
R3
E2
E1
B
Уравнения равновесия электрических цепей. Слайд 9
УРАВНЕНИЯ ЭЛЕКТРИЧЕСКОГО РАВНОВЕСИЯ
Основные задачи теории цепей
Х1(t)
Y1(t)
Х2(t)
Y2(t)
Х (t)
ХN(t)
Электрическая
цепь
Y (t)
YN(t)
Две задачи теории цепей
1. Задача анализа
2. Задача синтеза
Уравнения равновесия электрических цепей. Слайд 10
Уравнения электрического равновесия
В общем случае в цепи, содержащей p ветвей и q узлов, имеется
2р неизвестных токов и напряжений.
Сколько всего надо записать линейно независимых уравнений по законам
Кирхгофа для анализа электрической цепи?
Столько, сколько всего ветвей в схеме ( р уравнений).
Сколько надо записать уравнений по первому закону Кирхгофа (уравнений
баланса токов)?
На одно меньше, чем количество узлов в схеме ( m=q-1 уравнение).
Сколько надо записать уравнений по второму закону Кирхгофа (независимых
уравнений баланса напряжений)?
Все остальные недостающие до р (n=p-q+1 уравнение).
Всего р=n+m топологических уравнений. Да ещё р компонентных уравнений для
нахождения напряжений на ветвях. Всего 2р уравнений.
Если в цепи имеется рИТ ветвей содержащих только идеализированные источники
тока, и рИН ветвей, содержащих только идеализированные источники напряжения,
то компонентных уравнений надо составить р – рИТ -рИН. Значит всего 2р – рИТ –
рИН уравнений.
Законы Кирхгофа. Слайд 11
Примеры
A
I1
R1
i1
R2
I2
R3
I3
R1
A
R2
uR1
R3
e
E2
E1
L3
i2
i3
B
B
E1
R1
E2
2
R2
R3
I1
I2
I3
E4
R5
R4
1
3
I4
E6
4
I5
R6
I6
R4
uAB
C4
i4