task_16933x

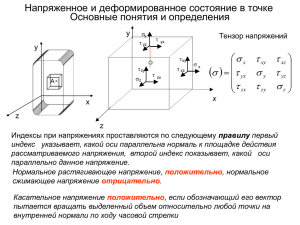
Контрольная работа №1
На рис.2.37 даны схемы, на вход которых воздействует одно из
периодических напряжений u(t) (графики напряжений приведены на рис. 2.38
– 2.45). Схемы нагружены на активное сопротивление нагрузки Rн.
Численные значения напряжения Um, периода Т, параметров схемы L, C и
величины активного сопротивления нагрузки Rн приведены в таблице 2.2.
Требуется:
1. Разложить напряжение u(t) в ряд Фурье до пятой гармоники
включительно, используя табличные разложения, приведенные в
учебниках, и пояснение, имеющееся в указаниях к данной задаче.
2. Обозначив сопротивления элементов схемы в общем виде как Rн,
jXL, –jXС, вывести формулу для комплексной амплитуды
 через комплексную амплитуду
напряжения на нагрузке U
2m
 . Полученное напряжение пригодно для
входного напряжения U
1m
каждой гармоники, только под XL и XC следует понимать
сопротивления для соответствующей гармоники.
3. Используя формулы п. 2, определить комплексную амплитуду
напряжения на выходе (на нагрузке) для следующих гармоник ряда
Фурье: для нулевой, первой и третьей гармоник в схемах рис.
2.37,в,г; для первой, третьей и пятой гармоник в схемах рис. 2.
37,а.б.
4. Записать мгновенное значение напряжения на нагрузке u2 = f(t) в
виде ряда Фурье.
У к а з а н и е:
На примере рис. 2.44, 2.45 покажем как осуществляется разложение в
ряд Фурье кривых, которые имеют постоянную составляющую и начало
которых сдвинуто во времени по отношению к табличным кривым. Прежде
всего выделим в напряжении u1(t) (рис.2.45) постоянную составляющую Um/2
и мысленно проведем новую ось времени на высоте Um/2. Тогда
относительно новой оси времени оставшуюся часть напряжения запишем в
виде
4U m
2
T
1
3t
1
5t


cos t  sin
cos 3t  sin
cos 5t  .
 sin
12
3
12
5
12


Здесь под Um понимается амплитуда заданного напряжения, а угол
Т/12 равен углу, обозначенному в учебниках . С учетом постоянной
составляющей u1(t) (рис 2.45) раскладывается в ряд Фурье следующим
образом:
U
2U m  1
1

cos 5t  ... .
u1(t) = m 
 cos t  cos 3t 
2
 2
52

График напряжения u1(t) (рис.2.44) на время Т/4 смещен (запаздывает)
во времени, поэтому для рис. 2.44
U
4U m
T
T 1
3t
T


u 1 (t)  m 
 [sin
cos  t    sin
cos 3 t   
2
2
12
4 3
12
4


1
5t
T

 sin
cos 5 t    ...]
5
12
4

или
U m 2U m
1
1
1

 [ sin t  sin 3t 
sin 5t  ...].
2

2
3
52

Покажем, как вывести формулу для напряжения на выходе схемы U
2m
 на примере рис.2 46.
через параметры схемы и напряжение на входе U
u 1 (t) 
1m
Запишем уравнение по второму закону Кирхгофа:
 1m  I 1m  R 1  I 2 m  ( jX C )  U
 2m .
U
 :
Выразим токи I и I через напряжение U
1m
2m
2m

 2 m  U 2 m  ( jX C )
U


Rн
I 2 m  U 2 m ;
I 1m  U 2 m 
Rн
Rн
jX L
и подставим в исходное выражение, тогда
jX L  R н
 2m  U
 1m 
U
.
R 1  R н  X L  X C  j(R 1  X L  R 1  X C  X L  R н )
Таблица 2.2.
Исходные данные по вариантам к задаче контрольного задания 1.
Вариант
L, мГн
С, мкФ
Т, 10-3 с
Um, В
Rн Ом
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1,44
11
0,5
0,4
0,7
5
5,6
2,52
4,2
20
1
20
1,5
2,58
3
5,4
6,25
6,25
0,5
0,7
1,6
0,8
4
0,4
0,5
0,24
1
2,28
1,4
1,44
1
1
8
0,3
1,43
0,9
3
12,4
10
0,4
0,875
0,89
0,48
2
0,167
0,159
0,134
0,625
1,2
0,63
0,8
1,67
0,314
5,88
0,354
0,483
0,565
1,34
3,13
2,5
0,167
0,277
0,536
12
100
50
50
45
25
48,5
17
40
80
100
30
33
40
75
40
12,78
40
70
110
70
35,4
65,7
27
36,4
41,4
86,5
38,6
55
41,4
185
25
59
64,5
49,6
44,7
55,2
17,5
31,5
27
36,4
35,4
Рисунок с
изображени
ем схемы
2.37,б
2.37,в
2.37,г
2.37,а
2.37,б
2.37,в
2.37,г
2.37,а
2.37,б
2.37,в
2.37,г
2.37,а
2.37,б
2.37,в
2.37,г
2.37,а
2.37,б
2.37,в
2.37,г
2.37,а
2.37,б
Рисунок с
графиком
u1(t)
2.43
2.42
2.41
2.39
2.40
2.43
2.42
2. 42
2.41
2.40
2.43
2.43
2.38
2.45
2.38
2.44
2.39
2.40
2.43
2.41
2.39
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
9,57
0,55
0,357
0,62
4,35
6,15
2,9
2,92
23
1,15
16,7
1,72
1,95
3,6
5,94
5,68
6,87
0,625
0,65
3,48
0,44
0,447
0,212
0,87
2,5
1,61
1
1,15
1,15
6,67
0,334
1,08
1,08
3,3
11,27
11
0,5
0,81
1,74
0,184
0,142
0,118
0,544
1,33
0,725
0,555
1,92
0,362
4,9
0,416
0,365
0,678
1,47
2,84
2,75
0,209
0,257
18,85
104,6
33,4
150
15
26,2
76
17
13,35
102,2
104,5
141
100
37,5
60
60
40
44,7
110
65,7
27
36,4
41,4
86,5
38,6
55
41,4
185
25
59
64,5
49,6
44,7
55,2
17,5
31,5
27
36,4
2.37,в
2.37,г
2.37,а
2.37,б
2.37,в
2.37,г
2.37,а
2.37,б
2.37,в
2.37,г
2.37,а
2.37,б
2.37,в
2.37,г
2.37,а
2.37,б
2.37,в
2.37,г
2.37,а
2.38
2.38
2.41
2.38
2.39
2.40
2. 44
2.39
2.44
2.39
2.41
2.40
2.43
2.40
2.40
2.39
2.42
2.43
2.43
Рисунки к вариантам задачи контрольного задания 1.
C
C
C
а)
u1(t)
u2(t)
L
L
б)
u1(t)
L u2(t)
L
L
L
в)
C
u1(t)
г)
C
u1(t) C
u2(t)
u2(t)
Рис.2.37
U1(t)
U1(t)
Um
Um
t
t
0
T/6
T/3
0
T
T/2
T/4
U1(t)
T
u1(t)
Um
Um
t
T/4
3T/4
Рис. 2.39.
Рис. 2.38.
0
T/2
T/2
3T/4
Рис. 2.40.
T
0
T/4
T/2 3T/4
Рис.2.41.
t
T
u1(t)
u1(t)
Um
Um
t
t
0
T/2
0
T
T/4
T/2
3T/4
T
Рис.2.43
3.
Рис.2.42.
u1(t)
u1(t)
Um
Um
t
t
0
0 T/12 T/4
T
T/6 T/3 T/2
T/2
Рис. 2.45.
Рис.2.44.
I
1m

U
1m

–jXC I 2 m
R1
jXL
Рис. 2.46.
Rн

U
2m
3T/4
T