Лаба № 1
реклама
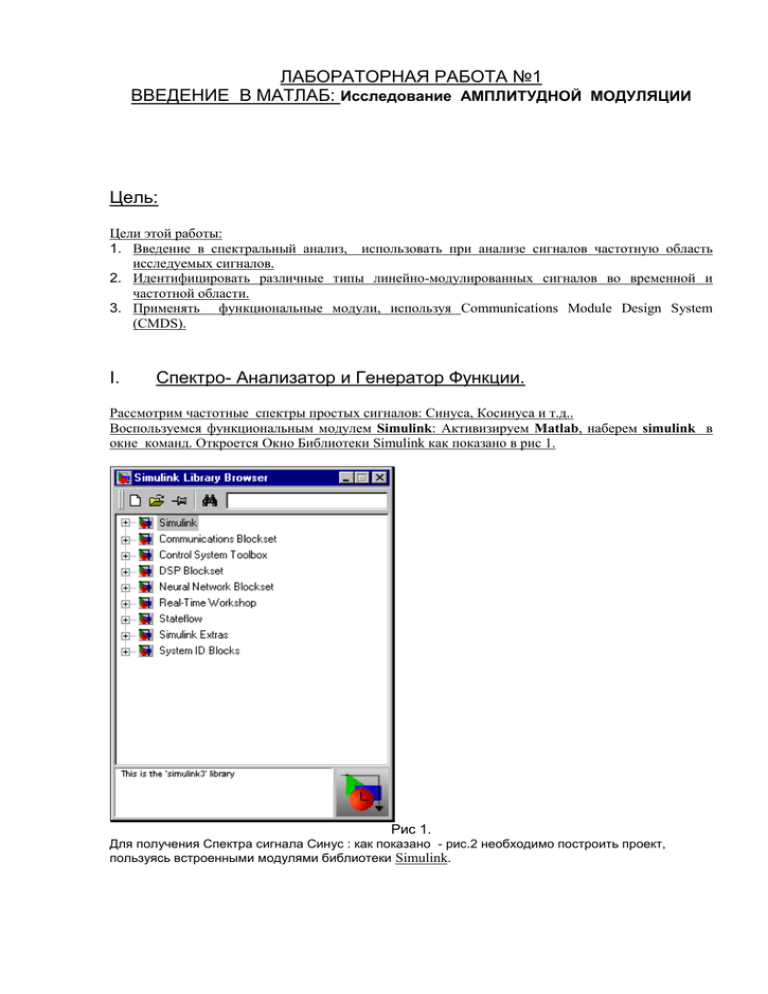
ЛАБОРАТОРНАЯ РАБОТА №1 ВВЕДЕНИЕ В МАТЛАБ: Исследование АМПЛИТУДНОЙ МОДУЛЯЦИИ Цель: Цели этой работы: 1. Введение в спектральный анализ, использовать при анализе сигналов частотную область исследуемых сигналов. 2. Идентифицировать различные типы линейно-модулированных сигналов во временной и частотной области. 3. Применять функциональные модули, используя Communications Module Design System (CMDS). I. Спектро- Анализатор и Генератор Функции. Рассмотрим частотные спектры простых сигналов: Синуса, Косинуса и т.д.. Воспользуемся функциональным модулем Simulink: Активизируем Matlab, наберем simulink в окне команд. Откроется Окно Библиотеки Simulink как показано в рис 1. Рис 1. Для получения Спектра сигнала Синус : как показано - рис.2 необходимо построить проект, пользуясь встроенными модулями библиотеки Simulink. Рис.2 Расположение используемых блоков: 1. - 2 3 Для получения блока B-FFT необходимо в свойствах блока FFT поставить галочку на сводку “Buffer input” Продемонстрировано умножение двух идентичных сигналов синуса1kHz. Поведение сигнала во временной и частотной областях при разных значениях km. Рис.2 Рис.3 показывает сигнал синуса во временной области, а соответствующая область частоты показана рис.4. Спектр в частотной области получен через buffered-FFT(B-FFT) (возможности, которого включают Быстрое Fourier Преобразование, из 128 отчетов), который использует buffering 64 из них в одном модуле. Блок B-FFT также показан в Рис. 5. Рис.3 Рис.4 Рис.5 Параметры B-FFT, свойства осей графиков, свойства Линии могут быть изменены. Частотный диапазон может быть изменен при использовании меню, а значения коэффициентов на оси Y могут быть измерены в реальном масштабе или на децибелах. Время осуществления выборки в этом случае выбрано 1/5000. Внимание: частота осуществления выборки возможностей B-FFT должна соответствовать времени осуществления выборки сигнала. Также как обозначено выше FFT взят для 128 точек и buffered с половиной из них для выполнения алгоритма вычисления. Вычисление Мощности: мощность может быть вычислена возведением в квадрат амплитуды напряжения в спектре. Подобные операции могут быть сделаны для других видов сигналов( они могут быть сгенерированы от блока генератора сигналов). Модуляция Уравнение для амплитудной модуляции можно записать: y = kmcos2 (2P (1 000) t), представлено на рис. 6. рис.6 Тогда км может быть вычислен как: km Vpp(2kHz) * 2 0.5 / 2 * 2 0.5 Vpp(1kHz) Модель анализатора спектра для km=1 показано ниже. Рис.7 На рис.7 продемонстрировано умножение двух идентичных сигналов синуса 1kHz. ЗАДАНИЕ 1. Необходимо построить модель АМ-модулятора, проанализировать поведение сигнала во временной и частотной областях при разных значениях km. 2. ИЗУЧИТЬ ПОВЕДЕНИЕ Сигналов в частотной и временной области : А) синус или косинус, Б) треугольный, Г) прямоугольный.











