Документ 327860

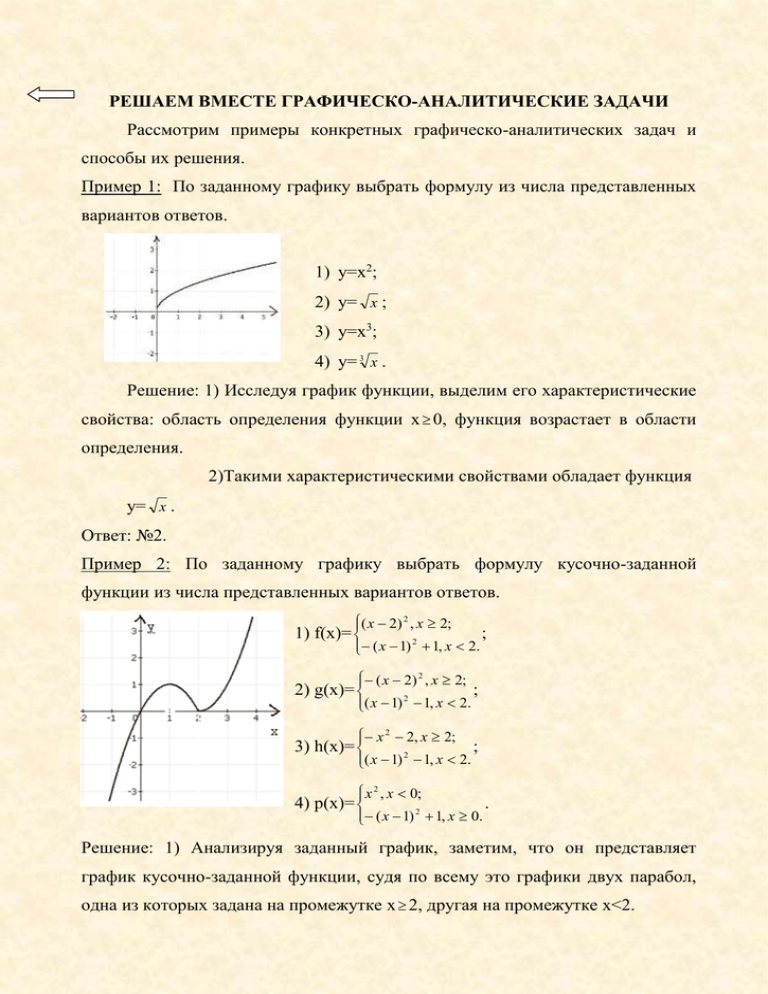
РЕШАЕМ ВМЕСТЕ ГРАФИЧЕСКО-АНАЛИТИЧЕСКИЕ ЗАДАЧИ
Рассмотрим примеры конкретных графическо-аналитических задач и
способы их решения.
Пример 1: По заданному графику выбрать формулу из числа представленных
вариантов ответов.
1) у=х2;
2) у= х ;
3) у=х3;
4) у= 3 х .
Решение: 1) Исследуя график функции, выделим его характеристические
свойства: область определения функции х  0, функция возрастает в области
определения.
2)Такими характеристическими свойствами обладает функция
у= х .
Ответ: №2.
Пример 2: По заданному графику выбрать формулу кусочно-заданной
функции из числа представленных вариантов ответов.
( х  2) 2 , х  2;
1) f(x)= 
;
 ( х  1) 2  1, х  2.
 ( x  2) 2 , x  2;
2) g(x)= 
;
( х  1) 2  1, x  2.
 х 2  2, х  2;
3) h(x)= 
;
( х  1) 2  1, x  2.
 х 2 , х  0;
4) p(x)= 
.
 ( х  1) 2  1, x  0.
Решение: 1) Анализируя заданный график, заметим, что он представляет
график кусочно-заданной функции, судя по всему это графики двух парабол,
одна из которых задана на промежутке x  2, другая на промежутке x<2.
2) При x<2 видим, что ветви параболы y1=а1(x-x0)2+y0 направлены
вниз, следовательно, a1<0. Используя график, можно заметить, что вершина
параболы находится в точке (1;1), следовательно, х0=1, у0=1, а=-1, т.е.
у1=-(х-1)2+1.
3) Аналогично, рассуждая, при х  2, отметим, что ветви параболы
y2=а2(x-x0)2+y0 направлены вверх, следовательно, a>0, а вершина параболы
находится в точке (2;0), отсюда следует, что х0=2, у0=0, а2=1. Тогда у2=(х-2)2.
( х  2) 2 , х  0;
Тогда y= 
. Следовательно, ответ №1.
 ( х  1) 2  1, х  2.
Пример 3: Задайте формулой функцию, график которой изображен на рисунке.
Решение:
1) Анализируя заданный график, делаем вывод, что это график параболы, т.е.
график квадратичной функции;
2) Выявим существенные свойства, необходимые для записи аналитического
задания параболы: а) ветви параболы направлены вниз; б) вершина параболы в
точке (0;2); в) при х=1, у=1. Делаем вывод, что это может быть график
функции
у=-х2+2.
3) Проверим контрольными точками правильность выбора: х=2  у=-2, х=-2
 у=-2.
Ответ: у=-х2+2.
Пример 4: Задайте формулой функцию, график которой изображен на рисунке.
Решение: 1) Анализируя данный график, делаем вывод, что это
k
x
гипербола у= .
2) Найдем контрольные точки: если х=1, то у=-1; если х=-1, то
1
х
у=1. Делаем вывод, что данный график – график функции у=  .
3) Проверим правильность вывода контрольными точками: при
1
2
1
2
1
2
1
2
х=2, у= ; при х= , у=-1; при х=-2, у=  ; при х=  , у=1.
1
х
Ответ: у=  .
Пример 5: Задайте аналитически функцию, график которой изображен на
рисунке.
Решение:
1)
Анализируя
заданный
график,
замечаем,
что
он
представляет совокупность двух лучей, т.е. состоит из графиков двух
линейных функций, причем одна задана на промежутке х<3, другая на
промежутке х  3.
2) При х<3, линейная функция y=k1x+b1 возрастает, значит k1>0, причем b1=2,
т.е. y=k1x+2. Найдем k1 c помощью какой-нибудь контрольной точки графика,
2
3
например, (-3;0). Получаем 0= k1 (-3)+2  k1= .
3) Аналогично, рассуждая, отметим, что y=k2x+b2 убывает  k2<0, кроме того,
0  k 2  5  b2
. Отсюда следует, что
4  k 2  3  b2
графику принадлежат точки (5;0) и (3;4)  
k2=-2, b=10.
2
х  2, х  3;
Ответ: f(x)=  3
 2 x  10, x  3.
назад