Задание 4 для 10 класса

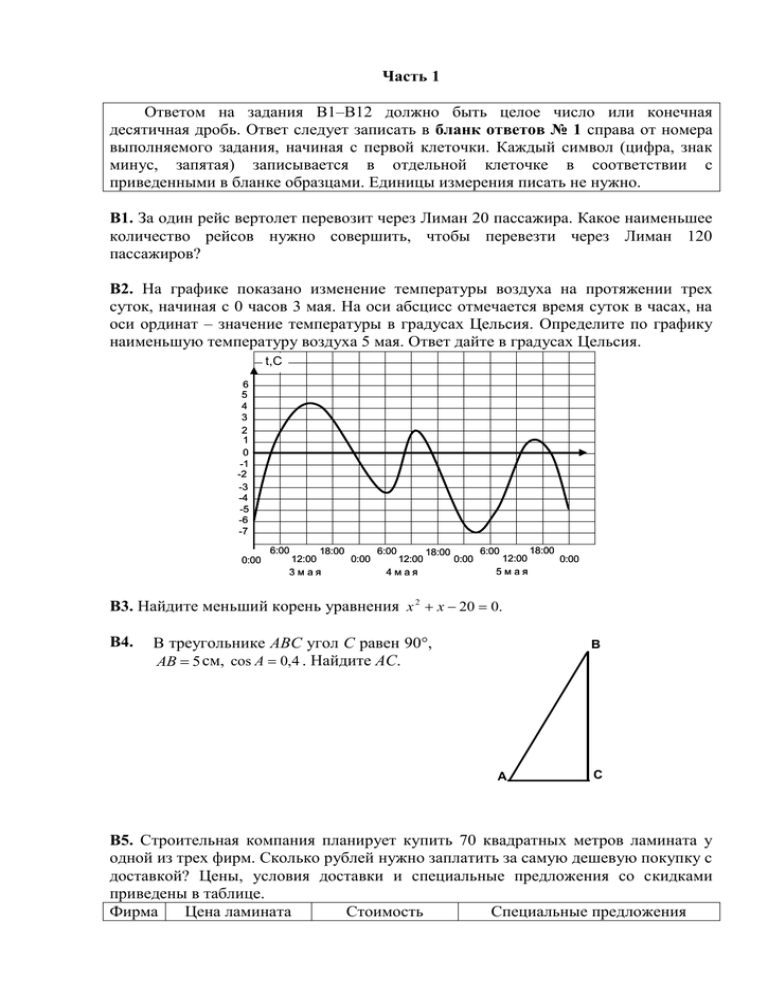
Часть 1
Ответом на задания В1–В12 должно быть целое число или конечная
десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера
выполняемого задания, начиная с первой клеточки. Каждый символ (цифра, знак
минус, запятая) записывается в отдельной клеточке в соответствии с
приведенными в бланке образцами. Единицы измерения писать не нужно.
В1. За один рейс вертолет перевозит через Лиман 20 пассажира. Какое наименьшее
количество рейсов нужно совершить, чтобы перевезти через Лиман 120
пассажиров?
В2. На графике показано изменение температуры воздуха на протяжении трех
суток, начиная с 0 часов 3 мая. На оси абсцисс отмечается время суток в часах, на
оси ординат – значение температуры в градусах Цельсия. Определите по графику
наименьшую температуру воздуха 5 мая. Ответ дайте в градусах Цельсия.
t,C
6
5
4
3
2
1
0
-1
-2
-3
-4
-5
-6
-7
6:00
0:00
18:00
18:00
6:00
6:00
18:00
12:00
12:00
0:00
12:00
0:00
0:00
5мая
3мая
4мая
В3. Найдите меньший корень уравнения x 2  x  20  0.
В4.
В треугольнике ABC угол C равен 90,
AB  5 см, cos A  0,4 . Найдите АC.
В
А
С
В5. Строительная компания планирует купить 70 квадратных метров ламината у
одной из трех фирм. Сколько рублей нужно заплатить за самую дешевую покупку с
доставкой? Цены, условия доставки и специальные предложения со скидками
приведены в таблице.
Фирма
Цена ламината
Стоимость
Специальные предложения
А
(руб. за 1 м2)
610
доставки (руб.)
2900
Б
650
2100
В
640
2300
В6.
Нет
При заказе на сумму более 45000
рублей доставка бесплатно
При заказе на сумму более 50000
рублей доставка бесплатно
Найдите площадь треугольника ABC,
изображенного на клетчатой бумаге,
если площадь одной клетки равна
1см2. Ответ дайте в квадратных
сантиметрах.
В
А
С
В7. Найдите значение выражения 1,5 x 3  0,8 x при х  1 .
В8. Найдите угловой коэффициент касательной к графику функции f x   x 2  3x ,
проходящей через точку М(2; –2).
В9. Дан куб ABCDA1B1C1D1. Найдите тангенс угла между прямыми A1D и B1C1.
В10. От одного села до другого вездеход доехал за 3 часа, а автобус – за 2 часа.
Скорость автобуса на 25 км/ч больше скорости вездехода. Чему равно расстояние
между селами?
3
В11. Найдите значение sin  , если cos   0,8 и    
.
2
В12. На первый курс университета может быть принято 180 человек. Число
поданных заявлений составило 120% от количества мест на курсе. Сколько
заявлений было подано?
Часть 2
Для записи решений и ответов на задания С1–С6 используйте бланк ответов
№2. Запишите сначала номер выполняемого задания, а затем полное обоснованное
решение и ответ.
С1. Решите уравнение
6 cos 2 x  cos x  2
 sin x
 0.
С2. Найдите длину боковой стороны равнобедренной трапеции, основания которой
равны 14 см и 8 см, а один из углов равен 120.
5 x 2  14 x  8  0,
6 x  5  0.
С3. Решите систему неравенств 
С4. В основании пирамиды MABCD лежит квадрат ABCD со стороной, равной 8 см.
Грани MBA и MBC перпендикулярны плоскости основания. Высота пирамиды
равна 6 см. Найдите площадь боковой поверхности пирамиды.
С5. Найдите наименьшее значение выражения 6 x  5 y  7  2 x  3 y  1 и укажите
пары значений переменных, при которых оно достигается.
С6. Найдите все положительные значения k, при которых прямая y  kx пересекает
в двух различных точках ломаную, заданную условиями:
если х  3
1,

у   2 х  5, если x  3
2 х  5, если x  3.
