Математика для участников школьных олимпиад. Решение

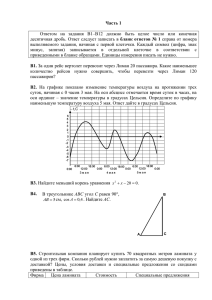
НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ
«АССОЦИАЦИЯ МОСКОВСКИХ ВУЗОВ»
РОССИЙСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
МЕДИЦИНСКИЙ УНИВЕРСИТЕТ ИМЕНИ Н.И. ПИРОГОВА
МИНИСТЕРСТВА ЗДРАВООХРАНЕНИЯ И СОЦИАЛЬНОГО РАЗВИТИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ МАТЕРИАЛ
МАТЕМАТИКА
ДЛЯ УЧАСТНИКОВ ШКОЛЬНЫХ ОЛИМПИАД
РЕШЕНИЕ ЗАДАНИЙ
ОЛИМПИАДНОГО УРОВНЯ
Москва 2011 г.
1
СОДЕРЖАНИЕ
ПОДХОДЫ К РЕШЕНИЮ ЗАДАНИЙ ОЛИМПИАД .................................. 5
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ........................ 18
ИЗДАНИЯ ДЛЯ ПОДГОТОВКИ К ОЛИМПИАДЕ..................................... 23
ИНФОРМАЦИОННЫЕ ИНТЕРНЕТ-РЕСУРСЫ ДЛЯ ПОДГОТОВКИ К
ОЛИМПИАДЕ ..................................................................................................... 23
2
Ключевые слова: задания олимпиадного уровня, решение, математика,
олимпиады школьников, литература для подготовки.
Объект
разработки
и
исследования:
содержательная
часть
общеобразовательного предмета математика для участников предметных
олимпиад школьников по биологии.
Цель работы: применение собственного многолетнего опыта проведения
олимпиад школьников по математике для развития творческого потенциала,
улучшения качества подготовки школьников по математике, повышения
конкурентоспособности школьников при продолжении образования медикобиологического профиля.
Методология проведения работы: анализ опыта проведения олимпиад по
общеобразовательному предмету математика в РНИМУ им. Н.И. Пирогова,
разработка
на
материала
для
основании
имеющихся
обучающихся
средних
данных
научно-образовательного
общеобразовательных
учебных
заведений, обладающего достаточной степенью информативности и творческим
компонентом,
разработка
заданий
для
самоподготовки
учащихся
и
абитуриентов, с возможностью использования в аудиторной работе со
школьниками.
Область применения: предлагаемый научно-образовательный материал
по математике адресован школьникам и абитуриентам, желающим улучшить
свою подготовку по математике, расширить область познаний в широком
спектре, а также готовящимся к участию в олимпиадах, сдаче ЕГЭ и
вступительных испытаний в вузах.
Степень внедрения: олимпиадные задания повышенного уровня,
представленные в научно-образовательном материале, и аналогичные успешно
применяются с 2008 года при проведении предметных олимпиад школьников в
РНИМУ им. Н.И. Пирогова, в т.ч. и входящих в ежегодный Перечень олимпиад
школьников. В олимпиадах участвовали обучающиеся общеобразовательных
3
учебных заведений московского региона, в т.ч. и учащиеся профильных
классов медико-биологического профиля.
4
ПОДХОДЫ К РЕШЕНИЮ ЗАДАНИЙ ОЛИМПИАД
Задача 1
Решить уравнение:
+
.
Решение:




cos  2 x    3cos  2 x    3
2
2




4 cos  2 x    3
2

3
 sin 2 x  
4
3
n
2 x   1 arcsin   n
4
 1
x
n
2
3 n
arcsin 
,nZ
4 2
Задача 2
9  5x 
Решить неравенство: 16  
 0
 x4 
.
2
Решение:
I способ
9  5x
 9  5x 
4

  16 
x4
 x4 
2


 x  4
 x  4


 9  5x
 9  5 x  4 x  16
 4 ;
 0;

x4
 x4

 9  5x
 9  5 x  4 x  16
0
 x  4  4 
x4

 x  4

9x  7
0

x

4

 x  25
 x  4  0
x    7 ; 25
 9

-4
-7/9
25
x
5
II способ
9  5x  
9  5x 

4
 x 
0
x  4 
x4 

4 x  16  9  5 x 4 x  16  9  5 x

0
x4
x4
 9 x  7   x  25  x  4 2
;

 x  4
-7/9
25
x
 9 x  7  x  25   0
Ответ:  7 9 ;25
Задача 3
Два автомобиля, двигаясь по кольцевой дороге с постоянными
скоростями в одном направлении, оказываются рядом через каждые 56 минут.
При движении с теми же скоростями в противоположных направлениях
автомобили встречаются через каждые 8 минут. За какое время проедет всю
кольцевую трассу каждый автомобиль?
Решение.
Пусть S – длина кольцевой дороги, t1 и t2 – время (в секундах)
прохождения кольцевой дороги первым и вторым автомобилями, тогда S и S
t1
t2
– их скорости. Предположим, что t1 < t2. Из условий задачи составляем
уравнения:
6
 S S 
    56  S
 t1 t2 
;



S
S
 
 t t   8  S
 1 2 
1 1 1
 t  t  56
1 2

1  1  1
 t1 t2 8
(1)
(2)
1   2  ;
 2 1 1 1 7 1
 t  56  8  56  7
1

 2  1  1
 t2 56 8
t1  14
t1  14


 2 1 7 ;  2 3 ;
 t  56  t  28
 2
2
t1=14
t1  14


56
t2  3
2
Ответ: t1=14 сек. t2  18 сек.
3
Задача 4
Доказать, что при любом целом n выражение 2n3+3n2+7n делится на 6.
Доказательство:
Имеем 2n3+3n2+7n= n3-n+ n3+3n2+2n+6n=n(n2-1)+n(n2+3n+2)+6n=
=(n-1)n(n+1)+n(n+1)(n+2)+6n
(n-1)n(n+1) и n(n+1)(n+2) – произведения 3х последовательных натуральных
чисел  каждое из этих выражений и слагаемое 6n делится на 6 как кратное 6.
Если все слагаемые делятся на 6, то и все выражения делятся на 6.
Задача 5
В арифметической прогрессии, разность которой отлична от нуля, сумма
первых 3n членов равна сумме следующих n членов. Найти отношение суммы
первых 2n членов к сумме следующих 2n членов.
Решение:
Пусть а – первый член арифметической прогрессии, d – ее разность.
Следовательно, сумма первых k членов этой прогрессии находится по
формуле Sk 
2a  d (k  1)
k
2
7
По условию S3n  S4n  S3n (1)
2S3n=S4n;
2a  d (3n  1)
2a  d  (4n  1)
 3n 
 4n
2
2
(2a  d (3n  1))3 n  (2a  d (4n  1))2 n
3  2a  3d (3n  1)  4a  2d  (4n  1)
2a  (8n  2  9n  3)d;
2a  (1  n)d
2
Подставим значение 2a в условие
S2 n
(2a  d (2n  1))2n
(2a  d (2n  1))
2a  d (2n  1) d (1  n)  d (2n  1) dn 1






S4 n  S2 n (2a  d (4n  1))4n  (2a  d (2n  1))2n 4a  2d (4n  1)  2a  d (2n  1) 2a  (6n  1) d d (1  n)  (6n  1) d 5dn 5
Ответ:
1
5
Задача 6
Касательная к графику функции y  3 x 2 такова, что абсцисса x точки
касания принадлежит отрезку
1 
 2 ;1 .
При каком значении x площадь
треугольника, ограниченного этой касательной, осью ОХ и прямой x = 2 будет
наименьшей. Чему равна эта наименьшая площадь.
SABC → max.
1
 AC  BC
2
yx=f(xk)+f'(xn)  (x–x0)
SABC=
y
B
A
1
2
x0
C
2
x
8
Пусть x0=k
y( x)  2 3  x 1 3
1 3
0
yx  x0  2 3  x
3
2
3  x0 2  2 x  2 x  2  x0
 ( x  x0 ) 
3
точка Ax  y=0
3  x0 2  2 x  2 x0  0
x
2 x0  3 x0 2
2
3  x0 2  2 x0  4
3
2
3 x0  2 x0  4 2 x0  3 x0 2 12 x0 2  10 x0  4
AC 


3
2
6
Cx  Bx  y (2) 
CB  By  y (2) 
3 x0 2  2 x0  4
3
1 12 x0 2  10 x0  4 3x0 2  2 x0  4 (6 x0 2  5 x0  4)(3x0 2  2 x0  4)
S 


2
6
3
18
S  S ( x0 )
1
S ( x0 )   ((12 x0  5)(3x0 2  2 x0  4)  (6 x0 2  5 x0  4)(6 x0  2))
18
Задача 7
Из точки М на плоскость α опущен перпендикуляр МН длины
3 и проведены
две наклонные, составляющие с перпендикуляром углы по 600 . Угол между
наклонными равен 1200 .
а) Найти расстояние между основаниями А и В наклонных.
б) На отрезке АВ как на катете в плоскости α построен прямоугольный
треугольник
1
3
АВС (угол А-прямой). Найти объем пирамиды МАВС, зная, что cos BMC   .
9
M
a)
1.
MH
 cos 60
AM
MH
3
AM 

2 3
cos 60 1 2
AMH :
3
H
B
A
2.
C
AMH  MHB  AM  MB  2 3
α
 1
AMH : AB  MA2  MB 2  2  MA  MB  cos120  12  12  2 12 12      2 42.
 2
1
3
б) cos BMC   . Найдем объем пирамиды.
т.к.
AH
 tg 60
MN
AH  3  3  3
AH  HB  AH  BH  6  точка A, B
и H – лежат на одной прямой  точка A, B, H и M лежат в одной плоскости
перпендикулярной плоскости α. И MAC  90 по теореме о трех
перпендикулярах.
Пусть AC  x , тогда
MC  MA2  AC 2  12  x 2
BC  AB 2  AC 2  36  x 2
по теореме косинусов
BC 2  MC 2  MB 2  2  MB  MC  cos BMC
 1
36  x 2  12  x 2  12  2 12  x 2  2 3    
 3
4
12  x 2  12  12  x 2  27  x  15
3
1
1
1
1
1
V   MH  S ABC   MH  AB  AC 
3  6 15  3 5
3
3
2
3
2
Ответ: a) 2 42
б) 3 5
Решить неравенство 2lg( x 1)  ( x  1)lg 2 .
2
10
О.Д.З: x2 1  0, x  1
т.к. по смыслу x 1  1 , x  1  0 и 2  1 , то
log 2 2lg( x
2
1)
 log 2 ( x  1) lg 2
lg( x  1)  lg( x  1)  lg 2  log 2 ( x  1)
lg( x  1)
lg 2
x 1  1
lg( x  1)  lg( x  1)  lg 2 
lg( x  1)  0
x2.
Ответ: x  2 .
Задача 8
Найти значения параметра a, при каждом из которых уравнение
x 2  5 x  a ( x  4) имеет ровно три различных корня.
Решение:
Введем функции y1  x 2  5 x и y2  a(4  x)
y1 – четна относительно OY и OX  график может быть получен симметриями
графика y=x2-5x.
Построим графики обеих функций в одной системе координат.
Графиком функции y2 является прямая.
y
-5
5
x
Графики функций y1 и y2 пересекаются ровно в трех точках либо когда
a=0, либо когда уравнение a(x+4)=5x–x2 имеет одинаковый корень,
расположенный в интервале (0;5), т.е.
x 2  (a  5)  x  4a  0 единственный корень  D=0
D  (a  5)2  16a
a  1
 a  25

при a=1
x1,2  
1 5
2
2
  0;5
a2-2a+25=0
x1,2  
b
2a
11
У нас b=a–5
a=1
 a=1
y
x
y2=a(x+4)
a<0
a( x  4)  5 x  x 2 – имеет единственный корень из интервала (–5;0)
D  a 2  14a  25
x 2  (5  a) x  4a  0
a1,2  7  24  0
a 2  14a  25  0
Ответ: (0;1)
Задача 9
Два ромба ABCD AMHK, имеющие общую вершину расположены так, что
стороны AB и AM образуют угол в 300. Известно, что углы при вершине A
обоих ромбов равны 600, площадь пресечения ромбов равна 5 3 , а площадь их
объединения равна 23 3 . Найти площадь каждого ромба.
I случай.
B
M
b
C
AH  AB
H
a
K
А
S ABCD 
D
a2 3
2
S AMHK 
Пусть стороны ромбов ABCD и AMHK
равны соответственно a и b.
Поскольку острые углы этих ромбов
содержат по 60º, то
b2 3
2
пересечение – это ΔAHK
объединение – ромб ABCD+ΔAMH  имеем
 a 2 3 b2 3

 23 3

 2
4
 2
b 3  5 3
 4
a4
b2 5
НО! AH должно быть  AB
12
ΔAKH по теореме косинусов AH  2 15  6  AH>AB – противоречие.
II случай.
H
30º 30º
E
B
M
C
K
30º
А
D
AB  AH  3AB
пересечение – четырехугольник ABEK
объединение – ABCD+ΔAMH+ΔBHE
из ΔAMH по теореме косинусов – AH  b 3 , тогда BH  b 3  a
BEH  90 , т.к. ABC  120 – это внешний угол ΔBHE
 EBH  60  S BHE
S AHK 
b
2
3


3b  a

2
3
8
SABEK = SAHK – SBEH
4


2
 2
2
3b  a
3
b
3
a
3



 23 3
 4
2
8

2
 b2 3
3b  a
3


5 3
8
 4



 a  4

 b  2

 a  2

 b  4
2
6
все подходит.
6
2
III случай.
H
C
B
K
M
13
А
D
AH  3AB
пересечение – ΔABC
объединение – AMHK+ΔACD
 b2 3 a 2 3

 23 3

 2
4
 2
a 3  5 3
 4
b6
a2 3
НО! AH  b 3  6 3  3a  6 5 – не удовлетворяет рассматриваемому случаю
S ABCD  16 3
S AMHK  12 3
или
S ABCD  12 3
S AMHK  16 3
Ответ:
S ABCD  12 3
S AMHK  16 3
Задача 10
Укажите простое натуральное число, которое не входит в область
определения функции
и при этом наименее удалено от
этой области.
;
;
;
<0,5
1,5
<0,5
17,5
x
Так как число должно быть простым, то ответ: 1
Задача 11
Вычислить cos α, если
и
14
т. к.
II четверти, то
Ответ:
Задача 12
Доказать, что точки А(-3;1), В(2;4), С(7;-1), D(2;-6) являются вершинами
квадрата. Найти длины сторон и длины диагоналей.
B
-3
A
C
-1
диагонали
взаимно ⊥
D
ABCD – квадрат.
Задача 13
Решить неравенство.
-
-4
x
-
+
+
-2 + -1 +
0
15
Ответ:
Задача 14
x – число сотен
y – число десяток
z – число единиц
Тогда 100x+10y+z – исходное число
100z+10y+x – после перестановки
Тогда 100x+10y+z=100 или 1
100z+10y+xИли
Или
z и х определяются подобным образом
z=6, x=2
Ответ: 216 и 612
Задача 15
Решить неравенство
ОДЗ:
Так как
всегда, то
Таким образом
Ответ:
Задача 16
В конусе осевое сечение проходит через образующие SA и SB. Найти
расстояние между А и серединой SB, если объём конуса равен 720 , а площадь
его осевого сечения равна 180.
16
S
H
A
O
B
Ответ: 19,5
17
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ
Задача 1
Найти длину промежутка, являющегося множеством решений неравенства
2x  3 2  4
.
Задача 2
2
Решить уравнение: 6 x  cos 7x  10  x .
Задача 3
Если двузначное число разделить на сумму его цифр, то в частном получится 9,
а в остатке 1. Если из квадрата суммы цифр этого числа вычесть произведение
его цифр, то в результате получится данное двузначное число. Найдите это
число.
Задача 4
Координаты вершин треугольника ABC : А(1;2); В(0;3); С  ;2  1 . При каких
значениях α угол ВАС прямой?

Решить неравенство:
Задача 5

log sin x x 2  8 x  23 
3
log 2 sin x
.
Задача 6


 
tg      2  3    ;  

 2 .
Вычислить sin  , если  4
,
Задача 7
Основание пирамиды – квадрат АВСD со стороной равной a . Боковое ребро
AM перпендикулярно плоскости основания пирамиды и вдвое больше ребра
основания. Найти радиус сферы, описанный около этой пирамиды.
Задача 8
Семь грибников собрали вместе 100 грибов, причем все семеро собрали разное
число грибов. Докажите, что есть 3 грибника, которые вместе собрали не
меньше 50 грибов.
Задача 9
Покажите, что если
3
z  a  a 2  b3 
3
a 2  b3  a ,
то
18
z 3  3bz  2a  0 .
Задача 10
Найти все корни уравнения
sin x  tg 2 x  3 (sin x  3tg 2 x )  3 3 ,
2  log 1 x  0
удовлетворяющие неравенству
2
.
Задача 11
Решить неравенство
log 1 x  log 3 x  1
2
.
Задача 12
Пешеход шел вдоль трамвайной линии. Через каждые 4 минуты он встречал
вагон трамвая, а через каждые 12 минут его обгонял вагон трамвая. Пешеход и
трамваи двигались равномерно. Через сколько минут следуют друг за другом
вагоны трамвая?
Задача 13
В треугольной пирамиде боковые ребра равны, а в основании ее лежит
прямоугольный треугольник, высота которого опущенная из вершины прямого
угла, равна h. Двугранные углы, образованные гранями пирамиды,
пересекающимися по катетам основания, равны  и . Найдите объем
пирамиды.
Задача 14
Найти решение уравнения
1  x2  a  x
для всех значений параметра a.
Задача 15
Найдите два трехзначных числа, сумма которых кратна 504, а частное кратно 6.
Задача 16
Когда обезьяна несла три одинаковых кокосовых ореха на вершину
многоэтажного дерева, один орех упал с одиннадцатого этажа и разбился.
Обезьяна хочет определить самый высокий этаж, при падении с которого
кокосовые орехи не разбиваются. Она может уронить орех с любого этажа и
подобрать его, если он цел. Докажите, что ей хватит четырех испытаний (с
двумя орехами).
Задача 17
Решить уравнение
.
19
Задача 18
Решить неравенство
.
Задача 19
Два автомобиля, двигаясь по кольцевой дороге с постоянными скоростями в
одном направлении, оказываются рядом через каждые 56 минут. При
движении с теми же скоростями в противоположных направлениях
автомобили встречаются через каждые 8 минут. За какое время проедет всю
кольцевую трассу каждый автомобиль?
Задача 20
Доказать, что при любом целом выражение
делится на 6.
Задача 21
В арифметической прогрессии, разность которой отлична от нуля, сумма
первых
членов равна сумме следующих членов. Найти отношение
суммы первых
членов к сумме следующих
членов.
Задача 22
Касательная к графику функции
такова, что абсцисса точки
касания принадлежит отрезку
. При каком значении площадь
треугольника, ограниченного этой касательной, осью ОХ и прямой
будет наименьшей. Чему равна эта наименьшая площадь.
Задача 23
Из точки М на плоскость α опущен перпендикуляр МН длины
и
проведены две наклонные, составляющие с перпендикуляром углы по 600 .
Угол между наклонными равен 1200 .
а) Найти расстояние между основаниями А и В наклонных.
б) На отрезке АВ как на катете в плоскости α построен прямоугольный
треугольник АВС (угол А-прямой). Найти объем пирамиды МАВС, зная, что
.
Решить неравенство
Задача 24
.
Задача 25
Найти все значения параметра , при каждом из которых уравнение
имеет ровно три различных корня.
20
Задача 26
Два ромба ABCD AMHK, имеющие общую вершину расположены так, что
стороны AB и AM образуют угол в 300. Известно, что углы при вершине A
обоих ромбов равны 600, площадь пресечения ромбов равна
, а площадь их
объединения равна 23 . Найти площадь каждого ромба.
Задача 27
Доказать равенство
4
1

4
3  9  4 27  3

4

3  1 4 27
6
.
Задача 28
Решить неравенство
Решить уравнение
2
1
2 x3
.


Задача 29


log 2 x  x  1  log 2 x 2  x  1  log 2 1  2 x  .
2
Задача 30
2
Решить уравнение cos x  cos 2 x  cos 3x .
2
2
Задача 31
Найти число решений уравнения
2 x 1  21 x  1  4 x  x 2
Задача 32
Найти все значения параметра а, при которых уравнение
a  6 x  x2  8  3  1  2ax  a 2  x2 имеет ровно одно решение.
Задача 33
Дана правильная треугольная пирамида SAB. Точка S– вершина пирамиды. AB
= 1, AS = 2, BM - медиана треугольника SAB. Найти длину отрезка DM
Задача 34
Абитуриенты сдавали экзамены в течение трех дней в одних и тех же
аудиториях. Число экзаменовавшихся в каждый день абитуриентов в каждой
аудитории было равным числу аудиторий. Если бы экзамены проводились в
другом корпусе, то их можно было бы провести за два дня, используя каждый
день одни и те же аудитории, причем каждый день в каждой аудитории
абитуриентов удалось бы рассадить по рядам так, что число рядов, а также
число людей в ряду было бы равным числу используемых аудиторий. Найти
минимальное возможное число абитуриентов, которое могло бы быть
проэкзаменовано при этих условиях.
21
Задача 35
Решить уравнение
.
Задача 36
.
Решить неравенство
Задача 37
Собака, находясь в точке А, погналась за лисицей, которая была на расстоянии
30м от собаки в точке В. Скачок собаки равен 2м, скачок лисицы – 1м. Собака
делает два скачка в то время, когда лисица делает три скачка. На каком
расстоянии от А собака догонит лисицу?
Задача 38
Доказать равенство
.
Задача 39
Сумма первых 5 членов геометрической прогрессии равна ее первому члену,
умноженному на 5, а сумма первых 15 членов равна 100. Найти сумму первого,
шестого и одиннадцатого членов этой прогрессии.
Задача 40
Даны две концентрические окружности с радиусами 2см , 4см и центром в
точке O. Точки P и Q лежат на окружности большего радиуса. Угол POQ=x,где
x
.
P
O
Q
1). Найти площадь заштрихованной фигуры.
2). Найти x при котором площадь будет принимать наибольшее значение.
Задача 41
Дан куб EFGHE1F1G1H1 с длиной ребра, равной 2. На ребрах EH и HH1 взяты
точки A и B такие, что EA/AH=2, HB/BH1 = . Через точки A1B1G1 проведена
плоскость. Найти расстояние от точки Е до этой плоскости.
Задача 42
Решить неравенство
.
22
Для каждого
Задача 43
найти наибольшее значение величины
.
при условии
Задача 44
Две окружности с центрами A и B радиусов 2 и 1 соответственно касаются друг
друга. Точка C лежит на прямой, касающейся каждой из окружностей и
находится на расстоянии
от середины отрезка AB. Найти площадь S
треугольника ABC, если известно, что S>2.
ИЗДАНИЯ ДЛЯ ПОДГОТОВКИ К ОЛИМПИАДЕ
1. В.И. Арнольд. Задачи для детей от 5 до 15 лет.
2. А.Я. Канель-Бенов, А.К. Ковальджи. Как решают нестандартные задачи.
3. А.Г. Цыпкин, А.И. Пинский. Справочное пособие по математике с
методами решения задач для поступающих в ВУЗы.
4. И.Н. Сергеев, С.Н. Олехник, С.Б. Гашков. Примени математику.
5. И.Н. Сергеев. Математика. Задачи с ответами и решениями.
ИНФОРМАЦИОННЫЕ ИНТЕРНЕТ-РЕСУРСЫ ДЛЯ
ПОДГОТОВКИ К ОЛИМПИАДЕ
1.
2.
3.
4.
5.
http://www.math.ru
http://www.mccme.ru
http://www.allmath.ru
http://tasks.ceemat.ru
http://www.shevkin.ru
23