ω ω μω × = Δ t
реклама

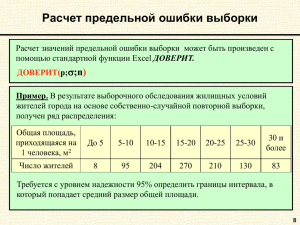
При бесповторном собственно случайном отборе общее количество статистических единиц в генеральной совокупности в процессе формирования выборки меняется, уменьшаясь каждый раз на единицу, попавшую в выборку, поскольку отобранные единицы в генеральную совокупность не возвращаются. Таким образом, вероятность попадания отдельных единиц в выборку при бесповторном случайном отборе также меняется (для оставшихся единиц она возрастает). В целом вероятность попадания любой статистической единицы в выборку при бесповторном отборе может быть определена как 1 − n . На эту величину должна быть N скорректирована и средняя ошибка выборки при бесповторном отборе. Таким образом, расчетные формулы средней ошибки выборки при бесповторном отборе принимают вид: • для средней количественного признака μ ~x = • μω = S ~x2 n × (1 − ) ; n N для доли альтернативного признака ω ×(1−ω) n n ×(1− ) . N На практике при применении выборочного метода определяются пределы, за которые не выйдет величина конкретной ошибки выборочного исследования. Величина пределов конкретной ошибки определяется степенью вероятности, с которой измеряется ошибка выборки. Ошибка выборки, исчисленная с заданной степенью вероятности, называется предельной ошибкой выборки. Предельная ошибка выборки является максимально возможной при данной вероятности ошибкой. Это означает, что с заданной вероятностью гарантируется, что ошибка любой выборки не превысит предельную ошибку. Такая вероятность называется доверительной. Предельная ошибка Δ выборки рассчитывается по формуле: Δα~ = t × μα~ ; где t – коэффициент доверия, значения которого определяются доверительной вероятностью Р(t ) . Значения коэффициента доверия t задаются в таблицах нормального распределения вероятностей. Чаще всего используются следующие сочетания: 157 t 1 1,5 2,0 2,5 3,0 3,5 Р(t ) 0,683 0,866 0,954 0,988 0,997 0,999 Так, если t = 1, то с вероятностью 0,683 можно утверждать, что расхождение между выборочными характеристиками и параметрами генеральной совокупности не превысит одной средней ошибки. Предельные ошибки выборки Δ для разных параметров при разных методах отбора статистических единиц рассчитываются по формулам, приведенным в таблице 8.2. Таблица 8.2. Предельные ошибки выборки Метод отбора Повторный Бесповторный Предельные ошибки выборки Для средней Для доли Δ ~ x = t× S ~x2 n S~x2 n Δ~x = t × × (1− ) n N Δω = t × Δω = t × ω × (1 − ω ) n ω × (1 − ω ) n × (1 − n ) N Зная величину предельной ошибки выборки, можно рассчитать интервалы для характеристик генеральной совокупности: Доверительный интервал для генеральной средней равен (~ x ± Δ~ x ) ; для генеральной доли - (ω ± Δω ) . Рассмотрим нахождение средних и предельных ошибок выборок, определение доверительных интервалов для средней и доли на следующем примере: При оценке спроса на товар А. было проведено пятипроцентное бесповторное обследование регионального рынка. При этом было выяснено, что в 90 из 100 обследованных семей данный товар потребляется. В среднем каждая из обследованных семей потребляла 5 единиц товара ( ~x = 5) при стандартном отклонении 0,5 единицы (S=0,5 ед.). С вероятностью p=0,954 установить долю семей, потребляющих данный товар и среднее его потребление (спрос). 158