f`(x) - Кемеровский государственный университет

ГОУ ВПО «КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
КАФЕДРА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ФУНКЦИИ
в ЕГЭ по математике
Кемерово 2010
Функции в ЕГЭ по математике/ ГОУ ВПО «Кемеровский государственный университет»; сост. И.Л. Трель, И. В. Казаченко. – Кемерово, 2010. – 34с.
Учебное пособие предназначено для подготовки выпускников общеобразовательных учебных заведений к ЕГЭ по математике, а
также для учащихся старших классов, желающих систематизировать свои знания по предмету, учителей школ и подготовительных
отделений ВУЗов. В пособии рассмотрены основные положения
теории «Функции и их свойства» и наряду с теоретическим материалом представлен комплект заданий как с решениями, так и для
самостоятельной подготовки.
Утверждено методической комиссией математического факультета
Рассмотрено на заседании
кафедры дифференциальных
уравнений
«
«
»
2010г.
Председатель метод. комиссии
Л. Н. Фомина
2010 г.
»
Зав. кафедрой
Н.А. Кучер
Содержание
Введение
4
§ 1. Понятие функции и способы ее задания
4
§ 2. Область определения и множество значений функции
6
§ 3. Ограниченность функции
13
§ 4. Четность и нечетность функции
15
§ 5. Периодичность функции
18
§ 6. Монотонность функции
23
§ 7. Точки экстремума. Наибольшее и наименьшее значе-
27
ния функции
Приложение 1. Производная
33
Приложение 2. Графики элементарных функций
34
33
Введение
Понятие функции часто встречается в школьном курсе математики и хорошо знакомо учащимся. Умение находить область определения и множество значений, нули функции, промежутки знакопостоянства и монотонности, точки экстремума – залог успешного решения задач единого экзамена. Можно выделить два обобщенных умения, связанных с исследованием свойств функций:
1) уметь «читать» график функции и переводить его свойства с
графического языка на алгебраический и наоборот;
2) уметь работать с формулой, задающей функцию, обосновывая
или проверяя наличие указанных свойств, что связывает задачи
данного блока и с другими темами школьного курса (решение
уравнений и неравенств, вычисление производных и др.)
Для абитуриентов данное пособие предоставляет возможность
для тренировки и овладения необходимыми для успешной сдачи
ЕГЭ по математике умениями и навыками, тем более что многие из
предлагаемых задач взяты из реальных экзаменационных материалов прошлых лет.
§ 1. Понятие функции и способы ее задания
Самым общим в математике является следующее определение
функции. Говорят, что задана функция, если
1) задано множество Х, называемое областью определения
функции;
2) задано множество Y, называемое областью значений функции;
3) указано правило (закон) f, с помощью которого каждому
элементу х из Х, ставится в соответствие единственный
элемент y из Y, то есть
f
x a y.
В этом случае x называется независимой переменной или аргументом, а y – зависимой переменной, или функцией.
Чаще всего функции задаются в виде формулы
y=f(x).
44
Это так называемый аналитический способ задания функции, когда
используют некоторый запас изученных и специально обозначенных функций и алгебраические действия. Например, y=2x+5,
y=sin x, y=1-ln x.
Также используется табличный способ задания функции. Примерами табличного задания функции являются таблица квадратов,
таблица кубов, таблица значений синусов, косинусов и т.д. При
этом способе приводится таблица, указывающая значения функции
для имеющихся в таблице значений аргумента:
x
y
x2
y2
x1
y1
x3
y3
x4
y4
Важное значение для практики имеет графический способ
задания функции. Графиком функции y=f(x) называется множество
точек координатной плоскости, абсциссы которых равны
значениям аргумента, а ординаты – соответствующим значениям
функции. Задавая функцию графиком, нужно иметь в виду, что не
всякая линия является графиком функции. Если на кривой найдутся
хотя бы две точки, имеющие различные ординаты при одинаковых
абсциссах, то эта кривая не является графиком функции, так как в
этом случае нарушается условие единственности.
Рис 1. Кривая, не являющаяся
графиком функции
Рис. 2. Кривая, являющаяся
графиком функции
55
§ 2. Область определения и
множество значений функции
Областью определения D(y) функции y=f(x) называется множество всех значений аргумента х, для которых выражение f(x) определено (имеет смысл). Области определения основных элементарных функций:
1
D  = (−∞;0) ∪ (0;+∞ );
 x
D (log a x ) = (0;+∞ ),
( )
D a x = ( −∞;+∞ ),
a > 0, a ≠ 1;
a > 0;
π


D (tg x ) =  x ∈ R : x ≠ + π k , k ∈ Z ;
2


D (ctg x ) = {x ∈ R : x ≠ π + π k , k ∈ Z };
D (arctg x ) = D ( arcctg x) = ( −∞;+∞ );
D (sin x ) = D (cos x ) = ( −∞;+∞ );
D (arccos x ) = D (arcsin x) = [ −1;1];
D
( x ) = [0;+∞),
2n
n ∈ N;
областью определения любого многочлена, а также корня нечетной
степени является вся числовая прямая.
Множеством (областью) значений E(y) функции y=f(x) называется множество всех таких чисел y0, для каждого из которых найдется число x0 такое, что: f(x0)=y0.
Области значений основных элементарных функций:
1
E   = (−∞;0) ∪ (0;+∞ );
x
E
E (log
a
( x ) = [0;+∞),
2n
x ) = ( −∞ ; +∞ ),
66
n ∈ N;
a > 0 , a ≠ 1;
( )
E a x = (0;+∞ ),
a > 0;
E (sin x) = E (cos x) = [ −1;1];
E (tg x) = E (ctg x) = ( −∞;+∞ );
E (arcsin x ) = [ −π / 2; π / 2],
E (arccos x ) = [0; π ];
E (arctg x ) = ( −π / 2; π / 2),
E ( arcctg x) = (0; π );
( )
E (x
) = (−∞;+∞),
E x 2 n = [0;+∞ ),
2 n +1
n ∈ N;
n ∈ N.
Пример 1. Множество значений функции, график которой изображен на рисунке 3, есть отрезок [-4; 3], а область определения –
интервал [-3; 7).
Рис. 3
Пример 2. Область определения и множество значений функции y = x3 + 1 есть вся числовая прямая, то есть D(y)=E(y)=(-∞; +∞ ).
Пример 3. Областью определения функции y = x − 5 является
множество D(y)=[5; +∞), так как иначе под корнем будет отрицательное число, а E(y)=[0,+∞)
sin 2 x
Пример 4. Для функции y =
область определения функx−4
ции: x ≠ 4 , область значений – промежуток [0;+∞).
77
Пример 5. Найдем область определения функции y=f(x)+g(x),
где f ( x ) =
x −1
и g ( x) = 5 − x 2 .
x−2
Первое слагаемое f(х) определено при выполнении двух условий:
1) подкоренное выражение неотрицательно,
2) знаменатель не обращается в нуль.
Первое условие означает, что x ≥ 1 , второе x ≠ 2 . Таким образом,
D(f)=[1,2)∪ (2; ∞) .
Функция g(x) определена при 5 − x 2 ≥ 0 , то есть при − 5 ≤ x ≤ 5 .
Область определения функции у=f(х)+g(х) представляет собой
пересечение областей определения функций f(х) и g(х). Следовательно, D(y)=[1, 2)∪(2, 5 ].
Пример 6. Найдем область определения функции
f(x)=log0,5(2x-x2).
Так как логарифм определен только для положительных выражений, получим: 2х - х2 > 0 или х(х - 2) < 0, а значит х∈(0;2). Таким
образом, D(f)=(0;2).
Пример 7. Найдем сумму всех целых чисел, входящих в область определения функции y=ln(x-2|x-3|).
Так как подлогарифмическое выражение должно быть положительно, то x-2|x-3|>0, или 2|x-3|<x. Полученное неравенство равносильно совокупности двух систем:
x < 3
x ≥ 3
или 

2( x − 3) < x
2(3 − x) < x
⇔
x ≥ 3

x < 6
или
x < 3

.
x > 2
Целые числа, входящие в решение первой системы: 3, 4, 5; в решении второй системы целых чисел нет. Тогда сумма целых чисел,
входящих в область определения заданной функции: 3 + 4 + 5 = 12.
Пример 8. Для функции y=2x+5 D(y)=(-∞; +∞), а E(y)=(5; +∞)
Пример 9. Для функции y=3+lnx D(y)=(0,+∞), а E(y)=(-∞; +∞).
Пример 10. Определим наибольшее целое значение функции
y = 2,5 8 cos2 2 x − 5 cos 4 x + 7 .
Преобразуем выражение, стоящее под знаком корня:
88
8 cos 2 2 x − 5 cos 4 x + 7 = 8 cos 2 2 x − 5(2 cos 2 2 x − 1) + 7 = 12 − 2 cos 2 2 x.
Оценим получившееся выражение: так как 0≤cos22x≤1, то
-2≤-2cos22x≤0 и 10≤12-2cos22x≤12. Значит, наибольшее значение
данной функции достигается, если подкоренное выражение равно
12, то есть yнаиб=2,5√12=5√3.Так как 5√3≈8,5, то наибольшее целое
значение функции равно 8.
Задания для самостоятельного решения
1. Укажите натуральное число, не принадлежащее области
определения функции:
а)
Ответ: 64
Ответ: 81
б)
2. Укажите целое число, принадлежащее области определения
функции y=4x-lg(1-4x2)
Ответ: 0
3. Найдите наибольшее целое число, принадлежащее области
определения функции:
а) y = 4 − x
-x/7
б) y=(3
Ответ: 4
Ответ: 0
1/2
-1)
Ответ: 14
в) y=ln(60-|3+4x|)
Ответ: 13
г) y=ln(|3x-10|-31)
4. Найдите наименьшее целое число, принадлежащее области
определения функции
Ответ: -14
а)
Ответ:6
б)
99
Ответ: 0
в)
г)
Ответ: 1
Ответ: -7
д) y=ln(30-|8-3x|)
Ответ: 5
е) y=log2(3x-12)
ж) y=log5(0,21-2x-5)
Ответ: 11
з) y=arcsin(3-x2)
Ответ: -2
и) y=arccos(5-x)
Ответ: 4
5. Найдите количество целых чисел, входящих в область
определения функции:
Ответ: 1
а)
Ответ:12
б)
в)
Ответ: 5
г) y=arccos(2x-5)
Ответ:2
6. Найдите количество целых чисел, не принадлежащих области
определения функции:
Ответ: 1
а)
2
б) y=log0,6(x -4x)
Ответ:5
в) y=ln(|3-5x|-41)
Ответ: 8
г)
Ответ: 10
110
7. Найдите сумму всех целых чисел, принадлежащих области
определения функции:
Ответ: 9
а)
Ответ:-15
б)
в)
Ответ: 9
г) y=lg(5x-x2)
Ответ: 10
8. Найдите сумму всех целых чисел, не принадлежащих области
определения функции
Ответ: -3
9. Найдите наименьшее целое число, принадлежащее множеству
значений функции
а) y=4sin x
Ответ: -4
б) y=-3cos(2x)
Ответ: -3
в) y=5sin(x-4)
Ответ:-5
г) y=4cos25x
Ответ: 0
д) y=3cos(6x)-1
Ответ: -4
е) y=sin3 cos x –cos3 sin x
Ответ: -1
ж) y=5-2sin x
Ответ: 3
з) y=2+cos2(7x)
Ответ: 2
и) y=4+3sin4 x
Ответ: 4
к) y=2sin2x-3cos2x-1
Ответ: -4
л) y=3x+10
Ответ:11
м) y=4 53x-1
Ответ:0
н) y=7,5+lg2x
Ответ: 8
Ответ: -8
о) y=4arcsin(4x)-2
111
п) y=2tg26x-3
Ответ: -3
р) y=2-6arctg 5x
Ответ: -7
с) y=2+arccos2x
Ответ: 2
т) y=4-3arcsinx
Ответ: 0
у) y=sin x cos x
Ответ: 0
10. Найдите наибольшее целое число, принадлежащее множеству
значений функции:
а) y=-3sin(1-x)
Ответ: 3
Ответ: 5
б) y=5cos(3x)
Ответ: 1
2
в) y=2sin (x-4)-1
Ответ: 1
г) y=cos25x-sin25x
Ответ:1
д) y=cosx sin 3x+sinx cos 3x
Ответ: 2
е) y=2-5cos4 x
Ответ: 6
ж) y=2-3sin2x+4cos2x
Ответ: 6
з)
Ответ: 1
и)
Ответ: -4
x
к) y=-0,5 -7
л) y=1-4 53x
Ответ: 0
м) y=4-ln6x
Ответ: 4
11. Найдите количество целых чисел, принадлежащих множеству
значений функции:
а) y=6cos(2x)
Ответ:13
2
Ответ: 7
б) y=3sin (x/2)-2
Ответ: 13
в) y=4arccos(5x)+1
112
г) y=(2arctg x-π)/π
Ответ: 1
§ 3. Ограниченность функции
Функция y=f(x), определенная на множестве X, называется
ограниченной сверху, если множество её значений ограниченно
сверху. Иначе говоря, функция f ограничена сверху, если
существует такая постоянная М, что для каждого x ∈ X
выполняется неравенство f ( x) ≤ M .
Функция y=f(x), определенная на множестве Х, называется
ограниченной снизу, если множество её значений ограниченно
снизу, то есть если существует такая постоянная М, что для
каждого x ∈ X выполняется неравенство f ( x) ≥ M . Например,
таковыми являются показательные функции, функции y=x2n, y=√x.
Функция f(x), определенная на множестве Х, называется
ограниченной, если множество её значений ограниченно как сверху,
так и снизу. Примерами функций, ограниченных на всей числовой
прямой, являются функции y=sin x, y=cos x, y=arccos x, y=arcsin x,
y=arctg x, y=arcctg x.
При решении уравнений и неравенств свойство ограниченности функций часто играет определяющую роль. Например,
а) если для всех х из некоторого множества Х справедливы неравенства f(x)>M и g(x)<M, где М – некоторое число, то на множестве
Х уравнение f(x)=g(x) и неравенство f(x)<g(x) решений не имеют;
б) если для всех х из некоторого множества Х справедливы неравенства f(x)≥ M и g(x)≤M, где М – некоторое число, то на множестве
 f ( x) = M
Х уравнение f(x)=g(x) равносильно системе 
.
g
(
x
)
=
M

Пример 1. Решим уравнение: 2sin x=5+x2010.
При всех действительных х имеем 2sin x≤ 2, а 5+х2010≥5. Поскольку для любого х левая часть уравнения не превосходит двойки, а правая часть всегда не меньше пяти, то данное уравнение не
имеет решений.
Пример 2. Решим уравнение: cos4(2sin x)=1+5lg2(x2+x+1).
113
Функции, записанные в левой и правой частях уравнения, определены при всех действительных значениях х. Кроме того, для
любых х верно:
cos4(2sin x)≤1, 1+5lg2(x2+x+1)≥1.
Следовательно, данное уравнение равносильно системе уравнений
cos 4 (sin x) = 1
.

1 + 5 lg 2 ( x 2 + x + 1) = 1
Решения второго уравнения системы есть х=0 и х=-1. Из этих значений первому уравнению удовлетворяет только х=0, которое, следовательно, является единственным решением исходного уравнения.
Задания для самостоятельного решения
1. Найдите наибольшее целое число, принадлежащее
значений функции
2. Укажите сумму всех целых чисел, принадлежащих
значений функции
а)
множеству
Ответ: 2
множеству
Ответ: 1
Ответ: 1
б)
3. Решите уравнение:
а) (x2+2x+1)4+(2x-1)2=0
Ответ:∅
2
Ответ: 3
б) |3-x|+2|ln(x -4x+4)|=0
Ответ: 2πm, -π/2+2πk
в) cos5x+sin7x=1
Ответ: 3π/2+2πk
г) 3cos22x-2sin3x=5
Ответ: π+2πk
д) cos53x+cos117x= -2
е) x20=logπcos4x
Ответ: 0
ж) 5|x|=|cos x|
Ответ: 0
з) 4sin πx=4x2-4x+5
Ответ: 1/2
и) sin4x-cos4x= -1-x6
Ответ: 0
114
Ответ: π/2+2πk
к) sin x cos 4x=1
л) 2-|x-2|log2(4x-x2-2)=1
Ответ: 2
§ 4. Четность и нечетность функции
Функция y=f(x) называется чётной, если для любого x из D(f)
число –х также принадлежит D(f) и при этом справедливо равенство: f(-x)=f(x).Из числа элементарных функций четными являются
следующие: y=cos x, y=|x|, y=x2n, n∈N.
Функция y=f(x) называется нечётной, если для любого x из D(f)
число –х также принадлежит D(f) и при этом справедливо равенство: f(-x)=-f(x).Из числа элементарных нечетными являются функции
y=sin x, y=tgx, y=ctg x, y=1/x, y=x2n+1, n∈N.
Функция, не являющаяся ни четной, ни нечетной, называется
функцией общего вида.
Замечание. Область определения четных и нечетных функций
является симметричной относительно точки 0.
Четность или нечетность функции весьма существенно сказывается на форме графика этой функции.
График четной функции симметричен относительно оси Оу:
Рис.4 График четной функции
График нечетной функции симметричен относительно начала
координат:
115
Рис.5 График нечетной функции
Справедливы следующие утверждения:
1) если функции f и g четные, то h(x)=f(x)±g(x) и p(x)=f(x)g(x) –
четные;
2) если функции f и g нечетные, то h(x)=f(x)±g(x) – нечетные, а
p(x)=f(x)g(x) – четная;
3) если одна из функций f и g – четная, а другая – нечетная, то
p(x)=f(x)g(x) – нечетная.
Пример 1. Какие из функций обладают свойством четности:
а) f(x)=5x-5-x;
б) f(x)=cos(x-7)cos(7+x)?
Каждая из заданных функций определена на всей числовой
прямой. Вычислим f(-x):
а) f(-x)=5-x-5x=-f(x) – функция нечетная;
б) f(-x)=cos(-x-7)cos(7-x)=cos(x+7)cos(x-7)=f(x) – функция чётная.
Пример 2. Найдем значение функции y(х)=f(x)·g(-x)-f(-x) в точке х0, если известно, что функция f чётная, g – нечётная, f(х0) = -3,
g(х0) = -2.
Так как функция y = f(x) чётная, то f(-x) = f(x), а так как функция g(x) нечётная, то g(-x) = -g(x). Преобразуем данную функцию:
y(х) = f(x) · g(-x) - f(-x) = f(x) · (-g(x)) - f(x) = - f(x) · g(x) - f(x).
Тогда при х= х0 получим:
y(х0) = - f(х0) · g(х0) - f(х0) = -(-3) · (-2) - (-3) = -6 + 3 = -3.
Пример 3. Чётная функция y = f(x) определена на всей числовой прямой. Для функции g ( x) = 2,1 +
f ( x − 9,5)
вычислим
x − 9,5
сумму g(9)+g(10).
g (9) = 2,1 +
f (9 − 9, 5)
f (−0,5)
f (10 − 9,5)
f (0,5)
g (10) = 2,1 +
= 2,1 +
= 2,1 +
,
10 − 9,5
0,5
9 − 9, 5
−0, 5
116
Так как функция f по условию является чётной, то f(-0,5) = f(0,5).
f (0,5)
f (0,5)
Тогда g (9) + g (10) = 2,1 + −0,5 + 2,1 + 0,5 = 2,1 + 2,1 = 4, 2
Пример 4. При каких значениях параметра а функция
f ( x) = 12 − x 2 − 4 x + 2 36 − x 2 + 16 x − 3 x 2 − 4 + ax
является четной?
Найдем область определения заданной функции:
12 − x 2 − 4 x ≥ 0

2
36 − x + 16 x ≥ 0
 2
x − 4 ≥ 0
⇔
( x + 6)( x − 2) ≤ 0

( x − 18)( x + 2) ≤ 0
( x − 2)( x + 2) ≥ 0

⇔
х∈{-2,2}.
Оказалось, что область определения функции состоит из двух симметричных относительно начала координат точек. Для четности
функции нужно, чтобы значения функции в этих точках были равными: f(2)=f(-2), а значит 4-2a=16+2a, откуда а=-3.
Задания для самостоятельного решения
в точке х0,
1. Найдите значение функции
если функция f – четная, g – нечетная, f(х0)=1, g(х0)=-3
Ответ: -0,4
2. Найдите значение функции y(x)=f(x)g(-x)+2f(-x) в точке х0, если
известно, что функция f – четная, функция g – нечетная, f(х0)=2,
g(х0)=-3
Ответ: 10
3. Нечетная функция y=f(x) определена на всей числовой прямой.
Для
функции
g(x)=2,3+f(x-9)
вычислите
сумму
g(6)+g(8)+g(10)+g(12).
Ответ: 9,2
4. Четная функция y=f(x) определена на всей числовой прямой. Для
функции
вычислите сумму g(3)+g(4).
Ответ: 7,6
5. Четная функция y=f(x) определена на всей числовой прямой. Для
всякого неотрицательного значения переменной x значение этой
функции совпадает со значением функции g(x)=(x-1)(x-3)(x+7).
при x=-3. Ответ: -1
Найдите значение функции
117
6. Четная функция y=f(x) определена на всей числовой прямой. Для
всякого неотрицательного значения переменной x значение этой
функции совпадает со значением функции g(x)=(x+1)(x+3)(x-7).
Найдите
значение
функции
при
x=-3.
Ответ: 1
7. Нечетная функция y=f(x) определена на всей числовой прямой.
Для каждого неотрицательного значения переменной х значение
этой функции совпадает со значением функции g(x)=x(2x+1)(x2-5x+6).
Сколько
Ответ: 5
корней
имеет
уравнение
f(x)=0?
8. При каких значениях параметров а и b функция
f ( x ) = ax + 3 + x + b является четной?
Ответ: a=-1, b=3.
§ 5. Периодичность функции
Функция у=f(х) называется периодической с периодом Т, если
для каждого х из D(f) числа х+Т, x-T также принадлежат D(f) и при
этом справедливо f(x+Т)=f(x)=f(x-T).
Наименьшее из положительных чисел Т называется основным
периодом функции. Часто основной период функции называют
просто ее периодом.
Замечание 1. Область определения периодической функции
является неограниченной как в положительном, так и в отрицательном направлении оси Ох, при этом значения функции повторяются
через каждые Т единиц в обоих направлениях оси Ох.
Замечание 2. Если функция y=f(x) периодична с периодом Т,
то равенство f(х+пТ)=f(х) справедливо при любом целом n.
Функции y=sin x, y=cos x имеют период 2π, а функции y=tg x,
y=ctg x периодичны с периодом π. Среди остальных элементарных
функций периодических нет.
Для построения графика периодической функции достаточно
построить его на любом отрезке длиной в период, тогда весь гра-
118
фик получится сдвигом построенной части вправо и влево на целое
число периодов:
Рис. 6. График периодической функции
Пример 1. Функция y=f(x) определена на всей числовой прямой
и является периодической с периодом 6. При -2≤x<4 она задается
формулой f(x)=|x-2|-3. Найдем значение выражения 4f(11)-2f(-15).
Вычислим значения функции в заданных точках:
f(11)=f(11-2⋅6)=f(-1)=|-1-2|-3=3-3=0;
f(-15) = f(-15 + 3⋅6) =f(3)=|3 – 2| - 3=1 – 3=-2.
Тогда 4f(11)-2f(-15)=4⋅0-2⋅(-2)=4
Пример 2. Функция y = f(x) определена на всей числовой прямой и является чётной периодической функцией с периодом, равным шести. На отрезке [0,3] функция задана формулой f(x)=x2-2x-2.
Определим количество нулей этой функции на отрезке [-5, 4].
Учтём
сначала,
что
функция
чётная
и
построим
её график на отрезке [-3 , 3]:
.
Теперь воспользуемся периодичностью функции:
.
119
На отрезке [-5 , 4] четыре точки пересечения с осью Oх.
Пример 3. Найдем значения параметра а, при которых период
функции y=sin((a2+6a+1)x) равен π/4.
Заметим, что период функции y=sin kx при k≠0 равен не 2π/k, а
2π/|k|. Итак, период заданной функции равен 2π/|a2+6a+1|. Приравнивая эту величину к заданному периоду π/4, получаем
|a2+6a+1|=8.
Отсюда а удовлетворяет условиям a2+6a+1=8 и a2+6a+1= -8, то
есть принимает значения 1, -7 и -3.
Пример 4. Найдем период функции y=3cos3x+2cos 4x.
Пусть Т – основной период функции. Тогда верно:
3cos3(x+T)+2cos4(x+T)=3cos3x+2cos4x=3cos3(x-T)+2cos4(x-T).
Это соотношение должно выполняться при всех значениях переменной х, в частности и при х=0:
3cos 3T+2cos 4T=5 или 3cos 3T=5-2cos 4T.
Так как левая часть уравнения не превосходит трех, а правая – не
меньше трех, то уравнение равносильно следующей системе:
n = 3k
cos 3T = 1
T = 2πn / 3

, откуда 
, или m = 4k .

cos 4T = 1
T = πm / 2
T = 2πk

Этим показано, что если Т – период функции, то Т=2πk. Так как
верно y(x+2π)=3cos 3(x+2π)+2cos 4(x+2π)=3cos 3x+2cos 4x=y(x), то
наименьшее положительное число равно 2π.
Задачи для самостоятельного решения
1. Периодическая функция y=f(x) определена для всех действительных чисел. Ее период равен 4 и f(1)=3. Найдите значение выражения 7f(-3)+f(5).
Ответ: 24.
2. Периодическая функция y=f(x) определена для всех действительных чисел. Ее период равен 3 и f(0)=4. Найдите значение выражения 2f(3)-f(-3).
Ответ: 4.
3. Периодическая функция y=f(x) определена для всех действительных чисел. Ее период равен 5 и f(4)=-2. Найдите значение выражеОтвет: 0
ния (f(9)-f(-6))9.
4. Функция y=f(x) определена на всей числовой прямой и является
нечетной периодической функцией с периодом, равным 8 . На от220
резке [0;4] функция y=f(x) задана равенством f(x)=x2-4x. Определите количество нулей функции y=f(x) на отрезке [-2;5]. Ответ: 2
5.Функция y=f(x) определена на всей числовой прямой, является
нечетной периодической функцией с периодом, равным 4. На отрезке [-2;0] функция y=f(x) задана равенством f(x)=-x2-2x. Определите количество нулей функции y=f(x) на отрезке [-5;3]. Ответ: 4.
6. Функция y=f(x) определена на всей числовой прямой и является
четной периодической функцией с периодом, равным 4 . На отрезке
[0;2] функция y=f(x) задана равенством f(x)=2x2-4x+1. Сколько нулей имеет функция на отрезке [-3;3]?
Ответ: 6
7. Функция y=f(x) определена на всей числовой прямой и является
четной периодической функцией с периодом, равным 6 . На промежутке [-3;0] она задается формулой f(x)=x2+x+2. Найдите значение выражения f(10)-f(5)+f(-4).
Ответ: 6.
8. Найдите значение выражения f(1)+2f(-2)+4f(16), если известно,
что функция y=f(x) нечетная и периодическая с периодом, равным
10, а на отрезке [0;5] она определена формулой f(x)=10x-2x2.
Ответ: -48.
9. Функция y=f(x) определена на всей числовой прямой и является
периодической с периодом 7. На промежутке [-5;2) она задается
формулой f(x)=2-|x+1|. Найдите значение выражения 4f(17)-3f(-13).
Ответ: -4.
10. Функция y=f(x) определена на всей числовой прямой и является
периодической с периодом 6. На промежутке -2 ≤ x < 4 она задается
формулой f(x)=|x-2|-3. Найдите значение выражения 4f(11)-2f(-15).
Ответ: 4.
11. Функция y=f(x) определена на всей числовой прямой, является
четной и периодической с периодом 6. На отрезке [-3;0] она задана
равенством f(x)=x2-2x-2. Определите количество решений уравнения f(x)=1на отрезке [-7;5].
Ответ: 5.
12. Функция y=f(x) определена на всей числовой прямой, является
четной и периодической с периодом 8 . На отрезке [0;4] она задана
равенством f(x)=4x-x2. Определите количество решений уравнения
f(x)=1 на отрезке [-5;5].
Ответ: 5
13. Функция y=f(x) определена на всей числовой прямой и является периодической с периодом 6. При каждом x из промежутка (-2;4]
значение функции f(x) совпадает со значением функции g(x), опре221
3,
деленной кусочно: g ( x) = 
2< x≤4
2
 x − 1, − 2 < x ≤ 2
ражения f(6)+f(10)-2f(8).
. Найдите значение выОтвет: -4.
14. Функция у = f(x) определена на всей числовой прямой и является периодической с периодом 5. На рисунке 8 изображён график
этой функции при -3 ≤ x ≤ 2. Найдите значение выражения f(-10) –
f(-1)·f(8).
Ответ: 8.
Рис. 8
Рис. 9
Рис. 10
15. Функция у = f(x) определена на всей числовой оси и является
периодической с периодом 5. На рисунке 9 изображён график этой
функции при -3 ≤ x ≤ 2. Найдите значение выражения
.
Ответ: 0,5.
16. Функция у = f(x) определена на всей числовой оси и является
периодической с периодом 4. На рисунке 10 изображён график этой
функции при -2 ≤ x ≤ 2. Найдите значение выражения f(—7) + f(8)
— 3f(10).
Ответ: 12.
17. Функция у = f(x) определена на всей числовой оси и имеет период, равный 3, причём f(1)=2. График функции у = g(х)+5 совпадает с графиком f(x). Найдите значение выражения f(-5)+g(4).
Ответ: -1.
18. Периодическая функция у = f(x) определена для всех действительных чисел. Её период равен 5, а f(-1) = 1. Найдите f(—12), если
2f(3)-5f(9) = 9.
Ответ: 7
19. Функция f(x) периодическая с периодом, равным 2. На промежутке [0; 2) эта функция совпадает с функцией у = x2 - 2. Сколько
раз пересекаются графики функций у = f(x) и у = 1 на отрезке [1;7]?
Ответ: 3
20. Функция у = f(x) периодическая с периодом, равным 3. На промежутке (—1; 2] эта функция совпадает с функцией у = x2+2x.
222
Сколько раз пересекаются графики функций у = f(x) и у = 3 на отрезке [0; 11]?
Ответ: 4
21. Периодическая функция у = f(x) определена для всех действительных чисел. Её период равен 3. На отрезке [1; 7] у уравнения
f(x) = 0 ровно 3 корня. Найдите их произведение.
Ответ: 28
22. Функция f(x) является периодической с периодом 5. Определите, чему равен основной период функции f(x) + sin πx.
Ответ: 10
23. Найдите
Ответ: 12π
основной
период
функции
.
§ 6. Монотонность функции
Функция y=f(x) называется возрастающей на интервале (a;b),
если для любых x1 и x2 из этого интервала таких, что x1<x2, справедливо f(x1)<f(x2). Например, функции y=ax, y=logax при a>1,
y=arctg x, y=arcsin x, y = n x (n∈N) возрастают на всей своей области определения.
Рис. 11. График возрастающей функции
Функция y = f(x) называется убывающей на интервале (a;b), если для любых x1 и x2 из этого интервала таких, что x1<x2, справедливо f(x1)>f(x2). Например, функции y=ax, y=logax при 0<a<1,
y=arcctg x, y=arccos x убывают на всей своей области определения.
Рис. 12. График убывающей функции
223
Убывающие и возрастающие функции вместе образуют класс
монотонных функций. Монотонные функции обладают рядом специальных свойств.
1) функция f(х), монотонная на отрезке [а,b], ограничена на
этом отрезке;
2) сумма возрастающих (убывающих) функций является возрастающей (убывающей) функцией;
3) если функция f возрастает (убывает) и n – нечетное число, то
n
f также возрастает (убывает);
4) если f'(x)>0 для всех x∈(a,b), то функция y=f(x) является возрастающей на интервале (a,b);
5) если f'(x)<0 для всех x∈(a,b), то функция y=f(x) является
убывающей на интервале (a,b);
6) если f(x) – непрерывная и монотонная функция на множестве
Х, то уравнение f(x)=C, где С – данная константа, может иметь на Х
не более одного решения;
7) если на области определения уравнения f(x)=g(x) функция
f(x) возрастает, а функция g(x) убывает, то уравнение не может
иметь более одного решения.
Пример 1. Определим промежутки монотонности функции
5
y=x +2x4+x3+2.
Функция определена на всей числовой прямой. Найдем ее
производную: y’=5x4+8x3+3x2. y’=0 при x2(5x2+8x+3)=0, то есть
при х={0; -1; -0,6}. Определив знаки производной, получим, что
при при х∈[-1; -0,6] функция убывает, а при х∈(-∞; -1] ∪]-0,6; +∞)
– возрастает.
Пример 2. Решим неравенство 5x+2x>7.
Каждая из функций y=5x, y=2x непрерывна и возрастает на всей числовой прямой. Значит, какой же является и функция y=5x+2x . Легко видеть, что при х=0 функция y=5x+2x принимает значение 7. в
силу непрерывности и монотонности этой функции при х>0 имеем
5x+2x>7, при x<0 – 5x+2x<7. Следовательно, решения данного неравенства являются все x∈(-∞;0).
Задания для самостоятельного решения
1. Среди функций
укажите:
а) возрастающие; б) убывающие.
224
2. Какая из данных функций убывает на всей своей области определения:
а)
б)
в)
г)
;
е)
ж)
з)
д)
3.Укажите функцию, которая возрастает на всей своей области определения:
а)
б)
в)
г)
4. Укажите функцию, убывающую на промежутке (0; ):
б)
в)
г)
а)
5.Укажите график функции, возрастающей на отрезке [−3; 2].
y
y
1)
2)
1
0
3)
1
1
x
0
y
1
x
y
4)
1
1
1
1
0
0
x
x
6. Функция у = f(x) задана на отрезке [а; b]. На рисунке 13 изображён график её производной у = f'(x). Исследуйте на монотонность функцию у = f(x). В ответе укажите количество промежутков, на которых функция убывает.
Ответ: 3
Рис. 13
Рис. 14
225
7. Функция у = f(x) определена на промежутке (-5; 3). График её
производной изображён на рисунке 14. Укажите количество промежутков возрастания функции у = f(x).
Ответ: 3
Рис. 15
Рис. 16
8. Функция у = f(x) определена на отрезке [-5; 5], на рисунке 15
изображён график её производной. Определите количество промежутков возрастания функции у = f(x).
Ответ: 2
9. Функция у = f(x) определена на отрезке [-5; 5], на рисунке 16
изображён график её производной. Определите количество промежутков убывания функции у = f(x).
Ответ: 1
10. Решите уравнение:
а) x2x=8
Ответ:2
б) log2x=3-x
Ответ: 2
Ответ: -1
-x
в) 3 =x+4
Ответ: 2
г) 12x+5x=13x
Ответ: 1
д) 3x+4x=7x
Ответ: 3
е) log1/3 x=x-4
Ответ: 1
ж) 5 30 x + 2 = 3 − x
Ответ: 2
з) 4 − x = x + 14
4
226
§ 7. Точки экстремума. Наибольшее и наименьшее
значения функции
Точка xmax называется точкой (локального) максимума функции
y=f(x), если существует такой интервал (a,b), содержащий точку
хmax, что при всех x∈(a,b), x≠ xmax выполнено условие f ( x) < f ( xmax )
Рис. 17 Точка максимума
Точка xmin называется точкой (локального) минимума функции
y=f(x), если существует такой интервал (a,b), содержащий точку
хmin, что при всех x∈(a,b), x≠ xmin выполнено условие f(xmin)<f(x).
Рис. 18 Точка минимума
Точки, в которых функция достигает максимума и минимума,
называются точками экстремума, а значения функции в этих точках – экстремумами функции.
Критическими точками функции y=f(x) называются такие
точки x=x0, в которых f’(x0)=0 либо f’(x0) не существует, причем
сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Для любой дифференцируемой на интервале (a,b) функции
f(x) справедливы следующие утверждения:
1) если в точке x0 производная функции f(x) меняет знак с «+» на «», то х0 является точкой максимума функции f(x);
2) если в точке x0 производная функции f(x) меняет знак с «-» на
«+», то х0 является точкой минимума функции f(x).
Алгоритм исследования функции y=f(x) на экстремум
1. Найти область определения функции f(x).
2. Найти производную f '(x).
227
3. Определить критические точки, для этого:
а) найти корни уравнения f '(x)=0;
б) найти все значения x, при которых производная f '(x) не существует.
4. Координатную прямую разбить найденными точками на промежутки, в каждом из которых определить знак производной.
5. По приведенным выше утверждениям определить характер экстремума.
Значение функции f(x) в точке x0 называется наибольшим (наименьшим) значением этой функции на множестве А, если для любого
x∈A выполняется неравенство f(x0)≥f(x) (f(x0)≤f(x)).
Справедлива следующая теорема:
Дифференцируемая на (a,b) и непрерывная на [a,b] функция f(x)
достигает своих наибольшего и наименьшего значения на отрезке
[a,b] либо на концах отрезка, либо в одной из своих критических
точек, принадлежащих интервалу (a,b).
Пример 1.
Точка минимума там, где значение производной равно нулю и
при переходе через эту точку производная меняет знак с минуса на
плюс. Абсцисса такой точки равна 2.
Пример 2.
228
Задания для самостоятельного решения
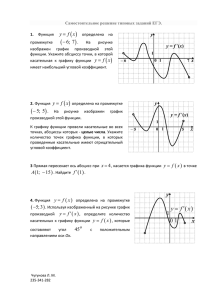
у
1. Функция y = f ( x) определена на
промежутке (– 3; 7). На рисунке 19
изображен график ее производной.
Найдите точку x0, в которой функция
y=f(x) принимает наибольшее значение.
Ответ: 1
у = f ′(x)
1
–3
1
0
7
х
Рис. 19
2. Функция у = f(x) задана на отрезке [a; b]. На рисунке 20 изображён график её производной у = f'(x). Исследуйте на экстремумы
функцию у = f(x). В ответе укажите количество точек максимума.
Ответ: 2
Рис. 20
Рис. 21
3. Функция у = f(x) определена на промежутке (а; b). На рисунке 21
изображён график её производной. Укажите число точек минимума
функции у = f(x) — Зх на промежутке (а; b).
Ответ: 3
229
4. Функция у = f(x) определена на промежутке (-6; 5). На рисунке
22 изображён график её производной. Укажите число точек минимума функции у = f(x) на промежутке (-6; 5).
Ответ: 2
5. Функция у = f(x) определена на промежутке (а; b). На рисунке 23
изображён график её производной. Укажите число точек минимума
функции у = f(x) на промежутке (а; b).
Ответ: 4
Рис. 22
Рис. 23
6. Функция у = f(x) определена на промежутке (а; b). На рисунке 24
изображён график её производной. Укажите число точек минимума
функции у = f(x).
Ответ: 5
Рис. 24
Рис. 25
7. Функция у = f(x) определена на промежутке [-5; 5]. На рисунке
25 изображён график её производной. Укажите точку, в которой
функция у = f(x) принимает наименьшее значение.
Ответ: 5
8. Функция у = f(x) определена на промежутке (-3; 4). На рисунке
26 изображён график её производной. Найдите абсциссу точки, в
которой функция f(x) принимает наибольшее значение. Ответ: -1
Рис. 26
Рис. 27
330
Рис. 28
9. Функция у = f(x) определена на промежутке (-4; 4). На рисунке
27 изображён график её производной. Найдите абсциссу точки, в
которой функция f(x) принимает наименьшее значение. Ответ: 2
10. Функция у = f(х) определена на промежутке (—5; 7). На рисунке
28 изображён график её производной. Найдите точку x0, в которой
функция у = f(x) принимает наименьшее значение на отрезке [-4;6].
Ответ: 4
11. Найдите наибольшее значение функции у = log2x + Iog2(4 - х) на
промежутке (0; 4).
Ответ: 2
12. Найдите сумму наибольшего и наименьшего значений функции
на отрезке [-1; 1].
Ответ: 15
13. Найдите сумму наибольшего и наименьшего значений функции
на отрезке [0,5; 1,5].
Ответ: 4
14. Найдите сумму наименьшего и наибольшего значений функции
на отрезке [0; 1].
Ответ: 9
15. Найдите разность между наибольшим и наименьшим значениями функции f(x)=log33(x3+3x2-9x+6) на отрезке [0; 3].
Ответ: 1
Ответ: 4
16. Найдите точку максимума функции
17. Найдите точку максимума функции
Ответ: -2
Ответ: -3
18. Найдите точку минимума функции
19. Найдите точку минимума функции
Ответ: 3,5
20. При каком значении функция
имеет минимум в точке
?
Ответ:3
21. Найдите количество целых чисел, принадлежащее множеству
значений функции
Ответ: 9
22. Функция у = f(x) задана на промежутке [–6; 4] (см. рисунок 29).
Укажите промежуток, которому принадлежат все точки экстремума.
y
1) [– 6; 0]
y=f(x
2) [0; 4]
3) [– 2; 3]
4
x
–
0
4) [– 3; 1]
Рис. 29
331
2
3
23. Найдите наибольшее значение функции y = 2,7 ⋅ e 3 x − x − 4 на
отрезке [1;3 ] .
Ответ: 2,7
24. Найдите наименьшее число, принадлежащее множеству значена отрезке [30˚;60˚].
Ответ: 1/2
ний функции
25. Найдите наименьшее целое число, принадлежащее множеству
значений функции
Ответ: 6
26. Найдите наименьшее целое значение функции
Ответ: 2
27. Найдите наименьшее значение функции
Ответ: -3
28. Найдите наименьшее значение функции
Ответ: -2
29. Найдите наибольшее значение функции
Ответ: 2
на
30. Найдите наибольшее значение функции
промежутке [5;7].
Ответ: -4
31. Найдите разность между наибольшим и наименьшим значениями функции
на отрезке [-2;3]
Ответ: 255,5
32. Найдите разность между наибольшим и наименьшим значениями функции
Ответ: 13
на отрезке
332
Приложение 1. Производные
Таблица производных основных элементарных функций
(С)’=0
(xn)’=nxn-1
(sin x)’=cos x
(cos x)’=-sin x
(tg x)’=1/cos2x
(ctg x)’=-1/sin2x
(ex)’=ex
(ax)’=ax ln a
(ln x)’=1/x
(logax)’=1/(x ln a)
Правила дифференцирования функций
(cu)’=cu’
(u±v)’=u’±v’
(uv)’=u’v+uv’
′
 u  u ' v − uv'
  =
v2
v
y=f(g(x)) y’=f’u(u) g’x(x), где u=g(x)
333
Приложение 2. Графики элементарных функций
334