Графики Прямая и обратная пропорциональность.

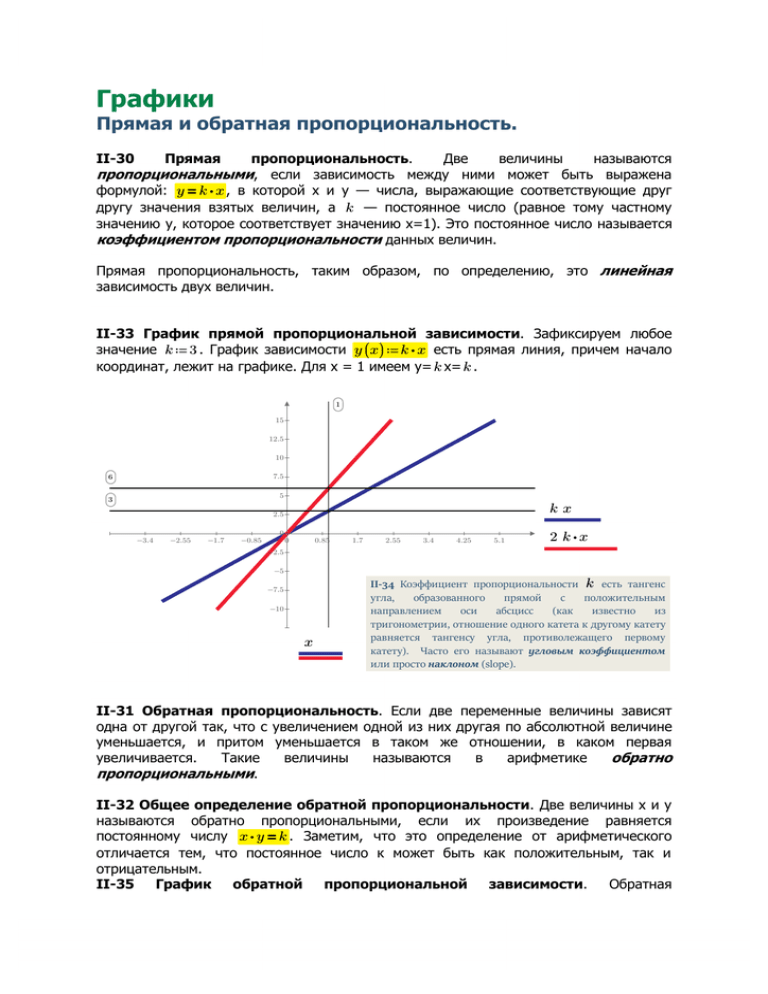
Графики
Прямая и обратная пропорциональность.
II-30
Прямая
пропорциональность.
Две
величины
называются
пропорциональными, если зависимость между ними может быть выражена
формулой: y ＝ k ⋅ x , в которой х и у — числа, выражающие соответствующие друг
другу значения взятых величин, а k — постоянное число (равное тому частному
значению у, которое соответствует значению х=1). Это постоянное число называется
коэффициентом пропорциональности данных величин.
Прямая пропорциональность, таким образом, по определению, это линейная
зависимость двух величин.
II-33 График прямой пропорциональной зависимости. Зафиксируем любое
значение k ≔ 3 . График зависимости y ((x)) ≔ k ⋅ x есть прямая линия, причем начало
координат, лежит на графике. Для х = 1 имеем у= k х= k .
1
15
12.5
10
7.5
6
5
3
kx
2.5
-3.4
-2.55
-1.7
-0.85
0
0
0.85
1.7
2.55
3.4
4.25
5.1
2 k⋅x
-2.5
-5
-7.5
-10
x
II-34 Коэффициент пропорциональности k есть тангенс
угла,
образованного
прямой
с
положительным
направлением
оси
абсцисс
(как
известно
из
тригонометрии, отношение одного катета к другому катету
равняется тангенсу угла, противолежащего первому
катету). Часто его называют угловым коэффициентом
или просто наклоном (slope).
II-31 Обратная пропорциональность. Если две переменные величины зависят
одна от другой так, что с увеличением одной из них другая по абсолютной величине
уменьшается, и притом уменьшается в таком же отношении, в каком первая
увеличивается.
Такие
величины
называются
в
арифметике
обратно
пропорциональными.
II-32 Общее определение обратной пропорциональности. Две величины х и у
называются обратно пропорциональными, если их произведение равняется
постоянному числу x ⋅ y ＝ k . Заметим, что это определение от арифметического
отличается тем, что постоянное число к может быть как положительным, так и
отрицательным.
II-35
График
обратной
пропорциональной
зависимости.
Обратная
5
График
обратной
пропорциональной
зависимости
Обратная
k
пропорциональность выражается формулой x ⋅ y ＝ k или y ((x)) ≔ ―в которой х и у —
x
числа, выражающие соответствующие друг другу значения взятых величин, а k —
постоянное
число
(называемое
коэффициентом
обратной
пропорциональности).
k
Построим график зависимости y ((x)) ≔ ―. Для х=1 имеем у= k .
x
−1
1
15
12.5
10
7.5
6
k
―
x
5
3
2.5
−3
-3.4
-2.55
-1.7
-0.85
0
0
0.85
1.7
2.55
3.4
4.25
5.1
-2.5
−6
2k
――
x
-5
-7.5
При неограниченном увеличении абсциссы х, ордината
кривой всё уменьшается, приближаясь к нулю, так что
кривая, по мере её продолжения направо, всё ближе и ближе
подходит к оси х­ов, но никогда её достигнуть не может:
-10
x
дробь
k
―никогда не может сделаться равной нулю.
x
k=3
b≔5
II-37 График двучлена первой степени y ((x)) ≔ k ⋅ x + b есть прямая линия,
параллельная прямой, изображающей прямую пропорциональность у = kх, и
отсекающая от оси у-ов отрезок равный b. Для х = 0 имеем у= k х= b .
15
12.5
10
7.5
5
5
kx
2.5
-3.4
-2.55
-1.7
-0.85
0
0
0.85
-2.5
-5
-7.5
-10
x
1.7
2.55
3.4
4.25
5.1
k⋅x+b