Непрерывные случайные величины: распределение и плотность
реклама

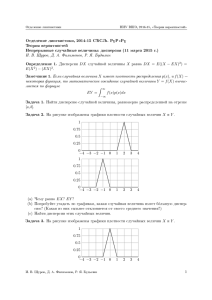
Отделение лингвистики НИУ ВШЭ, 2014-15, «Теория вероятностей» Отделение лингвистики, 2014-15 СЋСЉ. РүР«Рұ Теория вероятностей Непрерывные случайные величины: распределение и плотность (27 ноября 2013) И. В. Щуров, Д. А. Филимонов, Р. Я. Будылин Задача 1. Случайное число 𝑋 выбирается из отрезка [2, 5] таким образом, что вероятность её попадания на любой промежуток (лежащий в этом отрезке целиком) пропорциональная длине промежутка, то есть случайная величина распределена равномерно (a) Найти i) функцию распределения; ii) плотность случайной величины на отрезке [2, 5]. 𝑋. (b) Построить графики этих функций. (c) Найти вероятность события, состоящего в том, что 𝑋 попала в отрезок [2,5; 4]. Как бы вы стали искать это число, если бы знали только i) функцию распределения; б) функцию плотности. Задача 2. Найти функцию распределения и плотности для случайной величины, равномерно распределенной на отрезке [𝑎, 𝑏]. Задача 3. Рассмотрим график функции распределения случайной величины 𝑋 . 1 0.75 0.5 0.25 0 −4 −3 −2 −1 0 1 2 3 4 (a) Какие значения может принимать случайная величина? (b) Какова вероятность того, что (c) Какова вероятность того, что 𝑋 < 0? 𝑋 < 1? 𝑋 > 2? 𝑋 ∈ [0, 2]? 𝑋 ∈ [0, 1]? 𝑋 ∈ [0, 1/2]? 𝑋 ∈ [1, 3]? 𝑋 ∈ [1, 2]? 𝑋 ∈ [1, 3/2]? (d) Найти функцию плотности. Построить её график. Задача 4. Рассмотрим график плотности случайной величины 𝑋 . 0.75 0.5 0.25 0 −4 −3 −2 −1 0 1 2 3 4 1. Какие значения может принимать случайная величина? 2. Какова вероятность того, что 3. Какова вероятность того, что 𝑋 < 0? 𝑋 < 1? 𝑋 > 2? 𝑋 ∈ [0, 2]? 𝑋 ∈ [0, 1]? 𝑋 ∈ [0, 1/2]? 𝑋 ∈ [1, 3]? 𝑋 ∈ [1, 2]? 𝑋 ∈ [1, 3/2]? 4. Найти функцию распределения. Построить её график. И. В. Щуров, Д. А. Филимонов, Р. Я. Будылин 1