Определенный интеграл Римана. Определение, обобщенная

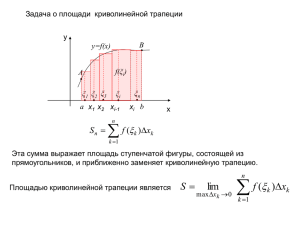
4
Определенный интеграл Римана. Определение, обобщенная теорема о среднем значении, интеграл с переменным верхним пределом, формула замены переменной, интегрирование по частям, некоторые неравенства.
4.1
Определение интеграла
Пусть функция f задана на [a, b]. Разобьем этот отрезок на части точками
xk : a = x0 < x1 < . . . < xn = b. Положим
∆xk = xk+1 − xk ; λ = max ∆xk .
k=0,n−1
Возьмем в каждом из отрезков [xk , xk+1 ] по точке γk и составим сумму
σ=
n−1
X
f (γk )(xk+1 − xk )
k=0
Говорят, что сумма σ при λ → 0 имеет (конечный) предел J, если для
любого ε > 0 существует δ > 0 такое, что неравенство λ < δ влечет неравенство |σ − J| < ε (при любом выборе точек xk и γk ).
Записывают это так:
J = lim σ .
λ→0
Определение 1. Конечный limλ→0 σ называется определенным интеграRb
лом функции f (в смысле Римана) на отрезке [a, b] и обозначается a f (x)dx.
В случае существования такого предела функция называется интегрируемой (по Риману) на отрезке .
4.2
Обобщенная теорема о среднем значении
Теорема 1. Пусть
1. f и g интегрируемы на [a, b],
2. m 6 f (x) 6 M для всех x ∈ [a, b],
3. функция g на [a, b] не меняет знака (g(x) 6 0 или g(x) > 0 для любого
x ∈ [a, b]).
Тогда существует γ ∈ [m, M ] такое, что
Z
b
Z
f (x)g(x)dx = γ
a
g(x)dx
a
1
b
(1)
При доказательстве теоремы 1 будут использоваться следующие свойства интеграла:
1. Если f и g интегрируемы на [a, b], то функция f g тоже интегрируема;
2. Если f интегрируема на [a, b], k ∈ R, то
b
Z
b
Z
f (x)dx ;
k f (x)dx = k
a
a
3. Если f и g интегрируемы на [a, b] и f (x) 6 g(x) при x ∈ [a, b], то
b
Z
b
Z
f (x)dx 6
a
g(x)dx ;
a
4. Если f интегрируема на [a, b] и неотрицательна, то
Rb
a
f (x)dx > 0.
Доказательство. Пусть сначала g(x) > 0. Тогда имеем
m g(x) 6 f (x)g(x) 6 M g(x)
при x ∈ [a, b]. На основании свойств 2 и 3 получаем
Z
m
b
Z
g(x)dx 6
a
b
Z
f (x)g(x)dx 6 M
a
b
g(x)dx
(2)
a
Rb
В силу свойства 4 имеем a g(x)dx > 0. Если он равен нулю, то из нераRb
венств (2) следует, что и a f (x)g(x)dx = 0, и утверждение теоремы очевидно. Если этот интеграл больше нуля, то, разделив на него обе части
неравенства (2) и полагая
Rb
γ=
a
f (x)g(x)dx
,
Rb
g(x)dx
a
придем к требуемому соотношению (1). От предположения g(x) > 0 легко перейти к предположению g(x) 6 0, так как изменение знака g(x) не
нарушит равенства.
Следствие 1. Если в условиях теоремы 1 функция f непрерывна, то формула (1) может быть записана в виде
Z
b
Z
f (x)g(x)dx = f (C)
a
b
g(x)dx ,
(3)
a
где C - некоторая точка отрезка [a, b].
Доказательство. Если считать, что m и M наименьшее и наибольшее значение f на [a, b], то по теореме Больцано-Коши о промежуточном значении
f (C) = γ в некоторой точке C ∈ [a, b]
2
Замечание 1 Теорема 1 и следствие 1 часто используются, когда g(x) ≡ 1
на [a, b]
В этом смысле теорема 1 называется теоремой о среднем значении для
определенного интеграла.
4.3
Определенный интеграл с переменным верхним пределом
Пусть f интегрируема на [a, b]. Тогда она интегрируемаRна любом отрезке
x
[a, x], где a 6 x 6 b, т.е. для любого x ∈ [a, b] существует a f (t)dt. Рассмотрим функцию
Z x
f (t)dt .
(4)
F (x) =
a
Эта функция, определенная на [a, b] называется интегралом с переменным верхним пределом.
Теорема 2. (непрерывность интеграла по верхнему пределу)
Если f интегрируема на [a, b], то функция F (x) непрерывна на этом
отрезке.
Доказательство. Пусть x ∈ [a, b], x + ∆x ∈ [a, b]. Тогда из (4) следует
Z
F (x+∆x) =
x+∆x
Z
f (t)dt =
a
x
Z
x+∆x
f (t)dt+
a
Z
x+∆x
f (t)dt = F (x)+
x
f (t)dt
x
Поэтому
Z
x+∆x
∆F (x) = F (x + ∆x) − F (x) =
f (t)dt
(5)
x
Так как функция f интегрируема на [a, b], то она ограничена на нем,
т.е. существует число M > 0 такое, что |f (x)| 6 M для любого x ∈ [a, b].
Учитывая этот факт имеем
Z
Z
x+∆x
x+∆x
|∆F (x)| = f (t)dt 6 |f (t)|dt 6 M |∆x| .
x
x
Следовательно, lim∆x→0 ∆F (x) = 0 для любого x ∈ [a, b], а это и означает
непрерывность F (x) в каждой точке x ∈ [a, b].
Теорема 3. (теорема Барроу)
Если f интегрируема
на [a, b] и непрерывна в точке x0 ∈ [a, b], то функRx
ция F (x) = a f (t)dt дифференцируема в точке x0 и F 0 (x0 ) = f (x0 ).
3
Доказательство. Покажем что
∆F (x0 )
= f (x0 ) ,
∆x→0
∆x
lim
где
∆F (x) = F (x0 + ∆x) − F (x0 ) , x0 + ∆x ∈ [a, b] .
Так как
1
∆x
Z
x0 +∆x
dx = 1, то f (x0 ) =
x0
1
∆x
Z
x0 +∆x
f (x0 )dx .
x0
Имеем
Z
Z x0 +∆x
x0 +∆x
∆F (x0 )
1
1
=
6
−
f
(x
)
(f
(t)
−
f
(x
))dt
|f
(t)
−
f
(x
)|dt
0 0
0
∆x
∆x x0
|∆x| x0
Пусть задано ε > 0. В силу непрерывности функции f в точке x0 существует δ = δ(ε) > 0 такое, что если |x−x0 | < δ, x ∈ [a, b], то |f (x)−f (x0 )| < ε.
Пусть |∆x| < δ, тогда |f (t) − f (x0 )| < ε для всех t, принадлежащих промежутку с концами x0 , x0 + ∆x и, следовательно, имеем
Z
x0 +∆x ∆F (x0 )
ε
dt = ε .
∆x − f (x0 ) < |∆x| x0
Это и означает, что
lim
∆x→0
∆F (x0 )
= f (x0 ) .
∆x
В случае, когда x0 совпадает с одним из концов отрезка [a, b] под F 0 (x)
следует понимать соответствующую одностороннюю производную F .
Следствие 2. Непрерывная на отрезке [a, b] функция имеет первообразную.
Доказательство. Из непрерывности f на [a, b] следует, что f интегрируема на [a, b] и согласно теореме
R x Барроу ее первообразной на [a, b] является,
например, функция F (x) = a f (t)dt.
4
4.4
Формула Ньютона-Лейбница
Теорема 4. (Формула Ньютона-Лейбница)
Пусть f непрерывна на [a, b]. Если функция Φ является ее первообразной на [a, b], то
b
Z
f (t)dt = Φ(b) − Φ(a) .
(6)
a
Доказательство. Положим
Z
x
f (t)dt .
F (x) =
a
Функция F является первообразной для f на [a, b]. Так как F и Φ две
первообразные одной и той же функции f на [a, b], то F (x) = Φ(x) + C при
a 6 x 6 b, где C - постоянная и, следовательно,
Z x
f (t)dt = Φ(x) + C .
a
Отсюда при x = a получаем C = −Φ(a). Следовательно,
Z x
f (t)dt = Φ(x) − Φ(a) .
a
Полагая здесь x = b, получаем (6).
Для краткости записи часто употребляют следующее обозначение
b
Φ(x)|a := Φ(b) − Φ(a) .
4.5
Формула замены переменной и интегрирование по
частям
Теорема 5. (формула замены переменной)
Пусть f непрерывна на отрезке X с концами a и b; функция ϕ имеет
непрерывную производную на отрезке Y с концами α и β, причем ϕ(Y ) ⊂
X, ϕ(α) = a, ϕ(β) = b. Тогда
Z
b
Z
β
f (ϕ(t))ϕ0 (t)dt .
f (x)dx =
a
(7)
α
Доказательство. Пусть Φ - первообразная f на X. Тогда при t ∈ Y имеет смысл сложная функция Φ(ϕ(t)), которая является первообразной для
функции f (ϕ(t))ϕ0 (t). По формуле Ньютона-Лейбница
Z
b
f (x)dx = Φ(b) − Φ(a) ,
a
5
β
Z
f (ϕ(t))ϕ0 (t)dt = Φ(ϕ(β)) − Φ(ϕ(α)) = Φ(b) − Φ(a)
α
Отсюда и следует формула (7).
Теорема 6. (интегрирование по частям)
Если функции u = u(x) и v = v(x) имеют непрерывные производные на
[a, b], то
Z
a
b
b
u(x)v 0 (x)dx = u(x)v(x)|a −
b
Z
v(x)u0 (x)dx
(8)
a
или коротко
Z
b
b
uv|a
udv =
a
Z
b
−
vdu .
a
Доказательство. Имеем
Z
b
(uv)0 dx =
b
Z
Z
udv +
a
b
vdu .
a
a
Все эти интегралы существуют, ибо подинтегральные функции непрерывны. По формуле Ньютона-Лейбница
b
Z
b
(uv) dx = uv .
0
a
a
Следовательно,
4.6
b
Z
b
uv|a =
Z
udv +
b
vdu .
a
a
Некоторые неравенства для интегралов
Теорема 7. (неравенство Гёльдера)
Пусть p, q ∈ (1, ∞), p1 + 1q = 1, функции f и g интегрируемы на [a, b],
тогда
Z
b
Z
|f (x)g(x)|dx 6
a
! p1
b
|f (x)|p dx
Z
a
a
6
b
! q1
|g(x)|q dx
.
Теорема 8. (неравенство Милковского)
Пусть f и g интегрируемы на [a, b], p > 1. Тогда
Z
! p1
b
p
|f (x) + g(x)| dx
Z
! p1
b
p
|f (x)| dx
6
Z
p
|g(x)| dx
+
a
a
! p1
b
.
a
Теорема 9. (неравенство Чебышёва)
Пусть f и g заданы на [a, b], причем f возрастает, а g убывает на [a, b].
Тогда
Z
b
f (x)g(x)dx 6
a
1
b−a
7
Z
b
Z
a
b
g(x)dx .
f (x)dx
a