и аберрации широкого сагиттального пучка лучей полностью

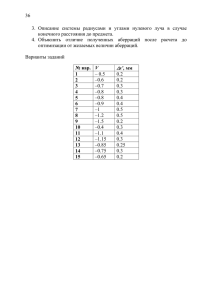
8
и аберрации широкого сагиттального пучка лучей полностью устранены.
Объектив построен с использованием метода М.М. Русинова.
Объектив модифицирован путем смещения плоскостей предмета и
изображения относительно первой и последней поверхностей объектива
соответственно (рис. 1.1.1б), благодаря чему возникает сферическая
аберрация третьего порядка.
Порядок выполнения работы:
1. Ввести в компьютер начальные данные в соответствии с
индивидуальным заданием (см. таблицу). Рассчитать ход лучей по
требованию 1 САРО, определить параксиальные характеристики.
Убедиться, что линейное увеличение системы V = –1, а входной и
выходной зрачки практически находятся на бесконечности. Это
свидетельствует о правильности ввода начальных данных. Вывести
вид пятен рассеяния по требованию 28. Убедиться, что пятно
рассеяния по всему полю одинаково, что свидетельствует об
отсутствии других аберраций, кроме сферической аберрации.
2. Вновь рассчитать ход лучей по требованию 1 и изучить столбцы,
содержащие продольную сферическую аберрацию ДS’(0),
поперечную сферическую аберрацию Y’(0) и волновую сферическую
аберрацию W(0). Принимая во внимание, что входные апертуры sin σ
для первого и третьего лучей соотносятся как 1: 0.5 , найти
показатели степени x, y, z, а также коэффициенты a, b и с в
выражениях:
ДS’(0) = a(sin σ)x,
(1.1.1)
y
Д’Y(0)=b(sin σ) ,
(1.1.2)
W(0)= c(sin σ)z.
(1.1.3)
Округлить показатели степени до целых значений и убедиться, что
сферическая аберрация третьего порядка в продольном выражении
имеет второй порядок, поперечная – третий, а волновая – четвертый.
Третий луч в общепринятой терминологии называется зоной зрачка.
3. Изучить влияние смещения плоскости установки ДS’Y на
поперечную сферическую аберрацию. Путем подбора найти
положение плоскости установки, при котором Y’(0)1 = –Y’(0)4, где
индексы обозначают номера лучей. Нетрудно убедиться, например,
используя требование 28 САРО, что пятно рассеяния при этом имеет
9
минимальный диаметр. Сравнить диаметр пятна рассеяния в
плоскости наилучшей установки и в плоскости Гаусса, используя
численные значения из таблицы. Сравнить смещение плоскости
наилучшей установки со значениями продольной сферической
аберрации относительно плоскости Гаусса. Убедиться, что
DS’Y=ДS’(0)2.
4. Ознакомиться с графической формой выдачи сферической
аберрации, для чего выполнить требование 5. График,
расположенный в левом верхнем углу экрана представляет
зависимость поперечной сферической аберрации (отложена по оси
OX) от тангенса апертурного угла в пространстве изображений tgσ’.
На экране представлен также масштаб графика: цена одного деления
шкалы в мм. По оси абсцисс штрихами отмечены значения tgσ’,
соответствующие первому, второму, третьему и четвертому лучам.
Нетрудно видеть, что и для внеосевых точек поля (второй и третий
графики), кривые линии идентичны таковым для осевой точки, что
свидетельствует об отсутствии внеосевых аберраций и постоянстве
сферической аберрации по полю изображения.
5. Для получения графиков волновой аберрации необходимо
выполнить требование 51. Волновая аберрация в длинах волн
представлена по оси ординат.
Варианты заданий:
Начальные данные для расчета хода лучей:
Положение предмета s1= –10 (A0=1; HA= –10);
положение
входного
зрачка
определяется
положением
апертурной
диафрагмы на третьей поверхности: ND=3, DD=0. Так как изображение
апертурной диафрагмы окажется близким к бесконечности, то для второго
параксиального луча можно задать sp=1000 (B0=1; HB=1000);
Размер предмета Y MAX = –8 мм;
Размер зрачка задается синусом апертурного угла в пространстве
предметов MU MAX= – 0.1;