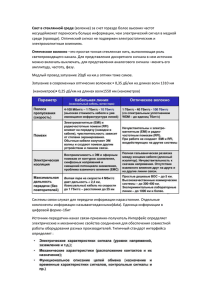
Обратим внимание на знак величины Z`m. Если конфокальная
реклама

Обратим внимание на знак величины Z'm. Если конфокальная поверхность разделяет воздух и стекло, а r > 0, то Z'm > 0. Поскольку у тонкого компонента с положительной оптической силой в соответствии с формулой (2.6) Z'm < 0, то добавление к нему конфокальной поверхности, расположенной на некотором расстоянии, позволяет добиться необходимой коррекции астигматизма. Линейное увеличение конфокальной поверхности, поскольку α = α', составляет: V = n / n' (4.18) 4.3. Близфокальная поверхность Если плоскость предмета проходит через вершину поверхности 0 (рис. 4.3), то такую поверхность М.М. Русинов называет близфокальной. Осевая точка предмета А совпадает с вершиной поверхности. Её изображение, очевидно, находится там же. Следовательно, плоскость Гаусса совпадает с плоскостью предмета. Гомоцентричность осевого пучка лучей не нарушается, поэтому сферическая аберрация отсутствует. Угол падения осевого луча на поверхность совпадает с углом этого луча с осью. Соответственно такое же совпадение существует между углом преломления и углом преломленного луча с осью в пространстве изображений. Из этого следует, что для близфокальной поверхности соблюдается закон синусов. В сочетании с устранением сферической аберрации этим гарантируется исправление комы в области близкой к оптической оси. Таким образом, близфокальная поверхность является одной из разновидностей апланатических поверхностей. ds B1 B r C O 4.3.Близфокальная поверхность Внеосевая точка плоского предмета В не лежит на близфокальной поверхности. Поэтому очевидно для этой точки кома и астигматизм будут иметь значения, отличные от нуля. Используя приём, который был использован при рассмотрении комы и астигматизма апланатической поверхности (формулы (4.13), (4.14) и соответствующий текст) можно показать, что эти аберрации будут иметь порядок выше третьего. Таким образом, доказывается, что кома и астигматизм третьего порядка у близфокальной поверхности отсутствуют. 60 Линейное увеличение V близфокальной поверхности равно единице, поскольку α n = α' n', а V = α n / α' n' = 1. (4.19) Близфокальную поверхность не рекомендуется задавать через углы первого параксиального луча с осью α, т. к. при высоте падения параксиального луча на поверхность h = 0 возникает неопределённость при вычислении радиуса поверхности по формуле: r = h (∆ n )/(∆ α n), (4.20) где в соответствии с формулой (4.18) ∆ α n = 0. На практике близфокальная поверхность, как правило, располагается в близи плоскости изображения, что оправдывает её название. При смещениях от плоскости изображения на величину существенно меньшую радиуса кривизны поверхности появляются аберрации третьего порядка: незначительная сферическая аберрация и несколько большие кома и астигматизм. Кривизна изображения близфокальной поверхности с высокой степенью точности может быть оценена по формуле (1.15). Близфокальные поверхности находят применение в коллективах телескопических систем, а также в компенсаторах кривизны изображения в объективах, где допускается малое расстояние изображения от последней поверхности. 4.4. Поверхность, концентричная зрачку Если центр поверхности совпадает с центром зрачка, то главные лучи, выходящие из центра зрачка, совпадают с нормалями к поверхности. Каждый главный луч может быть принят за вспомогательную оптическую ось, являющуюся осью симметрии внеосевого пучка как меридиональных, так и сагиттальных лучей. После преломления симметрия пучков относительно главного луча сохраняется. Благодаря этому отсутствуют кома и астигматизм. Положение предмета при этом роли не играет. В общем случае сферическая аберрация такой поверхности не устранена. Однако, поместив плоскость предмета на расстояние s в соответствии с формулой (4.5), можно устранить и сферичес-кую аберрацию. При этом условии поверхность окажется строго апланатичной и анастигматичной. Линейное увеличение поверхности, концентричной зрачку, не определено. Поэтому задать такую поверхность углами первого параксиального луча с осью невозможно. Добавление такой поверхности к сформированной части системы осуществляется на основе данных, полученных в результате расчёта хода лучей, а именно, положения выходного зрачка. Поверхность, концентричная зрачку, находит самостоятельное практическое применение в виде сферического зеркала в широкоугольных коллиматорах. Единственная аберрация такого зеркала – сферическая аберрация зеркала определяется формулой по формуле (2.26). 61