НИС 3-ий курс Домашнее задание 1 Исследование точности и

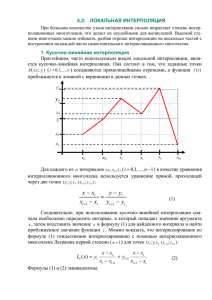
НИС 3-ий курс
Домашнее задание 1
Исследование точности и эффективности интерполяционных методов на примере
построения топографических карт активности головного мозга
В этом задании вам предстоит сравнить несколько методов интерполяции, реализованных в функции
griddata среды Matlab, с целью выбрать наиболее подходящую как с точки зрения точности, так и с
точки зрения вычислительных затрат.
Вы научитесь
1. Вычислять радиальную компоненту магнитного поля, регистрируемую магнетометром за
пределами сферического проводника.
2. Использовать функцию griddata для интерполяции значения градиента магнитного поля
3. Вычислять критерии качества работы алгоритма (невязка, временные затраты)
4. Наглядно представлять результат исследования в случае малого числа факторов
В вашем распоряжении имеются следующие две функции в среде Matlab
function [B] = B_Sphere_Magnetometer(Q,r0,r,or)
% Computes the projection of magnetic field vector B at a set of %locations r
outside the single layered spherical conductor
onto coil %orientation vectors
or. The magnetic field is assumed to be due to a %dipole Q located at r0 inside
the spherical conductor.
% r should be a 3xN matrix of locations where the field is to be computed
% Q is a 3x1 vector defining the 3 orthogonal dipole
% components oriented along x,y and z axis
% Note: argument vectors should be column vectors
function DisplayTopography(v,position)
% The function displays the topography vector(v) on a hemisphere. Sensor
locations(position) are also displayed.
% v – vector of N values
% position – Nx3 matrix of sensor positions, each row is sensor coordinate
Последняя функция использует интерполяцию для вычисления значения поля на регулярной сетке
точек на поверхности полусферы. Существует множество методов интерполяции, которые можно
использовать в данном контексте (метод ближайших соседей, метод линейной интерполяции, метод
кубических сплайнов, метод на основе функции Грина, метод и использованием сферических
гармоник и т. д.). Идеальный метод интерполяции на основе вектора измерений поля в небольшом
наборе точек должен максимально точно восстанавливать значения поля во всех точках регулярной
сетки и тратить на это минимум вычислительной мощности. В этой работе вы выясните, какой из
методов интерполяции реализованных в функции griddata является наиболее подходящим. В
частности, вы сравните следующие методы
'linear'
- Triangle-based linear interpolation (default)
'cubic'
- Triangle-based cubic interpolation
'nearest' - Nearest neighbor interpolation
'v4'
- MATLAB 4 griddata method, uses Green's function
Для оценки точности интерполяции мы воспользуемся следующим подходом. Мы сначала
смоделируем вектор измерений радиальной компоненты магнитного поля сенсорами магнитного поля
(магнетометрами). Эта операция осуществляется в строчке 58 скрипта
CompareInterpolationMethodsOneDipole.m, а координаты r0 и ориентация Q диполя задаются в строке
56. Далее, для отображения топографии нам необходимо осуществить интерполяцию этих значений
на точки регулярной сетки на полусфере и отобразить их. Эта процедура выполняется в строке 61
внутри функции DisplayTopography. Возникает вопрос: насколько точна та картина, которую мы
видим? На сколько интерполированные значения поля достоверно отражают действительные
значения поля?
В нашем распоряжении есть функция B_Sphere_Magnetometer(Q,r0,CoilPos,CoilOr), которая
позволяет вычислять значение проекции вектора поля, порожденного диполем с ориентацией Q,
находящегося в точке r0, в точках с координатами CoilPos на вектора ориентации(ортогональные
плоскости катушек) CoilOr.
Таким образом, все, что нам надо сделать это сравнить значения поля, Gtrue, вычисленные при
помощи B_Sphere_Magnetometer в точках регулярной сетки и интерполированные значения, Ginterp,
и сделать это для разных методов интерполяции, реализованных внутри функции griddata. Эти шаги
реализованы в строчках 68-83 скрипта.
При сравнении методов нас интересуют
1. Относительная квадратичная ошибка интерполяции E (строка 81)
2. Время вычисления интерполированных значений Т (строка 75)
Кроме того, некоторые интерполяционные методы для определенного подмножества точек не могут
решить задачу интерполяции и возвращают NAN . Процент таких точек (1-Goodpc) также может быть
использован как один из показателей качества работы алгоритма интерполяции.
Таким образом, все наши три критерия для хорошего метод интерполяции имеют маленькие значения,
а для плохого метода — большие. Удобно в данном случае воспользоваться следующим методом
отображения результатов. Для каждого метода мы имеем тройку чисел (E,T,1-Goodpc). Отобразим
каждый метод в виде точки в трехмерном пространстве с координатами (E,T,1-Goodpc), как это
сделано на рисунке ниже (строки 86-92 скрипта).
Анализируя результат, мы можем сказать, что с точки зрения точности и вычислительных затрат
наиболее предпочтительным является метод, использующий кубическую интерполяцию. Однако,
недостатком является относительно большое число точек, в которых интерполяция не была
выполнена (из-за сингулярности сплайн матрицы). Если время не является ограничительным
критерием, то метод, использующий функцию Грина (v4) позволяет обеспечить высокую точность
P erc e nta g e o f N A N s , pe rc en t
30
20
c u b ic
lin e a r
10
v4
0
5
10
0 .2
15
0 .1 5
20
I n te r p o la t io n e r r o r , p e rc e n t
интерполяции во всех точках.
n ea re st
25
0
0 .1
0 .0 5
C o m p u t a t io n t im e , s e c o n d s
Что надо сделать вам
В приведенном скрипте мы использовали лишь одну координату и ориентацию диполя. Вам
предстоит вычислить характеристики работы методов интерполяции средние для всех диполей
(одиночных), из объёма со следующими координатами [-0.1 : 0.1, -0.1 : 0.1, 0.0:0.15] м и оценить
разброс этих характеристик.
1. Создайте сетку позиций диполей, шаг можно взять равный 0.01 м, а ориентацию (Q)
выбирайте параллельную плоскости X-Y и ортогональную радиус вектору точки-координаты
диполя (r0)
2. Для каждого интерполяционного метода рассчитайте характеристики (E,T,1-Goodpc) для
каждого из диполей в указанном объеме.
3. Вычислите среднее (по всем диполям) значение ошибки, времени и процента NaN, а также
стандартное отклонение этих характеристик.
4. Отобразите результаты аналогично приведенному примеру, но для отображения дисперсии
замените точки на сферы с центром в точке, соответствующей среднему значению (E,T,1Goodpc) и радиусом пропорциональным стандартному отклонению каждого из параметров
(нарисовать 3 отдельных диаграммы)
5. Сравните с результатами, полученными по одному диполю и сделайте выводы.