3. Теория приближения функций
Реклама

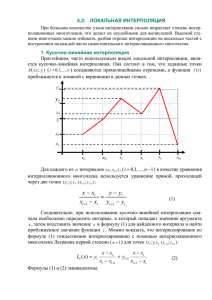
www.uchites.ru 3. Теория приближения функций 3.1. Постановка задач приближения функций В теории приближений изучаются методы приближения функций более простыми, хорошо изученными функциями, методы численного дифференцирования и численного интегрирования. При этом исследуемая приближаемая функция может быть задана как в аналитическом, так и дискретном виде (в виде экспериментальной таблицы). Пусть дана некоторая функция f ( x ) на отрезке x ∈ [a, b], которая является довольно сложной для исследования. Требуется заменить эту функцию некоторой простой, но хорошо исследуемой функцией (например, многочленом). Для этого с помощью f (x ) xi x0 x1 ... xn yi y0 y1 ... yn (3.1) строят таблицу (ее называют сеточной функцией), которую можно заменить (сгладить) простой функцией с контролируемой погрешностью. Рассмотрим два подхода к такой замене: 1. Пусть приближенная функция является многочленом n -й степени, f ( x ) = a 0 + a1 x + ... + a n x n , (3.2) где n + 1 - число узлов в таблице (3.1), с неизвестными параметрами ai , i = 0, n , так приближает сеточную функцию f ( x ) , что y i = f ( xi ), i = 0, n . В этом случае говорят, что функция (3.3) f (x ) интерполирует сеточную функцию (3.1), а сама задача приближения называется задачей интерполяции. Точки xi , i = 0, n называют узлами интерполяции, а условие (3.3) – условием интерполяции. Появляется возможность вычислить значения f (x ) не только в узлах интерполяции, но и между ними в точках ξ ∈ ( xi −1 , xi ), i = 1, n , причем f (ξ ) ≈ f (ξ ) . 2. При большом количестве точек xi , i = 0, n интерполяция требует большой 1 www.uchites.ru гладкости (по n-й производной), что практически выполнить невозможно. Поэтому сглаживание сеточной функции (3.1) осуществляют путем минимизации некоторого функционала, построенного с помощью (3.1) и многочлена (3.2) степени m , например, квадратичного функционала: S (a 0 , a1 ,..., a m ) = ∑ [y i − f ( xi )] , n 2 m << n . (3.4) i =0 Процедуру сглаживания в этом случае называют аппроксимацией заданной функции функцией (3.2), в частности, аппроксимацию с использованием функционала (3.4) называют аппроксимацией с помощью точечного метода наименьших квадратов. Если коэффициенты сглаживающей функции (3.2) определяются путем минимизации функционала b [ ] S (a 0 , a1 ,..., a m ) = ∫ f ( x ) − f ( x ) dx , 2 (3.5) a сглаживание называют интегральным методом наименьших квадратов. Если в качестве сглаживаемой функции задана экспериментальная таблица (3.1), то в методах сглаживания практически ничего не изменяется. Изменяются методы оценки погрешности сглаживания. 2 www.uchites.ru 3.2. Задача интерполяции Пусть на отрезке x ∈[a , b] задана функция f ( x ) , с помощью которой построена сеточная функция (3.1) или задана экспериментальная таблица (3.1). При сглаживании функции (или экспериментальной таблицы) с помощью интерполяции в соответствии с условием интерполяции (3.3) значение интерполирующей функции и значение заданной функции в узлах сетки должны быть одинаковыми, следовательно, погрешность интерполяции в узлах xi , i = 0, n равна нулю (рис. 3.1). y f(x) f(x) y0 x0 y1 x1 y2 ...................... yn x2 ....................... xn x Рис. 3.1. К задаче интерполяции Задача интерполяции имеет не единственное решение, но в случае, когда интерполирующей функцией является многочлен n-й степени (n+1 - число узлов интерполяции) вида (3.2) интерполяция имеет единственное решение, т.е. коэффициенты a 0 , Κ , a n определяются единственным образом. Действительно, используя таблицу (3.1), составим СЛАУ относительно неизвестных коэффициентов a 0 ,Κ , a n : n i = 0 ⎧a 0 + a1 x 0 + ... + a n x0 = y 0 ⎪ i = 1 ⎪a 0 + a1 x1 + ... + a n x1n = y1 ⎨ Λ ⎪Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ i = n ⎪⎩a 0 + a1 x n + ... + a n x nn = y n . (3.6) 3 www.uchites.ru Неоднородная СЛАУ (3.6) имеет единственное решение для коэффициентов a0 ,..., an , т.к. определитель матрицы этой СЛАУ не равен нулю: ⎛1 x 0 ⎜ ⎜1 x1 det⎜ ⎜. . ⎜1 x n ⎝ . x0n ⎞ ⎟ . x1n ⎟ ≠ 0, . . ⎟⎟ . x nn ⎟⎠ поскольку все значения узлов интерполяции различны между собой и ни одна из строк не является линейной комбинацией других строк. Таким образом, задача полиномиальной интерполяции имеет единственное решение, т.к. коэффициенты a0 ,..., an могут быть выбраны единственным образом. 3.2.1. Интерполяционный полином Лагранжа Для полиномиальной интерполяции можно не решать СЛАУ (3.6), а составить многочлен (3.2) следующим образом : запишем систему полиномов n-й степени l0 = ⎧1, x = x0 ( x − x1 )( x − x 2 )...( x − x n ) =⎨ ( x0 − x1 )( x0 − x 2 )...( x0 − x n ) ⎩0, x = xi , i = 1, n l1 = ⎧1, x = x1 ( x − x0 )( x − x 2 )...( x − x n ) =⎨ ( x1 − x0 )( x1 − x 2 )...( x1 − x n ) ⎩0, x = xi , i = 0, 2, n ………………………………………………………………… ln = ⎧1, x = x n ( x − x0 )( x − x1 )...( x − x n−1 ) =⎨ ( x n − x0 )( x n − x1 )...( x n − x n−1 ) ⎩0, x = xi , i = 0, n − 1. Составим линейную комбинацию этих полиномов (их количество равно n+1) с коэффициентами линейной комбинации, равными значениям yi сеточной функции (3.1), получим многочлен n -й степени: n Ln ( x ) = ∑ yi i =0 (x − x0 )(x − x1 )...(x − xi −1 )(x − xi+1 )...(x − xn ) . (xi − x0 )(xi − x1 )...(xi − xi−1 )(xi − xi +1 )...(xi − xn ) Полином (3.7) называют интерполяционным полиномом (3.7) Лагранжа n-й степени, т.к. он, во-первых, удовлетворяет условию интерполяции Ln ( xi ) = yi , i = 0, n , и, во-вторых, имеет n-ю степень. Интерполяционный многочлен Лагранжа обладает тем недостатком, что в 4 www.uchites.ru случае, когда добавляются новые узлы интерполяции в таблице (3.1), все слагаемые в (3.7) необходимо пересчитывать. Выпишем наиболее употребляемые полиномы L1 ( x) и L2 ( x) : 1) Для таблицы с двумя узлами интерполяции xi , xi +1 xi xi +1 yi yi +1 L1 ( x) = yi x − xi +1 x − xi + yi +1 ; xi − xi +1 xi +1 − xi 2) Для таблицы с тремя узлами интерполяции xi −1 , xi , xi +1 xi −1 xi xi +1 yi −1 yi yi +1 L2 ( x) = y i −1 ( x − xi )( x − xi +1 ) ( x − xi −1 )( x − xi +1 ) + yi + ( xi −1 − xi )( xi −1 − xi +1 ) ( xi − xi −1 )( xi − xi +1 ) + y i +1 ( x − xi −1 )( x − xi ) . ( xi +1 − xi −1 )( xi +1 − xi ) 3.2.2. Интерполяционный полином Ньютона При построении интерполяционного полинома в форме Ньютона используется понятие разделенной разности, представляющее собой аналог понятия производной применительно к сеточным функциям. Разделенной разностью сеточной функции (3.1) нулевого порядка в узлах xi , i = 0, n называются значения этой функции в этих узлах f ( xi ) = y i , i = 0, n. Определение 1. Разделенной разностью функции (3.1) первого порядка в узлах xi , i = 0, n − 1 называют отношение f ( xi , xi +1 ) = f ( xi +1 ) − f ( xi ) yi +1 − yi = , xi +1 − xi xi +1 − xi i = 0, n − 1 Определение 2. Разделенной разностью функции (3.1) второго порядка в узлах xi , i = 0, n − 2 называют отношение 5 www.uchites.ru f ( x i + 2 ) − f ( x i +1 ) f ( x i +1 ) − f ( x i ) − x i + 2 − x i +1 x i +1 − x i f ( x i +1 , x i + 2 ) − f ( x i , x i +1 ) = = f ( x i , x i +1 , x i + 2 ) = xi + 2 − xi xi + 2 − xi y i + 2 − y i +1 y i +1 − y i − x i + 2 − x i +1 x i +1 − x i , = xi + 2 − xi i = 0, n − 2. Определение 3. Разделенной разностью функции (3.1) n-го порядка в узле x 0 называют отношение f ( x0 , x1 ,..., x n ) = f ( x1 ,..., xn ) − f ( x0 ,..., xn−1 ) . x n − x0 С использованием разделенных разностей интерполяционный полином Ньютона записывается в форме: N n ( x) = f ( x0 ) + f ( x0 , x1 )( x − x0 ) + f ( x0 , x1 , x 2 )( x − x0 )( x − x1 ) + + ... + f ( x0 , x1 ,..., x n )( x − x0 )( x − x1 )...( x − x n −1 ). (3.8) Отметим, что при добавлении новых узлов первые члены многочлена Ньютона остаются неизменными. Если функция задана в точках x0 , x1 ,..., xn , то при построении интерполяционного многочлена Ньютона удобно пользоваться таблицей, называемой таблицей разделенных разностей, пример которой для n = 4 приведен в табл. 3.1. Таблица 3.1 x0 f (x0 ) x1 f (x1) f (x0 , x1 ) x2 x3 f (x2 ) f (x3 ) f (x1, x2 ) x4 f (x4 ) f (x2 , x3 ) f (x3 , x4 ) f (x0 , x1, x2 ) f (x1, x2 , x3 ) f (x2 , x3 , x4 ) f (x0, x1, x2, x3) f (x1, x2, x3, x4 ) f (x0, x1, x2, x3, x4) Для повышения точности интерполяции в сумму (3.8) могут быть добавлены новые члены, что требует подключения дополнительных интерполяционных узлов. При этом безразлично, в каком порядке подключаются новые узлы. Этим формула Ньютона выгодно отличается от формулы Лагранжа. 3.2.3. Погрешность полиномиальной интерполяции Ясно, что в узлах интерполяции погрешность интерполяционного полинома 6 www.uchites.ru Ln (x) или N n (x) равна нулю: ⎧ Ln ( xi ) − yi ⎫ ⎬=0, ⎨ ⎩ N n ( xi ) − y i ⎭ i = 0, n . Погрешность L n ( x) − f ( x) , представляющая собой разность между значением интерполяционного многочлена L n (x) и значением функции f ( x ) в точке x , не совпадающей с узлом интерполяции имеет вид: () () f x − Ln x = f (n +1) (ξ ) ( x − x0 )( x − x1 )...( x − x n ), ξ ∈ (a, b) . (n + 1)! (3.9) x - точка, в которой ищется погрешность (не совпадает с узлами интерполяции). Поскольку точка ξ ∈ ( a, b) неизвестна, то вместо погрешности (3.9) вводится верхняя оценка погрешности в виде f ( x ) − Ln ( x ) ≤ max f (n+1) ( x ) x∈[a ,b ] (n + 1)! ( x − x0 )( x − x1 )...( x − x n ) , (3.10) которая и используется на практике. Таким образом, погрешность интерполяции зависит как от величины соответствующей производной приближаемой функции, так и от расположения узлов. Минимизировать погрешность приближения достаточно гладкой функции на отрезке [a, b] полиномом степени n можно, расположив узлы интерполяции следующим образом: xi = a+b b−a + t i , i = 0, n , 2 2 где t i = cos 2i + 1 π n - корни полинома Чебышева H n ( x) = cos(n arccos x) (или в рекуррентном виде H 0 ( x) = 1, H 1 ( x) = x , H n ( x) = 2 xH n −1 ( x) − H n − 2 ( x) ). Отметим также, что такое расположение узлов интерполяции гарантирует сходимость интерполяционного полинома к приближаемой функции при повышении числа узла интерполяции (степени полинома), тогда как при равномерном распределении узлов в ряде случаев может наблюдаться расходимость (такая ситуация хорошо иллюстрируется известным примером 7 www.uchites.ru Рунге, в котором функция f ( x) = 1 1 + 25 x 2 приближается интерполяционным полиномом на отрезке [−1,1] ). Пример 3.1. Построить совпадающий с функцией интерполяционный f ( x ) = 3 x , x ∈ [− 1,1] в точках полином Лагранжа, x0 = −1, x1 = 0, x2 = 1. Вычислить значение сеточной функции и оценить погрешность интерполяции в точке x * = 0,5. Р е ш е н и е. Составим сеточную функцию и занесем ее в таблицу. Поскольку n = 2 , то необходимо построить интерполяционный полином L2 (x ) . xi x0 = −1 x1 = 0 x2 = 1 yi y0 = 1 3 y1 = 1 y2 = 3 L2 ( x ) = y 0 = (x − x0 )(x − x2 ) (x − x0 )(x − x1 ) (x − x1 )(x − x2 ) + y1 + y2 = (x1 − x0 )(x1 − x2 ) (x2 − x0 )(x2 − x1 ) (x0 − x1 )(x0 − x2 ) 2 2 4 x + x + 1. Проверим условия интерполяции L2 (− 1) = 1 3 ; L2 (0) = 1; L2 (1) = 3. 3 3 Значение сеточной функции в x * = 0,5 точке вычислим по интерполяционному многочлену y (0,5) ≈ L2 (0,5) = 1,8333 . Верхнюю оценку погрешности интерполяционного многочлена определим в соответствии с выражением (3.10) ( ) ( ) f x * − L2 x * ≤ max f ′′′( x ) x∈[−1, 1] 3! (x * )( )( − x0 x * − x1 x * − x 2 ) ; max f ′′′( x ) = max 3 x ⋅ ln 3 3 = 31 ⋅ ln 3 3 = 3,978 ; x∈[−1,1] x∈[−1,1] 4 ⎞ 3,978 ⎛2 (0,5 + 1)(0,5 − 0)(0,5 − 1) = 0,249. 30,5 − ⎜ ⋅ 0,25 + ⋅ 0,5 + 1⎟ ≤ 3 6 ⎠ ⎝3 8 www.uchites.ru Поскольку функция f ( x) = 3 x известна, то можно вычислить точное значение абсолютной погрешности в точке x * = 0,5 * 4 ⎞ ⎛2 3 x − L2 (x * ) = 30,5 − ⎜ ⋅ 0,25 + ⋅ 0,5 + 1⎟ = 0,1012, 5 ⎠ ⎝3 т.е. верхняя оценка погрешности примерно в 2,5 раза превышает абсолютную погрешность в точке x * = 0,5 . Пример 3.2. Для заданной таблицы xi x0 = −1 x1 = 0 x2 = 2 yi y0 = 1 3 y1 = 1 y2 = 9 составить интерполяционный полином Ньютона. Р е ш е н и е. Таблица задана с неравномерным шагом, поэтому для решения задачи воспользуемся многочленом Ньютона с разделенными разностями (формула (3.8)) N 2 ( x ) = f ( x0 ) + f ( x0 , x1 )(x − x0 ) + f (x0 , x1 , x 2 )( x − x0 )( x − x1 ) , где f ( x0 ) = y 0 = 1 3 ; f ( x0 , x1 ) = y1 − y 0 1 − 1 3 2 = = ; 0 +1 3 x1 − x0 y 2 − y1 y1 − y 0 9 −1 1−1 3 − − x 2 − x1 x1 − x0 10 f ( x0 , x1 , x 2 ) = = 2 − 0 0 +1 = . x 2 − x0 2 +1 9 Таким образом, N 2 ( x ) = 10 2 16 x + x + 1. 9 9 Условия интерполяции соблюдены: N 2 (− 1) = 1 3 ; N 2 (0) = 1; N 2 (2) = 9. 9 www.uchites.ru 10 www.uchites.ru 3.2.4. Сплайн-интерполяция Рассмотренная в предыдущих разделах интерполяция, когда интерполяционный полином строится сразу по всем узлам интерполяции называется глобальной интерполяцией. При этом увеличение числа узлов автоматически приводит к повышению степени полинома, и как следствие, к проявлению его колебательных свойств (рис. 3.2). Поэтому обычную полиномиальную интерполяцию осуществляют максимум по 3-4 узлам. Интерполяцию по нескольким узлам таблицы (3.1), называют локальной. y y Ln(x) Nn(x) L2(x) f(x) y0 y1 x0 y2 x1 x2 L2(x) yn ....................... xn x* x Рис. 3.2. Проявление колебательных Рис. 3.3. Локальная интерполяция по свойств глобального x каждым трем узлам интерполяционного полинома Однако, такая локальная интерполяция с помощью Ln или N n страдает тем недостатком, что интерполирующая функция в узлах стыковки полиномов имеет непрерывность только нулевого порядка, т.е. интерполирующая функция принадлежит классу функций C 0 (см. рис. 3.3 для L2 , N 2 в узле x * ). От этих недостатков свободна сплайн-интерполяция, которая требует непрерывности в узлах стыковки локальных многочленов по производным соответственно порядка один, два, и т.д. Определение. Сплайном - степени m дефекта r называется (m-r) раз непрерывно дифференцируемая функция, которая на каждом отрезке [ xi − xi −1 ], i = 1, n. представляет собой многочлен степени m. 11 www.uchites.ru Наиболее распространенными в науке и технике являются сплайны 3-й степени дефекта один, т.е. m = 3⎫ ⎬ ⇒ m − r = 3 − 1 = 2, r =1 ⎭ т.е. дважды непрерывно дифференцируемый многочлен 3-й степени на каждом отрезке [ xi , xi −1 ], i = 1, n. . Сплайны, удовлетворяющие условию интерполяции, называются интерполяционными. Основным достоинством интерполяционного кубического сплайна дефекта один является следующее: этот сплайн обладает минимумом интегральной кривизны на всем заданном отрезке [a , b] по сравнению с другими интерполяционными функциями f ( x ) , т.е. b b ∫ [S ′′( x)] dx ≤ ∫ [ f ′′( x)] dx 2 a 2 . a Геометрически это означает, что если тяжелую упругую нить повесить на ряд гвоздей, то она примет форму кубического сплайна дефекта 1, приведенную на рис. 3.4. Рис. 3.4. Тяжелая упругая нить, геометрически представляющая собой кубические сплайны дефекта один Рассмотрим алгоритм построения интерполяционного кубического сплайна S (x ) , i = 1, n дефекта один в соответствии с таблицей (3.1). Кубический полином S i (x) на отрезке x ∈ [xi −1 , xi ] имеет четыре неизвестных коэффициента. Количество отрезков [xi −1 , xi ] в соответствии с таблицей (3.1) равно n . Для определения 4 × n коэффициентов имеются следующие условия в узлах интерполяции: условие интерполяции непрерывность сплайна S ( xi ) = y i , i = 0, n ; S ( xi − 0) = S ( xi + 0) , непрерывность производных 1-го порядка i = 1, n − 1 ; S ′( xi − 0) = S ′( xi + 0) , i = 1, n − 1 ; 12 www.uchites.ru непрерывность производных 2-го порядка S ′′( xi − 0) = S ′′( xi + 0) , i = 1, n − 1 . Таким образом, всего имеется ( n + 1) + 3( n − 1) = 4n − 2 условий. В качестве двух недостающих условий задают значения производных 1-го или 2-го порядка в узлах x 0 и x n . Для вывода используем значения S ′′( x0 ) = S ′′( xn ) = 0 . В этом случае сплайн называется естественным. Пусть S ′′( x) = q ( x) . На отрезке [xi −1 , xi ] рассмотрим поведение функции q (x) (см. рис.3.5) . qi qi-1 xi-1 q(x)=L1(x) hi q(x)=L1(x) qi+1 hi+1 xi+1 xi Рис. 3.5. Поведение функций S ′′(x) на элементарных отрезках Поскольку сплайн является многочленом 3-й степени, то на каждом отрезке [ xi −1 , xi ] 2-я производная будет линейна. Найдем ее с помощью интерполяционного многочлена Лагранжа 1-й степени L1 ( x) : q( x) = qi −1 x − xi x − xi −1 + qi . xi −1 − xi xi − xi −1 (3.11) Выражение (3.11) уже удовлетворяет условиям непрерывности производных 2-го порядка. Действительно, подставим в (3.11) x = xi − 0 , получим q ( xi − 0) = qi . Затем, выписывая выражение (3.11) для отрезка x ∈[ xi , xi +1 ] q ( x) = qi x − xi xi +1 − x + qi +1 , hi +1 hi +1 x ∈ [xi , xi +1 ] , i = 1, n − 1 и подставляя в него xi + 0 вместо x , получим q ( xi + 0) = qi , что и требовалось показать. Для нахождения сплайна проинтегрируем дважды выражение (3.11), получим 13 www.uchites.ru S ( x ) = q i −1 ( xi − x ) 3 ( x − xi −1 ) 3 + qi + C1 x + C2 , 6hi 6hi (3.12) где C1 и C2 найдем из удовлетворения значений сплайна (3.12) в узлах xi −1 , xi условиям интерполяции ⎧ ( xi − xi −1 ) 3 ( xi −1 − xi −1 ) 3 + qi + C1 xi −1 + C 2 ⎪S ( xi −1 ) = y i −1 = qi −1 6hi 6hi ⎪ ⎨ 3 3 ⎪S ( x ) = y = q ( xi − xi ) + q ( xi − xi −1 ) + C x + C . i i −1 i 1 i 2 ⎪ i 6hi 6hi ⎩ Решая эту СЛАУ относительно C1 , C2 и подставляя их в (3.12), найдем следующее выражение для сплайна степени 3 дефекта 1: S ( x) = qi −1 (xi − x )3 6hi + qi ⎛y h ⎞ + ⎜⎜ i − qi i ⎟⎟( x − xi −1 ), 6⎠ ⎝ hi (x − xi −1 )3 6hi ⎛y h + ⎜⎜ i −1 − qi −1 i 6 ⎝ hi ⎞ ⎟⎟( xi − x ) + ⎠ (3.13) x ∈ [xi −1 , xi ]. В этом сплайне узловые значения для вторых производных qi пока неизвестны. Будем искать их из условий непрерывности первых производных в узлах xi . Для нахождения производной S ′( xi + 0) запишем (3.13) для отрезка [ xi , xi +1 ] ( xi +1 − x) 3 ( x − xi ) 3 ⎛ y i h ⎞ + qi +1 + ⎜⎜ − qi i +1 ⎟⎟( xi +1 − x) + 6hi +1 6hi +1 6 ⎠ ⎝ hi +1 ⎛ y i +1 h ⎞ ⎜⎜ − qi +1 i +1 ⎟⎟( x − xi ), x ∈ [xi , xi +1 ]. 6 ⎠ ⎝ hi +1 S ( x) = qi (3.14) Вычисляя от (3.13) и (3.14) производные первого порядка и подставляя в них значение x = xi , получим S ′( xi − 0) = qi −1 hi h y − yi −1 + qi i + i , 6 3 hi S ′( xi + 0) = −qi hi +1 h y − yi − qi +1 i +1 + i +1 . 3 6 hi +1 Приравняем эти выражения в соответствии с условиями непрерывности первых производных в узлах интерполяции xi , получим qi −1 hi h + hi +1 h y − yi yi − yi −1 + qi i + qi +1 i +1 = i +1 − , i = 1, n − 1 ; 6 3 6 hi +1 hi (3.15) 14 www.uchites.ru q 0 = q n = 0. (3.16) Система (3.15) с заданными краевыми условиями (3.16) – СЛАУ относительно qi = S ′′( xi ) , i = 1, n − 1 имеет трехдиагональную матрицу и, следовательно, ее можно решать методом прогонки. Подставляя найденные qi , i = 0, n в (3.13), получим кубические сплайны дефекта один на каждом отрезке x ∈ [xi −1 , xi ] , i = 1, n. Таким образом, определяющими выражениями для определения кубических сплайнов дефекта один являются выражения (3.13), (3.15), (3.16). Пример 3.3. Для заданной таблицы с h = xi − xi −1 = 1 = const построить интерполяционный кубический сплайн дефекта один, выписав соответствующие уравнения на каждом отрезке x ∈ [xi −1 , xi ] , i = 1, 4 . Проверить непрерывность сплайна и его производных до второго порядка включительно в узле x * = 2. i 0 1 2 3 4 xi x0 = 1 x1 = 2 x2 = 3 x3 = 4 x4 = 5 yi y0 = 1 y1 = 3 y2 = 6 y3 = 9 y 4 = 21 qi 0 18 7 − 30 7 102 7 0 Р е ш е н и е. Под заданной таблицей сформируем дополнительную строку для вторых производных S ′′( xi ) ≡ qi сплайнов, которая заполняется по мере их вычисления (сразу можно вписать в нее q 0 = q 4 = 0 ). Для узлов x1 = 2; x2 = 3; x3 = 4 с учетом q 0 = q 4 = 0 составляется СЛАУ (3.15) относительно неизвестных q1 , q 2 , q3 15 www.uchites.ru y − y1 y1 − y 0 1 ⎧2 − =1 q1 + q 2 = 2 ⎪ 6 1 1 i = 1: ⎪3 y 3 − y 2 y 2 − y1 2 1 ⎪1 − =0 ⎨ q1 + q 2 + q3 = i = 2 :⎪6 3 6 1 1 y − y3 y3 − y 2 ⎪1 2 q 2 + q3 = 4 − = 9. ⎪ i = 3 : ⎩6 3 1 1 Вычисляются прогоночные коэффициенты по формулам Ai = − ci d − ai Bi −1 ; Bi = i , i = 1,2,3 ; bi + ai Ai −1 bi + ai Ai −1 102 2 4 3 1 a1 = c3 = 0, A1 = − ; B1 = ; A2 = − ; B2 = − ; A3 = 0; B3 = 7 5 15 2 4 и значения qi = Ai qi +1 + Bi , i = 3,2,1 : q3 = A3 q 4 + B3 = B3 = 102 7 ; q 2 = A2 q3 + B2 = − 4 102 2 30 ⋅ − =− ; 15 7 5 7 1 ⎛ 30 ⎞ 3 18 q1 = A1q 2 + B1 = − ⋅ ⎜ − ⎟ + = . 4 ⎝ 7 ⎠ 2 7 Заносим эти значения в дополнительную строку таблицы и для каждого из четырех интервалов выписываем уравнения сплайна (3.13). (x1 − x )3 (x − x0 )3 1⎞ ⎛y + ⎜ 0 − q0 ⋅ ⎟( x1 − x ) + 6 ⋅1 6 ⋅1 6⎠ ⎝ 1 1⎞ 18 ⎛y (x − 1)3 + (2 − x ) + 108 (x − 1), x ∈ [1; 2]; + ⎜ 1 − q1 ⋅ ⎟( x − x0 ) = 6⎠ 42 42 ⎝ 1 i = 1 : S I (x ) = q0 + q1 (x − x ) i = 2 : S II ( x ) = q1 2 3 6 ⋅1 + q2 (x − x1 )3 6 ⋅1 1⎞ ⎛y + ⎜ 1 − q1 ⎟( x 2 − x ) + 6⎠ ⎝ 1 ⎛ 30 ⎞ 3 + ⎜ − ⎟( x − 2 ) + ⎝ 42 ⎠ 1⎞ 18 ⎛y (3 − x )3 + ⎜ 2 − q 2 ⎟( x − x1 ) = 6⎠ 42 ⎝ 1 108 (3 − x ) + 282 (x − 2), x ∈ [2; 3]; + 42 42 16 www.uchites.ru (x3 − x )3 (x − x2 )3 + ⎛ y 2 1⎞ ⎜ − q 2 ⎟( x 3 − x ) + 6 ⋅1 6 ⋅1 6⎠ ⎝ 1 1⎞ 30 102 ⎛y 3 (x − 3)3 + 282 (4 − x ) + + ⎜ 3 − q3 ⎟( x − x 2 ) = − (4 − x ) + 6⎠ 42 42 42 ⎝ 1 276 (x − 3), x ∈ [3; 4]; + 42 i = 3 : S III ( x ) = q 2 + q3 (x4 − x )3 + (x − x3 )3 1⎞ ⎛y + ⎜ 3 − q 3 ⎟( x 4 − x ) + 6 ⋅1 6 ⋅1 6⎠ ⎝ 1 1⎞ 102 ⎛y (5 − x )3 + 276 (5 − x ) + 21(x − 4), x ∈ [4, 5]. + ⎜ 4 − q 4 ⎟( x − x 3 ) = 6⎠ 42 42 ⎝ 1 i = 4 : S IV ( x ) = q3 q4 Проверим правильность построения сплайна для узла x * = 2. К данному узлу примыкают кривые S1 ( x ) и S 2 ( x ) . S1 (2 − 0) = 3; S II (2 + 0 ) = 3; 120 120 ; S II′ (2 + 0 ) = ; 42 42 108 108 ; S II′′ (2 + 0) = S1′′(2 − 0) = . 42 42 S1' (2 − 0) = 3.2.5. Тригонометрическая интерполяция Поскольку многие явления в природе имеют циклический характер, широкое практическое применение получила интерполяция дискретных периодических функций тригонометрическими полиномами вида: T ( x) = ∑ (a k cos(α k x) + bk sin(α k x) ) , k где α k = 2πk - частота k -ой гармоники, L - период, a k , bk - коэффициенты L разложения. Такой подход позволяет представить сложную циклическую структуру в виде суперпозиции простых периодических функций (элементарных гармоник). Рассмотрим таблично заданную на периоде L функцию y i ( xi ) с равномерным распределением узлов ( xi = x0 + ih , h = L / n , i = 0, n) . 17 www.uchites.ru xi x0 x1 ... xn yi y0 y1 ... yn Тогда, если n - четно ( n = 2m ), существует единственный интерполяционный тригонометрический полином Tm (x) степени m = n/2, удовлетворяющий условиям Tm ( xi ) = y i , i = 0, n : ⎛ 2πk ⎞ ⎛ 2πk ⎞ ( x − x0 ) ⎟ + bk sin ⎜ ( x − x0 ) ⎟ . Tm ( x) = a 0 + ∑ a k cos⎜ ⎝ L ⎠ ⎝ L ⎠ k =1 m Коэффициенты разложения определяются следующим образом: a0 = 1 n −1 ∑ yi , n i =0 ak = 2 n −1 2 n −1 i i , cos( 2 π ) = y k b y i sin( 2πk ) , k = 1, m − 1 , ∑ ∑ i k n n n i =0 n i =0 am = 1 n −1 ∑ yi cos(iπ ) . n i =0 Отметим, что периодичность исходной функции y i ( xi ) предполагает, что y 0 = y n . Если это условие не выполнено, то построенный тригонометрический полином будет удовлетворять условиям интерполяции во всех узлах, кроме последнего, т.е. Tm ( xi ) = y i , i = 0, n − 1 . В последнем узле будет выполняться условие периодичности Tm ( xn ) = Tm ( x0 ) . Найдите больше информации на сайте Учитесь.ру (www.uchites.ru)! 18