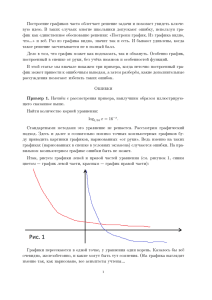
b g z b g z b g x b gc h− zb gc h F HGIKJ F F F HGIKJ ≥ F

ÇÀÄÀ×ÍÈÊ
M1731. Íàðèñîâàíî 60 çâåçäî÷åê, è äâîå ïîî÷åðåäíî
çàìåíÿþò ëþáóþ çâåçäî÷êó íà öèôðó. Äîêàæèòå, ÷òî
âòîðîé ìîæåò ñäåëàòü òàê, ÷òîáû ïîëó÷åííîå ÷èñëî
äåëèëîñü íà 13.
Ðàçîáüåì ïîëó÷åííîå ÷èñëî íà 10 øåñòåðîê öèôð. Âòîðîé
ìîæåò ëåãêî ñäåëàòü òàê, ÷òîáû â êàæäîé øåñòåðêå ïåðâûå
òðè öèôðû ñîâïàäàëè ñ ïîñëåäíèìè (abcabc). Ïîëó÷åííîå ÷èñëî áóäåò äåëèòüñÿ íà 1001 è, ñëåäîâàòåëüíî, íà 13.
Í.Âàñèëüåâ, Á.Ãèíçáóðã
M1732. à) Ìíîæåñòâà À è Â íà ïðÿìîé ñîäåðæàò ïî n
òî÷åê. Åñëè âñå òðîåòî÷èÿ èç ìíîæåñòâà À çàíóìåðîâàòü â êàêîì-ëèáî ïîðÿäêå, òî âñå òðîåòî÷èÿ èç ìíîæåñòâà  ìîæíî çàíóìåðîâàòü â òàêîì ïîðÿäêå, ÷òî
âñÿêèå äâà òðîåòî÷èÿ èç À è Â, èìåþùèå îäèíàêîâûå
íîìåðà, áóäóò ðàâíû (ïðè íàëîæåíèè ñîâïàäóò). Äîêàæèòå, ÷òî ìíîæåñòâà À è Â ðàâíû.
á*) Ñîõðàíèò ëè óòâåðæäåíèå ñèëó, åñëè â íåì «òðîåòî÷èÿ» çàìåíèòü íà «äâîåòî÷èÿ»?
à) Íóæíî äîêàçàòü, ÷òî ìíîæåñòâà À è Â ðàâíû èëè, êàê
åùå ãîâîðÿò, èçîìåòðè÷íû. Ñíà÷àëà îòìåòèì, ÷òî ñïèñîê
ðàññòîÿíèé ìåæäó âñåâîçìîæíûìè ïàðàìè òî÷åê èç ìíîn n +1
÷èñåë, ñîâïàäàåò ñ ïîäîáíûì
æåñòâà À, â êîòîðîì
2
ñïèñêîì äëÿ ìíîæåñòâà  – ýòî íåïîñðåäñòâåííî âûòåêàåò
èç óñëîâèÿ çàäà÷è. Îòñþäà ìîæíî çàêëþ÷èòü, ÷òî äèàìåòðû ìíîæåñòâ À è  ðàâíû. Ïîýòîìó ìíîæåñòâà À è Â
ìîæíî ðàçìåñòèòü íà îäíîì îòðåçêå I, êîíöû êîòîðîãî
ïðèíàäëåæàò êàê À, òàê è Â.
Òåïåðü íóæíî äîêàçàòü, ÷òî ìíîæåñòâà À è Â ëèáî
ñîâïàëè, ëèáî ñèììåòðè÷íû îòíîñèòåëüíî òî÷êè Q, êîòîðàÿ ÿâëÿåòñÿ ñåðåäèíîé îòðåçêà I.
Ðàññìîòðèì âîçìîæíîå âçàèìîðàñïîëîæåíèå òî÷åê ìíîæåñòâà À è ìíîæåñòâà  íà îòðåçêå I ñ êîíöàìè α è β .
Åñëè òî÷êà γ ∈ A , òî ëèáî γ ∈ B , ëèáî òî÷êà, ñèììåòðè÷íàÿ òî÷êå γ îòíîñèòåëüíî Q, ïðèíàäëåæèò Â, òàê êàê ïî
óñëîâèþ äëÿ òðîåòî÷èÿ ( α , β , γ ) èç ìíîæåñòâà À â
ìíîæåñòâå  èìååòñÿ ðàâíîå òðîåòî÷èå. Åñëè äâå òî÷êè γ
è δ , ñèììåòðè÷íûå îòíîñèòåëüíî Q, ïðèíàäëåæàò ìíîæåñòâó À, òî îáå îíè ïðèíàäëåæàò è ìíîæåñòâó Â.
Îáîçíà÷èì Ñ = A 7 B , â ìíîæåñòâå Ñ âûäåëèì ìàêñèìàëüíîå ïîäìíîæåñòâî C1 , ñèììåòðè÷íîå îòíîñèòåëüíî òî÷êè
Q. Òîãäà Ñ = C0 7 C1 . Çàìåòèì, ÷òî ìíîæåñòâî A1 = À –
– Ñ è B1 =  – Ñ íå ïåðåñåêàþòñÿ è ñèììåòðè÷íû
îòíîñèòåëüíî òî÷êè Q. Åñëè ìíîæåñòâî A1 (à çíà÷èò è B1 )
ïóñòîå, òî À ñîâïàäàåò ñ Â. Åñëè ìíîæåñòâî C0 ïóñòîå, òî
À ñèììåòðè÷íî  îòíîñèòåëüíî Q. Ââèäó ýòîãî äîñòàòî÷íî
óáåäèòüñÿ, ÷òî õîòÿ áû îäíî èç äâóõ ìíîæåñòâ C0 è A1
îáÿçàòåëüíî ÿâëÿåòñÿ ïóñòûì.
Äîïóñòèì ïðîòèâíîå: íè C0 , íè A1 ïóñòûìè íå ÿâëÿþòñÿ.
Èç îïðåäåëåíèé ýòèõ ìíîæåñòâ è ïðîâåäåííîãî àíàëèçà
ñëåäóåò, ÷òî ïîëíûé ñïèñîê (ñ ó÷åòîì êðàòíîñòåé) ðàññòîÿíèé ìåæäó ïàðàìè òî÷åê, îäíà èç êîòîðûõ ïðèíàäëåæèò
C0 , à äðóãàÿ A1 , ñîâïàäàåò ñ ïîëíûì ñïèñêîì ðàññòîÿíèé
ìåæäó ïàðàìè òî÷åê, îäíà èç êîòîðûõ ïðèíàäëåæèò C0 , à
äðóãàÿ B1 (îáäóìàéòå äåòàëüíî ýòî óìîçàêëþ÷åíèå!).
Íî ìàêñèìàëüíîå ðàññòîÿíèå ìåæäó òî÷êàìè ìíîæåñòâà
C0 è òî÷êàìè ìíîæåñòâà A1 íå ðàâíî ìàêñèìàëüíîìó
ðàññòîÿíèþ ìåæäó òî÷êàìè C0 è òî÷êàìè B1 ! ×òîáû â ýòîì
óäîñòîâåðèòüñÿ, êàæäîå èç íàçâàííûõ ìíîæåñòâ óäîáíî è
äîñòàòî÷íî ïðåäñòàâèòü äâóìÿ òî÷êàìè: êðàéíåé ëåâîé è
êðàéíåé ïðàâîé. Ïðè ýòîì íóæíî âñïîìíèòü, ÷òî A1 è B1
b
6*
g
!
«ÊÂÀÍÒÀ»
ñèììåòðè÷íû îòíîñèòåëüíî òî÷êè Q, à C0 – ñòðîãî àñèììåòðè÷íî îòíîñèòåëüíî Q.
Çíà÷èò, ïðîòèâîðå÷èå ïîëó÷åíî, è óòâåðæäåíèå äîêàçàíî.
á) Íå ñîõðàíèò. Ïðèâåäåì ïðèìåð äâóõ ìíîæåñòâ À è Â,
êàæäîå èç êîòîðûõ ñîñòîèò èç 9 òî÷åê. Ïðè ýòîì ïîëíûé
ñïèñîê ðàññòîÿíèé ìåæäó òî÷êàìè À (èç 36 ÷èñåë) ñîâïàäàåò ñ àíàëîãè÷íûì ñïèñêîì ìíîæåñòâà Â, íî ýòè ìíîæåñòâà íå ðàâíû (íå èçîìåòðè÷íû). Ìíîæåñòâî À çàäàåòñÿ
ñëîâîì abaabbab,
ìíîæåñòâî  – ñëîâîì abbabaab (áóê
âà â ñëîâå – ðàññòîÿíèå ìåæäó ñîñåäíèìè òî÷êàìè ìíîæåñòâà). Ïðè à = 1 è b = 2 ìíîæåñòâà
À è Â ïðåäñòàâëåíû íà ðèñóíêå.
Îñòàåòñÿ îòêðûòûì âîïðîñ: èçìåíèòñÿ ëè îòâåò ýòîãî
ïóíêòà, åñëè âñå ðàññòîÿíèÿ â ìíîæåñòâå À ñ÷èòàòü
ðàçëè÷íûìè?
Â.Ïðîèçâîëîâ
bg
M1733. Íåïðåðûâíàÿ ôóíêöèÿ f x òàêîâà, ÷òî f = f −1
bg
è f 0 = 1. Äîêàæèòå
ðàâåíñòâî
1
1
x − f x dx = .
2
z
bg
y
B
C
S
0
Ãðàôèê
ôóíêöèè
y = f x ñèììåòðè÷åí
îòíîñèòåëüíî áèññåêòðèñû ïåðâîãî êîîðäèíàòíîãî óãëà ó = õ
(ñì. ðèñóíîê). Çíà÷èò,
S1 = S4 , à S2 = S3 .
Ïîýòîìó ìîæíî çàïèñàòü
bg
z
1
0
bg
x − f x dx =
z
S
S!
S"
A
O
D
x
x
z
x0
c f b xg − xhdx + cx − f b xghdx =
0
x0
1
= S1 + S3 =
1
2
S ABCD =
1
2
.
Ê.Êàèáõàíîâ
F sin x IJ = cos x íà
M1734. Äîêàæèòå, ÷òî óðàâíåíèå G
H x K
FG 0; π IJ íå èìååò ðåøåíèé ïðè β ≤ 3 , íî èìååò åäèíñòâåíH 2K
β
íîå ðåøåíèå ïðè β > 3 .
Òàêèå çàäà÷è îáû÷íî ñâîäÿòñÿ ê èññëåäîâàíèþ ôóíêöèè
ñ ïîìîùüþ ïðîèçâîäíûõ. Òðóäíîñòü ñîñòîèò â òîì, ÷òîáû
ñóìåòü óäà÷íî âûáðàòü èññëåäóåìóþ ôóíêöèþ.
Èññëåäîâàíèå óðàâíåíèÿ çàäà÷è ìû íà÷íåì ñ î÷åâèäíîãî
çàìå÷àíèÿ: ïðè β ≤ 0 îíî ðåøåíèé íå èìååò.  ñàìîì äåëå,
ïîñêîëüêó sin x < x ïðè x > 0, òî ïðè β ≤ 0 íà âñåì
β
sin x
π
≥ 1.
âûïîëíåíî íåðàâåíñòâî
èíòåðâàëå 0;
x
2
FG IJ
H K
Ïóñòü β > 0 . Çàìåòèì, ÷òî ôóíêöèÿ
FG sin x IJ
H x K
FG
H
IJ
K
β
− cos x îáðà-
FG π IJ , ÷òî è
H 2K
ùàåòñÿ â íîëü â òåõ æå òî÷êàõ èíòåðâàëà 0;