Вопросы к вступительным испытаниям по Обществознанию 2009 г

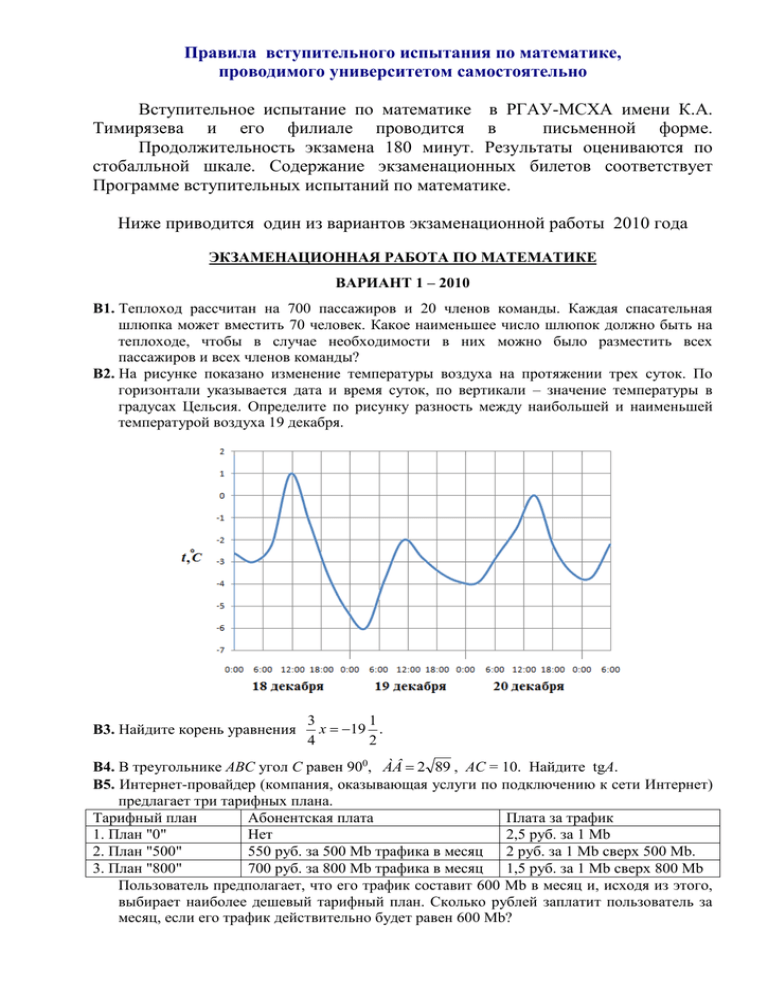
Правила вступительного испытания по математике,
проводимого университетом самостоятельно
Вступительное испытание по математике в РГАУ-МСХА имени К.А.
Тимирязева и его филиале проводится в
письменной форме.
Продолжительность экзамена 180 минут. Результаты оцениваются по
стобалльной шкале. Содержание экзаменационных билетов соответствует
Программе вступительных испытаний по математике.
Ниже приводится один из вариантов экзаменационной работы 2010 года
ЭКЗАМЕНАЦИОННАЯ РАБОТА ПО МАТЕМАТИКЕ
ВАРИАНТ 1 – 2010
В1. Теплоход рассчитан на 700 пассажиров и 20 членов команды. Каждая спасательная
шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на
теплоходе, чтобы в случае необходимости в них можно было разместить всех
пассажиров и всех членов команды?
B2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По
горизонтали указывается дата и время суток, по вертикали – значение температуры в
градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей
температурой воздуха 19 декабря.
В3. Найдите корень уравнения
3
1
x  19 .
4
2
В4. В треугольнике ABC угол C равен 900, ÀÂ  2 89 , АС = 10. Найдите tgA.
В5. Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет)
предлагает три тарифных плана.
Тарифный план
Абонентская плата
Плата за трафик
1. План "0"
Нет
2,5 руб. за 1 Mb
2. План "500"
550 руб. за 500 Мb трафика в месяц 2 руб. за 1 Mb сверх 500 Mb.
3. План "800"
700 руб. за 800 Mb трафика в месяц 1,5 руб. за 1 Mb сверх 800 Mb
Пользователь предполагает, что его трафик составит 600 Mb в месяц и, исходя из этого,
выбирает наиболее дешевый тарифный план. Сколько рублей заплатит пользователь за
месяц, если его трафик действительно будет равен 600 Mb?
В6. Найдите площадь треугольника, вершины которого имеют координаты (1;6), (10;6), (7;8).
В7. Найдите значение выражения 1217  58 : 6056 .
В8. На рисунке изображен график производной функции y = f(x), определенной на интервале
(–7; 14). Найдите количество точек максимума функции f(x) на отрезке [–6; 9].
B9. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота
которого равны 1. Найдите объем параллелепипеда.
В10. Для одного из предприятий-монополистов зависимость объёма спроса на продукцию q
(единиц в месяц) от её цены p (тыс. руб.) задаётся формулой: q = 210 – 15p. Определите
максимальный уровень цены p (в тыс. руб.), при котором значение выручки предприятия
за месяц r = qp составит не менее 360 тыс. руб.
B11. Найдите точку максимума функции y = (x + 9)e9 – x.
B12. Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления,
затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной
воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
sin y  5 sin x  2  0,
6 sin 2 x  5 sin x  cos 2 y  0.
С1. Решите систему уравнений 
С2. В кубе ABCDA1B1C1D1 точки E и F – середины ребер A1B1 и С1D1 соответственно.
Найдите косинус угла между прямыми AE и BF.
2
 x 8 
3 0.
2
 x  4x  3 
С3. Решите неравенство log 3 x  2 
С4. Дана трапеция ABCD с боковыми сторонами АВ = 36, CD = 34 и верхним основанием ВС
1
= 10. Известно, что cos ABC   . Найдите BD.
3
С5. Найдите все значения а, при каждом из которых функция f ( x)  x 2  x  a 2  5 x имеет
хотя бы одну точку максимума.
С6. Перед каждым из чисел 4. 5, …, 8 и 11, 12, …, 19 произвольным образом ставят знак
плюс или минус, после чего к каждому из образовавшихся чисел первого набора
прибавляют каждые из образовавшихся чисел второго набора, а затем все 45 полученных
результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму
можно получить в итоге?
3