Урок по тригонометрии No1

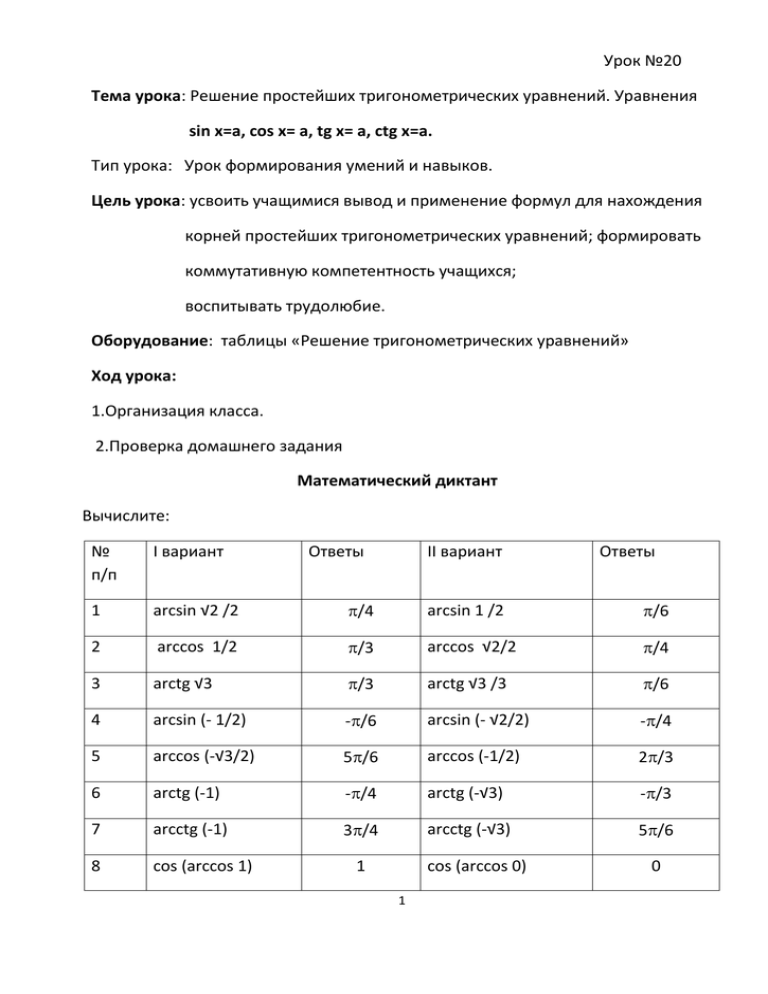
Урок №20
Тема урока: Решение простейших тригонометрических уравнений. Уравнения
sin x=a, cos x= a, tg x= a, ctg x=a.
Тип урока: Урок формирования умений и навыков.
Цель урока: усвоить учащимися вывод и применение формул для нахождения
корней простейших тригонометрических уравнений; формировать
коммутативную компетентность учащихся;
воспитывать трудолюбие.
Оборудование: таблицы «Решение тригонометрических уравнений»
Ход урока:
1.Организация класса.
2.Проверка домашнего задания
Математический диктант
Вычислите:
№
п/п
I вариант
1
arcsin √2 /2
/4
arcsin 1 /2
/6
2
arccos 1/2
/3
arccos √2/2
/4
3
arctg √3
/3
arctg √3 /3
/6
4
arcsin (- 1/2)
-/6
arcsin (- √2/2)
-/4
5
arccos (-√3/2)
5/6
arccos (-1/2)
2/3
6
arctg (-1)
-/4
arctg (-√3)
-/3
7
arcctg (-1)
3/4
arcctg (-√3)
5/6
8
cos (arсcos 1)
Ответы
II вариант
1
cos (arсcos 0)
1
Ответы
0
9
sin (arcsin √2 /2)
√2/2
sin (arcsin 1 /2)
1/2
10
arcsin (sin /4)
/4
arcsin (sin /3)
/3
11
arсcos (cos /6)
/6
arсcos (cos /4)
/4
12
arccos ( sin /6)
/3
arccos ( sin /3)
/6
А теперь обменяйтесь тетрадями и оцените результаты диктанта друг у
друга. За каждый верный ответ 1 балл.
3. Мотивация мыслительной деятельности учащихся. Сообщение темы и
задач урока.
Как известно из алгебры, квадратные уравнения решаются с помощью
формул их корней. Сегодня мы будем учиться решать тригонометрические
уравнения, которые содержат неизвестную величину, входящую по знак
тригонометрической функции. Причем сначала научимся решать простейшие
тригонометрические уравнения вида sin x=a, cos x= a, tg x= a, ctg x=a.
Поэтому наша задача вывести и запомнить основные формулы корней для
решения таких уравнений.
Результаты наших выводов мы поместим в таблицу.
Решение тригонометрических уравнений
Формулы корней
Примеры
sin x=a,
1)sin x= 3 – решений нет.
если |а|>1, то решений нет.
2) sin x= √3/2
|а|≤ 1
x= (-1)k arcsin √3/2+ k, kZ;
x= (-1)k arcsin a+ k, kZ.
x= (-1)k arcsin √3/2+ k, kZ;
Частные случаи:
Ответ: x= (-1)k arcsin √3/2+ k, kZ;
sin x = 0; x= k, kZ.
3) sin (x+ /6) = 1.
sin x = 1; x= /2+2k, kZ.
x+ /6= /2+2k, kZ;
sin x = -1; x= -/2+2k, kZ.
x= /2-/6+2k, kZ.
2
x= /3+2k, kZ.
Ответ: x= /3+2k, kZ.
Примеры
cos x= a,
1) сos x = - 25- решений нет.
если |а|>1, то решений нет.
2) сos x = √3/2,
|а|≤ 1
x= ± arcos √3/2+ 2n, nZ.
x= ± arcos a+ 2k, kZ.
x= ± /6+ 2n, nZ.
Частные случаи:
Ответ: x= ± /6+ 2n, nZ.
cos x = 0; x=/2+ k, kZ.
3) cos (x- /4) = 1;
cos x = 1; x= 2k, kZ.
x- /4= 2n, nZ.
cos x = -1; x= +2k, kZ.
x= /4+ 2n, nZ.
Ответ: x= /4+ 2n, nZ.
tg x= a, а- любое число
1) tg x = 5 ;
x= arctg a +k, kZ.
x= arctg 5 +n, nZ.
tg x = 0, x= k, kZ.
2) tg x/ 4 =1,
x/4= arctg 1 +n, nZ.
x/4= /4+n, nZ.
x= +4n, nZ.
Ответ: x= +n, nZ. (Вместо 4n, можно
указывать наименьший период n).
ctg x=a, а- любое число
1) 3 ctg 2x – 1= 0; ctg 2x = 1/3;
x= arcctg a +k, kZ.
2x = arcctg 1/3 +n, nZ;
ctg x = 0, x=/2+ k, kZ.
x= 1/2 arcctg 1/3 +(/2)n, nZ;
3
Ответ: x= 1/2 arcctg 1/3 +(/2)n, nZ;
2) сtg x/7 =0; x/7=/2+ n, nZ.
x= 7/2+ 7n, nZ.
Ответ: x= 7/2+ 7n, nZ.
Для того чтобы сэкономить время на уроке, предварительно, надо распечатать
и выдать каждому ученику таблицу решения тригонометрических уравнений.
IV. Осмысление изученного материала.
Выполнение упражнений стр. 117 № 57 (четные).
V. Подведение итогов урока.
VI. Домашнее задание.
Прочитать § 12, выучить формулы корней, пользуясь таблицей,
основные тригонометрические формулы, решить № 57 (нечетные).
4
повторить