Вариант 1 Часть 1 Ответом в заданиях первой части является

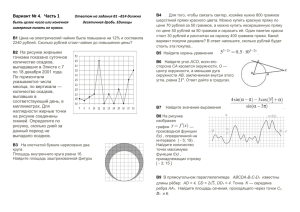
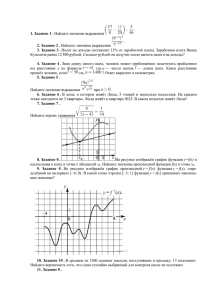
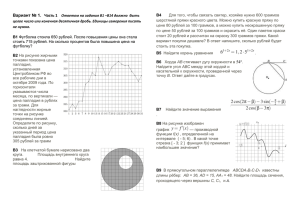
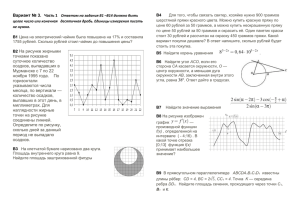
Вариант 1
Часть 1
Ответом в заданиях первой части является целое число или конечная десятичная дробь
В1. Держатели дисконтной карты книжного магазина получают при покупке скидку 3%. Книга
стоит 400 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
В2. На диаграмме показано распределение выплавки меди в 10 странах мира (в тысячах тонн) за
2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое
место — Казахстан. Какое место занимала Канада?
В3. Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1
см  1 см (см. рис.). В ответе запишите
S

.
В4. Для того, чтобы связать свитер, хозяйке нужно 400 граммов шерстяной пряжи синего цвета.
Можно купить синюю пряжу по цене 60 рублей за 50 граммов, а можно купить неокрашенную
пряжу по цене 50 рублей за 50 граммов и окрасить её. Один пакетик краски стоит 10 рублей и
рассчитан на окраску 200 граммов пряжи. Какой вариант покупки дешевле? В ответ напишите,
сколько рублей будет стоить эта покупка.
log  4 x  5 
 7.
В5. Решите уравнение 2 8
В6. Через концы A, B дуги окружности в 54 0 проведены касательные AC и BC. Найдите угол
ACB. Ответ дайте в градусах.


   , если sin   0,6 и   1,5 ; 2  .
2

В8. На рисунке изображен график функции y  f x  и отмечены точки -2, -1, 1, 3. В какой из
В7. Найдите 8 sin 
этих точек значение производной наименьшее? В ответе укажите эту точку.
В9. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину).
Центр сферы находится в центре основания конуса. Образующая конуса равна 31 2 . Найдите
радиус сферы.
В10. Вероятность того, что батарейка бракованная, равна 0,04. Покупатель в магазине выбирает
случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки
окажутся исправными.
В11. Площадь поверхности тетраэдра равна 1,2. Найдите площадь поверхности многогранника,
вершинами которого являются середины ребер данного тетраэдра.
В12.
В13. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально
противоположных точек круговой трассы, длина которой равна 22 км. Через сколько минут
мотоциклисты поравняются в первый раз, если скорость одного из них на 20 км/ч больше скорости
другого?
В14.
Часть 2
Задания второй части выполняются с подробным решением и записью ответа.
 3

 x   3 cos x ; б) Найдите все корни этого уравнения,
С1. а) Решите уравнение 2 sin 2 
 2

 7

принадлежащие промежутку 
;2  .
 2

С2. Основанием прямой призмы ABCA1 B1C1 является равнобедренный треугольник
ABC , AB  AC  5, BC  8 . Высота призмы равна 3. Найдите угол между прямой A1 B и
плоскостью BCC1 .
С3.
С4. Прямая касается окружностей радиусов R и r в точках A и B. Известно, что расстояние между
центрами равно a причем r  R и r  R  a . Найдите AB.
C5. Найдите все значения a , при каждом из которых наименьшее значение функции
f x   4 x 2  4ax  a 2  2a  2 на множестве x  1 не меньше 6.
С6. Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записываю на 8 карточках. Карточки
переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из
чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные
восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант 2
Часть 1
Ответом в заданиях первой части является целое число или конечная десятичная дробь
В1. Держатели дисконтной карты книжного магазина получают при покупке скидку 2%. Книга
стоит 200 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
В2. На диаграмме показано распределение выплавки меди в 11 странах мира (в тысячах тонн) за
2006 год. Среди представленных стран первое место по выплавке меди занимала Папуа–Новая
Гвинея, одиннадцатое место — Индия. Какое место занимала Болгария?
В3. Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1
см  1 см (см. рис.). В ответе запишите
S

.
В4. Для того, чтобы связать свитер, хозяйке нужно 600 граммов шерстяной пряжи синего цвета.
Можно купить синюю пряжу по цене 70 рублей за 100 граммов, а можно купить неокрашенную
пряжу по цене 60 рублей за 100 граммов и окрасить её. Один пакетик краски стоит 40 рублей и
рассчитан на окраску 300 граммов пряжи. Какой вариант покупки дешевле? В ответ напишите,
сколько рублей будет стоить эта покупка.
log 3 x  2 
 7.
В5. Решите уравнение 3 2 7
В6. Через концы A, B дуги окружности в 112 0 проведены касательные AC и BC. Найдите угол
ACB. Ответ дайте в градусах.
7


   , если cos    и    ; 1,5  .
25
2

В8. На рисунке изображен график функции y  f x  и отмечены точки -2, -1, 1, 3. В какой из этих
В7. Найдите 25 cos
точек значение производной наибольшее? В ответе укажите эту точку.
В9. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину).
Центр сферы находится в центре основания конуса. Радиус сферы равен 15 2 . Найдите
образующую конуса.
В10. Вероятность того, что батарейка бракованная, равна 0,03. Покупатель в магазине выбирает
случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки
окажутся исправными.
В11. Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются
середины ребер данного тетраэдра.
В12.
В13. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально
противоположных точек круговой трассы, длина которой равна 19 км. Через сколько минут
мотоциклисты поравняются в первый раз, если скорость одного из них на 15 км/ч больше скорости
другого?
В14.
Часть 2
Задания второй части выполняются с подробным решением и записью ответа.
sin x
 1 
 7 2 sin 2 x ; б) Найдите все корни этого уравнения,

 49 
 3

принадлежащие промежутку  ;3  .
 2

С2. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 все ребра которой равны 1
найдите расстояние от точки B до прямой E1 F1 .
С1. а) Решите уравнение 
С3. Решите систему неравенств
С4. Четырехугольник ABCD описан около окружности и вписан в другую окружность. Прямые
AD и BC пересекаются в точке M. Найдите периметр треугольника ABM , если известно, что
AB  a и CD  b .
С5. Найдите все положительные значения a , при каждом из которых множеством решений
неравенства
является некоторый луч
С6. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них
мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более
2
от общего
11
числа учащихся группы, посетивших театр, а в кино мальчиков было не более
2
от общего числа
5
учащихся группы, посетивших кино.
а) Могло ли быть в группе 9 мальчиков, если дополнительно известно, что всего в группе было 20
учащихся?
б) Какое наибольшее количество мальчиков МОГЛО быть в группе, если дополнительно известно,
что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без
дополнительного условия пунктов а и б?
Вариант 3
Часть 1
Ответом в заданиях первой части является целое число или конечная десятичная дробь
В1. Держатели дисконтной карты книжного магазина получают при покупке скидку 4%. Книга
стоит 150 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
В2. На диаграмме показано распределение выплавки меди в 10 странах мира (в тысячах тонн) за
2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое
место — Казахстан. Какое место занимала Перу?
В3. Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1
см  1 см (см. рис.). В ответе запишите
S

.
В4. Для того, чтобы связать свитер, хозяйке нужно 600 граммов шерстяной пряжи синего цвета.
Можно купить синюю пряжу по цене 60 рублей за 100 граммов, а можно купить неокрашенную
пряжу по цене 50 рублей за 100 граммов и окрасить её. Один пакетик краски стоит 40 рублей и
рассчитан на окраску 300 граммов пряжи. Какой вариант покупки дешевле? В ответ напишите,
сколько рублей будет стоить эта покупка.
log 3 x 3 
 3.
В5. Решите уравнение 2 16
В6. Через концы A, B дуги окружности в 40 0 проведены касательные AC и BC. Найдите угол
ACB. Ответ дайте в градусах.


   , если sin   0,28 и    ; 1,5  .
2

В8. На рисунке изображен график функции y  f x  и отмечены точки -2, -1, 3, 4. В какой из этих
В7. Найдите 3 sin 
точек значение производной наименьшее? В ответе укажите эту точку.
В9. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину).
Центр сферы находится в центре основания конуса. Образующая конуса равна 52 2 . Найдите
радиус сферы.
В10. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает
случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки
окажутся исправными.
В11. Площадь поверхности тетраэдра равна 1,4. Найдите площадь поверхности многогранника,
вершинами которого являются середины ребер данного тетраэдра.
В12.
В13. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально
противоположных точек круговой трассы, длина которой равна 6 км. Через сколько минут
мотоциклисты поравняются в первый раз, если скорость одного из них на 18 км/ч больше скорости
другого?
В14.
Часть 2
Задания второй части выполняются с подробным решением и записью ответа.
 3

 x   3 cos x ; б) Найдите все корни этого уравнения,
 2

 7

;2  .
принадлежащие промежутку 
 2

С2. Основанием прямой призмы ABCA1 B1C1 является равнобедренный треугольник
ABC , AB  AC  5, BC  8 . Высота призмы равна 3. Найдите угол между прямой A1 B и
плоскостью BCC1 .
С1. а) Решите уравнение 2 sin 2 
С3.
С4. Прямая касается окружностей радиусов R и r в точках A и B. Известно, что расстояние между
центрами равно a причем r  R и r  R  a . Найдите AB.
C5. Найдите все значения a , при каждом из которых наименьшее значение функции
f x   4 x 2  4ax  a 2  2a  2 на множестве x  1 не меньше 6.
С6. Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записываю на 8 карточках. Карточки
переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из
чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные
восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться
Вариант 4
Часть 1
Ответом в заданиях первой части является целое число или конечная десятичная дробь
В1. Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга
стоит 240 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
В2. На диаграмме показано распределение выплавки меди в 11 странах мира (в тысячах тонн) за
2006 год. Среди представленных стран первое место по выплавке меди занимала Папуа–Новая
Гвинея, одиннадцатое место — Индия. Какое место занимал Лаос?
В3. Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1
см  1 см (см. рис.). В ответе запишите
S

.
В4. Для того, чтобы связать свитер, хозяйке нужно 800 граммов шерстяной пряжи синего цвета.
Можно купить синюю пряжу по цене 70 рублей за 100 граммов, а можно купить неокрашенную
пряжу по цене 60 рублей за 100 граммов и окрасить её. Один пакетик краски стоит 50 рублей и
рассчитан на окраску 400 граммов пряжи. Какой вариант покупки дешевле? В ответ напишите,
сколько рублей будет стоить эта покупка.
log815 x 3 
 6.
В5. Решите уравнение 3
В6. Через концы A, B дуги окружности в 116 0 проведены касательные AC и BC. Найдите угол
ACB. Ответ дайте в градусах.
4
 3

   , если cos    и   0,5 ;   .
5
 2

В8. На рисунке изображен график функции y  f x  и отмечены точки -2, -1, 2, 4. В какой из этих
В7. Найдите 4 cos
точек значение производной наибольшее? В ответе укажите эту точку.
В9. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину).
Центр сферы находится в центре основания конуса. Радиус сферы равен 19 2 . Найдите
образующую конуса.
В10. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает
случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки
окажутся исправными.
В11. Объем тетраэдра равен 2,1. Найдите объем многогранника, вершинами которого являются
середины ребер данного тетраэдра.
В12.
В13. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально
противоположных точек круговой трассы, длина которой равна 40 км. Через сколько минут
мотоциклисты поравняются в первый раз, если скорость одного из них на 25 км/ч больше скорости
другого?
В14.
Часть 2
Задания второй части выполняются с подробным решением и записью ответа.
sin x
 1 
 7 2 sin 2 x ; б) Найдите все корни этого уравнения,

 49 
 3

принадлежащие промежутку  ;3  .
 2

С2. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 все ребра которой равны 1
найдите расстояние от точки B до прямой E1 F1 .
С1. а) Решите уравнение 
С3. Решите систему неравенств
С4. Четырехугольник ABCD описан около окружности и вписан в другую окружность. Прямые
AD и BC пересекаются в точке M. Найдите периметр треугольника ABM , если известно, что
AB  a и CD  b .
С5. Найдите все положительные значения a , при каждом из которых множеством решений
неравенства
является некоторый луч
С6. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них
мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более
числа учащихся группы, посетивших театр, а в кино мальчиков было не более
2
от общего
11
2
от общего числа
5
учащихся группы, посетивших кино.
а) Могло ли быть в группе 9 мальчиков, если дополнительно известно, что всего в группе было 20
учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно,
что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без
дополнительного условия пунктов а и б?
Ответы и критерии оценивания заданий части 2.
Ответы к заданиям части 2:
Задание
С1
Вариант 1 и 3
a)

2
 k ; 

6
Вариант 2 и 4
 2k
a ) k ; 
7 5 13
;
;
2
2
6
arctg 0,6
 ;1;   1 ;0; 5;  
 3 
b) 2 ;
b) 
С2
С3
8
;3
3
2
 2;0; 0;3
С4
a 2  R  r  ; a 2  R  r 
С5
С6
a  0; a  2
а) нет; б) нет; в) 4
2
2
 2k
3
2
2a 2 2ab
;
ab ba
a 1
а) да; б) 9; в)
9
17
Критерии оценивания:
Критерии оценивания выполнения задания С1
Обоснованно получены верные ответы в п. а) и в п. б)
Обоснованно получен верный ответ в п. а), но обоснование отбора
корней в п. б) не приведено, или задача в п. а) обоснованно сведена к
исследованию простейших тригонометрических уравнений без
предъявления верного ответа, а п. б) приведен обоснованный набор
корней
Решение не соответствует ни одному из критериев, перечисленных выше
Баллы
2
1
0
Критерии оценивания выполнения задания С2
Обоснованно получен верный ответ
Решение содержит обоснованный переход к планиметрической задаче, но
получен неверный ответ или решение не закончено
Решение не соответствует ни одному из критериев, перечисленных выше
Критерии оценивания выполнения задания С3
Обоснованно получен верный ответ
- Верно решены оба неравенства системы, но неверно найдено общее
решение
- допущена вычислительная ошибка или описка
Обоснованно получен верный ответ в одном из неравенств системы
Решение не соответствует ни одному из критериев, перечисленных выше
Критерии оценивания выполнения задания С4
Рассмотрены все возможные геометрические конфигурации, и получен
правильный ответ
Рассмотрена хотя бы одна возможная конфигурация, для которой
получено правильное значение искомой величины или рассмотрены все
возможные геометрические конфигурации, но получен неправильный
ответ из-за одной арифметической ошибки
Рассмотрена хотя бы одна возможная геометрическая конфигурация, в
которой получено значение искомой величины, неправильное из-за
арифметической ошибки
Решение не соответствует ни одному из критериев, перечисленных выше
Критерии оценивания выполнения задания С5
Обоснованно получен верный ответ. .
Рассмотрены все возможные случаи. Получен верный ответ, но решение
либо содержит пробелы, либо вычислительную ошибку или описку.
Рассмотрены все возможные случаи. Получен ответ, но решение
содержит ошибки
2
1
0
3
2
1
0
3
2
1
0
Баллы
4
3
2
Рассмотрены некоторые случаи. Для рассмотренных случаев получен
ответ, возможно неверный из-за ошибок
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Критерии оценивания выполнения задания С6
Баллы
Верно выполнены все 3 пункта: а), б) и в)
4
Выполнены все три пункта, однако в одном из пунктов ответ недостаточно
3
обоснован или неверен вследствие арифметической ошибки
Верно выполнены пункты а) и б), либо верно выполнен пункт в)
2
Верно выполнен один из 2-х пунктов: а) или б)
1
Решение не соответствует ни одному из критериев, перечисленных выше
0