вариант 3x

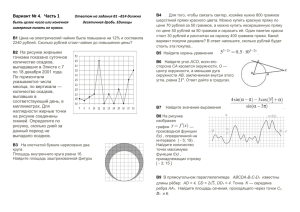
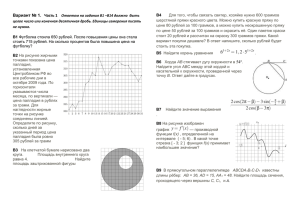
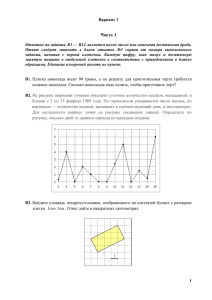
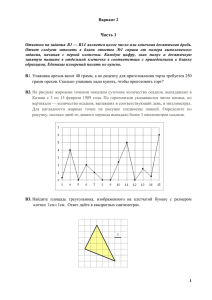
Вариант № 3. Часть 1 Ответом на задания В1 –В14 должно быть
целое число или конечная десятичная дробь. Единицы измерения писать
не нужно.
B1 Цена на электрический чайник была повышена на 17% и составила
1755 рублей. Сколько рублей стоил чайник до повышения цены?
B2 На рисунке жирными
точками показано
суточное количество
осадков, выпадавших в
Мурманске с 7 по 22
ноября 1995 года. По
горизонтали
указываются числа
месяца, по вертикали —
количество осадков,
выпавших в этот день, в
миллиметрах. Для
наглядности жирные
точки на рисунке
соединены линией.
Определите по рисунку,
сколько дней за данный
период не выпадало
осадков.
B3 На клетчатой бумаге нарисовано два круга.
Площадь внутреннего круга равна 9.
Найдите площадь заштрихованной фигуры
B4
Для того, чтобы связать свитер, хозяйке нужно 900 граммов
шерстяной пряжи красного цвета. Можно купить красную пряжу по
цене 60 рублей за 50 граммов, а можно купить неокрашенную пряжу
по цене 50 рублей за 50 граммов и окрасить её. Один пакетик краски
стоит 30 рублей и рассчитан на окраску 450 граммов пряжи. Какой
вариант покупки дешевле? В ответ напишите, сколько рублей будет
стоить эта покупка.
B5 Найдите корень уравнения
.
B6 Найдите угол ACO, если его
сторона CA касается окружности, O —
центр окружности, а меньшая дуга
окружности AB, заключенная внутри этого
угла, равна 38о. Ответ дайте в градусах.
B7
Найдите значение выражения
B8 На рисунке изображен
график
—
производной функции
f(x) , определенной на
интервале ( - 4;16) . В
какой точке отрезка
[0;13] функция f(x)
принимает наибольшее
значение?
B9 В прямоугольном параллелепипеде ABCDA1B1C1D1 известны
длины рёбер: CD = 4, BC = 2√5, CC1 = 4. Точка K — середина
ребра DD1. Найдите площадь сечения, проходящего через точки C1,
B1 и K.
B10 B кармане у Коли было четыре конфеты — «Грильяж»,
«Ласточка», «Взлётная» и «Василёк», а так же ключи от квартиры.
Вынимая ключи, Коля случайно выронил из кармана одну конфету.
Найдите вероятность того, что потерялась конфета «Ласточка».
С1 а) Решите уравнение 5 sin 2x = 11 ( sin x + cos x ) - 7;
б) Найдите корни этого уравнения, принадлежащие промежутку [0;π].
С2 Дан куб ABCDA1B1C1D1 с ребром 1. Найдите расстояние от точки
А до плоскости A1 BТ, где Т - середина отрезка AD.
B11 В сосуде, имеющем форму конуса,
2
уровень жидкости достигает высоты.
3
Объём жидкости равен 152 мл. Сколько
миллилитров жидкости нужно долить,
чтобы наполнить сосуд полностью?
С3 Решите систему неравенств:
B12 Для получения на экране увеличенного изображения лампочки в
лаборатории используется собирающая линза с главным фокусным
расстоянием f = 75 см. Расстояние d1 от линзы до лампочки может
изменяться в пределах от 250 до 350 см, а расстояние d2 от линзы до
экрана — в пределах от 80 до 100 см. Изображение на экране будет
четким, если выполнено соотношение
. Укажите, на
каком наименьшем расстоянии от линзы можно поместить лампочку,
чтобы еe изображение на экране было четким. Ответ выразите в
сантиметрах.
B13 Расстояние между пристанями A и B равно 192 км. Из A в B по
течению реки отправился плот, а через 3 часа вслед за ним
отправилась яхта, которая, прибыв в пункт B, тотчас повернула
обратно и возвратилась в A. К этому времени плот прошел 92 км.
Найдите скорость яхты в неподвижной воде, если скорость течения
реки равна 4 км/ч. Ответ дайте в км/ч.
B14 Найдите точку минимума функции
y = ( x 2 - 15x + 15 ) e 3 - x
Часть 2
Для записи решений и ответов на задания С1- С6
используйте бланк ответов №2. Запишите сначала номер
выполняемого задания , а затем полное обоснованное решение и ответ.
С4 Прямая отсекает от сторон прямого угла отрезки 3 и 4. Найдите
радиус окружности, касающейся этой прямой и сторон угла
С5 Найдите все значения a, при каждом из которых наименьшее
значение функции f(x)=x2 - 4ax+5a² на множестве, заданном
неравенством | х │≤ 6, больше 8.
С6 На доске записаны два числа 540 и 450.За один ход можно
записать натуральное число, равное либо среднему
арифметическому любых двух чисел, уже записанных на доске ,
либо модулю разности любых двух чисел ,уже записанных на доске.
а) Можно ли за несколько ходов получить на доске 315?
б) Можно ли за несколько ходов получить на доске 120?
в) Какое наименьшее натуральное число можно получить на доске?