doc - Математика. Теоретическая механика

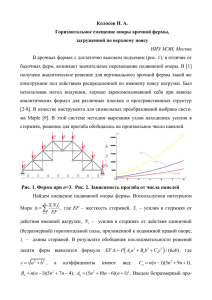
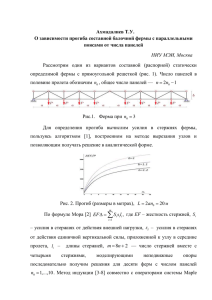
Загребин М. С.
Прогиб составной фермы под действием равномерной нагрузки
НИУ МЭИ, Москва
В [1] найдено точное решение для прогиба составной балочной фермы с
крестообразной
решеткой
под
действием
сосредоточенной
силы
в
сочленяющем шарнире. Рассмотрим аналогичную ферму, загруженную
равномерно по верхнему поясу (рис. 1). Найдем ее прогиб как функцию
размеров и числа панелей фермы.
Рис. 1. Ферма, n=3
Последнее есть наиболее трудная часть задачи, выполнить которую
можно, в значительной мере прибегая к помощи какой-либо системе
символьной математики, в частности Maple [2]. При этом потребуется
составлять и решать рекуррентные уравнения метода индукции, развитого в
работах [3-5] для задач о прогибе ферм и для задачи об осадке свайного
фундамента [6]. Последовательный расчет с использованием интеграла Мора
(или, что то же, формулы Максвелла-Мора) дал следующий результат:
,
где
,
,
,
. Если построить соответствующие
кривые (рис. 2), то можно заметить интересное пересечение кривых прогиба
для различных высот фермы (b – в метрах, прогиб отнесен к EF/P, длина
пролета постоянна L  2a(n  1) ). Получается таким образом, что фермы разной
высоты при некотором значении числа панелей (здесь – 6) имеют одинаковую
жесткость. Экстремум (минимум) прогиба практически не заметен. Рост же
кривых имеет кубический характер. Выясняется это из предела lim  / n3  b .
n
Литература
1. Шикин К.С., Китаев С.С. Деформация составной балочной фермы
шпренгельного типа // Актуальные вопросы образования и науки.
Сборник научных трудов по материалам Международной научнопрактической конференции 30 сентября 2014 г. Часть 7. с. 154-155.
2. Кирсанов М. Н. Решебник. Теоретическая механика / Под ред. А. И.
Кириллова. М.: Физматлит, 2008 г. 384 с.
3. Кирсанов М.Н. Скрытая особенность и асимптотические свойства одной
плоской балочной фермы // Строительная механика и расчет сооружений.
2014. №4. С. 9-12.
4. Кирсанов М.Н. Статический расчет и анализ пространственной
стержневой системы // Инженерно-строительный журнал. 2011. №6 (24).
С. 28-34.
5. Кирсанов
М.Н.
Анализ
прогиба
фермы
прямоугольного
пространственного покрытия // Инженерно-строительный журнал. 2015.
№ 1 (53). С. 32-38.
6. Кирсанов М.Н. Дискретная модель свайного фундамента // Инженерностроительный журнал. 2015. №3 (55). С. 3–9.