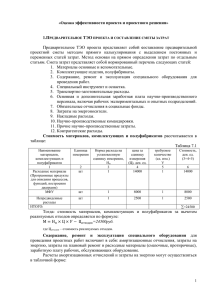
оценка величины R t

А. И. Богданов, Ф. В. Ильин
Санкт-Петербургский государственный университет технологии и дизайна,
г. Санкт-Петербург
ОЦЕНКА ЭФФЕКТИВНОСТИ И ПРИНЯТИЕ
ИНВЕСТИЦИОННЫХ РЕШЕНИЙ В УСЛОВИЯХ РИСКА
Ключевые слова: инвестиции, оценка эффективности, принятие
решений, математическая модель, случайная величина, закон распределения.
При анализе эффективности инвестиций на практике широко
применяется показатель чистой приведенной (текущей) стоимости - Net
Present Value (NPV) [1].
T
Пt
Zt
NPV  


t
t
t 1 (1  r )
t 1 (1  r )
T
,
(1)
где NPV - чистый приведенный доход;
Zt - величина инвестиций в t-ом году;
Пt - генерируемые за счет сделанных инвестиций доходы в t-ом году;
r - коэффициент дисконтирования;
T - количество лет жизненного цикла изделия.
Отметим, что формулу (1) можно преобразовать к виду
T
NPV  
t 1
Rt
,
(1  r ) t
(2)
где 𝑅𝑡 = П𝑡 − 𝑍𝑡 – прибыль, получаемая за счет сделанных инвестиций в t-ом
году.
Положительное значение NPV означает, что по результатам реализации
проекта расходы на инвестированный капитал будут покрыты денежным
потоком, генерируемым проектом. Соответственно, при сравнении нескольких
проектов с сопоставимыми объемными показателями инвестирования и
денежного потока, предпочтительным будет тот, NPV которого больше.
Заметим, что модели (1) и (2) являются детерминистическими и не
учитывают вероятностный характер будущих доходов и затрат, связанный с
наличием многочисленных рисков и неопределенностей.
На самом деле значение Rt представляет собой непрерывную случайную
величину. Из этого вытекает, что NPV как сумма случайных величин также
является случайной величиной.
В настоящей статье рассмотрим случай задания постоянной нормы
дисконта r. В этом случае при нормальном законе распределения случайных
величин Rt чистый дисконтированный доход NPV представляет собой сумму
нормально распределенных случайных величин, и вследствие этого также
имеет нормальный закон распределения. Его характеристики – математическое
ожидание и дисперсия могут быть рассчитаны следующим образом
T
 Rt  T
Rt  T
1
M NPV   М 

M

 M Rt 



t
t
t






1

r
1

r
1

r
 t 1
 t 1 
 t 1
T
Rt  T 2  Rt  T 1 T
Rt
Rl
 NPV    



2
cov(
,
)






t
t
l
t
(
1

r
)
(
1

r
)




1

r
1

r
t

1
t

1
t

1
l

t

1




2
2
𝑇
𝑇−1
𝑇
1
1
2 (𝑅 )
=∑
𝜎
+
2
𝑐𝑜𝑣(𝑅𝑡 , 𝑅𝑙 )
∑
∑
𝑡
(1 + 𝑟)2𝑡
(1 + 𝑟)𝑡+𝑙
𝑡=1
(3)
𝑡=1 𝑙=𝑡+1
где 𝑐𝑜𝑣(𝑅𝑡 , 𝑅𝑙 )- ковариация случайных величин 𝑅𝑡 и 𝑅𝑙 .
Оценки величин Rt на будущее с учетом жизненного цикла изделия могут
быть получены экспертами. При этом каждый эксперт дает как бы одну из
возможных реализаций случайного процесса во времени.
Усредняя
экспертные оценки для всех t, получим оценку математическое ожидание
дохода M(Rt) и дисперсии σ2(Rt) (характеристики разброса ее значений
относительно математического ожидания).
Оценка математического ожидания Rt с учетом мнений всех экспертов
∑𝑚
𝑗=1 𝑅𝑡𝑗
̅
𝑅𝑡 =
,
𝑚
где m – количество экспертов;
𝑅𝑡𝑗 - оценка величины Rt j-м экспертом.
Если предположить, что все эксперты дают несмещенные оценки
величины M(Rt), т.е. 𝑀(𝑅𝑡𝑗 ) = 𝑀(𝑅𝑡 ), то
𝑚
1
1
𝑀(𝑅̅𝑡 ) = ∑ 𝑀(𝑅𝑡𝑗 ) = 𝑚𝑀(𝑅𝑡 ) = 𝑀(𝑅𝑡 ).
𝑚
𝑚
𝑗=1
Таким образом, оценка 𝑅̅𝑡 является несмещенной.
Оценки дисперсий 𝑅𝑡 и ковариаций 𝑅𝑡 и 𝑅𝑙 могут быть получены на
основании обработки результатов экспертных оценок
𝑚
1
𝜎̂ 2 (𝑅𝑡 ) =
∑(𝑅𝑡𝑗 − 𝑅̅𝑡 )2
𝑚−1
𝑚
𝑐𝑜𝑣
̂ (𝑅𝑡 , 𝑅𝑙 ) =
𝑗=1
1
∑(𝑅𝑡𝑗 − 𝑅̅𝑡 )(𝑅𝑙𝑗 − 𝑅̅𝑙 )
𝑚−1
𝑗=1
Подставляя в выражение (3) вместо неизвестных параметров их оценки,
получим оценку математического ожидания и дисперсии случайной величины
NPV
𝑇
̅̅̅̅̅̅ = ∑
𝑁𝑃𝑉
𝑡=1
1
𝑅̅
(1 + 𝑟)𝑡 𝑡
(4)
𝑇
𝜎̂ 2 (𝑁𝑃𝑉) = ∑
𝑡=1
𝑇−1
𝑇
1
1
2 (𝑅 )
𝜎
̂
+
2
𝑐𝑜𝑣
̂ (𝑅𝑡 , 𝑅𝑙 )
∑
∑
𝑡
(1 + 𝑟)2𝑡
(1 + 𝑟)𝑡+𝑙
𝑡=1 𝑙=𝑡+1
̅̅̅̅̅̅) = 𝑀(𝑁𝑃𝑉), т.е. полученная оценка
При этом легко видеть, что 𝑀(𝑁𝑃𝑉
математического ожидания 𝑁𝑃𝑉 является несмещенной.
В
стохастической
постановке
задача
выбора
оптимального
инвестиционного проекта представляет собой задачу выбора из множества
вероятностных распределений. Согласно современной портфельной теории
для инвестора важны прежде всего математическое ожидание и дисперсия
ожидаемого результата [2]. Таким образом, мы имеем многокритериальную
задачу – максимизация математического ожидания 𝑁𝑃𝑉 и минимизация его
дисперсии [3].
Для каждого варианта инвестиционного проекта оценки этих параметров
закона распределения 𝑁𝑃𝑉могут быть найдены по формулам (4),
Для решения упомянутой многокритериальной задачи воспользуемся
методом сведения целей в ограничения. На изменчивость возможного
результата наложим ограничение, а из удовлетворяющих этому ограничению
вариантов выбираем тот, у которого значение M(NPV) больше.
Результаты практической апробации в ЗАО «АНА» (Санкт-Петербург)
подтверждают
эффективность
предложенного
подхода
к
оценке
эффективности инвестиций и принятию инвестиционных решений в условиях
риска.
Работа поддержана грантом Комитета по науке и высшей школе при
правительстве Санкт-Петербурга.
Литература
1. Михайлова Э.А., Орлова Л.Н. Экономическая оценка инвестиций:
Учебное пособие.- Рыбинск: РГАТА, 2008.- 176 с.
2. Шарп, У. Инвестиции/ пер. с англ. Г. Александер, Бэйли Дж.- М.:
ИНФРА-М, 1997.- 1024 с.
3. Богданов А.И. Методы и модели принятия инвестиционных решений:
монография./ А.И. Богданов, Л.Н.Никитина – СПб.: СПГУТД, 2009.87 с.