Аксиомы стереометрии
реклама
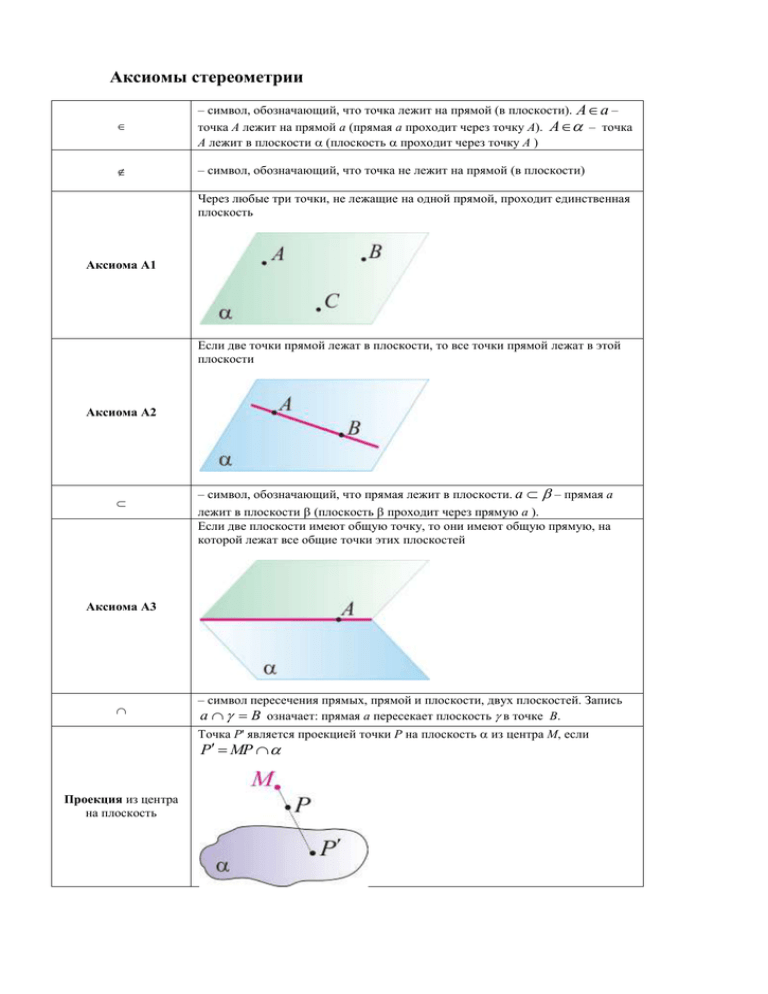
Аксиомы стереометрии – символ, обозначающий, что точка лежит на прямой (в плоскости). A a – точка A лежит на прямой a (прямая a проходит через точку A). A – точка A лежит в плоскости (плоскость проходит через точку A ) – символ, обозначающий, что точка не лежит на прямой (в плоскости) Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость Аксиома А1 Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости Аксиома А2 – символ, обозначающий, что прямая лежит в плоскости. a – прямая a лежит в плоскости (плоскость проходит через прямую a ). Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей Аксиома А3 – символ пересечения прямых, прямой и плоскости, двух плоскостей. Запись а В означает: прямая a пересекает плоскость в точке B. Точка P' является проекцией точки P на плоскость из центра M, если P MP Проекция из центра на плоскость Свойства треугольника, образованного диагоналями граней куба ΔAB1D1 – равносторонний, AB1=AD1=B1D1= a 2 (a – длина ребра куба), его медиана AO= a 6 . 2 В правильной четырёхугольной пирамиде, длины всех рёбер которой равны, несмежные боковые рёбра взаимно перпендикулярны. Свойство правильной четырёхугольной пирамиды, все рёбра которой равны Через прямую и не лежащую на ней точку проходит единственная плоскость Следствие 1 из аксиом стереометрии Через две пересекающиеся прямые проходит единственная плоскость Следствие 2 из аксиом стереометрии











