m=1 кг

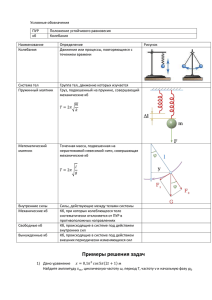
7475. Найти период малых колебаний системы, состоящей из жесткой
невесомой штанги, верхний конец которой закреплен на шарнире, и двух
грузов малых размеров массами m=1 кг и M= 2 кг, закрепленных на
штанге на расстояниях r =0,5 м и R=1 м от шарнира. Трением
пренебречь, g = 10 м/c2.
Дано: m=1 кг; M= 2 кг; r =0,5 м; R=1 м; g = 10 м/c2.
Найти: T=?
Решение. Применим для решения этой задачи следующий прием. Представим себе,
что изображенный на рисунке маятник вывели из положения равновесия, сообщив ему
некоторую суммарную энергию E0 так, что в результате начались колебания системы с
малой амплитудой. Пусть в некоторый момент времени нижний груз оказался
смещенным из положения равновесия на малую величину х и двигался в этот момент
со скоростью v. Тогда угол, который составляет в этот момент штанга с вертикалью,
равен α = x/R. При этом смещение верхнего груза из положения равновесия равно
𝑟
𝑠 = 𝑟 ∙ 𝛼 = ∙ 𝑥,
𝑅
а его скорость равна
𝑟
𝑢 = ∙ 𝑣.
𝑅
Кинетическая энергия маятника в рассматриваемый момент времени равна сумме
кинетических энергий нижнего и верхнего грузов:
𝑀 ∙ 𝑣 2 𝑚 ∙ 𝑢2 𝑀 ∙ 𝑣 2 𝑚 ∙ 𝑟 2 2
𝑣2
𝑊=
+
=
+
∙𝑣 =
∙ (𝑀 ∙ 𝑅2 + 𝑚 ∙ 𝑟 2 ).
2
2
2
2
2
2∙𝑅
2∙𝑅
Потенциальная энергия системы в этот момент складывается из потенциальных
энергий взаимодействия грузов с Землей:
𝑈 = 𝑀 ∙ 𝑔 ∙ 𝑅 ∙ (1 − cos 𝛼) + 𝑚 ∙ 𝑔 ∙ 𝑟 ∙ (1 − cos 𝛼).
При записи этого выражения мы считали, что U= 0 в положении равновесия системы.
Так как угол отклонения штанги от вертикали мал (α<<1 рад), то для вычисления
косинуса можно воспользоваться приближенной формулой:
𝛼2
cos 𝛼 ≈ 1 − .
2
Тогда
𝑈 = 𝑀 ∙ 𝑔 ∙ 𝑅 ∙ (1 − cos 𝛼) + 𝑚 ∙ 𝑔 ∙ 𝑟 ∙ (1 − cos 𝛼) ≈
𝑀 ∙ 𝑔 ∙ 𝑅 2 𝑚 ∙ 𝑔 ∙ 𝑟 2 𝑔 ∙ 𝑥2
≈
∙𝛼 +
∙𝛼 =
∙ (𝑀 ∙ 𝑅 + 𝑚 ∙ 𝑟).
2
2
2 ∙ 𝑅2
Так как по условию задачи трения нет, то полная механическая энергия системы
сохраняется:
𝑣2
𝑔 ∙ 𝑥2
2
2
𝑊+𝑈=
∙ (𝑀 ∙ 𝑅 + 𝑚 ∙ 𝑟 ) +
∙ (𝑀 ∙ 𝑅 + 𝑚 ∙ 𝑟) = 𝐸0 = 𝑐𝑜𝑛𝑠𝑡.
2 ∙ 𝑅2
2 ∙ 𝑅2
Продифференцируем это уравнение по времени t, пользуясь правилом
дифференцирования сложной функции. Поскольку
𝑑 2
𝑑𝑣
𝑑𝑥 𝑑 2 𝑥
(𝑣 ) = 2 ∙ 𝑣 ∙
=2∙
∙
;
𝑑𝑡
𝑑𝑡
𝑑𝑡 𝑑𝑡 2
𝑑 2
𝑑𝑥
(𝑥 ) = 2 ∙ 𝑥 ∙
, то
𝑑𝑡
𝑑𝑡
𝑀 ∙ 𝑅2 + 𝑚 ∙ 𝑟 2
𝑑2𝑥 𝑔
∙ 𝑣 ∙ 2 + 2 ∙ (𝑀 ∙ 𝑅 + 𝑚 ∙ 𝑟) ∙ 𝑥 ∙ 𝑣 = 0.
𝑅2
𝑑𝑡
𝑅
Полученное уравнение можно переписать в виде:
𝑔 ∙ (𝑀 ∙ 𝑅 + 𝑚 ∙ 𝑟)
𝑥̈ +
∙ 𝑥 = 0.
𝑀 ∙ 𝑅2 + 𝑚 ∙ 𝑟 2
В результате получилось уравнение гармонических колебаний
𝑥̈ + 𝜔2 ∙ 𝑥 = 0.
с круговой частотой
𝑔 ∙ (𝑀 ∙ 𝑅 + 𝑚 ∙ 𝑟)
𝜔=√
.
𝑀 ∙ 𝑅2 + 𝑚 ∙ 𝑟 2
Следовательно, искомый период малых колебаний данной механической системы
равен
𝑇=
2∙𝜋
𝑀 ∙ 𝑅2 + 𝑚 ∙ 𝑟 2
=2∙𝜋∙√
.
𝜔
𝑔 ∙ (𝑀 ∙ 𝑅 + 𝑚 ∙ 𝑟)
2 ∙ 12 + 1 ∙ 0,52
𝑇 =2∙𝜋∙√
= 1,9 𝑐.
10 ∙ (2 ∙ 1 + 1 ∙ 0,5)
Ответ.
𝑴 ∙ 𝑹 𝟐 + 𝒎 ∙ 𝒓𝟐
𝑻=𝟐∙𝝅∙√
, 𝑻 = 𝟏, 𝟗 𝒄.
𝒈 ∙ (𝑴 ∙ 𝑹 + 𝒎 ∙ 𝒓)