Лекция №5 по прикладной математике

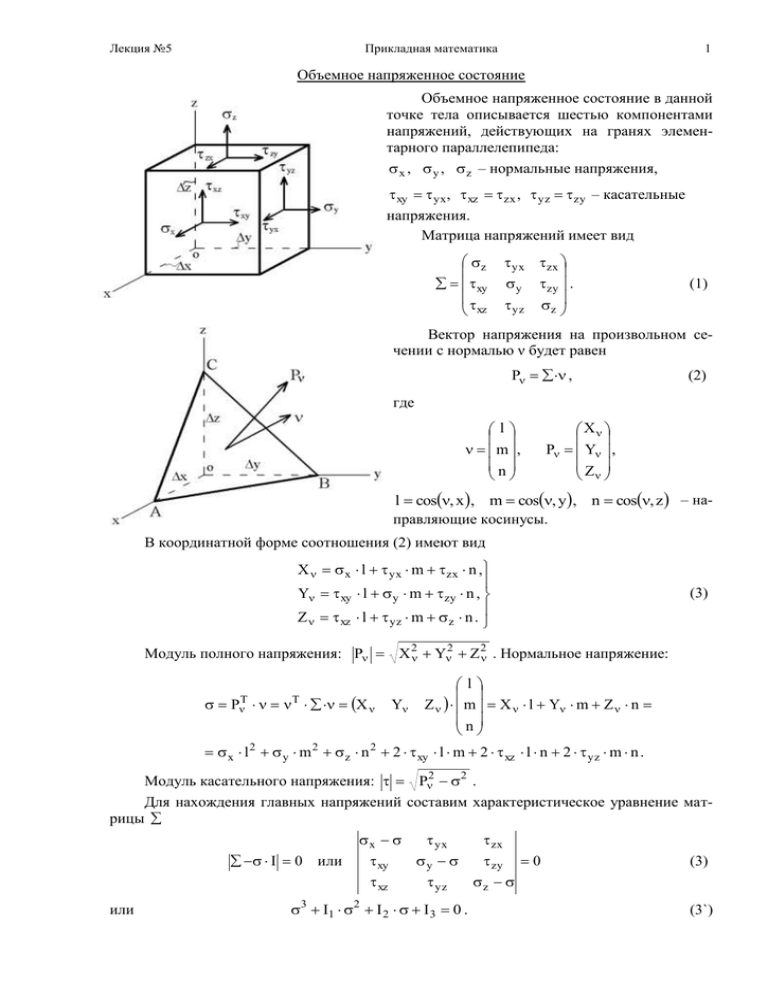
Лекция №5
Прикладная математика
1
Объемное напряженное состояние
Объемное напряженное состояние в данной
точке тела описывается шестью компонентами
напряжений, действующих на гранях элементарного параллелепипеда:
 x ,  y ,  z – нормальные напряжения,
 xy   yx ,  xz   zx ,  yz   zy – касательные
напряжения.
Матрица напряжений имеет вид
 z

    xy

 xz
 yx zx 

 y zy  .
 yz z 
(1)
Вектор напряжения на произвольном сечении с нормалью ν будет равен
P    ,
(2)
где
l
 
   m,
n
 
 X 
 
P   Y  ,
Z 
 
l  cos, x , m  cos, y, n  cos, z  – направляющие косинусы.
В координатной форме соотношения (2) имеют вид
X    x  l   yx  m   zx  n ,

Y   xy  l   y  m   zy  n , 

Z    xz  l   yz  m   z  n . 
(3)
Модуль полного напряжения: P  X 2  Y2  Z 2 . Нормальное напряжение:

PT
        X 
T
Y
l
 
Z     m   X   l  Y  m  Z   n 
n
 
  x  l 2   y  m 2   z  n 2  2   xy  l  m  2   xz  l  n  2   yz  m  n .
Модуль касательного напряжения:   P2  2 .
Для нахождения главных напряжений составим характеристическое уравнение матрицы 
   I  0 или
или
x  
 yx
 zx
 xy
y  
 zy
 xz
 yz
z  
3  I1  2  I 2    I 3  0 .
0
(3)
(3`)
Лекция №5
Прикладная математика
2
Здесь I1 , I 2 , I 3 – инварианты напряжений (их величина не зависит от ориентации
сечения, проведенного через точку О, так как главные напряжения и, следовательно, коэффициенты уравнения (3), корнями которого они являются, не зависят от ориентации сечения).
Раскрывая определитель (3), получим выражения для инвариантов I1 , I 2 , I 3 в произвольных осях координат Oxyz
I1    x   y   z ,

2
2
2
(4)
I 2   x   y   x   z   y   z   xy   xz   yz ,

2
2
2
I 3      x   y   z  2   xy   yz   xz   x   yz   y   xz   z   xy .
В главных осях (оси x, y, z направлены перпендикулярно главным сечениям, нормальные напряжения равны главным напряжениям, касательные напряжения равны нулю)
выражения (4) принимают вид


I1  1  2  3  , I 2  1  2  1  3  2  3 , I 3  1  2  3 .
(5)
Для нахождения главных напряжений необходимо решить кубическое уравнение
(3`). При этом обычно используются численные методы, например, метод Ньютона. Для
определения положения главных сечений воспользуемся равенством
(6)
 i  I  i  0 , i  1, 2, 3,
которое следует из определения собственных значений и собственных векторов матрицы.
Так как определитель системы линейных алгебраических уравнений (6) равен нулю
(см. (3)), то уравнения в (6) будут линейно зависимы (это, в частности, связано с тем, что
собственные векторы определены с точностью до постоянного множителя). Поэтому одно
из уравнений системы (6) заменим условием, чтобы длина собственных векторов равнялась единице. Получим следующую систему линейных алгебраических уравнений:
 x  i   l i   xy  m i   xz  n i  0 ,

 xy  l i   y   i  m i   zy  n i  0 ,  i  1 , 2 , 3

l i2  m i2  n i2  1.



(7)
Найдем решение системы (7). Пусть l i  0 , разделим все уравнения на l i


mi
ni
 x  i    yx    zx   0 ,
li
li


mi
ni
 xy   y   i 
  zy   0 , 
li
li


2
2
 m 
 ni  
2

i
      1.
l i  1  

  l i 
 l i  

mi
ni
 X1 ,
 X 2 , получим
Введем обозначения
li
li


 x  i    yx  X1  zx  X 2  0 ,



 xy   y  i  X1   zy  X 2  0 , 

li 
1
1  X12  X 22
.
(8)
(9)
(10)
Лекция №5
Прикладная математика
3
Решая систему уравнений (9), находим X1 и X2 . Подставляя найденные значения
X1 и X2 в соотношение (10) найдем l i и затем mi и n i из равенств
mi  X1  li , ni  X2  li .
Так как матрица ∑ симметричная, то ее собственные векторы
 l1 
 l2 
 l3 
 


 
1   m1  ,  2   m 2  ,  3   m 3 
n 
n 
n 
 1
 2
 3
будут взаимно ортогональны
1   2
1   3
2  3
 l1  l 2  m1  m 2  n1  n 2  0 , 

 l1  l 3  m1  m 3  n1  n 3  0 , 
 l 2  l 3  m 2  m 3  n 2  n 3  0 .

(11)
Соотношения (5) и (11) можно использовать для проверки правильности нахождения
собственных значений 1 , 2 , 3 (главных напряжений) и собственных векторов
1 ,  2 , 3 (положения главных сечений) матрицы напряжений.
Метод Ньютона решения нелинейных уравнений
Рассмотрим нелинейное уравнение
f ( x )  0.
(1)
Пусть x – уравнения (1). Тогда выполняется равенство
*
f ( x )  0.
(2)
*
Предположим, что известно приближенное значение корня, которое обозначим через
x 0 и назовем нулевым приближением. Разность между точным значением корня x и
*
приближенным значением x 0 обозначим через h
x  x0  h .
(3)
*
Отсюда получим
(4)
x  x0  h .
*
Подставим (4) в (2)
f x 0  h   0 .
(5)
Считая h малой величиной, разложим левую часть (5) в ряд Тейлора по степеням h в
точке x 0 :
f x 0  2
(6)
f x 0   f x 0   h 
 h    0.
2
Ограничившись в (6) первыми двумя членами, найдем
f x 0   f x 0   h  0 .
(7)
Отсюда
f x 0 
h
.
(8)
f x 0 
Подставляя(8) в (3), получим
f x 0 
x  x0  h  x0 
.
(9)
*
f x 0 
Правую часть (9) обозначим через x1 и назовем первым приближением к корню
f x 0 
x1  x 0 
.
(10)
f x 0 
Лекция №5
Прикладная математика
4
Рассуждая аналогично, получим
f x1 
,
f x1 
f x n 
x n 1  x n 
,
f x n 
Итерации прекращаем при выполнении условия
x n 1  x n   ,
x 2  x1 
(11)
(12)
(13)
где ε заданное число (например,   0,001), и полагаем x  x n 1 .
*
Окончательно алгоритм метода Ньютона можно описать так:
задаем x 0 – нулевое приближение, выполняем итерации по формуле
f x n 
x n 1  x n 
, n  0, 1, 2, 
(14)
f x n 
до выполнения условия (13).
При удачном выборе x 0 итерации сходятся очень быстро, при неудачном – итерации
могут расходиться.
Геометрическая интерпретация метода Ньютона
Задаем значение x 0 . В точке x 0 , f x 0  проводим
касательную к графику функции y  f x  до пересечения с осью x. Получаем точку x1 и т.д. Приведенный чертеж объясняет также, почему метод
Ньютона называют еще методом касательных.
Пример. Найти корень нелинейного уравнения
(15)
f x   ln x2  1  2  x  5  0 .
Для выбора нулевого приближения составим таблицу

x
f(x)
2
2.609
3
1.303

4
-0.167
Так как функция f(x) непрерывна и в точках x  3 и x  4 принимает значения разных знаков, то на интервале 3;4 она имеет корень. Поэтому полагаем x 0  3.5 . Имеем
далее
f x 0 
2x
ln 3.52  1  2  3.5  5
f x   2
 2 , x1  x 0 
 3.5 
 3.8968 ;
3.5
f x 0 
x 1
2 2
2
3.5  1
f x1 
f x 2 
x 2  x1 
 3.8905 ; x 3  x 2 
 3.8905 .
f x1 
f x 2 
Итерации сошлись. За корень уравнения (15) принимаем x  3.8905 . Для проверки
*
вычислим f x  :

*

f 3.8905  1.1  1013  0 .