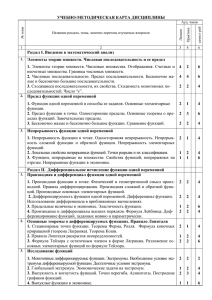
010500.62-01 Математический анализ

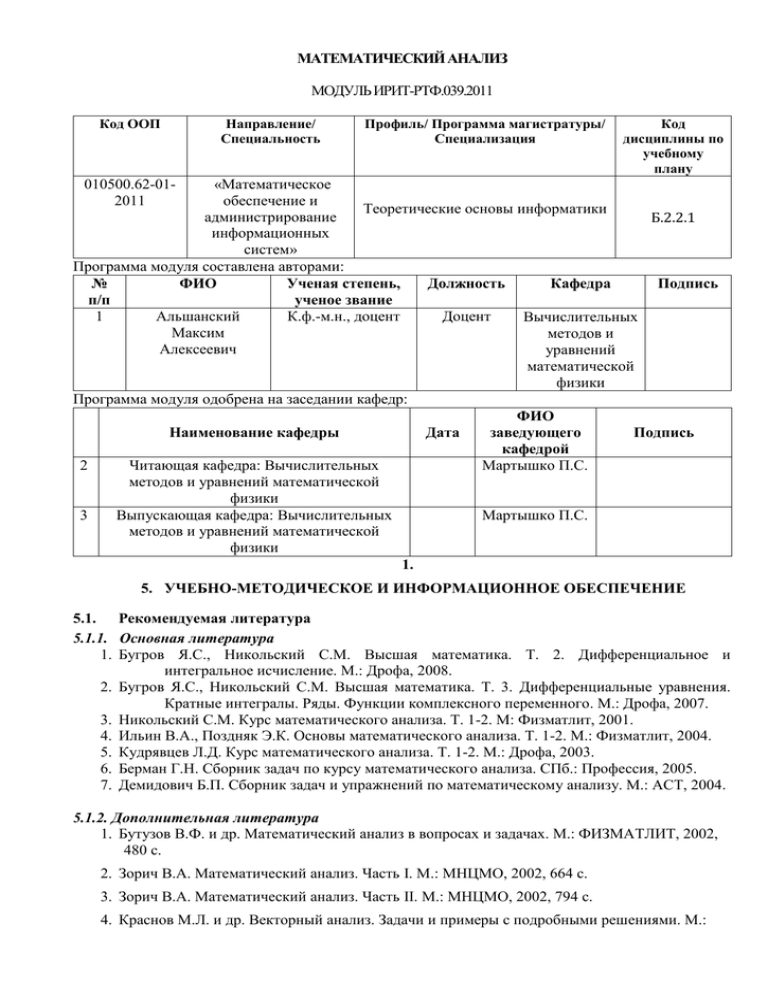
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
МОДУЛЬ ИРИТ-РТФ.039.2011
Код ООП
Направление/
Специальность
Профиль/ Программа магистратуры/
Специализация
Код
дисциплины по
учебному
плану
«Математическое
обеспечение и
Теоретические основы информатики
администрирование
Б.2.2.1
информационных
систем»
Программа модуля составлена авторами:
№
ФИО
Ученая степень,
Должность
Кафедра
Подпись
п/п
ученое звание
1
Альшанский
К.ф.-м.н., доцент
Доцент
Вычислительных
Максим
методов и
Алексеевич
уравнений
математической
физики
Программа модуля одобрена на заседании кафедр:
ФИО
Наименование кафедры
Дата
заведующего
Подпись
кафедрой
2
Читающая кафедра: Вычислительных
Мартышко П.С.
методов и уравнений математической
физики
3
Выпускающая кафедра: Вычислительных
Мартышко П.С.
методов и уравнений математической
физики
1.
010500.62-012011
5. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
5.1. Рекомендуемая литература
5.1.1. Основная литература
1. Бугров Я.С., Никольский С.М. Высшая математика. Т. 2. Дифференциальное и
интегральное исчисление. М.: Дрофа, 2008.
2. Бугров Я.С., Никольский С.М. Высшая математика. Т. 3. Дифференциальные уравнения.
Кратные интегралы. Ряды. Функции комплексного переменного. М.: Дрофа, 2007.
3. Никольский С.М. Курс математического анализа. Т. 1-2. М: Физматлит, 2001.
4. Ильин В.А., Поздняк Э.К. Основы математического анализа. Т. 1-2. М.: Физматлит, 2004.
5. Кудрявцев Л.Д. Курс математического анализа. Т. 1-2. М.: Дрофа, 2003.
6. Берман Г.Н. Сборник задач по курсу математического анализа. СПб.: Профессия, 2005.
7. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: АСТ, 2004.
5.1.2. Дополнительная литература
1. Бутузов В.Ф. и др. Математический анализ в вопросах и задачах. М.: ФИЗМАТЛИТ, 2002,
480 с.
2. Зорич В.А. Математический анализ. Часть I. М.: МНЦМО, 2002, 664 с.
3. Зорич В.А. Математический анализ. Часть II. М.: МНЦМО, 2002, 794 с.
4. Краснов М.Л. и др. Векторный анализ. Задачи и примеры с подробными решениями. М.:
Едиториал УРСС, 2002, 144 с.
5. Краснов М.Л. и др. Функции комплексного переменного. Операционное исчисление.
Теория устойчивости. М.: Наука, 1981.
5.1.3. Методические разработки
1. Табуева В.А. Математика. Математический анализ. Специальные разделы. Учебное
пособие. 2-е изд. Екатеринбург. УГТУ-УПИ, 2004. 495 с.
2. Математика. Математический анализ. Специальные разделы. Контрольно-обучающие
работы. Индивидуальные задания. Расчетно-графические работы/ Под ред Табуевой В.А.
Екатеринбург. УГТУ-УПИ, 2004. 300 с.
3. Математика. Математический анализ. Специальные разделы. Индивидуальные домашние
задания. / Под редакцией В.А. Табуевой. Екатеринбург: ОАО "Полиграфист", 2001.
4. Махнев А.А., Мельникова Н.В., Мельников Ю.Б. Определенные и несобственные
интегралы. Интегралы, зависящие от параметра. Ряды. Учебное пособие для вузов по курсу
«Математика». Екатеринбург: Издательство Уральского университета, 2001. 226 с.
5.2. Электронные образовательные ресурсы
Раздел в стадии разработки.
5.3.
1.
2.
3.
4.
5.
Программное обеспечение
Программный пакет Mathcad 13 (v. 2000 Professional и выше);
Программный пакет Mathematica 5 (v. 4 и выше);
Программный пакет Maple 10 (v. 8 и выше);
Программный макрокоманд LaTeX и редактор технических текстов работающий с LaTeX –
WinEdt 4 (v. 3 и выше)
Программа NetSupport School (v.2.0 и выше).
5.4. Базы данных, информационно-справочные и поисковые системы
- http://www.intuit.ru/
-
http://www.edu.ru/
5.5. Фонд оценочных средств ()
Раздел в стадии разработки.
-
Информационные сервисы, обеспечивающие учебный процесс
http://study.ustu.ru
-
http://rtf.ustu.ru
-
http://vmumf.rtf.ustu.ru
5.6.
6. ПЕРЕЧЕНЬ КЛЮЧЕВЫХ СЛОВ ДИСЦИПЛИНЫ
№
раздел
а
Р1.Т1
Р1.Т2
Р1.Т3
Наименование раздела, темы
Введение в анализ
Ключевые слова
Множества, отображения
Числовые множества
Числовые функции
2
Р2.Т1
Р2.Т2
Р3.Т1
Теория предела
Непрерывность
Р4.Т1
Р4.Т2
Р4.Т3
Р4.Т4
Р4.Т5
Дифференциальное исчисление функций одной
действительной преременной
Р4.Т6
Р5.Т1
Вектор-функции
Р6.Т1
Р6.Т2
Р6.Т3
Неопределенный интеграл
Р6.Т4
Р7.Т1
Р7.Т2
Определенный интеграл
Р7.Т3
Р8.Т1
Р8.Т2
Предел и непрерывность ФНП
Р9.Т1
Р9.Т2
Р9.Т3
Р9.Т4
Р9.Т5
Р9.Т6
Дифференциальное исчисление ФНП
Р10.Т1
Р10.Т2
Р10.Т3
Р10.Т4
Р11.Т1
Р11.Т2
Интегралы по фигуре
Теория поля
Р11.Т3
Р11.Т4
Р12.Т1
Несобственные интегралы
Р12.Т2
Р13.Т1
Числовые ряды
Определение предела
Техника вычисления пределов
Непрерывность функции
Дифференцируемость, производная,
дифференциал
Техника дифференцирования
Основные теоремы дифференциального
исчисления
Правило Лопиталя
Формула Тейлора
Исследование функций
построение графиков
Построение кривых, заданных
параметрически
Основные методы интегрирования
Интегрирование дробно-рациональных
функций
Интегрирование иррациональных функций
Интегрирование тригонометрических и
гиперболических функций
Определение интеграла Римана
Методы вычисления определенных
интегралов
Приложения определенного интеграла
n
Пространство R
Предел и непрерывность ФНП
Определение дифференцируемости и
геометрические приложения
дифференциального исчисления ФНП
Частные производные и дифференциалы
высших порядков, формула Тейлора
Дифференцируемость отображений
Неявно заданные функции и отображения
Локальный экстремум ФНП
Условный экстремум
Общее определение интеграла по фигуре,
криволинейные интегралы 1-го рода
Двойные интегралы
Тройные интегралы
Поверхностные интегралы 1-го рода
Основные понятия теории поля. Поток,
линейный интеграл векторного поля
Интегральные формулы теории поля
Потенциальные и соленоидальные поля и
их свойства
Оператор Гамильтона
Определение, свойства, методы
интегрирования и исследование на
сходимость несобственных интегралов
Исследование несобственных интегралов
на абсолютную и условную сходимость
Определение и свойства сходящихся рядов,
исследование рядов на сходимость,
абсолютную/условную сходимость.
3
Р14.Т1
Р14.Т2
Функциональные ряды
Р14.Т3
Р15.Т1
Р15.Т2
Р15.Т3
Интегралы, зависящие от параметра
Р16.Т1
Р16.Т2
Р16.Т3
Р16.Т4
Р16.Т5
Р17.Т1
Функции комплексной переменной
Преобразование Лапласа
Р17.Т2
Р18.Т1
Р18.Т2
Ряды Фурье
Р19.Т1
Р19.Т2
Интеграл Фурье и преобразование Фурье
Область сходимости (абсолютной
сходимости) функционального ряда
Равномерная сходимость функциональных
рядов
Степенные ряды
Собственные интегралы, зависящие от
параметра
Несобственные интегралы, зависящие от
параметра
Интегралы Эйлера
Предел, непрерывность,
дифференцируемость ФКП
Интегрирование ФКП
Представление ФКП рядами
Особые точки ФКП и вычеты
Приложения теории вычетов
Преобразование Лапласа и его свойства
Применение преобразования Лапласа к
решению дифференциальных уравнений и
систем
Ряды Фурье в Евклидовых пространствах
Тригонометрические ряды Фурье
Представление непериодической функции
интегралом Фурье
Преобразование Фурье
4