Математика 2 курс 190629.01, 190629.07, 190631.01

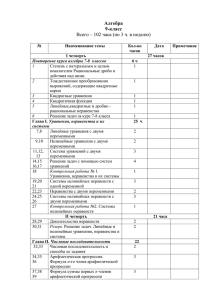
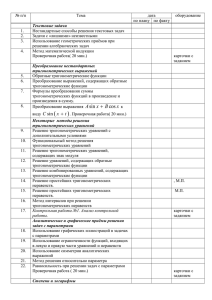
АННОТАЦИЯ РАБОЧЕЙ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
Математика
Специальность/профессия СПО
- 190631.01 «Автомеханик», 190629.01
«Машинист дорожных и строительных машин», 190629.07 «Машинист крана
(крановщик)»
Нормативный срок освоения ОПОП – 4 семестра
Уровень подготовки - базовый
Наименование квалификации - 18511 «Слесарь по ремонту автомобиля», 15594
«Оператор заправочных станций», 11442 «Водитель автомобиля категории В, С»,
13788 «Машинист крана авт.», 11424 «Водитель автомобиля категории С», 13583
«Машинист бульдозера», 19203 «Тракторист категории В, С, Е»
Цель и задачи учебной дисциплины – требования к результатам освоения:
В результате освоения дисциплины обучающийся должен уметь:
 выполнять арифметические действия над числами, сочетая устные и письменные
приемы; находить приближенные значения величин и погрешности вычислений
(абсолютная и относительная); сравнивать числовые выражения;
 находить значения корня, степени, логарифма, тригонометрических выражений на
основе определения, используя при необходимости инструментальные средства;
пользоваться приближенной оценкой при практических расчетах;
 выполнять преобразования выражений, применяя формулы, связанные со
свойствами степеней, логарифмов, тригонометрических функций;
 описывать взаимное расположение прямых и плоскостей в пространстве,
аргументировать свои суждения об этом расположении;
 применять координатный метод при решении пространственных задач;
 выполнять преобразования выражений, применяя формулы, связанные со
свойствами тригонометрических функций;
 вычислять значение функции по заданному значению аргумента при различных
способах задания функции;
 определять основные свойства числовых функций, иллюстрировать их на графиках;
строить графики изученных функций, иллюстрировать по графику свойства
элементарных функций; использовать понятие функции для описания и анализа
зависимостей величин;
 изображать основные многогранники и круглые тела; выполнять чертежи по
условиям задач; строить простейшие сечения куба, призмы, пирамиды;
 решать планиметрические и простейшие стереометрические задачи на нахождение
геометрических величин (длин, углов, площадей, объемов);
 использовать при решении стереометрических задач планиметрические факты и
методы;
 находить производные элементарных функций; использовать производную для
изучения свойств функций и построения графиков; применять производную для
проведения приближенных вычислений, решать задачи прикладного характера на
нахождение наибольшего и наименьшего значения; вычислять в простейших случаях
площади и объемы с использованием определенного интеграла; использовать
приобретенные знания и умения в практической деятельности и повседневной жизни
для: решения прикладных задач, в том числе социально-экономических и физических,
на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
 решать рациональные, показательные, логарифмические, тригонометрические
уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и
системы; использовать графический метод решения уравнений и неравенств;
изображать на координатной плоскости решения уравнений, неравенств и систем с
двумя неизвестными; составлять и решать уравнения и неравенства, связывающие
неизвестные величины в текстовых (в том числе прикладных) задачах;
 решать простейшие комбинаторные задачи методом перебора, а также с
использованием известных формул;
 вычислять в простейших случаях вероятности событий на основе подсчета числа
исходов.
В результате освоения дисциплины обучающийся должен знать:
 классификацию чисел, основные правила и формулы преобразования
алгебраических выражений;
 основные правила и формулы стереометрии и их применение при решении
пространственных задач;
 основы тригонометрии;
 свойства основных элементарных функций и определение их по графику;
 начала математического анализа;
 основные способы и методы решения уравнений, неравенств и систем уравнений и
неравенств;
 основы теории вероятности и математической статистики.
Наименование разделов и тем дисциплины:
Раздел 1. Развитие понятия о числе
Раздел 2. Функции, их свойства и графики
Раздел 3. Корни, степени и логарифмы
Раздел 4. Основы тригонометрии
Раздел 5. Прямые и плоскости в пространстве
Раздел 6. Координаты и векторы
Раздел 7. Многогранники
Раздел 8. Тела и поверхности вращения
Раздел 9. Измерения в геометрии
Раздел 10. Начала математического анализа
Раздел 11. Комбинаторика, статистика, теория вероятностей
Раздел 12. Уравнения и неравенства
Раздел 13. Обобщающее повторение курса
Программой учебной дисциплины предусмотрены следующие виды учебной
работы:
Вид учебной работы
Максимальная учебная нагрузка (всего)
Обязательная аудиторная нагрузка
в том числе: лекции
практические занятия
Самостоятельная работа студента (всего)
Форма итоговой аттестации – экзамен
Всего
часов
431
291
91
200
140
Программа дисциплины относится к общеобразовательному циклу.
Программа дисциплины включает в себя цель и задачи дисциплины, место
дисциплины в структуре ОПОП, требования к результатам освоения дисциплины,
объем дисциплины и виды учебной работы, содержание дисциплины, учебнометодическое и информационное обеспечение дисциплины (основная,
дополнительная литература, собственное учебно-методическое обеспечение),
методические рекомендации по организации изучения дисциплины.