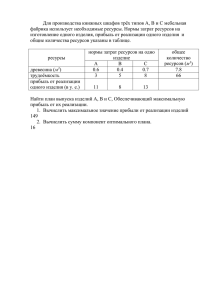
Вопрос 1 Вычислить J= ∫cos(lnx) dx/x sin(lnx)+ C Вопрос 2 При каком положительном значении параметра t прямые, заданные уравнениями 3tx 8y + 1 = 0 и (1+t)x 2ty = 0, параллельны? 2 Вопрос 3 Составьте уравнение плоскости, зная, что точка А(1, 1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости. x - y + 3z - 11 = 0 Вопрос 4 Найти наименьшее значение функции y = x 2 – 6x + 5 на отрезке (1,2). -3 Вопрос 5 Найти lim x-->0 (5x - cos x) 0 Вопрос 6 Решить систему уравнений: 2x1 + 3x2 + 2x3 = 9 x1 + 2x2 – 3x3 =14 3x1 + 4x2 + x3 = 16 х1 2 х2 3 х3 -2 Вопрос 7 Вычислить определитель D, разложив его по элементам второго столбца. D= -20 Вопрос 8 Найти производную функции y =ln sinx ctg x Вопрос 9 Вычислить площадь фигуры, ограниченной линиями 4y = x2 , y2 = 4x. 16/3 Вопрос 10 Найдите угол между векторами a = 2m+4n и b = m-n, где m и n - единичные векторы и угол между m и n равен 120о 120