Теория и методика обучения математике в понятиях, схемах и таблицах, Шмигирилова И.Б., 2007

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН Северо-Казахстанский государственный университет им. М. Козыбаева И.Б. ШМИГИРИЛОВА ТЕОРИЯ И МЕТОДИКА ОБУЧЕНИЯ МАТЕМАТИКЕ В ПОНЯТИЯХ, СХЕМАХ И ТАБЛИЦАХ Учебно-методическое пособие Петропавловск 2007 ББК 74.262.21 УДК 372.016:51(075.8) Ш 73 Издается по решению «Учебно-методического Совета СевероКазахстанского государственного университета им. М. Козыбаева» (протокол № от ) Рецензенты: зав. кафедрой ТМНДО СКГУ, к.п.н. Кучер Т. П., ст. преподаватель Сев. Каз. обл. ИПК и ППК Касенова А.Е. Шмигирилова И.Б. Ш 73 Теория и методика обучения математике в понятиях, схемах и таблицах: учебно-методическое пособие. Петропавловск, 2007 г.- 161 с. В настоящем пособии в краткой и наглядной форме рассмотрены основные вопросы теории и методики обучения математике. Содержание и структура пособия соответствует требованиям стандарта образования. Предлагаемое пособие предназначено для студентов педагогических специальностей вузов для подготовки к практическим и лабораторным занятия. Пособие может быть использовано в рамках СРС и СРСП студентами дневной, заочной и дистанционной форм обучения. Кроме того, пособие будет безусловно полезно при подготовке к экзамену. УДК 372.016:51(075.8) ББК 74.262.21 Ш 73  Шмигирилова И.Б. 2 ПРЕДИСЛОВИЕ  СКГУ, 2007 В пособии нашли свое отражение современное изложение основных вопросов теории и методики обучения математике. Предлагаемое пособие содержит не только материал по общей методике математики, но и освещает основные вопросы по частной методике. Методика преподавания конкретных разделов курса математики средней школы раскрывается по содержательно-методическим линиям, что позволяет выстроить единый подход к изложению материала. Пособие написано с учетом программы по дисциплине «Теория и методика обучения математики» и программы по математике для средней школы, адресовано студентам математических специальностей и специальностей с соответствующей специализацией. При разработке содержания пособия автор исходила из следующих положений: 1. В пособии должны быть изложены основные вопросы, без знания которых не возможна методическая подготовка учителя математики. 2. Изложение по структуре должно отличаться от соответствующего лекционного курса, так как, с одной стороны, менее детализировано, с другой стороны, более информативно. 3. Многие вопросы рассматриваются в пособии в расчете на то, чтобы представить основную структуру изучаемого раздела. Поэтому пособие должно содержать достаточный список литературы, которая может быть полезна студентам при самостоятельной работе для изучения отдельных вопросов более углубленно и творчески. В пособии выражены основные принципы подходов к изучению дисциплины, содержится информация, изложенная автором в обобщенном и систематизированном виде. Пособие включает сведения, являющиеся результатом осмысления и анализа большого количества литературы по психологии, педагогике, общей и частной методике обучения математике, 3 которые были систематизированы и обобщены на основе накопленного опыта преподавания данной дисциплины в вузе и курса математики в средней школе. Включенные в пособие схемы и таблицы позволяют достичь как ситуативного, так и долгосрочного эффекта в запоминании и осмыслении учебного материала. 4 РАЗДЕЛ 1. ОБЩАЯ МЕТОДИКА ПРЕДМЕТ ТЕОРИИ И МЕТОДИКИ ОБУЧЕНИ МАТЕМАТИКЕ Теория и методика преподавания математики (ТМОМ) - раздел педагогики, исследующий закономерности обучения математике на определенном уровне ее развития в соответствии с целями обучения подрастающего поколения, поставленными обществом; - теория и методика обучения математике - это педагогическая наука о задачах, содержании и методах обучения математике; - теория и методика преподавания математики - наука о математике как учебном предмете и закономерностях процесса обучения математике учащихся различных возрастных групп и способностей. Основные вопросы решаемые ТМОМ Зачем учить математике? Что изучать из математики? Как обучать математике? Определение целей обучения математике Отбор содержания учебного предмета математики в соответствии с целями Разработка наиболее рациональных методов обучения и рекомендаций по их применению в практике работы учителя 5 Структура теории и методики обучения математике Общая методика включает в себя вопросы дидактики, приспособленные к процессу обучения математике. Примеры: структура урока математики; методика обучения решению задач и др. Частная методика включает в себя вопросы общей методики, адаптированные к изучению основных методических линий и разделов школьного курса математики. Примеры: методика обучения тождественным преобразованиям; методика изучения функций и др Конкретная методика включает в себя вопросы освящающие процесс обучения в рамках отдельных тем школьного курса математики, отдельных вопросов, теорем и т.д. Примеры: методика доказательства признаков равенства треугольников; методика обучения решению задач на составление уравнений и др. ЦЕЛИ, ЗАДАЧИ И ФУНКЦИИ ОБУЧЕНИЯ 6 Уровни целеполагания Системный Формулировка общих целей школьного образования Предметный Выбор общей ориентации (профиль и уровень обучения) Модульный Выбор дидактической системы (вклад в реализацию общих целей) Поурочный Создание методического обеспечения Общие цели обучения математике 1) Передача конкретных математических знаний, необходимыми в практической деятельности, для изучения смежных дисциплин, для продолжение образования; 2) интеллектуальное развитие учащихся, формирование умений, навыков и качеств мышления, характерных для математической деятельности и необходимых человеку для полноценного функционирования в обществе; 3) формирование представления об идеях и методах математики, о математике как форме описания и методе познания действительности; 4) формирование представления о математике как части общечеловеческой культуры. 7 Функции обучения математике образовательная Обуславливает овладение знаниями и формирование мировоззрения воспитательная Формирование интереса и устойчивой мотивации к учебной деятельности развивающая Формирование познавательных психических процессов и свойств личности, логических приемов мыслительной деятельности. Составляющей развивающей функции является эвристическая: обучение эвристическим приемам информационная Получение необходимого объема информации о прошлом, настоящем и будущем математики и ее приложениях прогностическая Формирование прогностических умений: выявлять нерешенные проблемы, выдвигать гипотезы, видеть иное решение проблемы эстетическая Воспитание эстетического вкуса на материале математики прикладная Формирование умения математически исследовать явления реального мира контрольнооценочная Осуществление контроля, оценки знаний и умений интегрирующая Формировании системности знаний 8 Задачи обучения математике образовательные: овладение учащимися системой математических знаний, умений и навыков, дающей представление о предмете математики, о математических приемах и методах познания, применяемых в математике; воспитательные: воспитание активности, самостоятельности, ответственности; нравственности, культуры общения; эстетической культуры, графической культуры школьников; развивающие: формирование мировоззрения учащихся, развитие всех составляющих мышления, развитие пространственного воображения. СОСТАВНЫЕ ЧАСТИ СОДЕРЖАНИЯ ОБУЧЕНИЯ И ИХ ХАРАКТЕРИСТИКИ Составные части процесса обучения Результат познавательной ЗНАНИЯ деятельности, отраженный в сознании человека в виде представлений, фактов понятий законов теорий. Владение способами, приемами УМЕНИЯ применения усваиваемых знаний на практике. Умения, доведенные до высокой НАВЫКИ степени совершенства. Владение способами и приемами МЫШЛЕНИЕ умственной деятельности. 9 Параметры знаний 1 Полнота Способность выделить все элементы учебного материала и их связи друг с другом 2 Оперативность Способность применить имеющиеся знания в вариативных ситуациях 3 Глубина Способность выделить элементы учебного материала в их взаимосвязи 4 Гибкость Способность самостоятельно применить или сконструировать несколько способов решения к одной и той же задаче или разработать нестандартный подход к решению проблемы 5 Конкретность и обобщенность 6 Свернутость и развернутость 7 Систематичность 8 Осознанность Способность выделить обобщенное знание, подводить конкретные задания под обобщенные, относить частное к общему Способность излагать свои знания компактно, умение развернуть свои знания при необходимости подробного изложения Умение определить иерархию понятий в их последовательности и взаимосвязи Умение перегруппировывать и преобразовывать материал, творчески применять его 10 Характеристики уровней усвоения информации Уровень Название уровня Характеристика усвоения уровня Отсутствие у обучающеегося опыта (знаний) в конкретном виде 0 деятель-ности, но вместе «понимание» с тем имеется готовность (нулевой) к восприятию новой инфор-мации, т.е. наличие обуча-емости. Умение выполнить каждую операцию деятельности, с опорой на описание алгоритма, I «узнавание» подсказку, намек (репродуктивное действие). Умение самостоятельно воспроизвести и применить информацию в ранее рассмотренных II «воспроизведение» типовых ситуациях, при этом деятельность является репродуктивной. Способность использовать приобретенные знания и умения в нетиповых III «применение» ситуациях, т.е. деятельность является продуктивной. Умение действовать в непредвиденных ситуациях, создание IV «творчество» новых правил, алгоритмов действий, 11 продуцировать информацию. новую Сущность навыка Компонент 1 Собственно обученность человека, как чистая составляющая навыка, обычно включающая систему реакций, координации движений, их согласования в процессе деятельности. Компонент 2 Выработанная в процессе упражнений способность человека адаптироваться к конкретным условиям деятельности и реализовывать полученные знания. основные компоненты НАВЫК этапы формирования Автоматизация – придание действию плавности и нужной скорости, снятие напряжения Синтетический – этап, представляющий объединение изученных элементов в целостное действие Аналитический – этап, представляющий вычленение и овладение отдельными элементами 12 действия ПРИНЦИПЫ ОБУЧЕНИЯ Принципы обучения – руководящие идеи, нормативные требования к организации и осуществлению образовательного процесса. СИСТЕМА ОСНОВНЫХ ПРИНЦИПОВ ОБУЧЕНИЯ Принцип научности: содержание обучения должно объективно отражать современное состояние соответствующей отрасли научного знания. Принцип сознательности и активности: осознание обучаемыми целей и задач обучения, стимулирование познавательной активности обучаемых с помощью эффективных методов. Принцип систематичности, последовательности и комплексности: обуславливается соблюдением логики изучаемой науки, системным характером учебной деятельности, четким планированием учебных занятий. Принцип наглядности: обучение должно строится на рациональном использовании наглядности Принцип прочности: установка на прочное и длительное воспоминание, систематическая организация повторения ранее изученного материала 13 Принцип доступности: учет уровня подготовленности возрастных и индивидуальных особенностей обучающихся, соотнесенный с 14 Принципы личностно-ориентированного обучения Принцип личностного целеполагания: учет личных учебных целей учащихся. Принцип выбора индивидуальной образовательной траектории: ученик имеет право на осознанный и согласованный с педагогом выбор основных компонентов своего образования. 3 Принцип продуктивности обучения: главный ориентир обучения – личное образовательное приращение ученика. 4 Принцип первичности образовательной продукции: создаваемое учеником личностное содержание образования опережает изучение образовательных стандартов и общепризнанных достижений в изучаемой области. 1 2 5 Принцип ситуативности обучения: 6 Принцип образовательной рефлексии: образовательный процесс строится на ситуациях, предполагающих самоопределение учеников и поиск их решения. Учитель сопровождает ученика в его образовательном движении. образовательный процесс сопровождается его рефлексивным осознанием субъектами образования. 15 МЕТОДЫ ОБУЧЕНИЯ МАТЕМАТИКЕ Автор Формулировка понятия «метод обучения» 1 2 Бабанский Ю.К. Метод обучения – упорядоченный Блох А.Я. способ взаимосвязанной деятельности Зверев И.Д. учителя и учащихся, направленный на Столяр А.А. достижение целей обучения. Хуторской А.В. Лернер И.Я. Метод обучения – способы организации Скаткин М.Н. и УПД учащихся, обеспечивающие др. овладение знаниями, методами познания и практической деятельности. Метод обучения – многоаспектное Бабанский Ю.К. явление, характеризующиеся набором признаков: - быть определенной формой движения содержания; - выступать как способ раскрытия содержания знания; - выступать определенным способом обмена информацией между учителем и учащимися и между учащимися; быть определенным способом управления учебно-познавательной деятельности (УПД); - быть способом общения учителя и учащихся, а также учащихся между собой; выступать в роли способа контроля. Левина М.М. Метод обучения – система Шамова Т.И. целенаправленных действий педагога, организующих познавательную и практическую деятельность обучаемых и обеспечивающих решение задач обучения. 16 1 2 Калягин Ю.М. и Метод обучения – упорядоченный др. комплекс дидактических приемов и средств, посредством которых реализуются цели обучения, воспитания и развития учащихся на том или ином этапе обучения, трансформируясь из целей преподавания в цели учения. Давыдов В.В. Метод обучения – система последовательных взаимосвязанных действий учителя и учащихся обеспечивающих усвоение содержание образования. Махмутов М.И. Метод обучения – модель поведения – регулятив, содержащий совокупность правил, предписывающих, определяющих целевую направленность деятельности в обучении и реализуемых через конкретные действия – приемы и способы деятельности. ДьяченкоВ.К. Метод обучения – организационная структура учебного процесса в действии. Машбиц Е.И. Метод обучения – способ определенной Костюк Г.С. организации работы учащихся с учебным материалом. Схема описания метода обучения: Описание деятельности учителя способ связи меду ними Описание учебнопознавательной деятельности учащихся Схема выбора методов обучения: 17 Общие цели образования Особенности изучаемого курса Цели конкретного урока Возможности учащихся Формы обучения Имеющиеся средствами обучения; Способности и предпочтениями учителя Особенности используемой учителем дидактической системы. Наличие времени МЕТОДЫ ОБУЧЕНИЯ Классификация методов обучения 18 Основания для классификации 1 Источник знаний Этапы обучения Способ руководства УПД учащихся Логика педагогического обучения Характер познавательной деятельности (Лернер И.Я., Скаткин М.Н.) Методы 2 Словесные (Объяснение, рассказ, беседа, устное инструктирование, лекция и др.) Наглядные (Наблюдение, демонстрация, работа с книгой, таблицей, чертежом и др.) Практические (Практические и лабораторные работы, самостоятельные демонстрации, создание моделей и др.) Методы подготовки к изучению нового материала Методы изучение нового материала Методы закрепления и упражнений Методы контроля и оценки Работа под руководством учителя Самостоятельная работа Индуктивные Дедуктивные Аналитические Синтетические Объяснительно-иллюстративные Репродуктивные Проблемного изложения Частично-поисковые Исследовательские 1 2 19 Организации учебной деятельности Стимулирования Релаксации Контроля и оценки (Бабанский Ю.К.) Дидактические задачи Коммуникативные Познавательные Преобразовательные Систематизирующие Контрольные (Онищук В.А.) Когнитивные Креативные Оргдеятельностные (Хуторской А.В.) Форма движения индуктивно-репродуктивный; деятельностей дедуктивно-репродуктивный; учителя, ученика обобщенно репродуктивный; и индуктивно-эвристический; математического дедуктивно-эвристический; содержание эвристическое обобщение; (Саранцев Г.И.) индуктивно-исслеловательский; «преподавание – дедуктивно-исслеловательский; обобщенное исследование. предметное содержание – учение» Схема рационального применения различных методов обучения 20 Словесные Наглядные Репродуктивные Поисковые 1 2 При формировании теоретических и фактических знаний 3 4 Какие возможности должен иметь учитель для использования данного метода При каких особенностях учащихся рационально применять этот метод При каком содержании учебного материала особенно рационально применять этот метод При решении каких задач этот метод применяется особенно успешно применение Методы 1 5 Когда материал носит преимущественно теоретикоинформационный характер Для развития Когда содернаблюдажание учебтельности, ного материповышения ала может внимания к быть предизучаемым ставлено вопросам средствами наглядности Для Когда формирова- содержание ния знаний и слишком навыков сложно или весьма просто Когда ученики готовы к усвоению словесной формы Для развития самостоятельности мышления, исследовательских умений, творческого подхода к делу Когда содержание материала имеет средний уровень сложности. Когда ученики подготовлены к проблемному изучению данной темы Когда учитель имеет время для проблемного изучения темы и хорошо владеет поисковыми методами обучения 2 3 4 5 21 Когда учитель владеет этим методом лучше, чем другими Когда наглядные пособия доступны ученикам данного класса Когда учитель располагает необходимыми наглядными пособиями или может изготовить их самостоятельно Когда учеКогда учитель ники еще не не имеет готовы к времени для проблемному проблемного изучению изучения этой темы данной темы Практические Методы самостоятельной работы Индуктивные Дедуктивные Для развития практических умений и навыков Когда содержание темы включает практческие упражнения, проведение опытов, выполнение трудовых заданий Когда Когда учитель ученики располагает готовы к учебновыполнению материальныпрактических ми пособиями, дидактическим заданий и материалами для организации практических упражнений Для развития Когда самостоматериал ятельности в доступен для самосучебной деятельности, тоятельного формирова- изучения ния навыков учебного труда Когда ученики готовы к самостоятельному изучению данной темы Когда имеются дидактические материалы для самостоятельной работы учеников и время, чтобы ее организовать на уроке Для развития умений обобщать, осуществлять индуктивные умозаключения Когда содержание темы изложено в учебнике индуктивно или его рациональнее изложить таким образом Когда ученики готовы к индуктивным рассуждениям и затрудняяются в дедуктивных рассуждениях Когда учитель владеет индуктивными методами обучения (обычно учителя владеют ими) Для развития умения осуществять дедуктивные умозаключения и развития умения анализировать Когда содержание темы изложено в учебнике дедуктивно или его особенно рационально изложить подобным образом Когда ученики подготовлены к дедуктивным рассуждениям Когда учитель владеет дедуктив-ными методами обучения ФОРМЫ ОБУЧЕНИЯ 22 Формы организации УПД – способ, характер взаимодействия педагога и учащихся, учащихся между собой. 1) индивидуальная (взаимодействие учителя с одним учеником); 2) фронтальная (работа учителя со всем классом, где учащиеся не взаимодействуют друг с другом); 3) групповая (работа учащихся в группах по 4-6 человек); 1) коллективная (учащиеся класса выполняют задания как целостный коллектив). Форма учебных занятий – характер взаимодействия учащихся с изучаемым материалом: урок, лекция, семинар, практикум, домашняя работа, экзамен, консультация, экскурсия, кружок, факультатив и т.д СРЕДСТВА ОБУЧЕНИЯ Средства обучения – орудия деятельности учителя и учащихся, представляют собой материальные и идеальные объекты, которые вовлекаются в образовательный процесс в качестве носителей информации и инструмента деятельности. Зависимость запоминания информации от ее расположения на доске 28 % 33 % 16 % 23% 23 Дидактические функции средств обучения Дидактические функции средств обучения передача учебной информации учет психологических особенностей восприятия учебного материала учащимися уменьшение затрат времени визуализация информации обеспечение аналитической и синтетической деятельности педагога и учащегося Усвоение учебной информации при разовом выполнении определенного вида учебной деятельности 100 90 80 70 60 50 40 30 20 24 слух, зрение, обсуждение, обобщение слух, зрение, обсуждение слух и зрение зрение слух 0 10 чтение 20 Классификация средств обучения Основания для классификации По составу объектов По отношению к источникам появления По сложности По способу использования По особенностям строения По характеру использования По носителю информации По уровням содержания образования По отношению к технологическому прогрессу Средства обучения Материальные Идеальные Искусственные Естественные Простые Сложные Динамичные Статичные Плоские Объемные Смешанные Виртуальные Визуальные Аудиальные Аудио-визуальные Бумажные Электронные Лазерные и др. На уровне урока На уровне предмета На уровне процесса обучения Традиционные Современные Перспективные 25 Подготовка урока с использованием средств обучения Проанализировать цели урока, его содержание и логику изучения материала. Выделить главные элементы, которые должны быть усвоены учащимися. Установить, на каком этапе и для какой цели необходимо использовать средства обучения. Отобрать оптимальные средства обучения. Определить методы и приемы, с помощью которых будет обеспечена познавательная деятельность учащихся. Отражение использование выбранных средств и методики работы с ними в конспекте урока. 26 К КОНТРОЛЬ И ОЦЕНКА ЗНАНИЙ Контроль Формы контроля 27 Тестирование, анкетирование, контрольная работа, лабораторная работа, устный опрос, зачет, экзамен, проект, образовательные ситуации и др. Контроль знаний учащихся должен быть: • мотивированным; • систематическим и регулярным; • разнообразным по формам, включающим всех учащихся в работу; • всесторонним и объективным на основе дифференцированного подхода к учащимся; базироваться на единстве требований учителей, осуществляющих контроль за учебной работой учащихся. Педагогические требования к контролю й Выявление, измерение и оценивание знаний, умений, навыков, способов деятельности учащихся. Функции оценки Оценка Деятельность или действие по оцениванию; отметка – результат этой деятельности. Способы выражения оценки Устные суждения педагога, письменные качественные характеристики, цифровые отметки и т.д. • мотивационная – поощрение и стимулирование образовательной деятельности; • диагностическая – выявление причин тех или иных образовательных результатов; • воспитательная – формирование самосознания и адекватной самооценки школьника; • информационная – фиксация информации о степени успешности ученика в достижении образовательных стандартов. УРОК - ОСНОВНАЯ ФОРМА ОБУЧЕНИЯ 28 Урок - логически законченный, целостный, ограниченный определенными рамками времени отрезок учебновоспитательного процесса, где представлены все основные элементы этого процесса (цели, содержание, средства, методы, формы организации). Исходная идея современного урока: единство обучения, воспитания и развития. Общая функция урока: целостное формирование личности на основе воспитывающего и развивающего обучения. Триединая цель урока познавательный аспект воспитывающий аспект развивающий аспект Учебно-воспитательные задачи (УВЗ) урока 1 2 3 4 5 … Триединая цель урока (ТЦУ) – заранее запрограммированный учителем результат, который должен быть достигнут в конце урока. 29 Триединая цель урока познавательный аспект 1. Научить каждого ученика самостоятельно добывать знания. 2. Осуществлять главные требования к овладению знаниями. 3. Формировать умения и навыки, обеспечивающие успешное выполнение УПД и продвижение по индивидуальной образовательной траектории. развивающий аспект 1. Развитие речи: обогащение и усложнении ее словарного запаса, усложнение ее смысловой функции, усиление коммуникативных свойств речи 2. Развитие мышления: анализировать, выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия, ставить и разрешать проблемы. 3. Развитие сенсорной сферы. 4. Развитие двигательной сферы. 30 воспитывающий аспект 1. Влияние на становление качеств личности учащихся: нравственности, трудолюбия, эстетического вкуса, патриотизма, экологической культуры и других общечеловеческих ценностей. Конечный результат урока (КРУ) Результат работы учителя 1) целенаправленность его деятельности на уроке; 2) характер отношений с учащимися; 3) индивидуальноличностный подход к учащимся; 4) умение приводить в соответствие содержание, методы, средства и формы обучения; 5) работа по формированию и развитию общеучебных навыков и умений; 6) работа по развитию познавательного интереса; 7) работа по формированию ЗУНов и вооружение учащихся способами УПД; 8) развитие общих способностей учащихся; 9) объективность оценки знаний учащихся, соединение оценки и отметки; 10) эффективность усилий по развитию личности; 11) эффективность воспитывающих влияний. 31 Результаты работы учащихся 1) уровень самостоятельности на уроке; 2) отношение учащихся к учебному труду; 3) отношение к предмету, учителю, к друг другу; 4) объективная направленность деятельности на образование и развитие своей личности; 5) наличие познавательного интереса; 6) воспитательная и развивающая подвижка личности, возникшая в ходе урока; 7) знание фактического материала и уровень его усвоения. Состав комбинированного урока и содержание его этапов I. Организационный: обеспечить подготовку учащихся к работе на уроке. Эта пи его УВЗ 1 Содержание этапа Условия достижения положительных результатов 2 3 1. Приветствие. 1.Сосредоточен2. Определение ность, отсутствующих самообладание, . собранность 3. Проверка учителя. готовности 2. Отсутствие учащихся к многословия, уроку. ярко выраженная волевая 4. Проверка направленность. подготовленности 3. Использование небольшой классного помещения к психологическо й паузы для уроку. 5. Организация побуждения к внимания. вниманию. 4. Последовательность и постоянство в предъявлении требований. 32 Показатель выполнения психологическо й задачи этапа 4 1. Доброжелательный настрой учителя и учащихся. 2. Кратковременность организационного момента (1-2 мин). 3. Полная готовность учащихся, классного помещения и оборудования. 4. Быстрое включение класса в деловой ритм. 5. Организация внимания всех учащихся. II. Проверка домашнего задания: проверить правильность, полноту и осознанность выполнения домашней работы всеми учащимися, ликвидировать ошибок. 1 2 1. Выявление факта выполнения домашнего задания всеми учащимися класса. 2. Обязательное выяснение причин евыполнеия задания отдельными учащимися. 3. Определение типичных недостатков в знаниях и причин их появления. 4. Исправление ошибок допущенных в домашней работе. 5. Привлечение к проверке, по возможности, учениковконсультантов или дежурных. 6. Использование взаимопомощи и самоконтроля. 3 1. Оперативность и целевая направленность деятельности учителя. 2. Использование системы приемов, позволяющих проверить выполнение задания у всех учащихся класса. 3. Осознание учащимися взаимосвязи домашнего задания с результатами своего обучения. 33 4 1. Выявление факта выполнения домашнего задания, установление и ликвидация типичных ошибок в короткий промежуток времени (5-7 мин.). 2. Использование различных форм контроля в зависимости от содержания, вида и цели домашнего задания, а также от отношения учащихся к выполнению домашней работы. 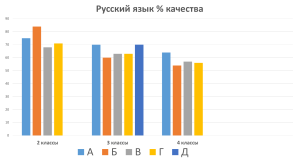III. Всесторонняя проверка знаний: глубоко и всесторонне проверить знания группы учащихся, выявление причин недостатков в ЗУНах и их коррекция. 1 2 1. Проверка различными методами объема и качества усвоения материала отдельными учащимися. 2. Проверка организации мыслительной деятельности учащихся. 3. Проверка сформированности общеучебных и социальных навыков и умений. 4. Комментирование (оценивание) ответов учащихся. 5. Организация деятельности класса во время ответа вызванных учащихся. 3 1. Использование различных методов проверки знаний. 2. Практика постановки дополнительных вопросов для проверки прочности, глубины и осознанности знаний. 3. Создание в процессе вопроса нестандартных ситуаций в использовании знаний. 4. Привлечение всех учащихся класса к активному слушанию и рецензированию ответов. 5. Создание атмосферы значимости и важности этапа. 34 4 1. Проверка выполнения всех требований к знаниям учащихся. 2. Рецензирование ответов, направленное на указание положительных и отрицательных сторон в ЗУНах учащихся. 3. Коррекция ЗУНов. 4. Активная деятельность всего класса в ходе проверки знаний отдельных учащихся. IV. Подготовка к активному и сознательному усвоению материала: организовать деятельность учащихся, подготовить их к усвоению нового материала 1 2 1. Сообщение новой темы. 2. Формулирование совместно с учащимися цели и задач изучения нового материала. 3. Показ практической значимости нового материала, мотивация учащихся к его усвоению. 4. Постановка перед учащимися учебной проблемы. 3 1. Предварительное продумывание учителем цели, задач, практической значимости нового материала и учебной проблемы. 2. Умение четко представить учащимся чему они должны научиться на уроке. 3. Осознание учащимися целей и задач изучения нового материала. 35 4 1. Активная познавательная деятельность учащихся на последующих этапах. 2. Эффективность восприятия осмысления нового материала. 3. Осознание важности и значимости нового материала. V. Усвоение новых знаний: дать учащимся конкретное представление об изучаемом материале, выработать соответствующие знания и навыки. 1 2 1. Организация внимания. 2. Организация процесса восприятия, осознания, осмысление, первичного обобщения и систематизации нового материала. 3. Формировать у учащихся приемы УПД по изучению материала. 3 1. Актуализации опыта и опорных знаний учащихся. 2. Использование приемов активизации мыслительной УПД учащихся, включение их в поисковую работу и самоорганизацию в процессе учения. 3. Максимальное творческое участие школьников в освоении нового материала. 36 4 1. Качество ответов учащихся на следующем уроке. 2. Качество выполнения работы по самостоятельному применению нового материала. 2 1. Закрепление новых ЗУНов. 2. Закрепление методики изучения вопр оса. 3. Углубление усвоения материала, проверка понимания учащимися сущности новых понятий. 4. Творческое применение материала на практике и в нестандартных ситуациях. VI. Закрепление новых знаний: закрепить в памяти учащихся ЗУНы, которые необходимы им для самостоятельной работы по новому материалу, повышения уровня осмысленности материала 1 3 1. Оперирование знаниями, решение на их основе практических и творческих задач. 2. Использование различных способов закрепления знаний, вопросов требующих мыслительной активности и самомтоятельности. 3. Обращение к классу с требованием дополнить, уточнить, исправить и т.д. 4. Определение по количеству и качеству дополнительных ответов качества понимания нового материала. 37 4 1. Прочность и уровень осознанности знаний учащихся. 2. Умение учащихся соотносить отдельные части материала друг с другом. 3. Умение воспроизводить основные идеи и существенные факты нового материала. VII. Информация о домашнем задании и инструктаж по его выполнению: сообщение о содержании и методике выполнения домашнего задания 1 2 1. Мотивирование домашнего задания: стремление к усовершенствованию знаний, интересная постановка проблемы, апеллирование к чувству долга. 2. Краткий, но четкий инструктаж по выполнению домашнего задания. 3. Проверка того, как учащиеся поняли содержание домашней работы и способы ее выполнения. 3 1. Обязательное выполнение этапа в границах урока, до звонка. 2. Необходимо отводить достаточное время, чтобы задача была выполнена. 3. Задание должно проходить при полном внимании всего класса. 4. Добиваться, чтобы содержание домашнего задания было понято всеми учащимися без исключения. 38 4 1. Правильное выполнение домашнего задания всеми учащимися класса (выясняется на следующем уроке). VIII. Итог урока 1. Подвести итог урока: как работал класс, кто работал особенно старательно, что нового узнали учащиеся. 1. Привлекать учащихся к подведению итога урока. 1. Превращение ЗУНов в личный образовательный продукт. Типология уроков Типы урока Структура урока Комбинированный В структуру урока входят все этапы. урок Все этапы равнозначны. Урок усвоения В структуру урока входят 1, 4, 5, 6, 7, 8 нового материала этапы. Основной этап – 5. Этап усвоения новых знаний. Урок закрепление В структуру урока входят 1, 4, 6, 7, 8 материала этапы. Основной этап – 6. Этап закрепления знаний. Урок повторения В структуру урока входят 1, 7, 8 этапы и этап повторения, который включает в себя 3 и 6 этапы, переконструированные под задачи данного типа урока. Именно этап повторения является основным Урок обобщения и В структуру урока входят 1, 7, 8 этапы систематизации и этап обобщения и систематизации изученного изученного, который включает в себя 3 и 6 этапы, переконструированные под задачи данного типа урока. Именно этап обобщения и систематизации изученного является основным Урок проверки и В структуру урока входят 1, 2, 3, оценки знаний 7, 8 этапы. Основной этап – 3. Этап проверки и оценки знаний. 39 Типы уроков Урок изучения нового материала. Урок совершенствования знаний умений и навыков (уроки формирования умений и навыков, целевого применение усвоенного и т.д.) Урок контроля (учета и оценки знаний, умений и навыков учащихся) Виды уроков а) урок-лекция. б) урок-беседа. в) урок с использованием учебного кинофильма. г) урок теоретических или практических самостоятельных работ (т.е. исследовательского типа); д) урок смешанный (т.е. сочетание различных видов на одном уроке). а) урок самостоятельных работ (репродуктивного типа); б) урок лабораторная работа; в) урок - практических работ; г) урок – семинар; д) урок-практикум (урок поиска рациональных решений, урок одной задачи). а) устная форма проверки (фронтальный, индивидуальный, групповой опрос); б) зачет; в) практические и лабораторные работы; г) контрольные (самостоятельные) работы и др. 40 Нетрадиционные уроки а) Ролевые или деловые игры; б) ''Круглый стол'' или конференция; в) урок открытых мыслей; г) аукцион знаний; д) урок – конкурс, урок – диспут; е) межпредметный интегрированный урок; ж) театрализованный урок; з) урок-экскурсия 41 Требования к современному уроку Психологические требования Дидактические требования Методические требования Требования к подготовке и организации урока Требования к структуре урока Требования к содержанию и процессу учения Требования к технике проведения урока Реализация совокупности требований к системе уроков обеспечит необходимый уровень качества организации уроков, а следовательно и их эффективности. 42 Дидактические требования 1. Четкое формулирование образовательных задач в целом и его составных элементов, их связь с развивающими и воспитательными задачами. 2. Определение оптимального содержания урока в соответствии с требованиями учебной программы и целями урока, с учетом уровня подготовки и подготовленности учащихся. 3. Прогнозирование уровня усвоения учащимися научных знаний, сформированных умений и навыков как на уроке, так и на отдельных его этапах. 4. Выбор наиболее рациональных методов, приемов и средств обучения, стимулирования и контроля. Их оптимального воздействия на каждом этапе урока. Выбор, обеспечивающий познавательную активность, сочетание различных форм коллективной и индивидуальной работы на уроке и максимальную самостоятельность в учении учащихся. 5. Реализация на уроке всех дидактических принципов. 6. Создание условий для успешного учения учащихся. 43 Психологические требования 1. Психологическая цель урока: 1) проектирование развития учащихся в пределах изучения конкретного учебного предмета и конкретного урока; 2) учет в целевой установке урока психологической задачи изучения темы и результатов, достигнутых в предшествующей работе; 3)продумывание отдельных средств психолого-педагогического воздействия, методических приемов, обеспечивающих развитие учащихся. 2. Стиль урока: 1) определение содержания и структуры урока в соответствии с принципами развивающего обучения: соотношение нагрузки на память учащихся и их мышление; определение объема воспроизводящей и творческой деятельности; планирование усвоение знаний в готовом виде (со слов учителя, из учебника, пособия и т. п.) и в процессе самостоятельного поиска; выполнение учителем и учащимися проблемно-эвритического обучения; учет контроля, анализа и оценки деятельности школьников, осуществляемых учителем, а также взаимной критической оценки, самоконтроля и самоанализа учащихся; соотношение побуждения учащихся к деятельности (комментарии, вызывающие положительные чувства в связи с проделанной работой, установки, стимулирующие интерес, волевые усилия к преодолению трудностей и т. д.); 2) особенности самоорганизации учителя: педагогический такт (случаи проявления); психологический климат на уроке (поддержание атмосферы радостного, искреннего общения, деловой контакт и др.). 44 Психологические требования 3. Организация познавательной деятельности учащихся: 1) определение мер для обеспечения условий продуктивной работы мышления и воображения учащихся; 2) организация деятельности мышления и воображения учащихся в процессе сформирования новых знаний и умений; 3) закрепление результатов работы: формирование навыков путем упражнений, обучение переносу ранее усвоенных умений и навыков на новые условия работы, предупреждение механического переноса. 4. Организованность учащихся: 1) отношение учащихся к учению, их самоорганизация и уровень умственного развития; 2) возможные группы учащихся по уровню обучаемости, учет этих обстоятельств при определение сочетания индивидуальных, групповых и фронтальных форм работы учащихся на уроке. 5. Учет возрастных особенностей учащихся: 1) планирование урока в соответствии с индивидуальными и возрастными особенностями учащихся; 2) дифференцированный подход к учащимся. 45 Методические требования 1.Точное и творческое выполнение программнометодических требований к уроку; грамотное определение типа урока, его место в теме, в системе внутри курсовых связей, ведение особенностей каждого урока. 2.Учет обученности, обучаемости, реальных возможностей учащихся конкретного класса. Обязательный учет интересов, склонностей и потребностей учащихся. 3. Продумывание и решение в единстве задач образования, развития и воспитания. 4. Специальный выбор типа, структуры и темпа проведения урока, обеспечивающих реализацию поставленных задач и экономного использования времени. 5. Концентрация внимания школьников на главном, существенном. 6. Безусловное обеспечение практической направленности учебного процесса, создание реальных возможностей, применением учащимися полученных знаний, не допуская формального усвоения теоретических сведений. 7. Расширение арсенала методов обучения за счет знаний их системной классификации. Формирование у всех школьников активного отношения к учебной работе. 8. Сочетание фронтальных, групповых, коллективных и индивидуальных форм работы. 9. Осуществление на основе диагностики учебных возможностей, дифференцированного подхода к учащимся, когда дифференциация не только и не сколько объем и содержание образования, дифференциация меры и специфики помощи школьникам. 11. Общение с учащимися на основе сочетания высокой требовательности с уважением к личности школьника. 12. Использование ТСО только с точки зрения их целесообразности. 13. Непременное создание благоприятных дел работы на уроках гигиены и эстетических условий. 14. Четкое следование замыслу плана урока и одновременная готовность перестраивать его ход при изменении учебной ситуации. 46 Виды анализа урока Виды анализа Комплексный анализ Структурный анализ Краткий анализ Аспектный анализ Характеристика вида Всесторонний анализ, позволяющий рассматривать в единстве и взаимосвязи основные характеристики урока - цели, содержание обучения, средства и методы обучения, организацию деятельности на уроке и основные структурные элементы урока. Анализ урока с позиции построения его структуры, обоснованности и необходимости выбора определенного этапа урока в целях реализации основной цели урока. Анализируется каждый этап урока, рассматриваются его полезность и значимость в общей структуре учебного занятий. Анализ всех компонентов урока на реализацию основной цели урока, соответствие формы, средств, содержания урока, цели урока. Глубокое рассмотрение урока по одному направлению, основанию, аспекту. Аспекты анализа бывают разнообразными. Укажем некоторые из них: реализация цели урока, формирование учебных умений и навыков учащихся соответствие учебного материала содержанию и требованиям программы и др. 47 Схема структурного анализа 1. Общие сведения: дата, класс, школа, фамилия, имя, отчество учителя, тема учебной программы, тема урока, обзор средств обучения и учебной среды (оборудование кабинета, его устройство, состояние и т. д.) 2. Соблюдение ТБ и санитарно-гигиенических норм. 3. Затраты времени учителя на подготовку к уроку, готовность средств к конкретному уроку их соответствие теме, содержание раздаточного материала, инструкции вопросов к ним. Структура урока 4. Организационный этап. Подготовка учащихся к работе на уроке. Взаимные приветствия учителя и учащихся, фиксация отсутствующих, проверка состояния кабинета. 5. Этап проверки домашнего задания. Выяснить степень усвоения заданного на дом материала, определение типичных недостатков в знаниях и их причины, ликвидация обнаруженных недостатков. 6. Этап всесторонней проверки знаний. Проверка различными методами объема и качества усвоенного материала, проверка степени сформулированности обще учебных навыков и умений, проверка характера мышления учеников, комментирование ответов учащихся, оценка знаний умений и навыков. 7. Этап подготовки учащихся к активному и сознательному усвоению нового материала. Сообщение темы, цели и задач изучения нового материала, показ его практической значимости, постановка перед учащимися учебной проблемы. 48 8. Этап усвоения новых знаний. Организация внимания, изложение учителем нового материала, обеспечение его восприятия и осознания, систематизация и обобщение этого материала учащимися. 9. Этап проверки понимания учащимися нового материала. Проверка учителем глубины понимания учащимися материала, внутренних закономерностей и связей сущностей новых понятий. 10. Этап закрепления нового материала. Закрепление полученных знаний и умений, закрепление методики изучения материала, закрепление методики предстоящего ответа ученика при очередной проверке знаний. 11. Этап информации учащихся о домашнем задании, инструктаж по его выполнению. Информация о домашнем задании, инструктаж по его выполнению, проверка того, как учащиеся усвоили содержание работы и способ ее выполнения. Подведение итогов работы: как работал класс, кто из учащихся особенно старался, что нового узнали школьники. Комплексный анализ урока 49 это: 2. Определить 1. Проанализировать урок с учетом реализованы ли 50 Схема комплексного урока 1. Общие сведения об уроке: 2. Организация урока: 3. Структура урока: 4. Содержание урока: 5. Методы, приемы и средства обучения: 6. Учитель как личность: 7. Заключение по уроку: школа, класс, предмет, Ф.И.О. учителя, тема урока, цель, тип урока. - готовность учителя к уроку; - готовность учащихся к уроку; - подготовленность классного помещения; - мобилизующее начало урока. - этапы урока, распределение времени; - четкость этапов, выделение главного; - соответствие структуры урока целям и его содержанию; - насыщенность урока и темы; - сочетание коллективной, групповой и индивидуальной работы с учащимися. - объем фактического материала, соответствие его программе и уровню знаний учащихся; - научность изложения материала, единство образовательной и воспитательной функций; - соответствие теории и упражнений; - повторение пройденного, опорные знания; - связи внутрипредметные и межпредметные, связь с жизнью. - целесообразность методов обучения; - достижение основных принципов дидактики в обучении; - познавательная активность учащихся и роль учителя на уроке; - наличие обратной связи; - развитие логического мышления у учащихся и самостоятельность в обучении; - работа со слабоуспевающими учащимися; - методы проверки и оценки знаний учащихся; - средства достижения и поддержания внимания учащихся на уроке и интереса к предмету; - итог урока, его воспитательная ценность. - знания и методическая грамотность учителя; - культура речи и педагогический такт; - доброта и требовательность к учащимся; - контакт учителя с учащимися. - эффективность урока; - ценные стороны урока и недостатки; - предложения учителю. 51 Самоанализ урока 1. Место данного урока в системе уроков по теме или подтеме, правильность постановки цели урока. 2. Организация урока: а) тип урока; б) структура урока; его отдельные элементы, их последовательность и дозировка во времени; соответствие построения урока его содержанию и поставленной цели; в) подготовленность класса к уроку; г) организация учащихся для активной работы на протяжении всего урока; сочетание фронтальной, групповой, коллективной и индивидуальной работы на уроке; д) плотность урока; рациональное использование времени. 3. Содержание урока: а) научность материала; б) правильность подбора материала для различных этапов урока и видов деятельности учащихся; в) соответствие содержания урока требованиям программы, по которой работает учитель; г) воспитательная направленность урока; д) связь теории с практикой; раскрытие учителем практической значимости знаний; обучение учащихся применению своих знаний на практике; е) связь изучаемого материала с ранее пройденным; приемы повторения пройденного; ж) межпредметные связи; з) речь учителя: грамотность, эмоциональность, лексическое богатство; и) качество знаний учащихся, их умений и навыков; к) речь учащихся. 4. Методика проведения урока: 52 а) оборудование урока, использование наглядных пособий, дидактического материала на всех этапах урока; б) методы и приемы, применяемые учителем на каждом этапе урока; в) соответствие методов содержанию и целям урока, возрасту и уровню подготовки учащихся; эффективность применяемых методов; г) постановка учителем перед учащимися цели урока и подведение итогов; д) работа с отстающими и слабоуспевающими на уроке; е) владение учителем методами активного обучения, целесообразность применения этих методов на данном уроке; ж) система оценки знаний учащихся учителем; их педагогическая ценность 5. Общение учителя на уроке: тон, стиль отношений, манера общения с классом и отдельными детьми. 6. Работа и поведение учащихся на уроке: а) активность класса и отдельных учащихся; б) заинтересованность учащихся материалом урока; отношение к уроку; в) отношение учащихся к учителю; г) дисциплинированность и организованность учащихся; д) речь учащихся; задаваемые вопросы. 7. Общие выводы по уроку. 8. Как будет учтен опыт данного урока в вашей дальнейшей работе 53 Программа оценки эффективности урока Деятельность учителя Деятельность учащихся Расширение содержания Знания учащихся выходят за учебного материала за счет рамки традиционных. введение дополнительных понятий и углубление традиционно вводных понятий. Формируется научное Умеют раскрывать и мировоззрение. обосновывать причинноследственные связи между изученным учебным материалом. Вводятся необходимые Владеют научными научные понятия и понятиями и грамотно термины. используют научную терминологию. Используются методы Владеют и используют научного исследования и методы научного познания, методы науки изучаемого методы науки изучаемого предмета. предмета. Осуществляется интеграция Владеют и осознанно знаний из различных оперируют (смежных) областей науки. интегрированными знаниями. Обучение ведется на всех Выполняет задания любой трех условиях, но сложности, отдавая при этом преобладает третий предпочтение творческим творческий. заданиям. Используется в процессе Владеют исследовательскими обучения частично и частично поисковыми поисковый и методами, умело используют исследовательский методы. их в процессе самостоятельного поиска знаний. Обучение ведется Имеют глубокие и прочные результативно не только на знания, владеют способами их уроках, но и в ходе лекций, применения семинаров. 54 Планирование урока. Пример конспекта урока 1. Тема: ..................................................................................... Цели: Образовательные: ...................................... Воспитательные: ..... .... ...................... ................. Развивающие: ... .................... ........ ... ..... .......... ….. Межпредметные связи Средства обучения Методика проведения Содержание урока … …………….. Характеристи ка задачного материала … Кол-во времени Этап урока Количество часов: ......... Категория класса ........................ Учебные пособия, литература: .... .................... ..... ........ ……. …. …… Пример конспекта урока 2. Тема: ..................................................................................... Цели: Образовательные: ...................................... Воспитательные: ..... .... ...................... ................. Развивающие: ... .................... ........ ... ..... .......... Основное содержание учебного материала. Структура урока. Записи на доске и в Ход урока Деятельность учителя 55 Деятельность учащихся УРОВНЕВЫЙ АНАЛИЗ УЧЕБНО-ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ Репродуктивный Репродуктивнопоисковый Поисковый Уровень Умственные действия Характеристики уровня  анализ  синтез  гипотеза  мысленный  Последовательное и  анализ  синтез  сравнение  абстрагирование  аналогия  гипотеза  индукция  дедукция  мысленный эксперимент  Оптимальное сочетание различных видов УПД в зависимости от целей занятия и содержания учебного материала;  самоорганизация и самоуправление процесса усвоения знаний, приобретения умений и навыков.  анализ  синтез  абстрагирование  аналогия  индукция  дедукция  Восприятие учебного материала, его осмысление и обобщение;  выработка практических умений и навыков;  самоорганизация и самоконтроль за процессами усвоения знаний, умений и навыков. эксперимент  идеальная модель  и др. 56 самостоятельное решение познавательных задач, обеспечивающее творческое усвоение знаний;  самоуправление процессом усвоения новых знаний. Общеучебные умения и навыки Планирование учебной деятельности - осознание учебной задачи; - постановка целей; - выбор рационального и оптимального пути их достижения; - определение последовательности и продолжительности этапов деятельности; - построение модели деятельности. Организация своей учебной деятельности - рациональная организация рабочего места; - организация режима работы; - организация домашней самостоятельной работы; - определение порядка и способов умственной деятельности. Восприятие информации Мыслительная деятельность Оценка и осмысление результатов своих действий - чтение, работа с книгой, справочником, словарем, конспектирование; - библиографический поиск; - слушание, запись прослушанного; - управление вниманием; - наблюдение, запоминание. - осмысление учебного материала, выделение главного; -анализ и синтез; - абстрагирование и конкретизация; - индукция дедукция; - классификация, обобщение, систематизация; - построение рассказа, ответа, речи, доказательства, аргументирование. - самоконтроль и взаимоконтроль результатов учебной деятельности; - оценка правильности изложения материала или решения задачи; - рефлексивный анализ: «знание о знании» и «знание о незнании»; 57 МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ. МЕТОДИКА РАБОТЫ НАД ОПРЕДЕЛЕНИЕМ. Понятие - форма мышления, в которой отражены существенные (отличительные) свойства объектов изучения. Понятие считается правильным, если оно верно отражает реально существующие объекты. Содержание понятия - это множество всех существенных признаков данного понятия. Объем понятия - множество объектов, к которым применимо данное понятие. Существенные (характеристические) свойства - это такие свойства, каждое из которых необходимо, а все вместе достаточны для характеристики объектов, принадлежащих понятию. Понятие Содержание Объем Параллелогамм • противоположные стороны равны и параллельны; • противоположные углы равны; диагонали в точке пересечения делятся пополам и др. Множество четырехугольников: 1) собственно параллелограммы; 2) ромбы; 3) прямоугольники; 4) квадраты. Классификацией называется последовательное, многоступенчатое разбиение множества на два класса с помощью некоторого свойства. 58 Правильная классификация понятий предполагает соблюдение следующих условий: - классификация проводится по определенному признаку, остающемуся неизменным в процессе классификации; - понятия, получающиеся в результате классификации, взаимно независимые, т. е. ни одно из них не должно входить в объем другого класса. - сумма объемов понятий, получающихся при классификации, равняется объему исходного понятия; - в процессе классификации переходят к ближайшему в данном родовом понятии виду. Пример правильной классификации Треугольники Неравнобедренные Остроугольные Равнобедренные Неравнобедренные Прямоугольные Равнобедренные Неравнобедренные Равнобедренные Тупоугольные Равносторонние Неравносторонние 59 Виды определений Определение понятия - это предложение, в котором раскрывается содержание понятия, т.е. совокупность условий, необходимых и достаточных для выделения класса объектов, принадлежащих определяемому понятию. Аксиоматические (косвенные) определения определения исходных понятий, которые даются посредством исходных понятий некоторой теории через ее аксиомы (например: понятие площади фигуры). При аксиоматическом построении математической теории некоторые понятия остаются неопределенными( точка, прямая, плоскость). Дескрипциями называются определения математических объектов путем указания их свойств («То число, которое, будучи умножено на длину диаметра, дает длину его окружности» дескрипция числа π). Определения через род и видовые отличия – определения, в которых определяемое выделяется из предметов некоторой области, которая при этом явно упоминается в определении (род), путем указания характеристического свойства определяемого (видовое отличие). Например: «Квадрат - прямоугольник с равными сторонами». Генетические определения. Это такие определения, в которых описывается или указывается способ его происхождения, образования, возникновения, построения. Генетические определения представляют собой разновидность определения через род и видовые отличия. Например: «Сферой называется поверхность, полученная вращением полуокружности вокруг своего диаметра». Индуктивными называются определения, которые позволяют из сходных объектов (теории) путем применения к ним конкретных операций получать новые объекты. Например, по индукции вводится определение натурального числа в математике. Определение через абстракцию - определения, связанные с выделением объектов через установление между ними отношений равенства, равнозначности, тождества. В определении через абстракцию математическое понятие определяется как семейство классов эквивалентности по некоторому отношению эквивалентности. 60 Методика работы над определением. Этапы формирования понятий Упражнения, реализующие их Упражнения на применение ранее 1. Мотивация введения понятия изученного материала 2. Выделение существенных свойств понятия Упражнения практического характера Упражнения на построение объектов, удовлетворяющих указанным свойствам 3. Синтез выделенных свойств, формулировка понятия Упражнения с моделями фигур 4. Понимание смысла слов в определении понятия Упражнения на распознавание объектов, принадлежащих объему понятия. 5. Усвоение логической структуры определения понятия Упражнения на распознавание и выведение следствий. 6. Запоминание определения понятия Упражнения на составление родословной понятия 7. Применение понятия Упражнения на применение понятия в различных ситуациях 8. 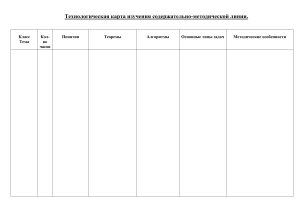Установление связей изучаемого понятия с другими понятиями Упражнения на систематизацию понятия 61 Технологическая цепочка формирования математических понятий Этапы формирования понятий 1. Мотивация введения понятия 2. Выделение существенных свойств понятия Методические приемы 1) Наблюдение с использованием различной наглядности, в результате которого выделяются общие и существенные свойства наблюдаемых объектов. 2) Опыт или практическая работа исследовательского характера, в результате которой накапливаются данные для индуктивного заключения. 3) Отыскание ярких практических примеров, показывающих необходимость введения нового понятия. 4) Выделение необходимых свойств объектов на основе моделирования и их фиксирование при помощи символов, терминов, схем и т.п. 5) Варьирование несущественных свойств объектов при сохранении существенных, что создает основу для их обобщения. 6) Обзоры изученного или исторические обзоры, показывающие корни нового в старом или аналогии нового в старом. 7) Решение задач, в ходе которого появляется необходимость введения 62 нового понятия (подводящие задачи). 3. Синтез выделенных свойств, формулировка понятия 4. Понимание смысла слов в определении понятия 5. Усвоение логической структуры определения понятия 6. Запоминание определения понятия 7. Применение понятия 8. Установление связей изучаемого понятия с другими понятиями 1) Установление для нового понятия родового понятия, его видовых отличий и характера связей между ними. 2) Формулировка определения нового понятия с введением термина, символа. 3) Решение ученых задач на «узнавание», подведение под понятие, приведение примеров и контрпримеров и т.д. 4) Текущий контроль и коррекция усвоения определения. 1) Теоретическое обобщение в форме бесед, лекций или семинаров. Использование обобщающих и классифицирующих таблиц, схем, опорных конспектов. 2) Установление с помощью решения соответствующих учебных задач связей между понятиями, составление родословной понятия, обобщение и специализация понятий и т.д. 3) Решение задач на применение понятия и систем понятий. 63 Составление родословной понятия Пример родословной понятия «Отрезок» Отрезок Прямая Точка Лежать между Точка Прямая ТЕОРЕМА. ВИДЫ ТЕОРЕМ. МЕТОДИКА РАБОТЫ НАД ТЕОРЕМОЙ Теоремой называется математическое истинность которого устанавливается доказательства. 64 предложение, посредством Виды формулировок теорем Категорическая Условная Отношение площадей подобных фигур равно квадрату коэффициента подобия. Если фигуры подобны, то отношение их площадей равно квадрату коэффициента подобия. условие заключение Теоремы, выражающие достаточные условия понятия, называются теоремами-признаками. Теоремы, выражающие необходимые условия понятия, выражающие свойства понятия, называются теоремамисвойствами. Теоремы, содержащие необходимые и достаточные условия описывают характеристические свойства объекта, которыми можно заменить его определение. А ⇒ В – прямая теорема, В ⇒ А – обратная теорема, А ⇒ В – противоположная теорема, В ⇒ А – контрапозитивная (обратная противоположной или противоположнообратная). Рассуждение с целью обоснования истинности какого-либо утверждения называется доказательством. 65 Метод доказательства - это способ связи аргументов при переходе от условия к заключению суждения. ДОКАЗАТЕЛЬСТВО Тезис. Форма выражения тезиса – суждение. Аргументы (основания) доказательства - положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов - суждения. Apгументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы. Демонстрация - логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису. 66 Классификация методов доказательства по пути обоснования тезиса Методы доказательства Прямые Косвенные Прием преобразования условия (синтетический) Метод от противного Прием преобразования заключения (восходящий анализ) Разделительный метод или метод исключения предложений Прием преобразования заключения (нисходящий анализ) Прием последовательного преобразования то условия, то заключения Классификация методов доказательства по математическому аппарату, используемому при доказательстве 1. Метод геометрических преобразований. 2. Алгебраические методы (уравнений, неравенств, тождественных преобразований). 67 3. Векторный метод, использующий аппарат векторной алгебры. 4. Координатный метод. Организация работы над теоремой 68 Этапы работы над теоремой 1. Мотивация изучения теоремы 2. Ознакомление с теоремой 3. Усвоение содержания теоремы 4. Запоминание формулировки теоремы 5. Ознакомление со способом доказательства 6. Доказательство теоремы 7. Применение теоремы 8. Установление связей изучаемой теоремы с изученными ранее Упражнения, реализующие их Упражнения на оперирование с моделями фигур и измерение величин Упражнения с практическим содержанием Упражнения на применение ранее изученных теорем и понятий Упражнения на выделение условия и заключения теоремы Упражнения на распознавание ситуаций, удовлетворяющих теореме Упражнения на выполнение чертежей моделирующих условие теоремы Упражнения на ознакомление с методом доказательства Упражнения, моделирующие способ доказательства Упражнения на выделение в доказательстве недостающих утверждений и их обоснований Упражнения на систематизацию теорем Упражнения на составление «родословной» теоремы Упражнения на составление плана доказательства теоремы Упражнения на составление алгоритмов 69 Технологическая цепочка изучения теоремы Этапы изучения Методические приемы теоремы 1) Обзор потребности практики или других исторических причин, 1. Мотивация изучения теоремы приводящих к появлению данного утверждения. 2) Решение задач исторического и практического характера. 3) Практическая или лабораторная работа исследовательского характера, приводящая к новому утверждению. 4) Повторение понятий и теорем, на которые будет опираться новая теорема или ее доказательство. 5) Решение задач на применение ранее изученных теорем связанных с данной. 1) Выделение условия и заключения 2. Ознакомление с теоремы. теоремой 2) Иллюстрация содержание теоремы на чертеже или на модели. 3. Усвоение 3) Краткая запись содержания, с содержания теоремы использованием обозначений на чертеже и символики. 4. Запоминание 4) Анализ логической структуры формулировки теоремы. теоремы 5) Рассмотрение частных и особых случаев, если они существуют. 1) Рассмотрение примеров, убеждающих 5. Ознакомление в необходимости доказательства. со способом 2) Решение задач близких по методу доказательства решения к данной теореме, «наводящих» на метод доказательства. 3) Повторение ранее изученных теорем, связанных с новой теоремой или ее доказательством. 70 4) Изучение и осмысление чертежа, с целью установления связей между его элементами. 5) Составление плана доказательства. 1) Реализация этапов доказательства 6. Доказательство согласно плану. теоремы 2) Выстраивание цепочки доказательства с логическим обоснованием отдельных умозаключений. 3) Проверка правильности использования символики и других записей. 1) Построение «родословной теоремы». 7. Применение 2) Показ места и роли теоремы в новой теоремы теме на основе систематизации и классификации. 8. Установление связей изучаемой 3) Выведение следствий из теоремы, теоремы с доказательство частных случаев. изученными ранее 4) Рассмотрение практических приложений теоремы. 5) Решение задач на применение теоремы и метода ее доказательства. 6) Доказательство теорем, связанных с данной (обратной, противоположной, аналогичной), сформулированных в виде задачи на доказательство. 7) Обобщение теоремы, метода доказательства и его основной идеи. 8) Анализ и обобщение типов задач, решаемых с помощью теоремы или метода ее доказательства. 71 ЗАДАЧИ В ОБУЧЕНИИ МАТЕМАТИКЕ Различные определения понятий «задача» и «проблема» Автор Формулировки понятий «задачи» и «проблема» 1 2 Педагогическая Задача характеризуется наличием у энциклопедия, учащихся определенной цели, т.2 – М.: стремлением получить ответ на тот Советская или иной вопрос, достичь желаемого энциклопедия, результата с учетом имеющихся 1965. условий и требований. Психологический Задача (проблема) – цель деятельности словарь/ под. ред. данная в определенных условиях и В.В. Давыдова. – требующая для своего достижения М.: Педагогика, использование адекватных этим 1983. условиям средств. Процесс решения – поиск и применение этих средств. В. Оконь О.К. Тихомиров, Проблема не есть то же самое, что и задача. … Проблемный характер для данного индивида имеют лишь такие задачи, в которых содержится определенная практическая или теоретическая трудность, требующая исследовательской активности приводящей к решению. Задача выступает как объект, как предмет мыслительной работы человека. Как правило, это не отдельный предмет, а целая предметная ситуация. Задачу характеризуют также соотношения между условиями и требованиями. 72 1 С.Л. Рубинштейн Г.Д. Бухарова Г.А. Балл Л.Л. Гурова 2 Задача… заключает в себя цель для мыслительной деятельности индивида, соотнесенную с условиями, которыми она задана. Под задачей будем подразумевать объект мыслительной деятельности, в котором в дидактическом единстве представлены составные элементы (предмет, условие, требование) и получение некоторого познавательного результата возможно при раскрытии отношения между известными и неизвестными элементами задачи. Термин «задача» употребляется для обозначения объектов относящихся к трем различным категориям: 1) к категории цели действия субъекта, требования, поставленного перед субъектом; 2) к категории ситуации, включающей наряду с целью условия в которых она должна быть достигнута; 3) к категории словесной формулировки этой ситуации. Задача – объект мыслительной деятельности, содержащий требования некоторого практического преобразования или ответа на теоретический вопрос посредством поиска условий, позволяющих раскрыть связи (отношения) между известными и неизвестными ее элементами. 73 1 М. Ю. Колягин В.И.Крупич М.Н. Скаткин 2 Задача – совокупность компонентов ACRB: - начальное состояние (А) характеризует условие конкретной задачи; - конечное состояние (В) характеризует частный результат решения задачи; решение задачи (R) характеризует способ преобразования условия для получения, требуемого результата; базис решения (С) характеризует объем теоретических или практических знаний, необходимых для решения задачи. Задача – замкнутая система S = {A, C, R, D, B}: А – условие задачи, то есть данные и отношения между ними; В – требование задачи, то есть искомые и отношения между ними; R – основные отношения между данными и искомыми; D – способ, определяющий процесс решения задачи, то есть способ действия по преобразованию условия задачи для нахождения искомого; С – базис решения задачи, то есть теоретические основы, необходимые для обоснования решения. В основе всякой задачи лежит противоречие между тем, что есть и тем, чего человек хочет добиться. Это противоречие и движет мысль вперед. 74 1 А.М. Матюшкин Г.И. Саранцев 2 Задача – способ знакового предъявления задания одним человеком другому (или самому себе), включающий указания на цель и условия его достижения. В интеллектуальной задаче цель действия составляет искомое, выраженное вопросом. Решение интеллектуальной задачи составляет процесс преобразование условий, направленных на достижение искомого. Задача проблемная требует для достижения искомого обнаружения таких новых отношений, которые не даны в условиях задачи, или таких способов преобразования заданных условий, которые не известны учащемуся. При решении такой задачи у учащегося возникает потребность в неизвестных новых знаниях или способах действия. Задача – многоаспектное явление обучения, занимающее большое место в учебном процессе и выступающее способом организации и управления учебно-познавательной деятельности учащихся, носителем действий адекватных содержанию обучения математике, средством целенаправленного формирования знаний, умений и навыков, одной из форм методов обучения, средством связи теории с практикой. 75 Д. Пойа 1 А.Н. Леонтьев Л.Ф. Спирин Л.М. Фридман А.Ф. Эсаулов Л.М. Лоповок 2 …задача предполагает необходимость сознательного поиска соответствующего средства для достижения ясно видимой, но непосредственно недоступной цели. Задача есть цель, данная в определенных условиях (в конкретной ситуации). Задача – это результат осознания субъектом действий, цели действий, условий действий и проблемы решения задачи. Задача определяется как модель проблемной ситуации, выраженной с помощью знаков некоторого естественного или искусственного языка. Задача – это более или менее определенные системы информационных процессов, несогласованное или даже противоречивое отношение между которыми вызывает потребность в их преобразовании. Математической задачей называют требование осуществить некоторую математическую деятельность в указанных условиях. Проблемная задача характерна тем, что алгоритм ее решения до начала решения неизвестен, трудно даже установить, достаточно ли наших знаний для выполнения задания. Главная задача - открыть способ решения и убедиться в его пригодности. 76 Учебная и познавательная задачи Автор 1 Д.Б. Эльконин Г.А. Балл [19]: различает понятия учебной и познавательной задачи О.Б. Епишева Особенности учебной и познавательной задачи 2 Специфика учебной задачи заключается в том, что ее цель и результат состоят в изменении самого субъекта деятельности, а не в изменении предмета деятельности. 1) познавательные задачи решаются не только в ходе учебной деятельности, и, значит, только некоторые познавательные задачи являются учебными; 2) среди учебных задач основную массу составляют познавательные задачи, некоторые познавательными не являются (коммуникативные, двигательные и др.); 3) всякая специфическая учебная задача направлена на овладение общим способом решения всех задач определенного класса и поэтому может быть интерпретирована как познавательная. Одна и та же предметная задача может служить достижению нескольких конкретных учебных целей и, следовательно, быть компонентом нескольких учебных задач. В то же время та или иная конкретная учебная цель может быть достигнута несколькими предметными задачами 77 Процесс решения задачи Автор, источник 1 О.К. Тихомиров В.А. Далингер Понимание процесса решения задачи 2 Реальное решение задачи, – это всегда взаимодействие субъекта и объекта, в ходе которого преобразуется не только задача, объект мышления, но и сам субъект Процесс решения любой математической задачи может быть исследован с различных точек зрения: а) с математической – какова последовательность действий и как их надо совершить над данными задачи, чтобы найти искомое; б) с логической – устанавливается, из каких логических операций состоит процесс решения задачи; в) с психологической – в чем состоят психологические особенности решения задачи; г) с педагогической – определяются приемы, которые помогут ученику самостоятельно найти решение; д) с информационной – устанавливается возможность решения задачи посредством компьютера. 78 1 Л.М. Фридман, Е.Н. Турецкий 2 Решить математическую задачу – это значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения), получает то, что требуется в задаче, − ее ответ» Авторы выделяют восемь этапов в процессе решения задачи: - анализ задачи; - построение модели задачи; - поиск способа решения задачи; - осуществление решения задачи; - проверка решения задачи; - исследование задачи; - формулирование ответа задачи; - познавательный анализ задачи и ее решения. 79 Решение задач с позиции деятельностного подхода Этап решения Ориентировочный Содержание этапа 1. Восприятия условия задачи 2. Анализ условия задачи 3. Воспроизведение (восполнение) необходимых для решения знаний 4. Прогнозирование процесса поиска и его результатов, формулирование гипотезы 5. Составление плана решения Исполнительский 6. Попытка решения задачи на основе известных способов 7. Переконструирование плана решения, нахождения нового способа 8. Решения задачи другими способами 9. Проверка решения, доказательство его правильности Контрольно10. Оценка рациональности и систематизирующий эффективности выбранного варианта решения 11. Введение полученного знания в имеющуюся у обучаемого систему знаний, представлений, отношений 12. Выход на новые проблемы 80 Суждения умозаключения, … Обобщение Классифика Продукты мышления Синтез Мышление Проблемные ситуации, противоречия Анализ Сравнение Формы реализации Результат Приемы Процесс Условия возникновения Процесс решения задачи Формулы, чертежи, схемы … Конкретиза ··· 81 ··· Д. Пойа. Как решать задачу. Львов: журнал «Квантор», 1991. – с. 210 – 212. Как решать задачу ПОНИМАНИЕ ПОСТАНОВКИ ЗАДАЧИ I Что неизвестно? Что дано? В чем Нужно ясно состоит условие? понять Возможно ли удовлетворить условию? задачу Достаточно ли условие для определения неизвестного? Или недостаточно? Или чрезмерно? Или противоречиво? Сделайте чертеж. Введите подходящие обозначения. Разделите условие на части. Постарайтесь записать их. СОСТАВЛЕНИЕ ПЛАНА РЕШЕНИЯ II Не встречалась ли вам раньше эта Нужно найти задача? Хотя бы в несколько другой форме? связь между Известна ли вам какая-нибудь родсданными и твенная задача? Не знаете ли теоремы, неизвестным. которая могла бы оказаться полезной? Если не удаРассмотрите неизвестное! И постается сразу райтесь вспомнить знакомую задачу с тем обнаружить же или подобным неизвестным. эту связь, Вот задача, родственная с данной и возможно, уже решенная. Нельзя ли воспользоваться полезно бу- ею? Нельзя ли применить ее результат? дет рассмот- Нельзя ли использовать метод ее решения? реть вспомо- Не следует ли ввести какой-нибудь гательные вспомогательный элемент, чтобы стало задачи. В ко- возможно воспользоваться прежней нечном счете задачей? необходимо Нельзя ли иначе сформулировать задачу? прийти к Еще иначе? Вернитесь к определениям. плану решеЕсли не удается решить данную задачу, ния. попытайтесь сначала решить сходную. 82 III Нужно осуществить план решения. Нельзя ли придумать более доступную сходную задачу? Более общую? Более частную? Аналогичную задачу? Нельзя ли решить часть задачи? Сохраните только часть условия, отбросив остальную часть: насколько определенным окажется тогда неизвестное! как оно сможет меняться? Нельзя ли извлечь что-либо полезное из данных? Нельзя ли придумать другие данные, из которых можно было бы определить неизвестное? Нельзя ли изменить неизвестное, или данные, или, если необходимо, и то и другое так, чтобы новое неизвестное и новые данные оказались ближе друг к другу? Все ли данные вами использованы? Все ли условия? Приняты ли вами во внимание все существенные понятия, содержащиеся в задаче? ОСУЩЕСТВЛЕНИЕ ПЛАНА Осуществляя план решения, контролируйте каждый свой шаг. Ясно ли вам, что предпринятый вами шаг правилен? Сумеете ли доказать, что он правилен? ВЗГЛЯД НАЗАД (изучение полученного решения) IV Нужно изучить найденное решение. Нельзя ли проверить результат? Нельзя ли проверить ход решения? Нельзя ли получить тот же результат иначе? Нельзя ли усмотреть его с одного взгляда? Нельзя ли в какой-нибудь другой задаче использовать полученный результат или метод решения? Д. Пойя. Как решать задачу. Львов: журнал «Квантор», 1991. – с. 83 – 85. Сравнение задач на нахождение и задач на доказательство 83 Задачи на нахождение Цель «задачи на нахождение» — определить какой-нибудь элемент, неизвестное задачи. Неизвестное также называется «quaesitum» или «искомое», или «то, что требуется найти». «Задачи на нахождение» могут быть теоретическими или практическими, отвлеченными или конкретными, серьезными или всего лишь развлекательными головоломками. Искомыми могут быть всевозможные неизвестные. От нас может потребоваться найти, получить, приобрести, произвести или построить всякого рода объекты. Задачи на доказательство «Задачи на доказательство» имеют своей целью доказать, что определенное четко сформулированное утверждение верно или же неверно. От нас требуется ответить на вопрос: данное утверждение верно или неверно? В заключение своего решения мы должны получить окончательный ответ, доказав справедливость утверждения или его ошибочность. Главными элементами Если «задача на «задачи на нахождение» доказательство» является являются неизвестное, математической задачей данные и условия. обычного типа, то ее главными частями являются предпосылка (hypothesis) и заключение (conclusion) теоремы, которую мы должны доказать или опровергнуть. 84 Если вы хотите решить «задачу на нахождение», вы должны знать, и при том совершенно точно, ее главные элементы — неизвестное, данные и условия. В нашей таблице представлено много вопросов и советов, связанных с этими элементами. Что неизвестно? В чем состоит условие? Что дано? Разделите условие на части. Найдите связь между данными и неизвестными. Рассмотрите неизвестное! И постарайтесь припомнить знакомую задачу с тем же или подобным неизвестным. Сохраните только часть условий, отбросив остальные; в какой мере 85 [Не все математические теоремы могут быть естественным образом разбиты на предпосылку и заключение. Так, например, вряд ли возможно таким образом разделить следующую теорему: «Количество простых чисел бесконечно».] Если вы хотите решить «задачу на доказательство», то должны знать, и при том совершенно точно, ее главные элементы — предпосылку и заключение. В нашей таблице имеются полезные вопросы и относительно этих элементов задачи, но у нас они приспособлены к «задачам на нахождение». Соответствующие вопросы и советы к «задачам на доказательство» будут: В чем состоит предпосылка? Каково заключение? Расчлените предпосылку на части. Найдите связь между предпосылкой и заключением. Рассмотрите заключение. Постарайтесь припомнить знакомую задачу с тем же или подобным заключением. теперь определяется неизвестное? Как можно его варьировать? Сумеете ли вы вывести что-нибудь полезное из данных? Сможете ли вы придумать другие данные, из которых можно было бы определить неизвестное? Сможете ли изменить неизвестное или данные, а если необходимо — и то и другое, чтобы новое неизвестное и новые данные стали ближе друг к другу? Все ли данные вы использовали? Все ли условия вы использовали? Сохраните только часть предпосылки, отбросив остальные. Заключение по-прежнему обоснованно? Сможете ли вы вывести что-нибудь полезное из предпосылки? Сможете ли вы придумать другую предпосылку, из которой смогли бы легко вывести такое заключение? Сможете ли вы изменить предпосылку или заключение, а если необходимо и то и другое вместе, чтобы новая предпосылка и новое заключение стали ближе друг к другу? Использовали ли вы всю предпосылку? Различные классификации задач Основания для Типы задач классификации 86 1 По характеру объектов По характеру требований По отношении к теории По особенностям условия По ведущим функциям в обучении По отношении к теории По отношению к учебнопознавательной деятельности 1 2 1) практические; 2) математические, (физические,…., межпредметные). 1) задачи на нахождение искомых (вычисление); 2) задачи на преобразование; 3) задачи на доказательство; 4) задачи на построение; 5) задачи на объяснение. 1) стандартные; 2) нестандартные. 1) правильные задачи; 2) задачи с противоречивыми данными; 3) задачи с лишними данными; 4) задачи с недостающими данными. 1) задачи с дидактическими функциями; 2) задачи с познавательными функциями; 3) задачи с развивающими функциями. 1) стандартные; 2) нестандартные. 1) задачи, стимулирующие учебнопознавательную деятельность; 2) задачи, организующие учебнопознавательную деятельность; 3) задачи, в процессе решения которых осуществляется контроль и самоконтроль эффективности учебнопознавательной деятельности 2 87 1) репродуктивные задачи – задачи на простое воспроизведение изученного; 2) алгоритмические задачи решаются по алгоритму, заданному в виде формулы, правила и т.д.; 3) трансформированные задачи – решаются на основе известных формул в новых ситуациях; 4) творческо-поисковые задачи – решаются на основе творческого сочетания мыслительных операций. 1) словесное описание – графическое По форме изображение; выражения 2) графическое изображение – условия задачи и словесное описание; ответа к ней 3) аналитическое задание – словесное описание; 4) словесное описание – аналитическое задание; 5) графическое изображение – аналитическое задание; 6) аналитическое задание – графическое изображение; 7) словесное описание – словесное описание; 8) графическое изображение − графическое изображение; 9) аналитическое задание – аналитическое задание. 1) алгоритмические; По степени 2) полуалгоритмические; проблемности и 3) эвристические; творчества 4) проблемные задачи; 5) исследовательские задачи; 6) творческие задачи. Функции задач в обучении математике 88 По ведущей деятельности Мотивационная Обучающая Развивающая Методологическая Управляющая Привлечение внимания ученика к вопросу, задаче, учебной теме, возбуждение познавательного интереса, актуализация посильного познавательного затруднения, преодоление которого активизировало бы мыслительную деятельность обучаемых. Углубление, систематизацию и обобщение ранее изученного материала, выделение отдельных сторон повторяемого материала для более глубокого осмысления и запоминания сделанных выводов, установление новых (отсутствующих в учебнике) Обеспечение полноты процедур учебнопознавательной деятельности учащихся, в том числе и творческой, что предусматривает самостоятельный перенос ранее усвоенных знаний и умений в новую ситуацию, видение новой проблемы в знакомой ситуации, видение новой функции объекта, осознание структуры объекта, поиск альтернативных способов решения, комбинирование ранее известных способов действий и т.п. Показ образцов научных методов познания. Усвоение учащимися знаний и 89 способов деятельности, детерминированное системой задач. 90 Типы учебнотворческих задач Виды учебнотворческих задач Развиваемые компоненты творческих способностей личности 1 2 задачи с явно выраженным противоречием 3 задачи-проблемы; задачи-парадоксы; задачи-антимонии 4 выделение противоречия, способность формулировать проблему, диалектичность мышления задачи с некорректно представленной информацией задачи с недостающей исходной информацией; задачи с избыточной информацией; задачи с противоречивой информацией; задачи, в которых практически отсутствует исходная информация, а есть только цель деятельности способность находить нужную информацию и переносить ее, применять в условиях задачи Полнота исходной информации Проблемность Признак, основание для классификации Классификация учебно-творческих задач в связи их использованием для развития творческих способностей личности В.А. Андреева, [9] 91 2 задачи на прогнозирование 3 на прогрессивные экстраполяции; на регрессивные экстраполяции; на непосредственное выдвижение гипотезы 4 способность генерировать идеи, выдвигать гипотезы задачи на оптимизацию задачи на выбор оптимального решения; задачи на оптимизацию процесса, функционирования объекта; задачи на оптимизацию затрат, средств деятельности гибкость, рационализм мышления задачи на обнаружение противоречия и формулировку проблемы задачи скрытого вопроса; задачи на конструирование задачных ситуаций; задачи на обнаружение мнимых противоречий; задачи на формулировку проблемы способность видения проблем и противоречий Усмотрение противоречия, формулировка задачи Оптимизация Прогнозирование 1 92 Инверсия Переформулировка задачи Разработка алгоритмических и эвристических предписаний Рецензирование 1 2 задачи на рецензирование 3 задачи на обнаружение ошибок; задачи на проверку результата; задачи на оценку процесса и результата 4 критичность мышления, способность к оценочным суждениям задачи на разработку алгоритмов и эвристических предписаний задачи на разработку алгоритма; задачи на выявление эффективных эвристик; задачи на разработку эвристических предписаний, правил способность к обобщению и свертыванию мыслительных операций, способность к рефлексии мышления задачи на коррекцию поставленной задачи задачи на уточнение цели; задачи на уточнение условий; задачи на уточнение требований и ограничений способность формулировать и переформулировать задачи задачи – «обороты» противоположны е некоторой данной задачи на поиск способа решения, который противоположен наиболее очевидному; задачи, требующие рассмотрения от конца к началу способность преодолеть инерцию мышления, способность к широкому переносу знаний и умений 93 Процедуры управления Применение принципов и методов научного познания 1 2 Исследовательские задачи, задачи на применение методов научного познания 3 экспериментальные задачи; задачи на моделирование; задачи графические; задачи на формализацию; применение математических методов; задачи на применение принципа систематичности, дополнительности, историзма и т.д. 4 способность к широкому переносу принципов, методов научного познания в новые ситуации задачи на управление задачи на выработку целей, стратегий деятельности; задачи на планирование деятельности; задачи на организацию деятельности; задачи на нормирование времени деятельности; задачи на оценку результатов деятельности способность к самоуправлению в учебнотворческой деятельности 94 2 задачи на изобретение Доминирование соответствующих процессов общения в решении творческих задач Доминирование соответствующих логических процедур деятельности Изобретение 1 задачи логические Коммуникативно-творческие 3 задачи на изобретение новых конструкций; задачи на изобретение новых способов деятельности; задачи на изобретение новых веществ задачи на описание явлений, процессов; задачи на определение понятий; задачи на объяснение; задачи на доказательство; задачи на установление причинноследственных связей задачи на распределение обязанностей в процессе коллективной творческой деятельности; задачи на поиск средств взаимопомощи и сотрудничества; задачи на поиск средств взаимоконтроля 95 4 способность к изобретательской деятельности интеллектуальные логические способности Коммунмкативнотворческие способности Конструирование 1 2 Конструкторские задачи 3 задачи на поиск нового конструкторского решения: а) на расчленение объекта; б) на синтез нескольких объектов; в) на замещение одного из элементов другим; г) использование аналога в конструировании нового объекта; д) опора на новое физическое, химическое явление; е) опора на новую физическую, химическую, технологическую идею, закономерность в решении «старой» конструкторской задачи 96 4 способности к конструированию РАЗДЕЛ 2. ЧАСТНАЯ МЕТОДИКА Основные содержательно-методические линии школьного курса математики 1. Числа, числовые множества, вычисления. 2. Тождественные преобразования выражений. 3. Уравнения, неравенства и их системы. 4. Функции и графики. 5. Элементы теории вероятностей и математической статистики. 6. Геометрическая линия. МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИЗУЧЕНИЯ ЧИСЛОВЫХ МНОЖЕСТВ И ДЕЙСТВИЙ НАД ЧИСЛАМИ Общая цель изучения: формирование у учащихся знаний о числах и действиях с ними, вычислительных умений и их использования для решения практических задач, вычислительной и алгоритмической культуры.      Этапы расширения понятия числа 5 класс – расширение понятия числа с помощью введения десятичных дробей; 6 класс - введение отрицательных целых, а затем и отрицательных дробных чисел; 8 класс - множество рациональных чисел расширяется до множества действительных чисел, для чего впервые формируется представление о рациональном числе, после изучения темы «Квадратные корни»; 9 класс с углубленным изучением математики – вводится понятие комплексного числа 97 Категории целей Знание Понимание Учебные цели числовой линии. Примеры обобщенных типов целей I уровень II уровень III уровень Термины, способы записи и чтения чисел и действий над ними, частные приемы вычислений. Определение всех видов чисел и формулировки их свойств, связи между ними, способы записи чисел, обобщенные приемы вычислений, приемы контроля вычислений. Ученик интерпретирует свойства, правила и алгоритмы действий, используя буквы, схемы и таблицы, приводит контрпримеры, подводит под понятия, различает определения и свойства чисел, выделяет ситуации применимости приемов вычислений. Схема развития понятия числа, свойства числовых множеств, обоснование свойств и правил действий, искусственные приемы вычислений, приемы их переноса и прикидки результата. Ученик воспроизводит термины, формулировки правил действий и свойств чисел, алгоритмы и частные приемы выполнения действий, приво-дит примеры для иллюстрации свойств и правил. 98 Ученик преобразует словесный и числовой материал в буквенные выражения и обратно, используя обобщенные связи между числами и приемами вычис-лений, выводит следствия, выделяет идеи и методы рассуждений, перестраивает известные и находит новые приемы решения задач. Умения и навыки Умения записывать и читать числа и числовые выражения, решать простейшие задачи по алгоритмам и частным приемам, по образцу и с помощью учителя. Умения решать задачи, самостоятельно исползуя алгоритмы, приемы вычислений, приемы прикидки и контроля, составлять числовые и буквенные выражения по условию задач. Умения решать нестандартные задачи, самостоятельно выбирать и использовать обобщенные приемы и средства рациональных вычилений и их контроля, решать задачи на доказательство, самостоятельно составлять задачи по заданному числовому и буквенному выражению. Технологическая цепочка изучения числовых множеств. 99 Для изучения каждого числового множества учителю совместно с учащимися необходимо выполнить действия, определяемые не только психологическими, но и математическими закономерностями, а также и историей развития математики: Установление на специально подобранных задачах недостаточности для их решения известного на данном этапе числового множества и вывод о необходимости расширения множества путем введения новых чисел. Доказательство того, что невозможность решения этих задач связана с невыполнимостью какого-либо действия в известном числовом множестве и вывод о том, что расширение числового множества путем введения новых чисел должно быть таким, чтобы в расширенном множестве выполнялось то действие, которое ранее было не выполнимо. Введение новых чисел, их название и определение. Объединение ранее известного числового множества и множества новых чисел в одно, его название и определение. Иллюстрация того, как соотносятся ранее известные множества с вновь введенным. Введение действий и операций над числами как элементами нового множества и выведения из них правила действий. Решение упражнений на все действия над числами; выделение в явном виде алгоритмов и приемов вычислений, их частных случаев; подтверждение выполнимости в новом числовом множестве известных законов действий. Решение задач, поставленных на первом этапе и других задач. Выявление алгебраической числового множества. 100 и порядковой структуры Специальные приемы решения задач по теме Нахождение числового значения буквенного выражения Выполнение действий и вычисление значений числового выражения Тип задачи Алгоритм выполнения приема 1. Выявить характер данных чисел (точные, приближенные). 2. Подумать, нельзя ли использовать для упрощения и рационализации вычислений законы действий или тождественные преобразования выражений. 3. Выбрать наиболее рациональный способ выполнения действий или их сочетание. 4. Установить порядок действий. 5. Выполнить действия в установленном порядке, используя алгоритмы, частные приемы или правила вычислений. 6. Выбрать способ проверки и проверить вычисления. 7. Проверить верность записи вычислений. 1. Изучить особенности данного выражения и характер числовых данных. 2. Установить, можно ли упростить выражение до подстановки числовых значений букв или после подстановки. 3. Выполнить упрощение и подстановку числовых значений. 4. Выполнить вычисления, соблюдая порядок действий и соответствующие приемы вычислений. 5. Записать ответ. 101 МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИЗУЧЕНИЯ ЛИНИИ ТОЖДЕСТВЕННЫХ ПРЕОБРАЗОВАНИЙ ВЫРАЖЕНИЙ Общая цель изучения: формирование у учащихся техники тождественных преобразований и умений использования их для решения различных задач алгебры и ее приложений. Схема изучения тождеств различных видов: числовое выражение числовое значение буквенного выражения простейшие преобразования буквенных выражений буквенное выражение тождественно равные выражения тождество тождественное преобразование способы тождественных преобразований Технологическая цепочка формирования обобщенных приемов тождественных преобразований выражений Изучение алгоритмов (частных приемов) выполняемых действий. Обобщение действий, связанных с конкретной постановкой задачи («Упростить выражение» или «Доказать тождество») на конкретном виде выражения: а) изучить особенности данного выражения; установить, какие из тождественных преобразований и в каком порядке нужно выполнить; выполнить преобразования и записать ответ. Обобщение действий после изучения каждого нового вида выражений и их преобразований. 102 Распределение линии тождественных преобразований по классам Содержание материала Класс Числовые выражения, целые выражения с переменными. Приведение подобных слагаемых. Буквенные выражения. Законы сложения и умножения. Преобразование выражений: раскрытие скобок, заключение в скобки Алгебраические выражения. Допустимые значения выражений. Степень с натуральным показателем и ее свойства. Степень с целым показателем. Одночлен. Подобные одночлены. Преобразования одночленов. Многочлен. Сложение и вычитание многочленов. Умножение многочленов. Разложение многочлена на множители. Формулы сокращенного умножения. Алгебраическая дробь. Основное свойство дроби. Сокращение дробей. Действия с алгебраическими дробями. Квадратные корни. Свойства квадратного корня. Преобразование выражений содержащих квадратные корни. Основные тригонометрические тождества и их применение в тождественных преобразованиях. Формулы приведения. Логарифм числа. Основные свойства логарифмов. 5 класс 6 класс 7 класс 7 класс 7 класс 8 класс 9 класс 9 класс Тригонометрия. Формулы приведения. Формулы 10 класс сложения, двойного и половинного аргумента. Формулы замены суммы или разности тригонометрических функций на произведение и обратно. Тождественные преобразования тригонометрических выражений. Доказательство тождеств. 103 Корень n-ной степени и его свойства. 11 класс Преобразование иррациональных выражений. Степень с рациональным показателем и действия над степенями. Определение и свойства логарифмов. 11 класс Преобразование показательных и логарифмических выражений. Категории целей Учебные цели изучения линии тождественных преобразований Знание 1 Примеры обобщенных типов целей I уровень II уровень III уровень 2 Термины, буквенная символика, способы записи и чтения различных видов выражений, основные тождества, правила, алгоритмы выполнения, частные приемы тождественных преобразований выражений. 3 Определения основных понятий и преобразований, связи и отношения между ними, следствия из основных тождеств, обобщенные приемы тождественных преобразований, способы решения основных типов задач. 4 Логическая основа формул и приемов составления и преобразования выражений, их связь со свойствами и правилами действий над числами, искусственные приемы тождественных преобразований выражений. 104 Умения и навыки Понимание 1 2 Ученик правильно воспроизводит термины и формулы, смысл правил тождественных преобразований и учебных заданий, алгоритмы и частные приемы их решения, иллюстрирует их примерами, составляет несложные буквенные выражения. Умения выполнять простейшие тождественные преобразования выражений, осуществлять числовые подстановки, выполнять преобразования по образцу или на основе помощи извне. 3 4 Ученик интерпретирует тождества как правила и алгоритмы действий, приводит контрпримеры, подводит выражение под понятие или формулу, понимает идею подстановки, выделяет ситуации применимости формул и приемов тождественных преобразований. Ученик преобразует словесный и наглядный материал в алгебраические выражения и обратно, используя обобщенные связи между выраженииями, выводит следствия из формул и правил, выделяет идеи и методы преобразований, перестраи-вает известные и находит новые приемы преобразований. Умения выполнять типовые преобразования в нестандартных ситуациях, самостоятельно использовать обобщенные и искусственные приемы тождественных преобразований, доказывать и выводить новые формулы, самостоятельно их использовать. Умения выражать в основных формулах одни переменные через другие, выполнять типовые преобразования в стандартных ситуациях, самостоятельно использовать формулы, алгоритмы и приемы тождественных преобразований и их контроля. 105 Упрощение выражений Специальные приемы решения задач по теме Тип Алгоритм выполнения приема задачи 1 2 1. Изучить особенности данного выражения. 2. Установить, какие из следующих тождественных преобразований нужно выполнить, чтобы привести данное выражение к простейшему виду, - общие алгебраические преобразования (раскрытие скобок, приведение подобных слагаемых, разложение на множители, приведение дробей к общему знаменателю, действия с дробями и т.п.), специальные преобразования (правила действия со степенями, корнями, логарифмами, использование тригонометрических тождеств). 3. Выполнить выбранные преобразования, используя соответствующие частные приемы. 4. Записать ответ, если нужно, упростив его. 106 Разложение выражения на множители 1. Изучить особенности данного выражения. 2. Если есть общий множитель у всех слагаемых, вынести его за скобки. 3. Рассмотреть выражение, освобожденное от общего множителя; установить, нельзя ли использовать формулы сокращенного умножения, группировку слагаемых, правила действия со степенями, с корнями, потенцирование, формулы преобразования суммы тригонометрических функций в произведение и т.д. 4. Если п. 3 не имеет места, установить, нельзя ли применить способ группировки, ориентируясь на знаки слагаемых, их коэффициенты, их степени и разложение по степеням какого-либо множителя и т.п. 5. Выполнить выбранные преобразования, используя соответствующие приемы. 6. Записать ответ. 1 2 107 Доказательство тождеств 1. Изучить особенности выражения в каждой части равенства. 2. Установить, какое из следующих путей доказательства тождества удобно использовать для доказательства, упростить одну часть равенства (левую или правую), чтобы получить другую; упростить обе части равенства, чтобы получить равные выражения; доказать, что разность выражений, стоящих в разных частях данного равенства равна нулю. 3. Установить, какие из специальных преобразований нужно использовать для реализации выбранного в п. 2 пути доказательства. 4. Выполнить выбранные специальные преобразования, используя соответствующие правила, формулы и приемы по плану, выбранному в п.2. 5. Сделать вывод о равенстве двух выражений. 6. Сделать общий вывод о доказанности тождества. МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИЗУЧЕНИЯ ЛИНИИ УРАВНЕНИЙ И НЕРАВЕНСТВ Общая цель изучения: Овладение учащимися приемами решения уравнений и неравенств как математическим аппаратом решения разнообразных задач из математики, смежных областей знаний и практики. Распределение линии уравнений и неравенств по классам 108 Содержание материала Решение простейших уравнений на основе правил выполнения арифметических. Решение текстовых задач на составление уравнений. Линейное уравнение с одной переменной. Корень уравнения. Основные свойства уравнений. Решение текстовых задач с помощью линейных уравнений. Числовые неравенства и их свойства. Числовые промежутки. Действия над неравенствами. Линейное уравнение с двумя переменными. График линейного уравнения с двумя переменными. Система линейных уравнений. Аналитические способы решения системы линейных уравнений. Графический способ решения систем линейных уравнений. Решение текстовых задач составлением систем уравнений. Системы неравенств с двумя переменными и их решение. Квадратные уравнения и его корни. Неполные квадратные уравнения. Формула корней квадратного уравнения. Рациональные уравнения. Решение простейших систем уравнений второй степени с двумя переменными. Неравенства второй степени с одной переменной. Решение систем неравенств с одной переменной. Метод интервалов. Решение систем неравенств с двумя переменными. Решение простейших логарифмических и показательных уравнений и неравенств (только для классов с углубленным изучением математики). 109 Класс 5 класс 6 класс 6 класс 6 класс 8 класс 8 класс 9 класс Решение тригонометрических уравнений и неравенств. Решение систем тригонометрических уравнений и неравенств. Уравнения и неравенства с модулем. Уравнения и неравенства с параметрами (для профильных классов). Иррациональные уравнения и неравенства (для профильных классов). Показательные и логарифмические уравнения и неравенства. Системы показательных и логарифмических уравнений и неравенств. 10 класс 11 класс 11 класс 11 класс Учебные цели изучения линии уравнений и неравенств Категории целей Примеры обобщенных типов целей I уровень II уровень III уровень 1 2 3 4 110 Знание 1 Термины, обозначающие виды уравнений и процесс их решения, формулы и алгоритмы решения простейших уравнений, неравенств и их систем, их запись, частные приемы решения текстовых задач с помощью уравнений Определения видов уравнений и неравенств, формулировки их общих и различных свойств, общие методы и обобщенные приемы их решения и проверки, способы записи, общие приемы решения текстовых задач методом решения уравнений Обоснование методов и приемов решения уравнений, неравенств и их систем и совокупностей, общи, специальные и искусственные приемы их решения и решения задач методом решения уравнений 2 3 4 111 Понимание Умения и навыки Ученик правильно воспроизводит термины, формулы, алгоритмы и частные приемы решения простейших уравнений и неравенств, выполняет простейшие иллюстрации к задачам, приводит примеры Умения решать простейшие уравнения и неравенства по формулам, алгоритмам, частным приемам, по образцу или на основе помощи извне, проверять решение подстановкой Ученик интерпретирует методы и приемы решения уравнений, неравенств и систем, используя блоксхемы, графики, приводит контрпримеры, подводит уравнение, неравенство, задачную ситуацию под прием решения, выделяет главное в частных и специальных приемах их решения и проверки Умение решать типовые задачи в стандартных ситуациях, самостоятельно выбирать и использовать формулы, алгоритмы и приемы решения и проверки, составлять простейшие задачи 112 Ученик имеет представление об уравнениях и неравествах как моделях разнообразных задач, выделяет идеи обобщенных методов и приемов их решения и связи между ними, выводит следствия, перестраивает известные и находит новые приемы решения уравнений, неравенств и их систем и совокупностей, текстовых задач Умения решать уравнения и неравенства с параметрами, типовые и прикладные задачи методом уравнений и неравенств в нестандартных ситуациях, самостоятельно использовать обобщенные и искусственные приемы решения, проверки и переноса. Технологическая цепочка обучения решению уравнений Решение уравнений данного вида (по аналогии, с изученным ранее, «по соображению» и т.п.) Анализ действий необходимых для их решения. Вывод алгоритма (формулы, правила) решения и его отработка. Решение несложных уравнений данного вида не являющихся простейшими. Анализ действий, необходимых для их решения с применением алгоритмов (формул, правил). Формулировка частного приема решения. Применение полученного частного приема по образцу, в сходных ситуациях, в легко осознаваемых вариациях образца. Работа по выше описанным этапам для последующих видов уравнений. Сравнение полученных частных приемов решения, выделение общих действий в их составе и формулировка обобщенного приема решения уравнений нескольких видов. Применение обобщенного приема решения уравнений в различных ситуациях. Перенос и создание на его основе новых частных приемов для решения других видов уравнений Замечание: аналогическая цепочка строится для обучения решению неравенств с дополнительным использованием при этом сравнения с уравнениями. Вопрос о равносильности уравнений 113 Равносильность сохраняется 1. Если какой-нибудь член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение равносильное данному. (Обобщение первого свойства уравнений, 6 класс.) (1) f(x) = g(x) ⇔ (2) f(x)- g(x)=0 2. Если обе части уравнения возвести в нечетную степень, то получим уравнение, равносильное данному. f(x) = g(x) ⇔ (f(x))2b-1 = =(g(x))2b-1 3. af(x) = ag(x) ⇔ f(x) = g(x) (a > 0, a≠1) Появляется теоретически в 10-11 классах после изучения показательной функции, перед решением показательных уравнений. Равносильность может быть нарушена 1. Если обе части уравнения умножить на h(x), то f(x) = g(x) ? h(x)f(x) = h(x)g(x) ⇔ 2. Если обе части уравнения возвести в четную степень. f(x) = g(x) ? (f(x))2b = (g(x))2b ⇔ Специальные приемы решения задач по теме 114 Решение уравнения (неравенства, системы, совокупности) алгебраическим методом Поиск решения уравнения (неравенства, системы, совокупности) Тип задачи 1 1 Алгоритм выполнения приема 2 1. Определить по виду уравнения (неравенства, системы, совокупности) и прикидкой, каким методом можно воспользоваться. 2. Вспомнить известный (специальный или общий) прием использования этого метода и соотнести его с данным уравнением (неравенством, системой, совокупностью). 3. Определить возможные затруднения при использовании одного метода решения. 4. определить возможность и необходимость комбинации различных методов решения. 5. Разделить предполагаемый ход решения на части, соответствующие применению каждого метода, составить план решения каждой из них. 6. Составить общий план решения в целом. 1. Определить, является ли данное уравнение (неравенство, система, совокупность) простейшими какого-либо вида (если «да», то выполнить п. 5, если «нет» - п. 2). 2. Определить, если необходимо, ОДЗ уравнения (неравенства, системы, совокупности). 3. Установить, какие и в каком порядке необходимо выполнить тождественные и равносильные (общие или специальные для данного вида уравнений или неравенства) преобразований, чтобы привести данное уравнение (неравенство, систему, совокупность) к простейшим данного вида. 4. Выполнить выбранные преобразования, используя соответствующие приемы. 5. Решить известным способом (по формулу, алгоритму), полученные уравнение (неравенство, систему, совокупность). 6. Если необходимо сделать проверку и исследование. 7. Записать ответ, используя принятые приемы записи (в виде равенств, промежутков, их объединений или пересечений). 2 115 Специализация общего приема на основе конкретизации третьего этапа решения уравнений и неравенств алгебраическим методом На примере показательных уравнений и неравенств. 1. Определите, является ли это уравнение (неравенство) простейшим вида a f ( x ) = a g ( x ) ( a f ( x ) < a g ( x ) или a f ( x ) > a g ( x ) ): если «да», то п. 4, если «нет», - п. 2. 2. Установить, какие и в каком порядке нужно выполнить тождественные и равносильные преобразования (общие для всех уравнений или неравенств или специальные, основанные на свойствах степени или показательной функции), чтобы привести уравнение (неравенство) к простейшему. 3. С помощью выбранного преобразования привести уравнение (неравенство) к простейшему виду. 4. Заменить уравнение (неравенство) равносильным алгебраическим уравнением f ( x) = g ( x) (неравенством: при a > 1 f ( x) < g ( x) или f ( x) > g ( x) ; при 0 < a < 1 f ( x) > g ( x) или f ( x) < g ( x) ). 5. Решить полученное уравнение (неравенство), используя соответствующий прием. 6. Если нужно, сделать проверку и исследование. 7. Записать ответ. Замечание: Аналогичны приемы решения целых, дробно-рациональных, иррациональных, логарифмических и тригонометрических уравнений и неравенств. 1 2 116 Решение уравнения (неравенства) графическим методом 1. Определить, можно ли преобразовать какимлибо способом уравнение (неравенства) к виду f ( x) = g ( x) ( f ( x) > g ( x) ). 2. Если п. 1 имеет место выполнить преобразования, выбрав f (x) и g (x) наиболее простого вида. 3. Построить графики функций y = f (x) и y = g (x) в одной системе координат. 4. Найти абсциссы точек пересечения графиков, каждая из них – корень данного уравнения. 5. Найти промежутки на оси абсцисс, для которых график функции y = f (x) расположен выше графика функции y = g (x) , каждый из них есть решение данного неравенства. 6. Записать ответ. 1. Определить, можно ли каким-либо способом преобразовать неравенство к виду f ( x) > 0 или f ( x) < 0 . 2. Если п. 1 имеет место, выполнить преобразование, выбрав f (x) наиболее простого вида. 3. Найдите корни функции y = f (x) в области ее непрерывности и точки разрыва, если они существуют. 4. Отметить полученные значения на числовой оси. 5. Определить знак функции f (x) на каждом из полученных интервалов числовой оси (вычислением значения функции в удобной точке интервала или на основании теоремы о свойстве непрерывной функции). 6. Выбрать интервалы, на которых функция принимает нужное по знаку значение и записать ответ. 117 МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИЗУЧЕНИЯ ФУНКЦИОНАЛЬНОЙ ЛИНИИ Общая цель изучения: осознание учащимися понятия функции как одной из основных математических моделей, позволяющей описывать и изучать разнообразные зависимости между реальными величинами, и овладение методами исследование функций. Распределение функциональной линии по классам Содержание материала Класс Понятие о прямой и обратной 5 класс пропорциональности Прямоугольная система координат. Абсцисса и 6 класс ордината точки. Изображение точки по данным координатам. Примеры графиков движения, температуры, стоимости и др. Понятие о функции. Область определения и 6 класс область значений. Способы задания функции. Линейная функция ее график и свойства. Прямая пропорциональность, ее график и 7 класс свойства. Функция у=ах2, ее график и свойства. Функция у=ах3, ее график и свойства. Обратная пропорциональность. Функция у=k/x, ее 7 класс график и свойства. 8 класс Функция у= a , ее график и свойства. 2 Функция у=ах +bx+c, ее график и свойства. 8 класс Преобразование графиков. Свойства графиков: возрастание, убывание, четность, нечетность. Показательная, логарифмическая, степенная и 9 класс тригонометрические функции. Их свойства и график. Повторение ранее изученных функций их свойств 10 класс и графиков. Углубление изучения свойств функций: непрерывность периодичность, возрастание и убывание, экстремумы, ограниченность, сохранение знака. Преобразование графиков. Понятие об обратных функциях и их графиках. 118 Периодичность тригонометрических функций. Обратные тригонометрические функции. Понятие о пределе последовательности. Приращение функции. Предел функции в точке. Предел функции на бесконечности. Основные свойства предела. Непрерывность функции в точке и на промежутке. Свойства непрерывных функций. Производная и ее приложения. Степенная функция, ее свойства и график. Показательная и логарифмическая функции их свойства и графики. Первообразная и интеграл. 119 На основе исследования свойств функции с помощью производной Путем преобразования графика известной функции у=f(x) По характерным точкам, если общий вид графика известен По точкам, найденным из аналитического выражения функции Способы построения графиков функций 10 класс 10 класс 10 класс 11 класс 11 класс 11 класс Категории целей Учебные цели изучения функциональной линии Понимание Знание 1 Примеры обобщенных типов целей I уровень II уровень 2 Функциональная терминология, формулы и графики основных элементарных функций, приемы исследования с помощью графика, интуитивное понятие производной и интеграла функции, таблицы производных и первообразных функций III уровень 3 4 Определения Доказательства функциональных свойств функций, понятий и их дополнительные и свойств, частные обобщенные приеприемы исследо- мы исследования вания и способы функций, правила и записи свойств приемы дифференфункций, формулы цирования и Интеи правила диффе- грирования, различные области их приренцирования и ложений, методы и интегрирования, основные области обобщенные приеи их применения и мы решения прикладных задач, приечастные приемы решения приклад- мы переноса метоных задач дов Ученик правильно Ученик Ученик владеет воспроизводит интерпретирует представлением о термины, формулы, свойства функций функции как о важалгоритмы и методы их нейшей математирешения исследования при ческой модели, простейших любом способе переходит от одного функциональных языка описания к задания и при их задач, приводит другому, обосносравнении, примеры, вывает эквивалентприводит объясняет смысл ность формулироконтрпримеры, свойств функций и подводит вок на разных языих графическую ках, выделяет идеи задачную обобщенных метоинтерпретацию, ситуацию под дов и приемов геометрический и прием решения, механический выделяет главное исследования и связь между ними, смысл в частных и производной, перестраивает специальных первообразной и известные и приемах их интеграла находит новые решения и приемы функципроверки ональных и прикладных задач 120 Умения и навыки 1 2 Умения определять значение функции по значению аргумента, по формуле и по графику и решать обратную задачу, изображать графики основных элементарных функций, описывать свойства функций по графику, найти производные основных функций и вычислять простейшие интегралы, используя алгоритмы, по образцу или с помощью извне 3 Умения определять значение функции по значению аргумента и область определения функции при любом способе задания функции, исследовать свойства функций элементарными средствами, использовать свойства функций для сравнения и оценки их значений, решать типовые функциональные и прикладные задачи в стандартных ситуациях, самостоятельно выбирать и использовать формулы, алгоритмы, частные и специальные приемы решения, выражать в функциональной форме зависимости между величинами 121 4 Умения доказывать свойства функций, исследовать расположение графиков в координатной плоскости в зависимости от значений параметров, входящих в формулу, решать типовые функциональные и прикладные задачи в нестандартных ситуациях, самостоятельно использовать обобщенные приемы работы с функциями и их графиками, моделировать с помощью функций процессы и явления, составлять задачи Технологическая цепочка изучения свойств функций Мотивация введения новой функции (с помощью примеров и текстовых задач) 6-7 классы Подведение к понятию нового вида функции и введение ее определения в виде y=f(x), приведение примеров функций Выяснение области определения и области значений функции Построение графика функции по точкам в общем виде и в частных случаях, построения графика по характерным точкам Решение с помощью графика задач: отыскание значений функции по данному значению аргумента и обратно, отыскание промежутков знакопостоянства, возрастания и убывания, нулей функции Графическое решение соответствующего вида уравнений и неравенств 8-9 классы Отыскание промежутков монотонности функции на основе определения Решение простейших неравенств на основе монотонности функции Исследование на четность и нечетность по виду графика и на основе определения Отыскание наибольшего и наименьшего значения функции по графику и составлением и доказательством соответствующих неравенств 122 Исследование функции на периодичность на основе определения Отыскание нулей функции, через решение уравнения f(x)=0 Отыскание промежутков знакопостоянства функции через решение неравенств f(x)>0, f(x)<0 10-11 классы Исследование функции на дифференцируемость и отыскание производной, если она существует Исследование функции на монотонность с помощью производной Исследование функции на экстремумы с помощью производной и отыскание ее наибольших и наименьших значений Исследование функции на непрерывность на основе определения и свойств непрерывных функций Исследование функции на интегрируемость и отыскание первообразной, если она существует Установление существования обратной функции Обобщение и систематизация специальных тождественных преобразований, содержащих функцию, и приемов их использования при решении уравнений и неравенств 123 МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ВЕРОЯТНОСТНОСТАТИСТИЧЕСКОЙ ЛИНИИ В СРЕДНЕЙ ЩКОЛЕ Общая цель изучения: формирование у учащихся знаний о методах теории вероятностей и математической статистики как методах исследования и формах описания процессов окружающей действительности и овладение данными методами. Распределение вероятностно-статистической линии классам Содержание материала Класс Статистическая характеристика: мода. 6 класс Приближенное значение числа. Частота случайного события. Оценка вероятности 7 класс случайного события по частоте. Вероятностная шкала. Абсолютная и относительная погрешности. Статистическая характеристика: квадратичное 8 класс отклонение. Испытание. Событие – результат испытаний. 9 класс Действия над событиями. Вероятность события: статистическое, геометрическое определения. Обработка статистических данных: полигон, гистограмма, средняя выборка, размах квадратичного отклонения. Равномерное и нормальное распределение. Случайное событие. Классификация событий. 10 класс Вероятность события. Относительная частота события. Основные понятия комбинаторики. Операции над событиями. Теоремы сложения и умножения вероятностей. (Для профильных классов). Условная вероятность. Дискретная случайная 11 класс величина. Закон распределения случайной величины. Числовые характеристики дискретной случайной величины. Генеральная совокупность и выборка. Уровень значимости и достоверности. Понятие о законе простых чисел Учебные цели изучения вероятностно-статистической линии 124 Категории целей Понимание Знание 1 1 Примеры обобщенных типов целей I уровень II уровень 2 3 Вроятностностатистическая терминалогия, формулы и алгоритмы решения простейших задач по вычислению вероятности и основных статистических характеристик. Определения основных понятий теории вероятностей и статистики и их свойств, частные приемы их применения при решении прикладных задач. Ученик Ученик правильно интерпретируе воспроизводит т свойства термины, вероятности и формулы, статистически алгоритмы характеристики решения , подводит простейших задач задачную по теории ситуацию под вероятностей и прием математической решения, статистике, выделяет приводит главное в простейшие частных и примеры, специальных связанные с приемах их понятием решения и вероятности проверки случайного события и статистическими характеристикам и 2 3 125 III уровень 4 Простейшие доказательства свойств вероятности, дополнительные и обобщенные приемы решения прикладных задач, приемы переноса методов. Ученик владеет представлением о теории вероятностей и математической статистике как о методах исследования и формах описания объектов окружающей действительности , правильно интерпретирует теоремы о вероятностях, владеет обобщенными методами и приемами решения прикладных задач 4 Умения и навыки Умения находить частоту и вероятность случайного события, основные статистические характеристики представлять графически статистические данные. Умения находить вероятности исходов и событий, группировать статистические данные. 126 Умения использовать теоремы о вероятностях при решении прикладных задач, представлять в наиболее удобной форме и анализировать статистические данные. ГЕОМЕТРИЧЕСКАЯ ЛИНИЯ ШКОЛЬНОГО КУРСА МАТЕМАТИКИ Пропедевтический курс геометрии 5-6 классы 1. Окружность. Круг. Циркуль. Длина окружности. Площадь круга. Угол. Измерение углов. Построение угла заданной величины. Прямоугольный параллелепипед. Шар. Площади и объемы фигур. 2. Пересекающиеся прямые. Перпендикулярные прямые. Параллельные прямые. Прямоугольная система координат на плоскости. Осевая и центральная симметрия. Представление о подобии и равенстве фигур. Курс планиметрии 7-9 классы Курс стереометрии 9-11 классы 7 класс: Начальные поня-тия планиметрии. Углы и их виды. Параллельные прямые. Треугольники. Элементы треугольника. Виды треугольников. Признаки равенства треугольников. Построение треугольников по трем элементам. Окружность. Касательная к окружности. Хорды и углы в окружности. Описанная окружность. 8 класс: Четырехуголь-ники. Свойства и признаки четырехугольников. Теорема Фалеса. Соотношение между углами и сторонами в прямоугольном треугольнике. Площади фигур. 9 класс: Векторы на плоскости. Преобразование фигур на плоскости. Решение треугольников. Многоугольники. Правильные многоугольники. Вписанные и описанные многоугольники. Длина окружности. Площадь круга. 9 класс: Элементы стереометрии. Взаимное расположение прямых и плоскостей в пространстве. Представление о пространственных телах. 10 класс: Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей, перпендикулярность прямых и плоскостей. Векторы в пространстве. 11 класс: Многогранники. Элементы многогранников. Виды многогранников. Сечение многогранников. Правильные многогранники. Площади поверхностей многогранников. Тела вращения. Сечения тел вращений. Касательные плоскости. Площади поверхностей тел вращений. Объемы многогранников и тел вращения. Движения в пространстве. Векторы в пространстве. Уравнения линий и поверхностей в пространстве. 127 Цели изучения систематического курса геометрии Цели изучения пропедевтического курса геометрии Цели и задачи изучения геометрической линии школьного курса математики Категории Цели и задачи целей Основная цель: подготовить учащихся к изучению систематического курса геометрии. Задачи: 1. Развитие логического мышления учащихся, привитие элементарных навыков в определении простейших геометрических понятий, в формулировании выводов на основе наблюдений. 2. Формирование умений и навыков измерения геометрических величин. 3. Формирование умений и навыков в выполнении построений с помощью основных геометрических инструментов. Формирование рациональных приемов построения. 4. Развитие пространственных представлений учащихся. 5. Ознакомление учащихся с простейшими дедуктивными обоснованиями. 6. Развитие творческой активности и самостоятельности учащихся. Основная цель: систематическое изучение основных идей и фактов геометрии, методов их получения и обоснования и возможностей их применения. Задачи: 1. Ознакомление учащихся с ролью геометрии в формировании целостной научной картины мира. 2. Развитие у учащихся умений и навыков, обеспечивающих применение полученных знаний при решении геометрических задач, а также в смежных дисциплинах, в сфере производства и т.д. 3. Развитие у школьников геометрической интуиции и пространственного, конструктивного и логического мышления. 128 Функции школьного курса геометрии Культурноисторическая На примерах из истории развития геометрии прослеживается развитие многих ветвей математики, а также развитие человеческого общества и его культуры. Философская Геометрия помогает осмыслить мир, в котором мы живем, сформировать у человека развивающиеся научные представления о реальном физическом мире. Логическая Эстетическая Познавательная Прикладная Изучение геометрии является источником и эффективным средством активного интеллектуального развития человека, его умственных способностей. Воспитание эстетического вкуса на материале геометрии. Познание окружающего мира, его пространственных и количественных отношений. Элементарная геометрия является той базой, которая обеспечивает готовность человека к овладению другими дисциплинами, многими профессиями, делает доступным дальнейшее образование и самообразование. 129 Требования к геометрической подготовке учащихся средней школы Уровень Знания Умениям и навыки 1 2 3 -понятия об основных -распознавать и геометрических изображать основные 5-6 фигурах и телах; геометрические классы -понятие о величине фигуры; угла, длине, площади и -использовать необхообъеме, единицы димые инструменты измерения длин, для выполнения площадей и объемов и измерений; взаимосвязь между -использовать известними; ные формулы для -взаимное расположе- вычисления площадей ние прямых, понятие о и объемов простейпараллельных и ших геометрических перпендикулярных фигур и тел. прямых; -понятие об осевой и центральной симметриях. 7 класс - понятие об аксиомах и теоремах, обратных теоремах; - формулировки аксиом; - свойства смежных и вертикальных углов; - признаки равенства треугольников; - признаки параллельности и перпендикулярности прямых; - свойства внешних и внутренних углов треугольника; - свойства равнобедренного треугольника; - понятие об элементах окружности и их свойствах. 130 - использовать аксиомы и ранее изученные теоремы для доказательства теорем; - использовать метод рассуждения от противного для доказательства утверждений; - использовать признаки равенства треугольников при решении задач; -использовать при решении задач теоремы о свойствах фигур; - решать простейшие задачи на построение треугольников. 1 8 класс 2 - определения четырехугольника и его различных видов; -признаки и свойства различных видов четырехугольников; - теорема Пифагора и ей обратная теорема; - определение синуса, косинуса и тангенса острого угла прямоугольного треугольника; - соотношение между сторонами и углами в прямоугольном треугольнике; - неравенство треугольника; - формулы площадей треугольника и различных видов четырехугольников; - теорема Фалеса и свойства средних линий треугольника и трапеции; - замечательные точки треугольника и их свойства. 131 3 - распознавать виды четырехугольников; - выделять элементы четырехугольников в различных задачных ситуациях; - применять признаки и свойства различных видов четырехугольников для решения задач; - выводить формулы площадей треугольника и четырехугольников и применять их для вычисления площадей фигур; - применять теорему Фалеса при решении задач. 1 9 класс 2 - понятие вектора, координат вектора и его абсолютной величиины; - правила сложения, вычитания векторов, умножения вектора на число; - скалярное произведение векторов; - понятие о коллинеарности векторов; - понятие об основных преобразованиях плоскости и их свойствах; - определение подобных фигур, признаки подобия треугольников; - теоремы синусов и косинусов; - понятие о правильных многоугольниках, основные свойства правильных многоугольников; - формулы длины отрезка и координат середины отрезка; - уравнения прямой и окружности; - теорему о сумме углов выпуклого многоугольника; - формулы, выражающие радиусы вписанной и описанной окружностей через длину стороны правильного многоугольника; - понятие о расположении прямых и плоскостей в пространстве. 132 3 - выводить основные формулы в координатах; -применять векторнокоординатный метод для решения задач; - доказывать теоремы синусов и косинусов; - использовать теоремы синусов и косинусов для решения треугольников; - использовать преобразования плоскости для решения задач; - применять признаки подобия треугольников для решения задач; - вычислять элементы правильных многоугольников; - изображать случаи взаимного расположения прямых и плоскостей; - распознавать на моделях и в окружающих предметах основные пространственные тела. 1 10 класс 2 - основные понятия и аксиомы стереометрии; - определения параллельности прямых и плоскостей в пространстве, определение скрещивающихся прямых; - определения перпендикулярности прямых и плоскостей в пространстве, понятие угла межу скрещивающимися прямыми, между прямой и плоскостью двугранного угла между плоскостями; - признаки параллельности и перпендикулярности прямых и плоскостей в пространстве, теорема о трех перпендикулярах; - основные векторные формулы в пространстве. 133 3 - доказывать основные теоремы о параллельности и перпендикулярности в пространстве; - использовать признаки параллельности и перпендикулярности прямых и плоскостей в пространстве для решения задач; - использовать для решения задач основные векторные формулы в пространстве. 1 11 класс 2 - понятие об основных многогранниках, их видах и элементах; - понятие о правильном многограннике, виды правильных многогранников; понятие о теле вращения, виды тел вращения и их элементы; - понятие о касательной плоскости; формулы площадей поверхностей и объемов многогранников и тел вращения; - понятие об основных преобразованиях пространства и их свойствах; - понятие о коллинеарности и компланарности векторов в пространстве, о векторном базисе пространства; - уравнения линий и поверхностей в пространстве. 134 3 - изображать пространственные тела на плоскости; - устанавливать взаимное расположение линейных и угловых элементов многогранников и тел вращения и находить их величины; - строить сечения многогранников и тел вращения по заданным точкам или по расположению относительно элементов геометрического тела; - вычислять элементы построенных сечений; - выводить формулы площадей поверхностей и объемов многогранников и тел вращения и применять их при решении геометрических и практических задач; - использовать преобразования плоскости для решения задач; - выводить основные пространственные формулы в координатах; -применять векторнокоординатный метод для решения пространственных задач. ЛИТЕРАТУРА 1. Абылкасымова А.Е., Папышев А.А. Математические основы обучения решению задач в средней школе. – Алматы, 2004. – 124с. 2. Андреев В.И. Диалектика воспитания и самовоспитания творческой личности. Основы педагогики творчества. – Казань: Из-во Казанского у-та, 1988. – 236 с. 3. Арнольд В.И. Математика и математическое образование в современном мире // Математическое образование, − 1997. − № 2. − С. 109-112. 4. Бабанский Ю.К. Методы обучения в современной общеобразовательной школе. - М.: Просвещение, 1985 5. Бабанский Ю.К. Оптимизация учебно-воспитательного процесса. – М.: Просвещение, 1982. – 192 с. 6. Балл Г.А. Теория учебных задач: Психолого-педагогический аспект. – М.: Педагогика, 1990. – 184 с. 7. Беспалько Б.П. Слагаемые педагогической технологии. – М.: Педагогика, 1989. − 172 с. 8. Брунер Д. Психология познания / Пер. с англ., предисловие и общая редакция А.Р. Лурия. − М.: Прогресс, 1977. – 412 с. 9. Бурбаки Н. Архитектура математики //Математическое просвещение. – 1960. − № 5. – C. 245-259. 10. Бухарова Г.Д. Теоретико-методологические основы обучения решению задач студентов вуза: Автореф. дис. … д-ра пед наук. – Екатеринбург: Изд-во Уральского госпедуниверситета, 1996. − 38 с. 11.Выготский Л.С. Педагогическая психология. – М.: Педагогика, 1991. − 480 с. 12.Гальперин П.Я. Методы обучения и умственного развития ребенка. – М.: Изд-во МГУ, 1995. – 208 с. 13.Ганеев Х.Ж. Теоретические основы развивающего обучения математике. − Екатеринбург: УрГПУ, 1997 − 160 с. 135 14. Гельфман Э.Г., Холодная Н.А. Психологический аспект исследования задач на уроках математики // Роль и место задач в формировании системы основных знаний. Сб. науч. Работ. – М.: Изд-во НИИ школ МП РСФСР, 1976. – С. 22-34. 15.Гин А.А. Приемы педагогической техники: свобода выбора. Пособие для учителя. – М.: Вита-Пресс, 1999 16.Глейзер Г.И. История математики в школе. - М.: Просвещение, 1981 - 1983. 17.Гнеденко Б.В. Математика и математическое образование в современном мире. – М.: Просещение, 1985. − 191с. 18.Государственные образовательные стандарты среднего общего образования Республики Казахстан. – Алматы: РОНД, 2002. – 368 с. 19.Груденов Я.И. Совершенствование методики работы учителя математики: кн. для учителя. – М.: Просвещение, 1990. – 224 с. 20.Гусев В.А. Психолого-педагогические основы обучения математике. − М.: ООО «Издательство «Вербум-М», ООО «Издательский центр «Академия», 2003. – 432 с. 21.Давыдов В.В. Виды обобщения в обучении / 2-е изд. – М.: Педагогическое общество России, 2000. – 480 с. 22. Далингер В.А. Задачи в обучении математике: Методические рекомендации для студентов физико-математических факультетов педагогических институтов и учителей математики средних школ. – Омск: Изд-во Омского пединститута, 1990. − 43 с. 23.Данилов М.А., Есипов Б.П. Дидактика / Под общ. ред. Б.П. Есипова. – М.: Изд-во АПН РСФСР, 1967. – 518 с. 24.Джонсон Д. и др. Методы обучения. Обучение в сотрудничестве / пер. с англ. З.С. Замчук. – СПб.: Экономическая школа, 2001 25.Дьюи Дж. Психология и педагогика мышления. – М.: Лабиринт, 1999. – 192 с. 26. Епишева О.Б. Технология обучения математике на основе деятельностного подхода. – М.: Просвещение, 2003. – 223 с. 136 27.Епишева О.Б., Крупич В.И. Учить школьников учиться математике: Формирование приемов учебной деятельности: Кн. для учителя. − М.: Просвещение, 1990. − 128 с. 28.Загвязинский В.И. Теория обучения: Современная интерпритация: Учеб. пособие для студ. высш. пед. учеб. заведений. – М.: «Академия», 2001. – 192 с. 29.Занков Л.В. Избранные педагогические труды. Дидактика и жизнь. Обучение и развитие. − М.: Педагогика, 1990. – 424 с. 30. Зинченко П.И. Непроизвольное запоминание. Институт практической психологии. – Москва-Воронеж, 1996. – 544 с. 31. Зотов Ю.Б. Организация современного урока. – М.: 1984. – 144 с. 32.Калошина И.П. Психология творческой деятельности: Учебное пособие для втузов. − М.: ЮНИТИ-ДАНА, 2003. – 41с. 33.Кириллова Г.Д. Теория и практика урока в условиях развивающего обучеия. – М.: Просвещение, 1980. – 159 с. 34.Колмогоров А.Н. Математика – наука и профессия. – М.: Педагогика, 1990. − 142 с. 35.Колягин Ю.М. Задачи в обучении математике: Часть Ι: Математические задачи как средство обучения и развития учащихся. – М.: Просвещение, 1977. − 110 с. 36.Колягин Ю.М. Задачи в обучении математике: Часть ΙΙ: Обучение математике через задачи и обучение решению задач. – М.: Просвещение, 1977. − 144 с. 37.Колягин Ю.М., Оганесян В.А. и др. Методика преподавания математики в средней школе. Общая методика. – М.: Просвещение, 1975. 38.Колягин Ю.М., Оганесян В.А. и др. Методика преподавания математики в средней школе. Частная методика. – М.: Просвещение, 1977. 39.Конаржевский Ю.А. Анализ урока. – М.: Центр «Педагогический поиск», 2000. – 336 с. 40.Крупич В.И. Структура и логика процесса обучения математике в средней школе: Методические разработки по 137 спецкурсу для слушателей ФПК. – М.: Изд-во МГПИ, 1985. − 117 с. 41.Крутецкий В.А. Психология математических способностей школьников. – М.: Просвещения, 1968. − 481с. 42.Лернер И.Я. Дидактические основы методов обучения. – М.: Педагогика, 1981. −185 с. 43.Лоповок Л.М. 1000 проблемных задач по математике. − М.: Просвещение, 1995. − 239 с. 44.Лурия А. Р. Маленькая книжка о большой памяти. − М.: Эйдос, 1994. – 96 с. 45. Манвелов С.Г. Конструирование современного урока математики. ̶ М.: Просвещение, - 175 с. 46.Матюшкин А.М. Проблемные ситуации в мышлении и обучении. – М.: Педагогика, 1985. – 208 с. 47.Махмутов М.И. Организация проблемного обучения в школе. – М.: Просвещение, 1977. – 240 с. 48.Методы обучения в современной школе: Сб. статей / Под ред. Н.И.Кудряшева. – М.: Просвещение, 1983 49.Оконь В. Основы проблемного обучения. – М.: Просвещение, 1968. − 208 с. 50.Осинская В.Н. Формирование умственной культуры учащихся в процессе обучения математике. – Киев, 1989. – 192 с. 51.Пидкасистый П.И. Самостоятельная познавательная деятельность школьников в обучении: Теоретикоэкспериментальное исследование. – М., 1980. – 240 с. 52.Пойа Д. Математическое открытие. Решение задач: основные понятия изучение и преподавание. – М.: Наука, 1970. – 452 с. 53.Пуанкаре А. Математическое творчество. – СПб., 1909. − 155 с. 54.Рубинштейн С.Л. Проблемы общей психологии. – М.: Педагогика, 1976. − 416 с. 55.Саранцев Г.И. Методика обучения математике в средней школе. − М.: Просвещение, 2002. − 224 с. 138 56.Саранцев Г.И. Метод обучения как категория методики преподавания // Педагогика. – 1998. - №1.- С. 28 57. Саранцев Г.И. Теоретические основы методики упражнений по математике в средней школе: Автореф. дисс. … доктора пед. наук.- Л.: Изд-во Ленинградского педуниверситета, 1987. – 36 с. 58.Саранцев Г.И. Упражнения в обучении математике, т.4. – М.: Просвещение, 1995. – 240 с. 59.Скаткин М.Н. Совершенствование процесса обучения. – М., 1971. − 129 с. 60.Слепкань З.И. Психолого-педагогические основы обучения математике: Метод. пособие. – Киев.: Рад. Школа, 1983. − 192с. 61.Столяр А.А. Педагогика математики: Учеб. пособие для физ.мат. фак. пед. ин-тов. – Минск, 1986. − 381с. 62.Тихомиров О.К. Психология мышления: Учеб. пособие для студ. выс. учеб. заведений. − М.: Изд. Центр «Академия», 2002. − 288 с. 63.Фридман Л.М. Логико-психологический анализ школьных учебных задач. − М.: Педагогика, 1977. − 203 с. 64.Фридман Л.М., Кулагина И.Ю. Психологический справочник учителя. − М.: Просвещение, 1991. − 288 с. 65.Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Пособие для учащихся. -2-е изд., перераб. и доп. – М.: Просвещение, 1984. – 175 с. 66.Хуторской А.В. Практикум по дидактике и современным методикам обучения. – СПб.: Питер, 2004 – 541 с. 67.Шмигирилова И.Б. Организация обобщающего повторения планиметрии на основе поисковых заданий: учебнометодическое пособие. – Петропавловск, 2005. – 160 с. 68.Эльконин Д.Б. Психология и педагогика памяти. – Киев, 1948. − 64 с. 69.Эсаулов А.Ф. Психология решения задач. – Минск: Вышейшая школа, 1977. – 216 с. 139 70.Якиманская И.С. Развивающее обучение. − М.: Педагогика, 1979. – 144 с. ОГЛАВЛЕНИЕ 140 ПРЕДИСЛОВИЕ…………………………………………………2 РАЗДЕЛ 1. ОБЩАЯ МЕТОДИКА……………………………..4 Предмет теории и методики обучения математики……………..4 Структура теории и методики обучения математике……………5 Уровни целеполагания…………………………………………….6 Общие цели обучения математике ..….…………………………..6 Функции обучения математике…………………………………...7 Задачи обучения математике……………………………………...8 Составные части и характеристики процесса обучения…………8 Принципы обучения………………………………………………12 Методы обучения математике……………………………………14 Формы обучения ...………………………………………………..21 Средства обучения математики..……………………………… 21 Контроль и оценка знаний……………………………………….22 Урок – основная форма обучения………………………………..26 Уровневый анализ учебно-познавательной деятельности учащихся ………………………………………………………….52 Математические понятия. Методика работы над определением …………………………………………….………54 Теорема. Виды теорем. Методика работы над теоремой………60 Задачи в обучении математике…………………………………..66 РАЗДЕЛ 2. ЧАСТНАЯ МЕТОДИКА………………………….91 Основные содержательно-методические линии школьного курса математики…………………………………………………91 Методические особенности изучения числовых множеств и действий над числами…………………………………………….91 Методические особенности изучения линии тождественных преобразований выражений……………………………………..95 Методические особенности изучения линии уравнений и неравенств………………………………………………………..100 Методические особенности изучения функциональной линии……………………………………………………………..109 141 Методические особенности изучения вероятностностатистической линии в средней школе………………………..115 Геометрическая линия школьного курса математики………...118 ЛИТЕРАТУРА………………………………………………….126 142

Теория и методика обучения математике в понятиях, схемах и таблицах, Шмигирилова И.Б., 2007

Related documents

Products

Support

Теория и методика обучения математике в понятиях, схемах и таблицах, Шмигирилова И.Б., 2007

Related documents

Add this document to collection(s)

Add this document to saved

Suggest us how to improve StudyLib