курсовая Одноэтажное промышленное здание

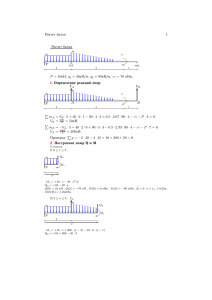
Министерство образования Республики Беларусь
Белорусская государственная политехническая академия
Кафедра „ Железобетонные и каменные конструкции "
РАСЧ Е Т Н О - П ОЯ С Н И Т ЕЛ Ь Н А Я З А П И С К А
к курсовому проекту
на тему: "Одноэтажное каркасное промышленное здание
"
по дисциплине: "Железобетонные и каменные конструкции "
Исполнитель:
студент гр. 111222
Иванов И.И.
Руководитель:
Иванов И.И.
Минск 2001 г
Ра
СОДЕРЖАНИЕ
Введение. .............................................................................................................................. 3
1.1. Задание на проектирование ..................................................................................... 5
1.2. Определение генеральных размеров поперечной рамы цеха. .............................. 6
2. Установление нагрузок на поперечную раму цеха. .................................................. 7
2.1. Нагрузка от собственного веса конструкции покрытия ....................................... 7
2.2. Снеговая нагрузка..................................................................................................... 9
2.3. Ветровая нагрузка ................................................................................................... 10
2.4. Крановая нагрузка .................................................................................................. 12
3. Статический расчёт рамы. ......................................................................................... 14
4. Расчет стропильной двускатной балки..................................................................... 14
4.1. Задание на проектирование. .................................................................................. 14
4.2. Предварительное назначение размеров балки ..................................................... 14
4.3. Определение площади рабочей арматуры. .......................................................... 15
4.4. Определение потерь ............................................................................................... 17
4.5. Расчёт прочности наклонных сечений по поперечной силе. ............................. 19
4.6. Расчёт по образованию трещин нормальных к оси балки. ................................. 22
Расчёт конька балки........................................................................................................... 24
4.7. Расчёт балки на трещиностойкость при транспортировке и монтаже. ............. 25
4.8. Расчёт балки по образованию трещин, наклонных к продольной оси элемента.30
5. Расчёт и конструирование колонны крайнего ряда. ............................................... 33
5.1. Исходные данные: .................................................................................................. 33
5.2. Расчёт надкрановой части колонны. ..................................................................... 33
5.3. Расчёт подкрановой части колонны. .................................................................... 38
6. Расчёт внецентренно нагруженного фундамета под крайнюю двухветвевую
колонну. ............................................................................................................................... 42
6.1. Конструктивное решение. Основные геометрические размеры. ....................... 42
6.2. Определение нагрузок и усилий, действующих на основание и фундамент ... 43
6.3. Определение размеров подошвы фундамента. .................................................... 44
6.4. Расчёт тела фундамента. ........................................................................................ 45
Литература .......................................................................................................................... 53
ВВЕДЕНИЕ.
В разрабатываемом курсовом проекте рассчитывается железобетонный каркас одноэтажного производственного здания согласно основным принципам расчета, конструирования и компоновки железобетонных конструкций.
Сбор нагрузок осуществляется в соответствии со СНиП 2.01.07-85 'Нагрузки и воздействия', а расчет конструкций — в соответствии со СНиП 2.03.0184* 'Бетонные и железобетонные конструкции. Нормы проектирования'.
Сравнительно большие пролеты современных промышленных зданий наиболее
экономично перекрывать ж/б балками, так как ж/б фермы получатся очень трудоёмкими и
более сложными в монтаже.
Для уменьшения нагрузок вместо применявшихся долгое время и продолжающих
применяться сейчас тяжелых железобетонных плит покрытия в проекте применяется легкое покрытие из лёгкого ж/б с использованием эффективного утеплителя.
Применявшиеся ранее железобетонные подкрановые балки были очень недолговечны и быстро выходили из строя вследствие плохого восприятия динамической нагрузки.
Сейчас они полностью вытеснены стальными подкрановыми балками.
Под предельным понимается такое состояние конструкции, после достижения которого ее дальнейшая нормальная эксплуатация становится невозможной вследствие потери способности сопротивляться внешним нагрузкам и воздействиям или получения недопустимых перемещений и местных повреждений. Железобетонные конструкции должны удовлетворять требованиям расчета по несущей способности — предельные состояния
первой группы и по пригодности к нормальной эксплуатации — предельные состояния
второй группы.
Расчет по предельным состояниям первой группы должен обеспечит необходимую
прочность и устойчивость конструкции, чтобы предотвратить:
 хрупкое, вязкое или иного характера разрушение;
 потерю устойчивости формы конструкции (расчет на устойчивость тонкостенных конструкций т.п.) или ее положение (расчет конструкции на опрокидывание, скольжение, всплытие и т.д.);
 усталостное разрушение (расчет на выносливость конструкций, находящихся
под действием многократно повторяющейся нагрузки — подвижной или пульсирующей: подкрановых балок, шпал, рамных фундаментов и перекрытий под
неуравновешенные машины и т. п.);
 разрушение от совместного действия силовых факторов и неблагоприятных
влияний внешней среды (агрессивная среда, попеременное замораживание и оттаивание и т. п.).
Расчет по предельным состояниям второй группы выполняют, чтобы предотвратить:
 образование в конструкциях трещин и их чрезмерное или длительное раскрытие
(если по условиям эксплуатации образование или длительное раскрытие трещин недопустимо);
 чрезмерное перемещения (прогибы, углы поворота и перекоса, колебания).
Расчет по предельным состояниям конструкций в целом, а также отдельных ее
элементов производится для всех стадий: изготовления, транспортирования, возведения и
эксплуатации, причем расчетные схемы должны соответствовать принятым конструктивным решениям. При расчете по предельным состояниям учитывают следующие факторы:
 нагрузки и воздействия, их вероятные отклонения (в основном превышение) от
средних значений, неблагоприятное сочетание нагрузок постоянных и временных (длительных, кратковременных и особых);
 механические характеристики бетона и арматуры (временное сопротивление,
предел текучести), изменчивость этих характеристик, условия работы материалов;
 общие условия работы конструкций, условия ее изготовления, агрессивность
среды и т.п.
В расчетных формулах отклонения нагрузок учитываются коэффициентом надежности по нагрузке f, изменчивость механических характеристик материалов — коэффициентами надежности по бетону b и арматуре s, условия работы — коэффициентами bi, si,
степень ответственности зданий и сооружений — коэффициентами надежности по назначению конструкций n = 0.8  1. На коэффициент n умножаются расчетные нагрузки или
усилия либо делятся расчетные сопротивления материалов или несущая способность элемента.
Таким образом, расчетом по предельным состояниям гарантируется, что за расчетный период эксплуатации сооружения не наступит ни одно из недопустимых предельных
состояний для конструкции в целом и для отдельных ее частей.
1.1.
ЗАДАНИЕ НА ПРОЕКТИРОВАНИЕ
Запроектировать в сборном железобетоне одноэтажное промышленное здание по
исходным данным.
Исходные данные
Таблица 1.1
Схема поперечной рамы здания
Пролет, м
22
Шаг колонны, м
9
Количество шагов колонны
16
Высота до оголовка подкранового рель-
12
са, м
Грузоподъемность крана, тс
Несущая стропильная конструкция
16
Двускатная балка
Сопротивление грунта, МПа
0.24
Район строительства
Казань
Напрягаемая арматура
AIIIв
Утеплитель
z = 12 см
 = 300 кг/м3
Требуется:
1. На основании эскизного проектирования выбрать основной вариант конструктивного решения здания.
2. Произвести статический расчет поперечной рамы цеха.
3. Рассчитать железобетонные конструкции:
— предварительно напряженную стропильную конструкцию;
— колонну крайнего ряда;
— фундамент под колонну.
1.2.
ОПРЕДЕЛЕНИЕ ГЕНЕРАЛЬНЫХ РАЗМЕРОВ
ПОПЕРЕЧНОЙ РАМЫ ЦЕХА.
Компоновку поперечной рамы начинают с установления основных габаритных размеров элементов конструкций в плоскости рамы. Вертикальные габариты здания зависят
от технологических условий производства и определяются расстоянием от уровня пола до
головки кранового рельса и расстоянием от головки кранового рельса до низа конструкций
покрытия.
Высота от уровня рельса до низа стропильных ферм h2  hк 100+f, кратна 200 мм
h2  2300  100 + 250  2650 мм
Принимаем h2=2700 мм
Размер верхней части колонны — Нв  h2+ hб , где
hбвысота подкрановой балки (принимаем 1200 мм)
Нв  2700+1200  3900 мм
Высота цеха от уровня пола до низа балки
H= h1 +h2=12000+2700=14700
Высота нижней части колонны — Нн  H – Нв + 0,15  14.7-3,9+0,15  10.95 м
Привязку нижней грани колонны к разбивочной оси принимаем 250 мм
Высота сечения верхней части колонны назначаем h2 = 600 мм.
Высота сечения нижней части колонны h1 зависит от принятой привязки грани колонны к разбивочной оси и от привязки кранового рельса и равна их сумме. Высота сечения нижней части колонны будет равна h2  1200 мм.
1 
1 
 1
 1
Ширина сечения колонны равна b    h2    1200  600  480
 20 25 
 20 25 
Принимаем b=500 мм
Рис. 1. Генеральные размеры поперечной рамы цеха.
2. УСТАНОВЛЕНИЕ НАГРУЗОК НА ПОПЕРЕЧНУЮ РАМУ ЦЕХА.
На поперечную раму цеха действуют постоянные нагрузки от веса ограждающих и
несущих конструкций здания, временные от мостовых кранов и атмосферные воздействия
снега ветра.
На здание может действовать одновременно несколько нагрузок и возможно несколько комбинаций их с учетом отсутствия некоторых из них или возможного изменения
схем их приложения. Поэтому раму рассчитывают на каждую из нагрузок отдельно, а затем составляют расчетную комбинацию усилий при невыгодном сочетании нагрузок. При
этом значения нагрузок должны подсчитываться отдельно, если даже они имеют одинаковые схемы распределения на конструкции, но отличаются по длительности воздействия.
2.1.
НАГРУЗКА ОТ СОБСТВЕННОГО ВЕСА КОНСТРУКЦИИ ПОКРЫТИЯ
Постоянные нагрузки на ригель рамы от веса кровли, стропильных ферм и связей по
покрытию принимаются обычно равномерно распределенными по длине ригеля.
Постоянные нагрузки зависят от типа покрытия, которое может быть тяжелым или
легким, утепленным или не утепленным. В данном курсовом проекте применяется тип покрытия ж/б плиты.
Покрытие состоит из ж/б плит, опирающихся непосредственно на балки, пароизоляции, теплоизоляционного слоя водоизоляционного ковра, защитного слоя. защитным.
Нагрузка от покрытия определяется суммированием отдельных элементов его значения,
которых сведены в таблицу:
Нормативные и расчетные нагрузки на 1 м2 покрытия
Табл.1.2
№
1
2
3
4
5
6
7
8
Наименование нагрузки
Нормативная Н/м2
I Постоянная
Бранирующий слой из гравия
втопленного в битумную
мастику 300 кг/м3
Гидроизоляционный ковер из 3х слоев рубероида на битумной
мастике 200 кг/м3
Цементно-песчаная стяжка,
= 3 см = 2000 кг/м3
Утеплитель минераловатный
= 12 см = 300 кг/м3
Пароизоляция из одного слоя
рубероида = 50 кг/м3
Выравнивающий слой из цементного р-ра =20 мм
=2000 кг/м3
Сборная ж/б ребристая плита,
= 70 мм = 2500 кг/м3
Собственная масса балки
ИТОГО
9
ВСЕГО
f
n
Расчетная,
Н/м2
300
1.3
0.95
370,5
200
1,2
0,95
228
600
1,3
0,95
741
360
1,1
0,95
376,2
50
1,2
0,95
57
400
1,3
0,95
494
1750
1,1
0,95
1828,75
631,31
1,1
0,95
659,72
4291,31
II Временная
Снеговая нагрузка г. Казань
1500
5791,31
Расчетная нагрузка на погонный метр балки:
qмрасч  g∙B  6550,17·9  58,95 кН/м.
Нормативная нагрузка на погонный метр балки:
qмn  gn∙B  5791,31·9  52,12 кН/м.
4755,17
1,4
0,95
1795
6550,17
2.2.
СНЕГОВАЯ НАГРУЗКА
Расчетная погонная снеговая нагрузка на балку определяется по формуле:
s  sо∙μ∙B∙γn∙γf ,
где so — нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли, принимаемая в зависимости от района строительства. Город Казань
расположен в IV–ом снеговом районе. Нормативное значение снеговой нагрузки
so  1.5 кПа;
μ — коэффициент, учитывающий конфигурацию покрытия; для расчета рамы принимается μ = 1;
γf — коэффициент надежности по нагрузке, для снега принимаемый в зависимости от
отношения нормативной нагрузки от веса покрытия к нормативному значению
веса снегового покрытия. Отношение gn/so = 5,79/1.5 = 3.86 > 0.8, следовательно,
γf = 1.4;
B — шаг стропильных конструкций.
Определим расчетную погонную снеговую нагрузку на балку:
s  sо∙μ∙B∙γn∙γf = 1.5∙1∙9∙0.95∙1.4 = 17.955 кН/м;
Определим нормативную погонную снеговую нагрузку на балку:
sn  sо∙μ∙B= 1.5∙1∙9= 13.5 кН/м.
ВЕТРОВАЯ НАГРУЗКА
2.3.
Расчет поперечных рам здания выполняется только на статическую составляющую
ветровой нагрузки ,соответствующей установившемуся напору на здание. Характер распределения статической составляющей ветровой нагрузки определяется по формулам:
с наветренной стороны (напор)
wm = wokcγnγf ,
где
wo — нормативное значение ветрового давления, принимаемое в зависимости от района строительства. Город Казань расположен в II–ом ветровом районе, wo  0.30 кПа;
k — коэффициент, учитывающий изменение ветрового давления в зависимости от высоты здания
с — аэродинамический коэффициент; c  0.8  для наветренной стороны,
c  0.6  для подветренной стороны.
Погонная ветровая нагрузка на колонну равна:
qw = wokcγf B = 0.30k0.8(0.6)1.4 9, кН/м
т.к k  меняется в зависимости от высоты, то и qw будет также изменяться в зависимости
от высоты. Для упрощения расчёта фактическую ветровую нагрузку заменяем эквивалентной, равномерно распределенной по высоте колонны. Величину эквивалентной
нагрузки находим из условия равенства изгибающих моментов в защемлённой стойке от
фактической эпюры ветрового давления и от равномерно распределённой нагрузки. Ветровую нагрузку на шатёр (от низа до верха балки), заменяем сосредоточенной силой W,
приложенной в уровне низа балки:
qнаветр. 0.31.40.890.300.75  2.268 кН/м;
qнаветр. 0.31.40.890.301.0  3.024 кН/м;
qнаветр. 0.31.40.890.301.1175  3.38 кН/м;
W=0.5(3.38+3.52) 1.8=6.21 кН
W’=W0.6/0.8=4.66 кН
M
qв (hв  hн ) 2
2M
2  321.61
 qв 

 2.92 кН / м
2
2
(hв  hн )
(3.9  10.95) 2
qв' 
qв'  0.6 0.6  2.92

 2.19 кН / м
0.8
0.8
2

M  5  2.268  2.65  5  2.268  7.65  0.5  5  0.756    5  5.15   4.7  3.024  12.5 
3

2

 0.5  4.7  0.356    5  10.15   321.61 кН  м
3

Рис. Схема нагрузок на крайнюю колонну.
КРАНОВАЯ НАГРУЗКА
2.4.
Производственные здания часто оборудуются большим числом мостовых кранов в
каждом пролете. Одновременная работа всех кранов в режиме их максимальной грузоподъемности, отвечающая наиболее неблагоприятному воздействию на поперечную раму,
маловероятна. Поэтому при расчете однопролетных рам крановую нагрузку учитывают
только от двух кранов наибольшей грузоподъемности с учетом коэффициента сочетаний.
Вертикальная крановая нагрузка передается на подкрановые балки в виде сосредоточенных сил Fmax и Fmin при их невыгодном положении на подкрановой балке. Расчетное давление на колонну, к которой приближена тележка, определяется по формуле:
Dmax = γn∙γf∙ψ∙∑Fmax∙yi;
на противоположную колонну:
Dmin = γn∙γf∙ψ∙∑Fmin∙yi,
где
γf = 1.1 — коэффициент надежности по нагрузке для крановых нагрузок;
ψ = 0.85 — коэффициент сочетаний при совместной работе двух кранов для
групп режимов работы кранов 1К–6К;
Fmax — наибольшее вертикальное давление колес на подкрановую балку;
Принимаем следующие характеристики для крана
Q = 16т: Fmax = 185 кН, база крана А = 4400 мм, ширина крана В = 6300 мм, масса тележки
53 кН, масса крана 310 кН.
B
A
Fmax
Fmax
Fmax
0.300
0.789
1
Fmax
0.511
Рис. 3. .
Минимальное давление колес крана можно определить по формуле
Fmin = (Q  G)/n0  Fmax,
где
Q — грузоподъемность крана в т;
G — полный вес крана с тележкой;
n0 — число колес на одной стороне крана.
Fmin = ( 310  160 ) / 2  185 = 50 кН.
Dmax = 0.951.10.851852.60 = 427.25 кН;
Dmin = 0.951.10.85502.60 = 115.47 кН.
При торможении тележки крана на колонны рамы действует горизонтальная поперечная нагрузка. Нормативная горизонтальная поперечная сила Тоn  действующая вдоль
моста крана, при гибком подвесе определяется по формуле
Тоn = 0.05(Q + Gт)/n0,
где
Gт — вес тележки.
Тоn = 0.05(160 + 53)/2=5.325 кН.
Расчетное горизонтальное давление на колонну от двух сближенных кранов равно:
Т = γn∙γf ∙ψ∙Ткn∙∑ yi = 0.95∙1.1∙0.85∙5.325∙2.60 = 12.30 кН.
3. СТАТИЧЕСКИЙ РАСЧЁТ РАМЫ.
Статический расчёт рамы выполняется на основании собранных выше нагрузок и
по определённым ранее размерам поперечной рамы цеха. Статический расчёт необходим
нам для дальнейшего расчёта колонны и фундамента.
Расчет производим на комплексе ЛИРА, с использованием программы подготовки
файла исходных данных kp2.
Результаты расчета приведены в приложении 1.
4. РАСЧЕТ СТРОПИЛЬНОЙ ДВУСКАТНОЙ БАЛКИ.
4.1.
ЗАДАНИЕ НА ПРОЕКТИРОВАНИЕ.
Рассчитать и законструировать предварительно-напряжённую двускатную балку для
покрытия промышленного здания. Расстояние между разбивочными осями здания L  22
м; шаг балок В  9 м. Балка изготавливается из бетона В40 с тепловой обработкой; армирование  напрягаемая арматура AIIIв, натягиваемая механическим способом. Конструктивная арматура из стали класса АIII.
Расчетные данные.
Принимаем класс бетона B40:
Eb  36000 МПа
Rb  22 МПа
Rb ,ser  29 МПа
Rbt  1.4 МПа
Rbt , ser  2.10 МПа
Принимаем арматуру AIIIв:
Es  180000 МПа
Rs ,ser  540 МПа
Rs  490 МПа
Принимаем арматуру AIII:
Es  200000 МПа
Rs ,ser  390 МПа
Rsw  390 МПа
Rs  365 МПа
Rsc  200 МПа
 sp  Rs ,ser  540 МПа
Rsc  365 МПа
4.2.
Rsw  290 МПа
ПРЕДВАРИТЕЛЬНОЕ НАЗНАЧЕНИЕ РАЗМЕРОВ БАЛКИ
В общем случае размеры сечений балок назначаются из следующих соображений:
высота сечения по средине балки h  1 / 10…1 / 15 L; уклон верхнего пояса 1 / 12; ширина
верхней сжатой полки bf'  1 / 50…1 / 60 L (обычно 300500 мм); ширина нижнего пояса
300400 мм с учётом удобства размещения всей напрягаемой арматуры; толщина стенки b
 60…120 мм; уклоны скосов полок 3045о; высота сечения на опоре типовых балок 790
мм. Приняты следующие размеры сечения балки: b 'f  40 см , h'f  20,5 см , b f  30 см ,
h f  21см
ОПРЕДЕЛЕНИЕ ПЛОЩАДИ РАБОЧЕЙ АРМАТУРЫ.
4.3.
Высота балки в коньке равна 170 см.
Определим расчётный пролёт l0  2200  2.5  2  2  0.5  (60  25  2.5)  2162.5 см
Определим наиболее опасное сечение
x  0.37lo  0.37  21.625  8.0 м
Момент в наиболее опасном сечении равен
qx
58.95  8.0
M
(lo  x) 
 (21.625  8.0)  3212.86 кН  м
2
2
Граничная высота сжатой зоны бетона равна:

0.6916
R 

 0.718 , где
 SR
 50
0.6916

(1 
)
1
(1  ) 1 
500
1.1

1.1
  0.85  0.008  Rb   b 2  0.85  0.008  22  0.9  0.6916
Высота балки в опасном сечении
1
h  79  (800  16,25  2,5)  147 см
12
Для арматуры класса АIIIв  SR  RS   SP  490  540  50 МПа
Определяем положение нейтральной оси
М П  Rb b2 b 'f h 'f h0  0,5h 'f  Rsc As' z s
h0 = h - a = 114 - 9 = 138 см
zs = h0 - a' = 138 - 8 = 130 см
М П  22  100 0,9  40  20,5  138  0,5  20,5  365  100 6.16 130  2366.44 кН  м
М П  2344.66 кН  м  М x  3212.86 кН  м — при таком соотношении н.о. проходит в
ребре. Имеем второй случай расчета тавровых сечений.




h'
M  (b 'f  b)h 'f Rb (h0  f )  As Rsc z s 
2


Определяем  m 
2
bh0 Rb b 2
20.5
)  365  100  6.16 130]
2
m 
 0.316
22  100  0,9 10 1382
По  m =0.316 находим   0,393 и   0.803
 R  0.393    0.718 — сечение непереармировано. Можем продолжать расчет.
bh0 Rb b 2  (b 'f  b)h 'f Rb b 2  As Rsc
Asp 

Rsp s 6
3212.86 105  [( 40  10)  20.5  22 100  (138 
10  0.393 138  22 100  0.9  (40  10)  20.5  22 100  0.9  6.16  365 100
 45.05 см 2
490 100 1.14
где  s 6 — коэффициент, который учитывает работу стали за пределами условного предела
текучести, определяется по формуле
 

 0.393 
 1  1.14    1,15
 s 6      1 2  1  ,  s 6  1,15  1,15  1 2
 0.718 
 R 
где  — коэффициент, принимаемый равным 1,15 для арматуры класса AIIIв
Принимаем  s 6  1.14
Для обеспечения трещиностойкости преднапряженной железобетонной балки площадь рабочей арматуры увеличим на 10% Аsp  45.05  4.505  49.56 см2
Окончательно принимаем 16Ø20 AIIIв с Аsp = 50.29 см2
Определение геометрических характеристик сечения
Для арматуры класса AIII α = Es / Eb = 200000 / 36000 = 5,56
Для арматуры класса A-IIIв α = Es / Eb = 180000 / 36000 = 5,0
Определяем площадь приведенного сечения
Ared  bi hi  40  20.5  21 30  10  (147  21  20.5)  5  50.29  5.56  6.16  2790.70 см 2
Определяем статический момент железобетонной балки относительно оси, проходящей по линии грани сечения
20.5 

S red  bi hi yi  40  20.5  147 
  5.56  6.16  147  8  10  147  20.5  21 
2 

21
 147  20.5  21


 21  30  21   5  50.29  9  203579.99 см 3
2
2


Определяем расстояние от нижней грани до центра тяжести приведенного сечения
S
203579.99
y0'  147  72.95  74.05 cм
y0  red 
 72.95 см
Ared
2790.70
Определяем момент инерции приведенного сечения

40  20.53
20.5 

2
I red  I i  Ai y 
 40  20.5   74.05 
  5.56  6.16  (74.05  8) 
12
2


2
2
i
30  213
21 
(147  20.5  21)3 10

 30  21  72.95    5  50.29  (72.95  9) 2 

12
2
12

2

 (147  20.5  21) 10  (73.75  72.95) 2  8003589.58 см 4
Определение упругого момента сопротивления балки
I
8003589.58
 109713.36 см 3
а) для нижней растянутой грани сечения Wred  red 
y0
72.95
I
8003589.58
 108083.59 см 3
б) для верхней сжатой грани сечения W red'  red' 
y0
74.05
4.4. ОПРЕДЕЛЕНИЕ ПОТЕРЬ
Определение потерь предварительного напряжения арматуры в балке при механическом способе натяжения. Натяжение на упоры.
I. Первые потери
1. Потери от релаксации напряжений проволочной арматуры
 1  0.1 sp  20  0.1  540  20  34 МПа
2. Потери от температурного перепада
2  1,25t  1,25  65  81,25МПа
где Δt — разность между температурой нагреваемой арматуры и неподвижных упоров (вне
зоны нагрева) , воспринимающих усилие натяжения, ºС.
3. Потери от деформации анкеров, расположенных у натяжных устройств
l
4.25
 3  Es 
180000  33.33МПа
l
22950
где Δl — смещение стержней в инвентарных зажимах, определяемое по формуле
l  1,25  0,15d  1,25  0,15  20  4.25 мм
d — диаметр стержня, мм
l — длина натягиваемого стержня, мм
Определение коэффициента точности натяжения
Значение предварительного натяжения в арматуре вводится с коэффициентом точности
натяжения арматуры γsp, определяемым по формуле
 sp  1   sp  1  0,1  0,9.
Знак «плюс» принимается при неблагоприятном влиянии предварительного натяжения, знак «минус» — при благоприятном.
Значения Δγsp при механическом способе натяжения арматуры принимаются равными 0,1.
Определение суммарных первичных потерь
 los1   1   2   3  34  81.25  33.33  148.58МПа
Определение усилия обжатия балки преднапряженной арматурой
P1   sp Asp  sp   los1   0.9  50.29  540  148.58  100  1771.61Кн
Определение эксцентриситета действия силы P1
eop  y0  a  72.95  9  63.95 см
Определение расчётно-изгибающего момента в середине балки от собственной массы в период ее распалубки
q  l 2 5.7  21.6252
М с .в .  с .в . 0 
 333.19 кН  м
8
8
Нормативный момент
М
333.19
М сn.в.  с.в. 
 273.11кН  м
 fсс
1.22
Определяем напряжения в бетоне балки на уровне центра тяжести сечения от действия собственной массы балки и усилия обжатия Р1
 bp 
3
3
5
P1  eop  M с.в.
P1
 y0  a   1771.6110  1771.6110  63.95  273.1110

Ared
I red
2790.70
8003589.58
 72.95  9  13.22 МПа
Rbp = (0,7–0,8)B = 0,8 · 40 = 32 МПа
 bp 13.22

 0.41
Rbp
32
Определяем расстояние до верхней и нижней ядровых точек
rяв   n
Wred 109713.36

 39.31см
Ared
2790.70
 n  1,6 
 bp
Rbp
rян   n
'
Wred
108083.59

 38.73 см
Ared
2790.70
 1.6  0.41  1.19 1
bp — напряжение в железобетонной балке на уровне центра тяжести сечения
Rbp — передаточная прочность бетона
Определяем упругопластический момент сопротивления для верхней и нижней граней сечения
'
W pl  Wred
Wpl'  Wred
γ — зависит от формы и размеров сечения и принимается равным 1,5
Wpl  1.5 109713.36  164570.34 см3
Wpl'  1.5 108083.59  162125.39 см3
4. Определение от быстронатекающей ползучести

 bp
 6  40 bp 0,85  40  0.41 0085  13.94 МПа

при
Rbp
Rbp
где α — коэффициент принимаемый по формуле
  0,25  0,025Rbp  0,25  0,025  32  1.05  0.8
 bp
 0.41    0.8
Rbp
0,85 — коэффициент, учитывающий термообработку.
Определяем полные первые потери
 los1   1   2   3   6  148.58  13.94  162.52МПа
II. Вторые потери
1. Потери от усадки бетона
По табл.5 СниП 2.03.01-84 «Бетонные и железобетонные конструкции» принимаем
 8  40МПа
2. Потери от ползучести бетона

 bp
 9  150 bp  150  0.85  0.41  52.28МПа
 0,75
при
Rbp
Rbp
α — коэффициент, учитывающий тепловую обработку бетона, принимаемый равным
0,85.
Определение вторых потерь
 los2   8   9  40  52.28  92.28МПа
Определяем суммарные потери
 los   los1   los2  162.52  92.28  254.80МПа
Величина обжатия балки с учетом полных потерь
P2   sp Asp  sp   los   0.9  50.29  540  254.80  100  1290.84 Кн
4.5.
РАСЧЁТ ПРОЧНОСТИ НАКЛОННЫХ СЕЧЕНИЙ ПО ПОПЕРЕЧНОЙ СИЛЕ.
В сечении х1:
Поперечная сила равна Q  q(l0 / 2  x1 )  58.95  (
21.625
 0.4375)  611.61 кН
2
Размеры балки в сечении 1-1 (х1=437.5 мм):
h  h оп  i  (a  x1  25)  79 
(170  79)
(16.25  43.75  2.5)  84.2 см
1100
h o  h  a sp  84.2  9  75.2 см
b  10 см
Коэффициент f , учитывающий влияние свесов сжатой полки:
f  0.75(b'f  b)h'f / (bh0)  0.75(400  100)205 / (100*752)  0.61>0.5.
В дальнейшем принимаем f 0.5
Влияние продольного усилия обжатия N  P2  1290.84 кН.
n 
0.1 N
0.11290.84 103

 1.36  0.5,
Rbt  b  h0   b 2 1.4 100  0.9 10  75.2
следовательно, принимаем f 0.5 n  0.5.
Параметр 1 + f + n 1 + 0.5 + 0.5  2> 1.5, следовательно, принимаем 1.5.
В расчетном сечении
Q b   b 2 1   f   n R bt bh 02 / c b , но менее  b3 1   n R bt bh 0 .
Q b  2 1.5 1.4 100 10  75.2 2 / 75.2  315.84 кН >
0.6 1.5 1.4 100 10  75.2  94.752 кН
На приопорном участке принимаем хомуты из трёх ветвей  10 мм из арматуры
класса A–III с шагом S  150 мм, что удовлетворяет условию:
 S  150 < h / 3  842 / 3  281 мм.
Усилие, воспринимаемое хомутами у опоры на единицу длины балки:
qsw  RswAsw / S  290100 2,36 /15  4562,67 Н/см.
Длина проекции опасной наклонной трещины:
c0 
 b 2  1   f   n  Rbt   b 2  b  h02
qsw

2 1.5 1.4 100 10  0.9  75.22
 68.45 см  h 0  75.2 см.
4562.67
Принимаем с0 = 752 мм. Поперечное усилие Qsw = qswс0 = 456,30.752 = 312.31 кН.
Поперечная сила, воспринимаемая хомутами и бетоном в наклонном сечении с
длинной проекции опасной наклонной трещины с0  752 мм:
Qb,sw = Qb + Qsw = 315,84 + 312.31 = 628,15 кН > Q  611.61 кН,
т.е. прочность сечения на действие поперечной силы Q обеспечена.
В сечении х2:
Поперечная сила равна Q  q(l0 / 2  x1 )  58.95  (
21.625
 4.325)  382.44 кН
2
Размеры балки в сечении 2-2 (х2=4325 мм):
h  h оп  i  (a  x 2  25)  79 
(170  79)
(16.25  432.5  2.5)  116.33 см
1100
h o  h  a sp  116.33  9  107.33 см
b  10 см
Коэффициент f , учитывающий влияние свесов сжатой полки:
f  0.75(b'f  b)h'f / (bh0)  0.75(400  100)205 / (100*1073,3)  0.43<0.5.
В дальнейшем принимаем f 0.43
Влияние продольного усилия обжатия N  P2  1290.84 кН.
n 
0.1 N
0.11290.84 103

 0.95  0.5,
Rbt  b  h0   b 2 1.4 100  0.9 10 107.33
следовательно, принимаем f 0.43 n  0.5.
Параметр 1 + f + n 1 + 0.43 + 0.5  1.93> 1.5, следовательно, принимаем 1.5.
В расчетном сечении
Q b   b 2 1   f   n R bt bh 02 / c b , но менее  b3 1   n R bt bh 0 .
Q b  2 1.5 1.4 100 10 107.332 / 138.15  350.22 кН >
0.6 1.5 1.4 100 10 107.33  135.24 кН
На втором участке принимаем хомуты из трёх ветвей  10 мм из арматуры класса
A–III с шагом S  300 мм, что удовлетворяет условию:
 S  150 < h / 3  1163,3 / 3  388 мм.
Усилие, воспринимаемое хомутами у опоры на единицу длины балки:
qsw  RswAsw / S  290100 2,36 /30  2281,33 Н/см.
Длина проекции опасной наклонной трещины:
c0 
 b 2  1   f   n  Rbt   b 2  b  h02
qsw

2 1.5 1.4 100 10  0.9 107.332
 138.15 см  h 0  107.33 см.
2281.33
Принимаем с0 = 1381,5 мм. Поперечное усилие Qsw = qswс0 = 228,11,38 = 315,17 кН.
Поперечная сила, воспринимаемая хомутами и бетоном в наклонном сечении с
длинной проекции опасной наклонной трещины с0  1381,5 мм:
Qb,sw = Qb + Qsw = 350,22 + 315,17 = 665,39 кН > Q  382.44 кН,
т.е. прочность сечения на действие поперечной силы Q обеспечена.
В сечении х3:
Поперечная сила равна Q  q(l0 / 2  x3 )  58.95  (
21.625
 8.65)  127.50 кН
2
Размеры балки в сечении 3-3 (х3=8650 мм):
h  h оп  i  (a  x1  25)  79 
(170  79)
(16.25  865  2.5)  152.11 см
1100
h o  h  a sp  152.11  9  143.11 см
b  10 см
Коэффициент f , учитывающий влияние свесов сжатой полки:
f  0.75(b'f  b)h'f / (bh0)  0.75(400  100)205 / (100*1431,1)  0.32<0.5.
В дальнейшем принимаем f 0.32
Влияние продольного усилия обжатия N  P2  1290.84 кН.
n 
0.1 N
0.11290.84 103

 0.72  0.5,
Rbt  b  h0   b 2 1.4 100  0.9 10 143.11
следовательно, принимаем f 0.32 n  0.5.
Параметр 1 + f + n 1 + 0.32 + 0.5  1.82> 1.5, следовательно, принимаем 1.5.
В расчетном сечении
Q b   b 2 1   f   n R bt bh 02 / c b , но менее  b3 1   n R bt bh 0 .
Q b  2 1.5 1.4 100 10 143.112 / 2 143.11  300.53 кН >
0.6 1.5 1.4 100 10 143.11  180.32 кН
На третьем участке из конструктивных соображений принимаем хомуты из трёх
ветвей  10 мм из арматуры класса A–III с шагом S  300 мм, что удовлетворяет условию:
 S  150 < h / 3  1521.1 / 3  507 мм.
РАСЧЁТ ПО ОБРАЗОВАНИЮ ТРЕЩИН НОРМАЛЬНЫХ К ОСИ БАЛКИ.
4.6.
Расчёт по образованию трещин производится из условия: M r  M crc
где:
Мr — момент внешних сил
Mcrc — момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин и определяемый по формуле
M crc  R bt ,ser Wpl  M rp ,
Момент сил обжатия относительно верхней ядровой точки:
M rp  P(eop  rяв )  1290.84 103  (63.95  39.31)  1332.92 кН  м
Момент, воспринимаемый сечением балки в стадии эксплуатации непосредственно перед
образованием трещин
M crc  2.1100 164570.34  1332.92 105  1678.52 кН  м <
M
3445.93
n
Мr= M max
 max 
 2824.53 кН  м  элемент работает с трещинами.
 f ,ср
1.22
Ширину раскрытия трещин, нормальных к продольной оси элемента, acrc, следует
определять по формуле: acrc= acrc,1- acrc,2+ acrc,3

где a crc ,i  l s 20(3.5  100  )3 d
Es
 — коэффициент равный 1.0
 — коэффициент, принимаемый равным для стержневой арматуры периодического
профиля 1.0
l — коэффициент, принимаемый равным при учёте:
кратковременных нагрузок и непродолжительного действия постоянных и длительных нагрузок 1,0
продолжительного действия постоянных и длительных нагрузок для конструкций из
тяжёлого бетона 0,8
 s — приращение напряжений от действия внешней нагрузки, определяемое по
M n max  Pz
формуле  s 
A sp z
 h 'f
2
 h f   

z  h 0 1  0
2( f   ) 





  1.8 — для тяжёлого бетона


1
1.5   f

 1.0
1  5(   )
es,tot

11.5
5
10
h0
n
M max
2824.53 105

 0.51
bh02 Rb , ser 10 1382  29 100
f 
(b 'f  b)h 'f 
bh0
h
'
f
 '
5.56
As (40  10)  20.5 
 6.16
2
2

0
.
45

0.47
10 138
20.5
)  0.44
2h0
2 138
es ,tot — эксцентриситет силы P относительно центра тяжести площади сечения арматуры S
   f (1 
)  0.47  (1 
M 2824.53

 2.19 м
P 1290.84
es ,tot / h0  2.19 / 1.38  1.59  1.2 /  ls  1.2 / 1.1  1.09
es ,tot 
 ls  1.1 — коэффициент, принимаемый равным для стержневой арматуры периодического профиля при нагрузке непродолжительного действия.
 ls  1.6  15 — при нагрузке продолжительного действия
Asp
50.29


 0.049  0.02
'
'
bh0  (b f  b)( h f  asp ) 10 138  (40  10)  (20.5  9)
В дальнейшем принимаем   0.02
1
1.5  0.47


 0.28  1.0
1  5(0.51  0.44)
219
1.8 
11.5 
5
10  0.002  5
138
 20.5
2
 138  0.47  0.28 
z  138  1 
  124.36 см
2

(
0
.
47

0
.
28
)




5
2824.53 10  1290.84 103 124.36
s 
 194.94 МПа
50.29 124.36
194.94
a crc,1  1.0  1.0  1.0 
 20  (3.5  100  0.02)  3 20  0.088 мм — ширина раскрытия
180000
трещин от непродолжительного действия полной нормативной нагрузки.
Определим ширину раскрытия трещин от непродолжительного действия длительной
нагрузки, т.е. a crc, 2
1.5  9  21.6252
n
M ln  M max
 M shn  2824.53  (
)  2035.39 кН  м
8
Mn
2035.39 105
 2 l

 0.37
bh0 Rb , ser 10 1382  29 100
M 2035.39

 1.58 м
P 1290.84
es ,tot / h0  1.58 / 1.38  1.14  1.2 /  ls  1.2 / 1.1  1.09
es ,tot 
В дальнейшем принимаем es ,tot / h0  1.14
1
1.5  0.47

 0.39  1.0
1  5(0.37  0.44) 11.5 1.14  5
1.8 
10  0.002  5
 20.5
2
 138  0.47  0.39 
z  138  1 
  120.19 см
2

(
0
.
47

0
.
39
)




5
2035.39 10  1290.84 103 120.19
s 
 80.06 МПа
50.29 120.19
80.06
acrc, 2  1.0 1.0 1.0 
 20  (3.5  100  0.02)  3 20  0.036 мм
180000
Определим ширина раскрытия трещин от длительного действия длительной нагрузки, т.е. a crc ,3

es ,tot / h0  1.58 / 1.38  1.14  1.2 /  ls  1.2 / 0.8  1.5
В дальнейшем принимаем e s , tot / h 0  1.5
l  1.6 15  0.02  1.3
 '
5.56
(b 'f  b)h 'f 
As (40  10)  20.5 
 6.16
2

2

0
.
15
 

 0.53
f
10 138
bh0
h
'
f
20.5
)  0.49
2h0
2 138
1
1.5  0.53


 0.31  1.0
1  5(0.37  0.49) 11.5 1.5  5
1.8 
10  0.002  5
 20.5
2
 138  0.53  0.31 
z  138  1 
  123.64 см
2  (0.53  0.31) 



5
2035.39 10  1290.84 103 123.64
s 
 70.67 МПа
50.29 123.64
70.67
acrc,3  1.0 1.3 1.0 
 20  (3.5  100  0.02)  3 20  0.042 мм
180000
Ширину раскрытия трещин, нормальных к продольной оси элемента равна
acrc= acrc,1- acrc,2+ acrc,3=0.088-0.036+0.042=0.094 мм <0.3 мм
   f (1 
)  0.53  (1 
РАСЧЁТ КОНЬКА БАЛКИ
Усилие действующее в коньке
2М
Д
tg
ho  0.5h 'f
ql 02 58.95  21.625 2

 3445.93 кНм
8
8
h0  h  a  170  9  161 см
1
tg 
12
2  3445.93 105 1
Д
  380.98 кН
161  0.5  20.5 12
Определим требуемую площадь арматуры, которая будет удерживать верхний пояс от
отрыва
Д 380.98 103
As 

 10.44 см 2
Rs
365 100
Принимаем 6 16AШ (As = 12.06 cм2).
где М 
4.7.
РАСЧЁТ БАЛКИ НА ТРЕЩИНОСТОЙКОСТЬ ПРИ ТРАНСПОРТИРОВКЕ И
МОНТАЖЕ.
в
Отрицательный момент, действующий на балку M  M кон
св  (e op  rя )
Определим геометрические характеристики в сечении а-а:
(170  79)
 150  91.4 см
Высота сечения h  79 
1100
Рабочая высота сечения h 0  h  a sp  91.4  9  82.4 см
Отношение модулей упругости
s 
E s 180000

 5.0
Eb
36000
s 
E s' 200000

 5.56
Eb
36000
Площадь приведенного сечения балки:
Ared  40  20.5  21 30  (91.4  20.5  21) 10  5  50.29  5.56  6.16  2234.70 см 2
Статический момент сечения относительно нижней грани:
S red  40  20.5  (91.4 
 30  21
20.5
 91.4  20.5  21

)  (91.4  20.5  21) 10  
 21 
2
2


21
 5.56  6.16  (91.4  8)  5  50.29  9  101206.52 см 3
2
Расстояние от центра тяжести приведенного сечения до нижней грани:
у0 
S red 101206.52

 45.29 см
Ared
2234.70
Расстояние от центра тяжести приведенного сечения до верхней грани:
у0'  h  y0  91.4  45.29  46.11см
Момент инерции приведенного сечения относительно центра тяжести сечения:
40  20.53
20.5 

2
I red  I i  Ai y 
 40  20.5   46.11 
  5.56  6.16  (46.11  8) 
12
2 

2
2
i
30  213
21 
(91.4  20.5  21)3 10


 30  21  45.29    5  50.29  (45.29  9) 2 

12
2
12

2
 (91.4  20.5  21) 10  (45.95  45.29) 2  2353510.91см 4
Момент сопротивления приведенного сечения:
Wred 
I red 2353510.91

 51965.35 см 3
y0
45.29
I red 2353510.91

 51041.23 см 3
'
y0
46.11
W ' red 
Эксцентриситет усилия предварительного обжатия относительно центра тяжести
приведенного сечения: eop  y0  asp  45.29  9  36.29 см
Сжимающие напряжения в бетоне в стадии предварительного обжатия:
bp 
bp
Rbp
P1eop  M свн
P1
1771.61103 1771.61103  273.11105

eop 

 36.29  13.63 МПа
Ared
I red
2234.70
2353510.91

13.63
 0.43
32
n  1.6 
bp
Rbp
 1.6  0.43  1.17 1.0  принимаем  n  1.0
Расстояние от центра тяжести приведенного сечения до верхней ядровой точки:
rяв  n
Wred
51965.35
 1.0 
 23.25 см
Ared
2234.70
Расстояние от центра тяжести приведенного сечения до нижней ядровой точки:
rян  n
W ' red
51041.23
 1.0 
 22.84 см
Ared
2234.70
Момент сопротивления приведенного сечения относительно центра тяжести сечения
для нижней растянутой грани с учётом неупругих деформаций бетона:
Wpl  Wred  1.5  51965.35  77948.03 см3
Момент сопротивления приведенного сечения относительно центра тяжести сечения
для верхней сжатой грани с учётом неупругих деформаций бетона:
W ' pl  W ' red  1.5  51041.23  76561.85 см3
Момент образования трещин равен M crc  Rbt ,serWpl'  2.1100  76561.85  160.78 кН  м
Действующий момент в сечении равен
M  M свкон  P1 (eop  rяв ) 
5.7  (1.5  0.025) 2
 1771.61 (0.3629  0.2325)  237.22 кН  м
2
M  237.22 кН  м  M crc  160.78 кН  м  элемент работает с трещинами и ширину
раскрытия трещин, нормальных к продольной оси элемента увеличиваем на 10 % т.е.
acrc = 0.094 + 0,0094 = 0.1 мм < 0.3 мм
Определение кривизны железобетонных элементов на участках с трещинами в растянутой зоне должна определяться по формуле:
1 1 1 1 1
       
r  r 1  r  2  r  3  r  4
1
  — кривизна от непродолжительного действия всей нагрузки, на которую про r 1
изводится расчет по деформациям.
1
  — кривизна от непродолжительного действия постоянных и длительных
 r 2
нагрузок.
1
  — кривизна от продолжительного действия постоянных и длительных нагру r 3
зок.
1
  — кривизна, обусловленная выгибом элемента вследствие усадки и ползуче r 4
сти бетона от усилия предварительного обжатия и определяемая по формуле:
 1 b  b
  
h0
 r 4
'
1 1
1
Кривизна   ,   и   определяется по формуле:
 r 1  r  2  r  4
 N tot  s
b
1 M  s

,
 


 r  h 0 z  E s A sp ( f   )bh 0 E b  h 0 E s A sp
1
1
при этом   и   вычисляются при значениях  s и , отвечающих непродол r 1  r  2
1
жительному действию нагрузки, а   – при  s и , отвечающих продолжительному дей r 3
ствию нагрузки.
Коэффициент  s для элементов из тяжелого бетона определяется по формуле:
 s  1.25   ls m 
1   m2
, но не более 1,0
(3.5  1.8 m )es , tot / h 0
 ls — коэффициент, учитывающий влияния длительности действия нагрузки.
m 
R bt ,ser Wpl
M r  M rp
< 1.0
1
Определим кривизну от непродолжительного действия всей нагрузки —  
 r 1
 ls  1.1
 b  0.9
m 
Rbt , serW pl
M r  M rp

2.10 100 164570.34
 0.08  1.0
2824.53 105  1332.92 105
 s  1.25  1.1 0.08 
1  0.082
(3.5  1.8  0.08) 1.38
 0.86
5

0.86
0.9
 1  2824.53 10 

  


6
5
 r 1 138 124.36 18 10  50.29 (0.47  0.28) 10 138  36 10  0.45 

1290.84 103
0.86

 8.75 10 6 см 1
138
18 106  50.29
Определим кривизну от непродолжительного действия постоянных и длительных
1
нагрузок —  
 r 2
M = 2035.39 кН м
m 
Rbt , serW pl
M r  M rp

2.10 100 164570.34
 0.10  1.0
2035.39 105  1332.92 105
 s  1.25  1.1 0.10 
1  0.10 2
(3.5  1.8  0.10) 1.09
 0.87

2035.39 105 
0.87
0.9
1

  


6
5
 r  2 138 120.19 18 10  50.29 (0.47  0.39) 10 138  36 10  0.45 

1290.84 103
0.87

 8.55 10 6 см 1
6
138
18 10  50.29
Определим кривизну от продолжительного действия постоянных и длительных
1
нагрузок —  
 r 3
M = 2035.39 кНм
 f  0.53
Z=123,64 см
  0.15
  0.31
 s  1.25  0.8  0.10 
1  0.102
(3.5  1.8  0.10) 1.5
 0.97

2035.39 105 
0.97
0.9
1

  


6
5
 r 3 138 123.64 18 10  50.29 (0.53  0.31) 10 138  36 10  0.15 

1290.84 103
0.97

 1.26 10 5 см 1
138
18 106  50.29
Определим кривизну, обусловленную выгибом элемента вследствие усадки и ползу-
1
чести бетона от усилия предварительного обжатия —  
 r 4
b

 b'
 1   b   b Es Es

  
h0
h0
 r 4
'
b  6  8  9  13.94  40  52.28  106.22 МПа
 b'  0
 1  106.22 100
 4.28 106 см 1
  
6
 r  4 18 10 138
Полная кривизна равна:
1 1 1 1 1
             (8.75  8.55  12.60  4.28) 106  8.52 106 см 1
r  r 1  r  2  r 3  r 4
Определим прогиб балки по формуле f  f1  f 2  f 3  f 4
где:
f1 
1 1 2 1
6
2
  l0   8.75 10  2162.5  4.09 см
10  r 1
10
f2 
5 1 2 5
6
2
  l0   8.55 10  2162.5  4.16 см
48  r  2
48
11
1
f 3    l02  12.60 106  2162.52  7.35 см
8  r 3
8
11
1
f 4    l02   4.28 106  2162.52  2.50 см
8  r 8
8
Прогиб балки равен:
f  f1  f 2  f 3  f 4  4.09  4.16  7.35  2.50  4.78 см 
няется.
1
l0  8.65 см  условие выпол250
4.8.
РАСЧЁТ БАЛКИ ПО ОБРАЗОВАНИЮ ТРЕЩИН, НАКЛОННЫХ К
ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА.
Расчёт по образованию трещин, наклонных к продольной оси элемента, должен производится из условия
 mt   b 4 R bt,ser
где  b 4 — коэффициент условий работы бетона, определяемый по формуле
1   mt / R b,ser
, но не более 1,0
 b4 
0.2  B
здесь  — коэффициент, принимаемый равным для тяжёлого бетона 0,01
В — класс бетона по прочности на сжатие.
Значения главных растягивающих и главных сжимающих напряжений в бетоне определяются по формуле
x  y 
   xy2
 mc ( mt )  
 
2
2


— нормальное напряжение в бетоне на площадке, перпендикулярной проx
дольной оси элемента, от внешней нагрузки и усилия предварительного обжатия.
P
x  2
A red
A red — площадь приведенного сечения.
В сечении II-II (х=437,5 мм):
Q = 611.61 кН
h = 84.2 см
 x   y
2
Ared  40  20.5  21  30  (84.2  20.5  21)  10  5  50.29  5.56  6.16  2162.70 см 2
P2 1290.84 103

 596.87 Н / см 2  5.97 МПа
Ared
2162.7
 y — нормальное напряжение в бетоне на площадке, параллельной продольной оси
элемента, от местного действия опорных реакций, сосредоточенных сил и распределенной
нагрузки, а также усилия обжатия вследствие предварительного напряжения хомутов и
отогнутых стержней.
y  0
x 
 xy — касательное напряжение в бетоне от внешней нагрузки и усилия обжатия
вследствие предварительного напряжения отогнутых стержней.
QS
 xy  red ,1
I red b
Статический момент сечения относительно нижней грани:
20.5
 84.2  20.5  21

S red  40  20.5  (84.2 
)  (84.2  20.5  21) 10  
 21 
2
2


21
 30  21  5.56  6.16  (84.2  8)  5  50.29  9  90210.32 см 3
2
Расстояние от центра тяжести приведенного сечения до нижней грани:
у0 
S red 90210.32

 41.71 см
Ared
2162.7
Расстояние от центра тяжести приведенного сечения до верхней грани:
у0'  h  y0  84.2  41.71  42.49 см
Момент инерции приведенного сечения относительно центра тяжести сечения:
40  20.53
20.5 

2
I red  I i  Ai y 
 40  20.5 42.49 
  5.56  6.16  (42.49  8) 
12
2


2
2
i
30  213
21 
(84.2  20.5  21)3 10

 30  21  41.71    5  50.29  (41.71  9) 2 

12
2
12

2

 (84.2  20.5  21) 10  (42.35  41.71) 2  1892685.44 см 4
21.5 

S red1  40  20.5   42.49 
  5.56  6.16  (42.49  8) 
2 

 42.49  20.5 
3
 (42.49  20.5) 10  
  30035.87 см
2


3
611.6110  30035.87
 xy 
 9.71 МПа
1892685.44 10

5.97
 
 5.97 
2
 mc   x   x    2xy  
 
  9.71  13.14 МПа  Rb , ser  29 МПа
2
2
2
2


 
2
2

5.97
 
 5.97 
2
 mt   x   x    2xy  
 
  9.71  7.17 МПа
2
2
2
2


 
Расчёт по образованию трещин, наклонных к продольной оси элемента, должен производится из условия
 mt   b 4 R bt,ser
2
1  mt / Rb,ser
2
1  13.14 / 29
 0.96 1.0
0.2  B
0.2  0.01 40
 mt  7.17 МПа   b 4 Rbt , ser  0.96  2.10  2.016 МПа  элемент работает с трещинами.
Ширина раскрытия трещин, наклонных к продольной оси элемента, при армировании хомутами, нормальными к продольной оси, должна определяться по формуле:
b4 

0.6 sw d w
dw
Es
 0.15E b (1  2w )
h0
A
2.36
 w  sw 
 0.016
bs 10 15
Q  Qb
(611.61  315.84) 103
 sw 
S
15  249.99 МПа
Aswh0
2.36  75.2
0.6  249.99 100 1 1.15
acrc  1.5 
 0.028 см  0.03 см
1
7
5
2 10 
 0.15  36 10  (1  2  5.56  0.016)
75.2
Длина зоны передачи усилий определяется по формуле:
  sp

lp   p
 p d 15d
 p  0.25 p  10
 R

bp


540


l p   0.25 
 10   20  285 мм 15d  300 мм
32


Принимаем длину зоны передачи усилий равной l p  300 мм
a crc   l
5. РАСЧЁТ И КОНСТРУИРОВАНИЕ КОЛОННЫ КРАЙНЕГО РЯДА.
5.1.
ИСХОДНЫЕ ДАННЫЕ:
Бетон тяжелый класса В 30, подвергнутый тепловой обработке при атмосферном
давлении Rb = 17 МПа; Eb = 29 10 3 МПа, Rbt = 1.2 МПа.
В расчетное сопротивление бетона Rb следует ввести коэффициент условий работы
бетона b2:
 при учете постоянных, длительных и кратковременных нагрузок, кроме крановых и ветровых, b2 = 0.9;
 при учете постоянных, длительных и кратковременных нагрузок, включая крановые и ветровые нагрузки, b2: =1.1.
Продольная арматура класса AIII, Rs = 365 МПа, Rsc = 365 МПа, Еs =200103 МПа.
Поперечная арматура (хомуты) класса A-I, Rs = 225 МПа, Rsw = 175 МПа, Еs =200103 МПа.
5.2.
РАСЧЁТ НАДКРАНОВОЙ ЧАСТИ КОЛОННЫ.
Размеры прямоугольного сечения: ширина b = 500 мм, высота h = 600 мм, а = а'= 40
мм, полезная высота h0 = h  а = 600  40 = 560 мм.
Подбор арматуры производим по расчетным усилиям:

Mmax  223.3 кНм;
N   708.8 кН;
Q   46.75 кН

Mmin  37.95 кНм;
N   521.0 кН;
Q   35.25 кН

Nmax   726.0 кН;
M  192.9 кНм;
Q   33.46 кН
Усилия от длительно действующей нагрузки Nℓ =  551.6 кН, Mℓ = 163 кНм.
Радиус инерции сечения:
I
h2
600 2
i


 173.2 мм.
A
12
12
Расчетная длина надкрановой части колонны с учета крановой нагрузки ℓо = 2Нв
= 23.9 = 7.8 м. Так как  = ℓo / i  7800 / 173.2 = 45.03 > 14, необходимо учесть влияние
прогиба на эксцентриситет продольной силы.
Эксцентриситет продольной силы при первой комбинации усилий:
eo = M / N = 223.3 / 708.8 = 0.32 м.
Случайный эксцентриситет
1
1
 ea   h   600  20 мм;
30
30
1
7800
 l0 
 13 мм;
 ea 
600
600
 ea  10 мм.
Принимаем eа = 2 cм.
Условная критическая сила равна:

6.4 E  I  0.11

N cr  2 b  
 0.1    J s  
 0    0.1  



где

6.4  29 109  90 104  0.11

 0.1  7 104   6433.84 кН,


2
7.8

 1.754  0.1  0.53

I  bh3 / 12  0.50.63 / 12  90104 м4
ℓ  1 + M1ℓ / M1  1 + 1306.42 / 406.59  1.754
M1ℓ  Mℓ + Nℓ(h / 2  a)  163.0 + 551.6(0.6 / 2  0.04)  306.42, кНм
M1  M + N(h / 2  a)  222.3 + 708.8(0.6 / 2  0.04)  406.59, кНм
  eo / h  0.32 / 0.60  0.53 > e,min  0.5  0.01ℓo / h  0.01Rbb2 
= 0.5  0.017.8 / 0.6  0.01171.1  0.183, принимаем   0.53
  Es / Eb  200103 / 29103  6.9,
Is  (As + A's)(h / 2a)2  bh0(h / 2a)2  6.90.0050.50.6(0.3  0.04)2 
= 710–4 м4
Коэффициент
  1 / (1  N / Ncr)  1 / (1  708.8 / 6433.84)  1.12
e  eo + eа+0.5h  a  0.321.12 +0.02+ 0.50.6  0.04  0.638 м
Граничное значение высоты сжатой зоны:

0.7
R 

 0.526
 sr 
 
365 
0.7 
1
 1 
 1 
 1

 sc,u  1.1 
400 
1.1 
где
    0.008Rbb2  0.85  0.008171.1  0.7
sr  Rs  365 МПа
sc,u  400 МПа, при b2 > 1
тогда 
R  R(1  0.5 R)  0.526(1  0.50.526)  0.388
Определяем площадь арматуры в сжатой зоне:
2
 N  e   r  Rb   b 2  h0  b
As 

Rsc  h0  a
708.8 103  0.638  0.388 17 106 1.1 0.56 2  0.5
 36.12 см 2  0.
6
365 10  0.56  0.04
Площадь сечения арматуры A'sназначается по конструктивным соображениям. Согласно СНиП минимальный процент армирования – 0.2%
A's  0.002bh0  0.0025056  5.6 см 2
Принимаем: 316 AIII с A's  6.03 см 2
Уточняем значение :

N  e  Rsc  As  h0  a 708.8 103  63.8  365 100  5.6  56  4


 0.118;
Rb   b 2  h02  b
17 100 1.1 56 2  50
соответствующее значение   0.126, тогда
R     b 2  h0  b  N
R
As  b
 As' sc 
Rsc
Rs
17 100 1.1  0.126  56  50  708.8 103
36500
 5.6
 4.26 см 2 .
365 100
36500
Площадь сечения арматуры Asназначается по конструктивным соображениям:
принимаем:
314 AIII с As  4.62 см2
Коэффициент армирован ия равен:
A  As' 4.62  6.03
 s

 0.00355 т.е.0.355%
bh
50  60
Так как мы задались  min  0.5 % и получили   0.355 % (сходимость близкая),
дальнейший расчёт не производим.
Выполним расчёт по второму сочетанию нагрузок.

Mmin  37.95 кНм;
N   521.0 кН;
Q   35.25 кН

Усилия от длительно действующей нагрузки Nℓ =  521,0 кН, Mℓ =37,95 Нм.
Эксцентриситет продольной силы при первой комбинации усилий:
eo = M / N = 37,95 / 521 = 0.073 м.
Случайный эксцентриситет
1
1
 ea   h   600  20 мм;
30
30
1
7800
 l0 
 13 мм;
 ea 
600
600
 ea  10 мм.
Принимаем eа = 2 cм.
Условная критическая сила равна:

6.4 E  I  0.11

N cr  2 b  
 0.1    J s  
 0    0.1  



6.4  29 109  90 104  0.11


 0.1  7 104   8844.12 кН,


2
7.8

 2  0.1  0.183

3
3
4
4

где
I  bh / 12  0.50.6 / 12  9010 м
ℓ  1 + M1ℓ / M1  1 + 1173.41 / 173.41  2
M1ℓ  Mℓ + Nℓ(h / 2  a)  37.95 + 521.0(0.6 / 2  0.04)  173.41, кНм
M1  M + N(h / 2  a)  37.95 + 521.0(0.6 / 2  0.04)  173.41, кНм
  eo / h  0.073 / 0.60  0.12 < e,min  0.5  0.01ℓo / h  0.01Rbb2 
= 0.5  0.017.8 / 0.6  0.01171.1  0.183, принимаем   0.183
  Es / Eb  200103 / 29103  6.9,
Is  (As + A's)(h / 2a)2  bh(h / 2a)2  6.90.0050.50.6(0.3  0.04)2 
–4 4
= 710 м
Коэффициент
  1 / (1  N / Ncr)  1 / (1  521 / 8844.12)  1.06
e  eo + eа+0.5h  a  0.0731.06 +0.02+ 0.50.6  0.04  0.357 м
Граничное значение высоты сжатой зоны:

0.7
R 

 0.526
 sr 
 
365 
0.7 
1
 1 
 1 
 1

 sc,u  1.1 
400 
1.1 
где
    0.008Rbb2  0.85  0.008171.1  0.7
sr  Rs  365 МПа
sc,u  400 МПа, при b2 > 1
тогда 
R  R(1  0.5 R)  0.526(1  0.50.526)  0.388
Определяем площадь арматуры в сжатой зоне:
2
 N  e   r  Rb   b 2  h0  b
As 

Rsc  h0  a
521103  0.357  0.388 17 106 1.1 0.56 2  0.5
 50.14 см 2  0.
6
365 10  0.56  0.04
Площадь сечения арматуры A'sназначается по конструктивным соображениям. Согласно СНиП минимальный процент армирования – 0.2%
A's  0.002bh0  0.0025056  5.6 см 2
Принимаем: 316 AIII с A's  6.03 см 2
Уточняем значение :

N  e  Rsc  As  h0  a 521103  35.7  365 100  5.6  56  4


 0.03;
Rb   b 2  h02  b
17 100 1.1 56 2  50
соответствующее значение   0.03, тогда
R     b 2  h0  b  N
R
As  b
 As' sc 
Rsc
Rs
17 100 1.1  0.03  56  50  521 103
36500

 5.6
 4.37 см 2 .
365 100
36500
Площадь сечения арматуры Asназначается по конструктивным соображениям.
As  0.002bh0  0.0025056  5.6 см 2
Принимаем: 316 AIII с As  6.03 см 2
Коэффициент армирования равен:
A  As' 2  6.03
 s

 0.004 т.е.0.4%
bh
50  60
Так как мы задались  min  0.5 % и получили   0.4 % (сходимость близкая), дальнейший расчёт не производим.
Выполним расчёт по третьему сочетанию нагрузок.

N мах  726.3 кН М  192.9 кНм Q  33.46 кН
Усилия от длительно действующей нагрузки Nℓ =  551,6 кН, Mℓ =163 Нм.
Эксцентриситет продольной силы при первой комбинации усилий:
eo = M / N = 192,9 / 726,3 = 0.266 м.
Случайный эксцентриситет
1
1
 ea   h   600  20 мм;
30
30
1
7800
 l0 
 13 мм;
 ea 
600
600
 ea  10 мм.
Принимаем eа = 2 cм.
Условная критическая сила равна:

6.4 E  I  0.11

N cr  2 b  
 0.1    J s  
 0    0.1  




6.4  29 109  90 104  0.11

 0.1  7 104   6818.69 кН,


2
7.8

 1.803  0.1  0.43

I  bh3 / 12  0.50.63 / 12  90104 м4
ℓ  1 + M1ℓ / M1  1 + 1306.42 / 381.74  1.803
M1ℓ  Mℓ + Nℓ(h / 2  a)  163.0 + 551.6(0.6 / 2  0.04)  306.42, кНм
M1  M + N(h / 2  a)  192,9 + 726,3(0.6 / 2  0.04)  381.74, кНм
  eo / h  0.266 / 0.60  0.43 > e,min  0.5  0.01ℓo / h  0.01Rbb2 
= 0.5  0.017.8 / 0.6  0.01171.1  0.183, принимаем   0.43
где
  Es / Eb  200103 / 29103  6.9,
Is  (As + A's)(h / 2a)2  bh(h / 2a)2  6.90.0050.50.6(0.3  0.04)2 
= 710–4 м4
Коэффициент
  1 / (1  N / Ncr)  1 / (1  726.3 / 6818.69)  1.12
e  eo + eа+0.5h  a  0.2661.12 +0.02+ 0.50.6  0.04  0.578 м
Граничное значение высоты сжатой зоны:

R 
1
где
 sr 
 
 1 

 sc,u  1.1 

0.7
 0.526
365 
0.7 
1
 1 

400 
1.1 
    0.008Rbb2  0.85  0.008171.1  0.7
sr  Rs  365 МПа
sc,u  400 МПа, при b2 > 1
тогда 
R  R(1  0.5 R)  0.526(1  0.50.526)  0.388
Определяем площадь арматуры в сжатой зоне:
2
 N  e   r  Rb   b 2  h0  b
As 

Rsc  h0  a
726.3 103  0.578  0.388 17 106 1.1 0.56 2  0.5
 37.82 см 2  0.
6
365 10  0.56  0.04
Площадь сечения арматуры A'sназначается по конструктивным соображениям. Согласно СНиП минимальный процент армирования – 0.2%
A's  0.002bh0  0.0025056  5.6 см 2
Принимаем: 316 AIII с A's  6.03 см 2
Уточняем значение :

N  e  Rsc  As  h0  a 726.3 103  57.8  365 100  5.6  56  4


 0.107;
Rb   b 2  h02  b
17 100 1.1 56 2  50
соответствующее значение   0.113, тогда
R     b 2  h0  b  N
R
As  b
 As' sc 
Rsc
Rs
17 100 1.1  0.113  56  50  726.3 103
36500
 5.6
 1.92 см 2 .
365 100
36500
Площадь сечения арматуры Asназначается по конструктивным соображениям.
Принимаем: 216 AIII с As  4.02 см 2
Коэффициент армирования равен:
A  As' 4.02  6.03
 s

 0.00335 т.е.0.335%
bh
50  60
Так как мы задались  min  0.5 % и получили   0.335 % (сходимость близкая),
дальнейший расчёт не производим.
Окончательно принимаем: 316 AIII с As  6.03 см 2
316 AIII с A's  6.03 см 2

5.3.
РАСЧЁТ ПОДКРАНОВОЙ ЧАСТИ КОЛОННЫ.
Она состоит из двух ветвей: высота всего сечения h  1200 мм, b  500 мм, сечение
ветвей: ширина bс = 500 мм, высота hс = 300 мм, h0 = 260 мм; расстояние между осями
распорок
s  2.5 м.
Подбор арматуры производим по расчетным усилиям в сечении II:

Mmax  522.4 кНм;
N   1639 кН;
Q   74.50 кН

Mmin  400.0 кНм;
N   1358 кН;
Q  18.22 кН

Nmax = 1639 кН;
M = 522.4 кНм;
Q   74.50 кН
Усилия от длительно действующей нагрузки Nℓ =  1097 кН, Mℓ = 83.22 кНм.
Расчетная длина подкрановой части колонны ℓо = 1.5Нн  1.510.95 = 16.425 м.
c2
0.95 2
i2 

 6.925  10 2 м 2
2
2




3  0.95
3c

41  2 2 2  4  1  2
2
2 
1
.
0

0
.
25

4
.
38

b
n


в


Так как  = ℓo / i  16.425 / 0.263 = 62.42 > 14, необходимо учесть влияние прогиба
на эксцентриситет продольной силы.
Выполним расчёт подкрановой части колонны по первому сочетанию нагрузок.
Находим усилия в сечениях ветвей колонны:
Nc  N / 2  M / c
Эксцентриситет продольной силы при первой комбинации усилий:
eo = M / N = 522.4 /1639 = 0.319 м.
Условная критическая сила равна:

6.4 E  I  0.11

N cr  2 b  
 0.1    J s  
 0    0.1  



6.4  29 109 1.731102  0.11


 0.1  9.73 104   3542.92 кН,


2
16.425  1.46  0.1  0.336


где
I  2bв hв i 2 = 20.250.56.925102  1.731102 м4
H н 10.95

 4.38
S
2.5
ℓ  1 + M1ℓ / M1  1 + 1604.395 / 1300.925  1.46
M1ℓ  Mℓ + Nℓс/2  83.32 + 10970.95/2  604.395, кНм
M1  M + Nс/2  522.4 + 16390.95/2  1300.925, кНм
  eo / с  0.319 / 0.95  0.336 > e,min  0.5  0.01ℓo / с  0.01Rbb2 
= 0.5  0.0116.425 / 0.95  0.01171.1  0.14, принимаем   0.336
n
  Es / Eb  200103 / 29103  6.9,
Is  bh(c / 2)2  6.90.0050.50.25(0.95/2)2  9.7310–4 м4
Коэффициент
  1 / (1  N / Ncr)  1 / (1  1639 / 3542.92)  1.86
Nc  N / 2  M / c
Продольные силы в наружной ветви: Nc1  1639/2 – 522.41.86/0.95  203.30 кН,
во внутренней ветви: Nc2  1639/2  522.41.86/0.95 = 1842.30 кН.
Изгибающий момент ветвей колонны равен:
Mc  Qs / 4  74.502.5 / 4  46.56 кНм.
eo  Mc / Nc2  45.56 / 1842.30  0.025 м
e  eo + hc / 2  a  0.025 + 0.25 / 2  0.04  0.11 м.
Ветви колонны испытывают действие одинаковых изгибающих моментов разных
знаков, поэтому подбираем симметричную арматуру.
Тогда при RscA'c = AsRs
  N c 2 /( Rb  b 2 bh0 )  1842.30103 / (171061.10.50.21)  0.94

0.7
R 

 0.526
 sr 
 
365 
0.7 
1
 1 
 1 
 1

 sc,u  1.1 
400 
1.1 
где
    0.008Rbb2  0.85  0.008171.1  0.7
sr  Rs  365 МПа
sc,u  400 МПа, при b2 > 1
Принимаем для расчёта    R  0.526 ,=> 
N  e    Rb   b 2  h02  b
As  As 

Rsc  h0  a

1842.30 103  0.11  0.390 17 106 1.1 0.212  0.5

 6.74 см 2
6
365 10  0.21  0.04
принимаем:
416 AIII с A's  As  8.04 см2.
Производим расчет промежуточной распорки. Изгибающий момент в распорке равен сумме моментов в двух ветвях, примыкающих к рамному узлу снизу и сверху:
Mp = QS /2  74.52.5 / 2  93.125 кНм.
Сечение распорки прямоугольное: b = 500 мм, h = 400 мм, ho = 360 мм.
Армируем сечение двойной симметричной арматурой:
Mp
93.125 103

As  As 

 7.97 cм 2 .
6
Rsc  h0  a 365 10  0.36  0.04
Принимаем 416 AIII с As  8.04 см2
Поперечная сила в распорке Qp = 2Mp/ c = 293.125 / 0.95  196.05 кН.
Так как  b 3 Rbt bh0  b , 2  0.6 1.2 10 6  0.5  0.36 1.1  142.56 < Qp  196.05 кН, то необходим расчёт поперечной арматуры.
Принимаем поперечную арматуру класса АI 26 c Rsw =175 МПа. Поперечную арматуру устанавливаем с шагом 100 мм.
g sw 
C0 
RSW ASW 175 100  0.57

 997.5 Н / см
S
10
b , 2 Rbt  b , 2bh02
g sw
2 1.2 100 1.1 50  36 2
 130.96 см
997.5

C w  2h0  2  36  72 см
Принимаем Сw = 72 см
Qb  Qsw  g swCw 
b , 2 Rbt bh02  b , 2
Cw
 997.5  72 
2 1.2 100  50  36 2 1.1
 309.42 кН >
72
Qp = 196.05 кН → условие выполняется. Устанавливаем хомуты 6AI с шагом 100 мм.
Выполним расчёт подкрановой части колонны по второму сочетанию нагрузок.
Находим усилия в сечениях ветвей колонны:
Nc  N / 2  M / c
Эксцентриситет продольной силы при первой комбинации усилий:
eo = M / N = 400 /1358 = 0.295 м.
Условная критическая сила равна:

6.4 E  I  0.11

N cr  2 b  
 0.1    J s  
 0    0.1  



6.4  29 109 1.731102  0.11


 0.1  9.73 104   3440.35 кН,


2
16.425  1.58  0.1  0.311


где
I  2bв hв i 2 = 20.250.56.925102  1.731102 м4
H н 10.95

 4.38
S
2.5
ℓ  1 + M1ℓ / M1  1 + 1604.395 / 1045.05  1.58
M1ℓ  Mℓ + Nℓс/2  83.32 + 10970.95/2  604.395, кНм
M1  M + Nс/2  400 + 13580.95/2  1045.05, кНм
  eo / с  0.295 / 0.95  0.311 > e,min  0.5  0.01ℓo / с  0.01Rbb2 
= 0.5  0.0116.425 / 0.95  0.01171.1  0.14, принимаем   0.311
n
  Es / Eb  200103 / 29103  6.9,
Is  bh(c / 2)2  6.90.0050.50.25(0.95/2)2  9.7310–4 м4
Коэффициент
  1 / (1  N / Ncr)  1 / (1  1358 / 3440.35)  1.65
Nc  N / 2  M / c
Продольные силы в наружной ветви: Nc1  1358/2 – 4001.65/0.95  15.74 кН,
во внутренней ветви: Nc2  1358/2  4001.65/0.95 = 1373.74 кН.
Изгибающий момент ветвей колонны равен:
Mc  Qs / 4  18.222.5 / 4  11.388 кНм.
eo  Mc / Nc2  11.388 / 1373.74  0.008 м
e  eo + hc / 2  a  0.008 + 0.25 / 2  0.04  0.093 м.
Ветви колонны испытывают действие одинаковых изгибающих моментов разных
знаков, поэтому подбираем симметричную арматуру.
Тогда при RscA'c = AsRs
  N c 2 /( Rb  b 2 bh0 )  1373.74103 / (171061.10.50.21)  0.7

0.7
R 

 0.526
 sr 
 
365 
0.7 
1
 1 
 1 
 1

 sc,u  1.1 
400 
1.1 
где
    0.008Rbb2  0.85  0.008171.1  0.7
sr  Rs  365 МПа
sc,u  400 МПа, при b2 > 1
Принимаем для расчёта    R  0.526 ,=> 
 N  e    Rb   b 2  h0  b
As  As 

Rsc  h0  a
2

1373.74 103  0.093  0.390 17 106 1.1 0.212  0.5
 5.33 см 2  0
365 106  0.21  0.04
Площадь сечения арматуры A's  Asназначается по конструктивным соображениям.
A's  As  0.002bch0  0.0025021  2.1 см2
принимаем:
212 AIII с A's  As  2.26 см2.
Производим расчет промежуточной распорки. Изгибающий момент в распорке равен сумме моментов в двух ветвях, примыкающих к рамному узлу снизу и сверху:
Mp = QS /2  18.222.5 / 2  22.775 кНм.
Сечение распорки прямоугольное: b = 500 мм, h = 400 мм, ho = 360 мм.
Армируем сечение двойной симметричной арматурой:
Mp
22.775 103

As  As 

 1.95 cм 2 .
6
Rsc  h0  a 365 10  0.36  0.04
Принимаем 48 AIII с As  2.01 см2
Поперечная сила в распорке Qp = 2Mp/ c = 222.775 / 0.95  47.95 кН.
Так как  b 3 Rbt bh0  b , 2  0.6 1.2 10 6  0.5  0.36 1.1  142.56 > Qp  47.95 кН, то расчёт
поперечной арматуры не нужен.
По конструктивным соображениям устанавливаем хомуты 6AI с шагом 100 мм.
Окончательно принимаем продольную арматуру:
 В ветвях - 416 AIII с A's  As  8.04 см2.
 В распорке - 416 AIII с A's = As  8.04 см2
Окончательно принимаем поперечную арматуру:
 В ветвях – устанавливаем хомуты 6AI с шагом 20d мм, равным 2016 =320 мм
 В распорке - устанавливаем хомуты 6AI с шагом 100 мм
6. РАСЧЁТ ВНЕЦЕНТРЕННО НАГРУЖЕННОГО ФУНДАМЕТА ПОД
КРАЙНЮЮ ДВУХВЕТВЕВУЮ КОЛОННУ.
6.1.
КОНСТРУКТИВНОЕ РЕШЕНИЕ. ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ
РАЗМЕРЫ.
Глубина заложения фундамента назначается не менее 1.5 м. Для возможности выполнения работ нулевого цикла до установки колонн принимается фундамент с высоким
расположением стакана. Отметка верха фундамента  0.150 м.
Глубина заделки колонны в стакан фундамента:
1. hз  0.5 + 0.33hн  0.5 + 0.331.2  0.896 м;
2. hз  1.5b  1.50.5  0.75 м.
Бетон класса В 20.
Продольная рабочая арматура класса АIII растянутой ветви должна быть заведена
за верхнюю грань стакана фундамента на длину не менее 30d  3016  480 мм.
Таким образом, минимальная высота фундамента Нmin  0.896 + 0.25  1.146 м.
Окончательно принимается Нф  1.5 м, что больше Нmin и соответствует требуемой
глубине заложения фундамента.
Требуемые размеры подколонника:
hп  hк + 275 + 2200  1200 + 150 + 400  1750 мм;
bп  bк + 275 + 2200  500 + 150 + 400  1050 мм.
В данном случае принимаются следующие размеры подколонника (кратные 300 мм):
hп  1800 мм, bп  1200 мм.
6.2.
ОПРЕДЕЛЕНИЕ НАГРУЗОК И УСИЛИЙ, ДЕЙСТВУЮЩИХ НА
ОСНОВАНИЕ И ФУНДАМЕНТ
Расчёт оснований по деформациям производится на основное сочетание нагрузок с
коэффициентом надёжности по нагрузке f  l, расчет фундамента по прочности — на основные (или особые) сочетания нагрузок с коэффициентами надежности по нагрузке f > l.
Наибольшие усилия от расчетных нагрузок (при f = 1 и f > 1), передаваемых колонной в уровне верха фундамента, приведены ниже.

N   1639 кН;
M  522.4 кНм; Q   74.50 кН
Усилия, действующие относительно оси симметрии подошвы фундамента (без учета
собственного веса фундамента и грунта на нем), определяем по формулам:
M = МI–I  QI–IHф  Gстeст;
N = NI–I + Gст,
где
МI–I, NI–I, QI–I — усилия в уровне верха фундамента; Сст — нагрузка от веса стены.
Нормативная нагрузка от массы стеновых панелей Gст=29.16 кН
Эксцентриситет е  стеновых панелей 750 мм.
Момент от веса стены:
Mw 29.160.75  21.87 кНм
Расчётные усилия в уровне подошвы фундамента:
M = 522.4  74.501.5  29.160.75 612.28 кНм;
N = 1639 + 29.16  1668.16 кН.
Нормативные усилия в уровне подошвы фундамента определяем приближенно:
M
612.28
M ser 

 501.87 кНм
 m,ser
1.22
N
1668.16
N ser 

 1367.34 кН
 m,ser
1.22
6.3.
ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ПОДОШВЫ ФУНДАМЕНТА.
Размеры подошвы фундаментов для зданий, перечисленных в табл. 19 СНиП II1574, определяются из условия, чтобы:
1) среднее давление на грунт под фундаментами проектируемых зданий не превышало расчетного давления на основание R;
2) краевое давление не превосходило 1.2 R;
3) в зданиях, оборудованных кранами грузоподъемностью менее 75 т, минимальное
краевое давление Pmin  0.
Расчет внецентренно загруженного фундамента ведется методом последовательного
приближения. Расчетное давление на основание и средний удельный вес фундамента и
грунта:
R0  240 кПа.
Требуемые размеры подошвы фундамента:
Аф  Nser / (1,2R0  срH)  1367,34 / (1,2240201.65)  5.36 м2,
где
ср — средний удельный вес материала фундамента и грунта (принимаемый обычно 20 кН / м3);
Н — глубина заложения фундамента, считая от планировочной отметки
земли около фундамента.
Назначаем отношение сторон подошвы фундамента: m  b / l  0.8. Тогда:
Аф
5.36
l

 2.59 м.
m
0.8
Назначаем ℓ  2.7 м, b  2.70.8  2.16 м. Принимаем подошву фундамента 2.7x2.4.
Площадь подошвы фундамента Аф  2.72.4  6.48 м2.
Момент сопротивления подошвы фундамента Wф  2.42.72 / 6  2.916 м3.
Напряжения в грунте (предполагаем линейное распределение напряжений):
max
 N / Aф  M / Wф  1668.16 / 6.48  612.28 / 2.916  257.43  209.97 кПа;
p min
рmax  257.43 + 209.97  467.4 кПа > 1.2 R0 =1.2240 =288 кПа
рmin  257.43  209.97  47.46 кПа > 0.
Необходимо увеличить размеры фундамента. Принимаем подошву фундамента
3.3x3.0. Площадь подошвы фундамента Аф  3.33  9.9 м2.
Момент сопротивления подошвы фундамента Wф  33.32 / 6  5.445 м3.
Напряжения в грунте (предполагаем линейное распределение напряжений):
max
 N / Aф  M / Wф  1668.16 / 9.9  612.28 / 5.445  168.50  112.45 кПа;
p min
рmax  168.50 + 112.45  280.95 кПа < 1.2 R0 =1.2240 =288 кПа
рmin  168.50  112.45  56.05 кПа > 0.
Условия выполняются, значит размеры подошвы приняты верно.
6.4.
РАСЧЁТ ТЕЛА ФУНДАМЕНТА.
Он включает расчёт на продавливание и установление высоты плитной части, а
также размеров ступеней фундамента; расчёт подколонника и его стаканной части; определение необходимой площади сечения арматуры у подошвы фундамента.
Назначаем высоту ступени равной h = 40 см.
L h
3.3  1.8
Определим вынос консоли c  ф п 
 0.75
2
2
Высота подколонника будет равна Нп = 1.5  0.4 = 1.1 м
Принимаем толщину защитного слоя а = 4 см, тогда рабочая высота нижней ступени
будет равна h0  h  a  40  4  36 см.
Размер нижнего основания пирамиды продавливания равен:
b  bп  2h0  120  2  36  192 см
Средняя линия пирамиды продавливания равна
b  bп 192  120
bср 

 156 см
2
2
Продавливающая сила равна F  Pmax A
bф  b
3  1.92
A
(c  h0 ) 
 (0.75  0.36)  0.9594 м 2
2
2
F  0.9594  280.95  269.54 кН
Величина поперечной силы, воспринимаемая бетоном равна
b ,3 Rbt  b , 2bср h0  0.6  0.9 100 1.1156  36  333.59 кН > F = 269.54 кН
При расчете подколонника и его стаканной части площадь сечения продольной арматуры определяем из расчета на внецентренное сжатие стенок стакана по нормальному
сечению АА, проходящему по торцу колонны
e0  M / N  612.28 / 1668.16  0.37 м
Расчет ведем для второго случая сжатия:
е = е0 + h / 2  а = 0.37 + 1.8 / 2  0.06 = 1.21 м.
Площадь сечения продольной арматуры
As  A's  (Ne   b , 2 RbS0 )/(Rszs)  (1668.161031.21  1.111.51001079460) /
(2251001.68) < 0,
где
S0 = 0.5(bпh02  aстbстzs) = 0.5(1201742  13565168) = 1079460 см3.
Минимальная площадь сечения продольной арматуры As  As'  0.0005bп hп Аs 
0.0005180120  10,8 см2. Принимаем 616АI (Аs  12,06 см2).
Поперечное армирование стакана принимаем в виде горизонтальных сварных сеток. Поперечная арматура подколонника в наклонном сечении В—В определяется по расчету на момент от действующих сил относительно оси, проходящей через точку К.
Расстояние у от оси колонны до условной оси поворота колонны и площадь сечения поперечной арматуры стенок стакана Аw
при hн / 6 < e0 < hн / 2, у  0,7e0:
при e0  hн / 2; уhн / 2:
Aw 
M  Qh з  N 0.7e0  Gст (ест  у )
;
Rs  z w
h


0.8 M  Qhз  N п  Gст (ест  у )
2

;,
Aw 
Rs  z w
при e0< hн / 6 поперечное армирование стенок стакана назначают конструктивно.
где
Aw — площадь сечения всех поперечных стержней одной сетки;
zw — расстояние от торца колонны до поперечных стержней сеток;
0,8 — коэффициент, учитывающий влияние продольной арматуры.
В нашем случае e0 = 0.37 м < hн / 6 = 1.8/6 = 0.3 м, то есть поперечное армирование
необходимо определять расчетом.
Устанавливаем 7 сеток поперечного армирования с шагом по высоте 100 мм.
z = 0.85 + 0.75 + 0.65 + 0.55 + 0.45  035  0.25 = 3.85м.
у  0,7e0 = 0,737 = 25.9 см
Aw 
M  Qhз  N 0.7e0  Gст (ест  у )

Rs  z w
612.28 105  74.50 103  90  0.7  37 1668.16 103  29.16 103  (75  25.9)

 3.02 см 2 ;
225 100  385
;
Принимаем для сетки арматуру 410 A-I. As = 3.14 см2.
При определении площади сечения арматуры подошвы фундамента площадь поперечного сечения рабочей арматуры определяется из расчета на изгиб консольного выступа
фундамента в сечениях по граням ступеней фундамента и по грани колонны (см. рис. 3.1).
Напряжения в грунте (предполагаем линейное распределение напряжений):
max
 срН + Nser / Aф  Mser / Wф  201.65 + 1367.34 / 9.9  501.87 / 5.445  171.11  92.17
p min
кПа;
рmax  171.11 + 92.17  263.28 кПа < 1.2 R0 =1.2240 =288 кПа
рmin  171.11  92.17  78.94 кПа. > 0.
Арматура, укладываемая параллельно большей стороне фундамента, определяется
по изгибающему моменту, действующему в сечении II:
M1 = 0.125( Lф  hп ) 2 Pmax bф = 0.125(3.31.8)2263.283 = 222.14 кНм;
α = (1 – 0.5) = M1 / (  в , 2 Rbbh20)  222.14105 / (1.111.5100270362)  0.05;
v = 1 – 0.5 = 0.975;
Аs  222.14 / (2251030.9750.36) = 28.13 cм2
Принимаем 1616AI (As = 32.176 cм2).
Арматуру устанавливаем с шагом 14x20  1x12.
Арматура, укладываемая параллельно меньшей стороне фундамента, определяется
по изгибающему моменту в сечении IIII:
M2 = 0.125( Bф  bп ) 2 Pcp Lф = 0.125(31.2)292.173.3 = 123.19 кНм;
α = (1 – 0.5) = M2 / ((  в , 2 Rbbh20)  123.19105/ (1.111.5100300362)  0.025;
v = 1 – 0.5 = 0.987;
Аs  123.19 / (2251030.9870.36)  142710-6 м2 = 15.41 cм2
Принимаем 2310AI (As = 18.055 cм2).
Арматуру устанавливаем с шагом 20x15  2x11.
Приложение 1
Кафедра "Железобетонные и каменные конструкции"
Cтатический расчет одноэтажной рамы по КП
"Одноэтажное производственное здание "
Працуто М.И. гр. 112157 (шифр расчета - MI)
*** Общие данные по расчету ***
1 - Количество пролетов
22.00 - Pазмер пролета в осях, м
10.95 - Расстояние от обреза фунд-та до верха консоли, м
3.90 - Высота надкрановой части колонны, м
1.20 - Высота подкрановой балки, м
250.0 - Привязка крайней колонны, мм
29000.0 - Модуль упругости бетона колонн, МПа
*** Форма и размеры сечения колонн, мм ***
5
- Код сечения подкрановой части КРАЙНЕЙ колонны - сквозное (коробчатое)
500.0 1200.0 - Ширина и высота сечения подкрановой части
250.0 - Высота сечения ветви подкрановой части колонны
600.0 - Высота сечения надкрановой части
*** Нагрузки ***
75.52 - Нагрузка от собственного веса подкрановой части КРАЙНЕЙ колонны, KH
30.57 - Нагрузка от собственного веса надкрановой части КРАЙНЕЙ колонны, KH
462.74 - Нагрузка на крайнюю колонну от собственного веса покрытия, KH
0.140 - Эксцентриситет ee приложения относительно оси надкрановой части, m
58.32 - Нагрузка от собственного веса парапетной панели, KH
390.96 - Нагрузка от собственного веса стеновой панели, KH
300.000 - Толщина стеновых панелей, мм
79.17 - Нагрузка от собственного веса подкрановой балки, KH
0.400 - Эксцентриситет ее приложения относит. оси подкрановой части
крайней колонны, m
174.68 - Нагрузка на крайнюю колонну от веса снегового покрова, KH
6.21 - Сосредоточенная активная нагрузка от давления ветра W, kH
2.92 - Распределенная активная нагрузка от давления ветра w, kH/m
4.66 - Сосредоточенная пассивная нагрузка от давления ветра W', kH
2.19 - Распределенная пассивная нагрузка от давления ветра w', kH/m
427.25 115.47 - Крановая нагрузка (Dmax Dmin), KH
12.30 - Haгрузка от торможения крана, KH
Працуто М.И. гр. 112157
Кафедра "Железобетонные и каменные конструкции"
Cтатический расчет одноэтажной рамы для КП-2
"Одноэтажное производственное здание"
РАЗДЕЛ 9.УСИЛИЯ/НАПРЯЖЕНИЯ/ В
ЭЛЕМЕНТАХ
3. 4.2001
10:34:27 Працуто М.И. НИИАСС ЛИРА-ПК (В. 1.0 )
1
-------------------------------------------------------------------------------------------------------------------------------I
У С И Л И Я / Н А П Р Я Ж Е Н И Я / В Т,ТМ,ТММ
I
-------------------------------------------------------------------------------------------------------------------------------I
2 I
1-1:
1-2:
3-1:
3-2:
4-1:
4-2:
I
I
1 :
1 :
3 :
3 :
4 :
4 :
I
I
2 :
2 :
4 :
4 :
5 :
5 :
-------------------------------------------------------------------------------------------------------------------------------I 1- I
I
I N
I-109.73 -102.18 -55.164 -54.223 -54.223 -52.106
I
I M
I 8.3324 -26.790 16.305 12.456 12.456 3.7954
I
I Q
I-3.2075 -3.2075 -3.2075 -3.2075 -3.2075 -3.2075
I
I 2- I
I
I N
I-17.468 -17.468 -17.468 -17.468 -17.468 -17.468
I
I M
I -.7351 -2.2539 2.9865 2.8200 2.8200 2.4455
I
I Q
I -.1387 -.1387 -.1387 -.1387 -.1387 -.1387
I
I 3- I
I
I M
I 37.451 3.6006 3.6006 2.0197 2.0197
I
I Q
I-4.6900 -1.4926 -1.4926 -1.1422 -1.1422 -.3538
I
I 4- I
I
I M
I-35.035 -4.5249 -4.5249 -2.7778 -2.7778
I
I Q
I 3.9853 1.5873 1.5873 1.3245 1.3245
.7332
I
I 5- I
I
I N
I-42.725 -42.725
I
I M
I 3.3046 13.470 -3.6204 -2.5064 -2.5064
I
I Q
I .9283
.9283
.9283
.9283
.9283
.9283
I
I 6- I
I
I N
I-11.547 -11.547
I
I M
I-9.1664
.9986 -3.6204 -2.5064 -2.5064
I
I Q
I .9283
.9283
.9283
.9283
.9283
.9283
I
I 7- I
I
I M
I-8.7734
.1447
.1447 1.1220 1.1220
I
I Q
I .8144
.8144
.8144
.8144 -.4156 -.4156
I
I 8- I
I
I M
I-6.1711 -1.6207 -1.6207 -1.1220 -1.1220
I
I Q
I .4156
.4156
.4156
.4156
.4156
.4156
I
9.
РАЗДЕЛ 11. РАСЧЕТНЫЕ СОЧЕТАНИЯ УСИЛИЙ И УНИФИКАЦИЯ.
11.
21. 4.1998
9:28:28 Працуто НИИАСС ЛИРА-ПК (В. 1.0)
1
-----------------------------------------------------------------------------------------I
РАСЧЕТНЫЕ СОЧЕТАНИЯ УСИЛИЙ(НАПРЯЖЕНИЙ) В Т ТМ И ТММ
I
-----------------------------------------------------------------------------------------: ЭЛМ:СЧ:ПР:КР:СН:КС: N
P: M
P: Q
P: N
Д: М
Д: Q
Д: НОМЕРА ЗАГРУЖЕНИЙ Р.С.У.
I
-----------------------------------------------------------------------------------------I
1 1 1 1 1
:-109.7 45.78 -7.897 -109.7 8.332 -3.207
1
3
I
I
2
2 K :-135.8 -40.00
1.822 -109.7
8.332 -3.207
1
2
4
6
7
I
6
2 K :-163.9
52.24 -7.450 -109.7
8.332 -3.207
1
2
3
5
7
I
13
2 K :-120.1 -39.34
1.947 -109.7
8.332 -3.207
1
4
6
7
I
18
2 K :-163.9 -28.78
1.822 -109.7
8.332 -3.207
1
2
4
5
I
29
2 K :-148.1 -28.12
1.947 -109.7
8.332 -3.207
1
4
5
7
8.332 -3.207
1
3
.254 -109.7
8.332 -3.207
1
2
4
41.37 -7.553 -109.7
8.332 -3.207
1
2
3
.777 -109.7
8.332 -3.207
1
4
7.597 -3.346 -109.7
8.332 -3.207
1
2
I
I
I
7
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
14= 1
30= 1
I
I
1
1
1 51
1
:-109.7
45.78 -7.897 -109.7
I
52
2
:-125.4 -23.86
I
56
2
:-125.4
I
63
1
:-109.7 -26.70
I
68
1
:-127.2
I
I
I
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
64=51
79=63
80=51
I
I
1
2
1
2
2 K :-128.2 -33.45
-.694 -102.1 -26.79 -3.207
1
2
4
6
8
I
6
2 K :-156.3 -11.99 -4.214 -102.1 -26.79 -3.207
1
2
3
5
8
I
14
1
1
3
I
18
2 K :-156.3 -22.22
-.694 -102.1 -26.79 -3.207
1
2
4
5
8
I
I
:-102.1 -23.18 -4.700 -102.1 -26.79 -3.207
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
30=14
I
I
1
2
1 52
2
:-117.8 -32.89 -1.903 -102.1 -26.79 -3.207
1
2
4
I
56
2
:-117.8 -25.57 -4.675 -102.1 -26.79 -3.207
1
2
3
I
64
1
:-102.1 -23.18 -4.700 -102.1 -26.79 -3.207
1
3
I
68
1
:-119.6 -29.04 -3.346 -102.1 -26.79 -3.207
1
2
I
I
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
80=64
I
I
3
1
1
1
2
:-70.88
22.23 -4.675 -55.16
16.30 -3.207
1
2
I
14
1
:-55.16
19.90 -4.700 -55.16
16.30 -3.207
1
3
I
18
1
:-72.63
19.29 -3.346 -55.16
16.30 -3.207
1
2
3
I
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
6= 1
30=14
I
I
3
1
1 51
2
:-70.88
22.23 -4.675 -55.16
16.30 -3.207
1
2
I
64
1
:-55.16
19.90 -4.700 -55.16
16.30 -3.207
1
3
I
68
1
:-72.63
19.29 -3.346 -55.16
16.30 -3.207
1
2
3
I
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
56=51
80=64
I
I
3
2
1
1
2
:-69.94
16.81 -4.360 -54.22
12.45 -3.207
1
2
18
1
:-71.69
15.27 -3.346 -54.22
12.45 -3.207
1
2
I
I
I
3
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
6= 1
14= 1
30= 1
I
I
3
2
1 51
2
:-69.94
16.81 -4.360 -54.22
12.45 -3.207
1
2
68
1
:-71.69
15.27 -3.346 -54.22
12.45 -3.207
1
2
3
I
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
56=51
64=51
80=51
I
I
4
1
1
1
2
:-69.94
16.81 -4.360 -54.22
12.45 -3.207
1
2
18
1
:-71.69
15.27 -3.346 -54.22
12.45 -3.207
1
2
3
I
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
6= 1
14= 1
30= 1
I
I
4
1
1 51
2
:-69.94
16.81 -4.360 -54.22
12.45 -3.207
1
2
68
1
:-71.69
15.27 -3.346 -54.22
12.45 -3.207
1
2
3
I
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
56=51
64=51
80=51
I
I
4
2
1
2
2
:-52.10
3.795 -3.525 -52.10
3.795 -3.207
1
3
I
6
1
:-69.57
6.240 -3.346 -52.10
3.795 -3.207
1
2
I
14
2
:-67.82
5.996 -3.650 -52.10
3.795 -3.207
1
2
I
I
3
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
18= 6
30=14
I
I
4
2
1 52
2
:-52.10
3.795 -3.525 -52.10
3.795 -3.207
1
3
I
56
1
:-69.57
6.240 -3.346 -52.10
3.795 -3.207
1
2
I
64
2
:-67.82
5.996 -3.650 -52.10
3.795 -3.207
1
2
I
I
I
IЭКВИВАЛЕНТНЫЕ СОЧЕТАНИЯ
I
68=56
80=64
3
ЛИТЕРАТУРА
1) Байков В. Н., Сигалов Э. Е. Железобетонные конструкции. Общий курс.
2) Дрозд Я. И., Пастушков Г. П. Предварительно напряжённые железобетонные
конструкции.
3) СНиП 2.03.0184 Строительные нормы и правила Ч. II. Нормы проектирования. Бетонные и железобетонные конструкции.
4) СНиП 2.01.07-85. Нагрузки и воздействия/Госстрой СССР. – М.: ЦИТП, Госстроя СССР, 1987.
5)
Конспект лекций.