А.А. Прокофьев, Е.А. Разинкова,
Т.В. Соколова, С.С. Карташёв
МАТЕМАТиКА
БАзоВый уРоВЕнь
ЕДиный ГоСуДАРСТВЕнный
ЭКзАМЕн
ГоТоВиМСЯ К иТоГоВой АТТЕСТАЦии
Электронное издание
Москва
Издательство «Интеллект-Центр»
2024
Рецензенты:
Т. Н. Казарихина – кандидат педагогических наук, заместитель директора по НМР,
АНО СОШ «Димитриевская», доцент МПГУ;
Е. В. Лукьянова – кандидат педагогических наук, доцент кафедры математического анализа МПГУ,
учитель высшей категории
Прокофьев, А. А.
Математика. Базовый уровень. Единый государственный экзамен. Готовимся к итоговой
аттестации / А. А. Прокофьев, Е. А. Разинкова, Т. В. Соколова, С. С. Карташёв. — Эл. изд. —
1 файл pdf : 271 с. — Москва : Издательство «Интеллект-Центр», 2024. — (Единый государственный экзамен). — Систем. требования: Adobe Reader XI либо Adobe Digital Editions 4.5 ;
экран 10". — Текст : электронный.
Данное пособие предназначено для подготовки к Единому государственному экзамену по математике базового уровня. Издание включает типовые задания по всем содержательным линиям экзаменационной работы, а также 30 тренировочных вариантов в формате ЕГЭ 2023 года.
Пособие поможет школьникам проверить свои знания и умения по предмету, а учителям — оценить
степень достижения требований образовательных стандартов отдельными учащимися и обеспечить их
целенаправленную подготовку к экзамену.
УДК 373.167.1:51(075.3)
ББК 22.1я721
Электронное издание на основе печатного издания: Математика. Базовый уровень. Единый государственный экзамен.
Готовимся к итоговой аттестации / А. А. Прокофьев, Е. А. Разинкова, Т. В. Соколова, С. С. Карташёв. — Москва :
Издательство «Интеллект-Центр», 2024. — 272 с. — (Единый государственный экзамен). — ISBN 978-5-907651-555. — Текст : непосредственный.
© ООО «Издательство «Интеллект-Центр», 2024
© А.А. Прокофьев, Е.А. Разинкова, Т.В. Соколова,
С.С. Карташёв, 2023
Предисловие
Данное пособие предназначено для подготовки к единому государственному экзамену (ЕГЭ) по
математике базового уровня, проводимом в 11 классе, и может быть использовано как учителями
математики при подборе заданий для занятий по подготовке к такому экзамену, так и самими обучающимися для отработки навыков решения заданий ЕГЭ по математике базового уровня. Также
пособие будет полезным для любого читателя, который хочет укрепить свои знания по той или иной
математической теме.
Пособие содержит задания по всем темам курса математики, встречающимся в ЕГЭ по математике
базового уровня, проверочные работы по отдельным темам, 30 тренировочных вариантов и справочные материалы. Также в пособие включены задания, аналогичные по математическому содержанию
заданиям Открытого банка заданий на сайте fipi.ru и демоверсии ЕГЭ по математике базового уровня
2024 года.
Первая глава содержит задания по различным темам алгебры и началам математического анализа,
а также задачи по теории вероятностей и статистике. Все задания этой главы состоят из нескольких пунктов, содержащих однотипные задания. Удобно строить работу с ними следующим образом:
первый пункт разбирается учителем на уроке, а остальные пункты могут быть использованы для
организации самостоятельной работы обучающихся на уроке, а также для включения этих пунктов
в домашнее задание.
Вторая глава посвящена отработке навыков решения геометрических задач. В ней представлены
задачи прикладного содержания как по планиметрии, так и по стереометрии. Также глава включает
набор стандартных геометрических задач, аналоги которых входят в ЕГЭ по математике базового
уровня. В этой главе все задания тоже состоят из нескольких пунктов.
Каждая глава содержит проверочные работы для контроля уровня усвоения обучающимися отдельных тем.
Более подробно соответствие параграфов/пунктов пособия и заданий вариантов ЕГЭ приведено
в таблице.
Задание ЕГЭ
Номер параграфа/пункта
Задание ЕГЭ
1
2
п. 4.3 п. 4.1
12
13
3
4
5
6
7
§5
п. 4.2
§6
п. 4.5
§5
14
15
16
Номер парап. 7.2–7.4 п. 8.2 п. 1.1 п. 4.4 п. 1.2–1.5
графа/пункта
17
§2
8
9
10
11
п. 4.7 п. 7.1 п. 7.1 п. 8.1
18
19
20
21
п. 1.6; §3 п. 1.7 п. 4.6 п. 4.8
В пособии вы найдёте 30 тренировочных вариантов, среди которых есть варианты с похожими
заданиями, что можно использовать при проведении внутришкольных тренировочных работ в формате ЕГЭ.
Надеемся, что пособие поможет вам отлично подготовиться к ЕГЭ по математике базового уровня!
Желаем успеха!
3
Глава 1. алГеБра, НаЧала МаТеМаТиЧесКоГо аНалиЗа,
ТеориЯ вероЯТНосТеЙ и сТаТисТиКа
§ 1. Числа и вычисления
1.1. дроби
1.
2.
3.
Найдите значения выражений.
а) 9,5 ⋅ 1,6 + 4,3 ;
б) 7,5 ⋅ 3,6 − 1,9 ;
в) 0, 21 ⋅ 0,5 − 0,037 ;
г) 5,5 ⋅ 6, 2 − 0,8 ;
д) 7,5 ⋅ 3,6 + 2,74 ;
е) 4,1 ⋅ 6,9 + 0,71 .
Найдите значения выражений.
а) (4,9 − 3, 4) ⋅ 8, 2 ;
б) (1,7 + 2,8) ⋅ 4,3 ;
в) (5,8 − 3,3) ⋅ 3, 4 ;
г) (4, 2 + 1,3) ⋅ 36 ;
д) (3, 2 + 6,8) ⋅ 3,1 ;
е) (1,3 + 3, 2) ⋅ 5, 2 .
Найдите значения выражений.
а)
4.
1
⋅ 0,77 + 2, 22 ;
7
1
⋅ 12,6 − 1 ;
6
в)
1
⋅ 6, 4 − 1 ;
4
г) 0,33:
11
+ 3,14 .
17
Найдите значения выражений:
а) 7
5.
б)
11
7
3
−6 +3 ;
16
8
4
б) 8
21
5
3
−5 +9 ;
40
8
5
в) 2
13
7
8
9
2
123
+ 4 − 23
; г) 9 + 3 − 15
.
20
40
500
16
5
200
Найдите значения выражений.
9 5 4
+ : ;
8 2 7
3 7 2
д) + ⋅ ;
5 2 5
7 11 3
и) : − ;
5 10 11
7 15 2
+ : ;
8 4 3
7
3 15
е)
+ ⋅ ;
26 13 2
15 3 3
к)
;
⋅ −
4 7 28
а)
3 7 7
+ : ;
4 12 3
7 5 7
ж)
+ ⋅ ;
16 8 2
7 7 1
л) ⋅ − ;
3 4 12
б)
в)
11 9 2
+ ⋅ ;
5 5 3
7 5 13
з) : − ;
3 4 15
7 11 5
м) ⋅ − .
2 9 18
г)
6. Найдите значения выражений
а)
7.
8.
29 15 5
⋅ : ;
54 4 9
б)
34 85 26
: ⋅ ;
65 27 54
в)
Найдите значения выражений:
1
1
а)
;
б)
;
1 1
1
1
−
−
9 11
13 23
Найдите значения выражений.
а)
8,5 − 3,7
;
2, 4
б)
в)
4, 4 + 3,1
;
0,3
9,0
1, 2 + 9,3
;
д)
;
4,1 − 2,6
1,5
Найдите значения выражений:
г)
9.
а)
4
4,8 ⋅ 1,8
;
7, 2
б)
3,5 ⋅ 2, 4
;
5,6
в)
9 18 15
: : ;
40 75 4
4
;
1 1
−
14 10
в)
6,1 − 4,9
;
1, 2
е)
11,7
.
5, 2 − 1,3
0,62 ⋅ 5, 4
;
12, 4
7 2 35
: : .
30 5 3
г)
г)
г)
2
.
1
1
−
35 30
0,14 ⋅ 3, 2
.
1, 28
10. Найдите значения выражений:
4 7 51
а) + : ;
5 4 20
13 11 1
б) − : ;
5 6 30
17 1 1
в) − : ;
4 8 32
3 3
г) − ⋅ 14 ;
4 7
3 1
д) − ⋅ 20 .
5 8
11. Найдите значения выражений:
2
2
5
1
а) 33 ⋅ − 5 ⋅ ;
11
11
5
1
б) 13 ⋅ + 51 ⋅ ;
17
17
3
3
2
3
1
1
г) 11 ⋅ + 98 ⋅ .
в) 81 ⋅ − 14 ⋅ ;
9
7
9
7
12. Найдите значения выражений:
а)
1, 4
;
1
5−
3
б)
2,6
;
1
3−
9
в)
0,13
;
4
1+
9
г)
0,17
.
6
4+
7
13. Найдите значения выражений:
а)
2, 2 − 7,6
;
2,7 ⋅ 0, 4
б)
3, 2 − 6,7
;
2,8 ⋅ 0, 25
в)
0,06 − 0,17
;
0,55 ⋅ (−0, 2)
г)
0, 4 − 0,19
.
−2, 4 ⋅ 0,5
14. Найдите значение выражения:
а) −3
1
2
б) −11 − 10 :1,6 ;
3
3
2
5
+ 4, 4 ⋅ − ;
13
26
3
7
в) 4,5 ⋅ − + 1 ;
15 25
г) 3
2 7
− : 0,13 .
13 25
15. Найдите значения выражений.
а) 0,36 ⋅
5 15 3
+ ⋅ ;
12 18 25
б) 0,32 ⋅
7 15 3
− ⋅
;
16 9 25
в) 0, 44 ⋅
6 8 13
5 35 9
+ ⋅ ; г) 0,38 ⋅ + ⋅ .
11 52 16
19 36 5
Проверочная работа № 1
Вариант 1
Найдите значения выражений:
1. а)
19,34 − 9,3
;
50, 2
18 29
2. а) 11 − 9 ⋅ ;
29 80
б)
5,1 ⋅ 5,6
;
6,8
б) 1
в) 1, 25 ⋅ 8,7 ⋅ 8 .
41 3
: 7 − 5 ;
64 16
в)
42 93 14
⋅ : ;
31 25 75
г)
4
.
1
1
−
19 21
5
Вариант 2
Найдите значения выражений:
1. а)
23,56 − 3,5
;
0,02
б)
16 74
2. а) 24 − 22 ⋅ ;
37 29
8, 4 ⋅ 7,7
;
13, 2
б) 3
в) 40 ⋅ 18,9 ⋅ 0, 25 .
11 7
:5 − 4 ;
48 24
в)
56 14 16
: : ;
81 15 27
г)
6
.
1 1
−
11 17
1.2. степень с целым показателем
16. Найдите значения выражений:
а) 3−12 ⋅ 314 ;
б) 7 −23 ⋅ 7 26 ;
в) 235 ⋅ 2−38 ;
г) 537 ⋅ 5−40 .
17. Найдите значения выражений:
313
225
;
б) 21 ;
10
2
3
18. Найдите значения выражений:
а)
а) 257 ⋅ 12511 : 547 ;
в)
б) 8116 : 930 : 34 ;
534
;
536
г)
441
.
443
в) 812 :16−4 : 3210 ;
г) 216−13 ⋅ 3612 : 6−16 .
19. Найдите значения выражений:
а) 0, 257 ⋅ 47 ;
б) 0,0213 ⋅ 5013 ;
в) 0,1253 ⋅ 0,83 ;
г) 4004 ⋅ 0,0254 .
20. Найдите значения выражений:
(7 −7 ) 4 ⋅ 715
915 ⋅ 9−42
;
б)
;
7 −13
(99 ) −3
21. Найдите значения выражений:
а)
в)
(312 ) −3 ⋅ 329
;
3−11
г)
(4−15 )5 ⋅ 459
.
4−14
а) 0,03 ⋅ 103 + 0,5 ⋅ 103 + 0,007 ⋅ 103 ;
б) 7 ⋅ 10−1 + 8 ⋅ 10−2 + 5 ⋅ 10−4 ;
в) 0,8 ⋅ 104 + 0,02 ⋅ 103 + 0,007 ⋅ 102 ;
г) 4 ⋅ 10−2 + 9 ⋅ 10−4 + 7 ⋅ 10−5 .
22. Найдите значения выражений:
а) (6 ⋅ 109 ) 2 ⋅ (2 ⋅ 10−6 )3 ;
б) (25 ⋅ 10−3 ) 2 ⋅ (5 ⋅ 10−2 ) −4 ;
в) (2 ⋅ 10−5 )3 ⋅ (4 ⋅ 1018 ) ;
г) (49 ⋅ 1012 )3 ⋅ (7 ⋅ 1010 ) −4 .
23. Найдите значения выражений:
а) (0,003 ⋅ 103 ) 2 + (0,07 ⋅ 102 ) 2 ;
б) (0,05 ⋅ 103 )3 − (0, 2 ⋅ 102 ) 2 ;
в) (0,002 ⋅ 104 ) 2 + (0,11 ⋅ 102 ) 2 ;
г) (0,004 ⋅ 103 )3 − (0,3 ⋅ 102 ) 2 .
24. Найдите значения выражений:
6
а) 3,5 ⋅ (−10)3 + 0,54 ⋅ (−10) 4 ;
б) 7 ⋅ (−0,1) 2 − 5 ⋅ (−0,1)3 ;
в) 0,036 ⋅ (−10)5 + 0, 4 ⋅ (−10) 4 ;
г) 400 ⋅ (−0,1)5 − 70 ⋅ (−0,1) 4 .
Проверочная работа № 2
Вариант 1
Найдите значения выражений:
1. а)
(6−5 )9 ⋅ 615
;
6−32
б) 8−4 ⋅ 165 : 320 .
2. а) 0,005 ⋅ 104 + 0,07 ⋅ 103 − 0, 4 ⋅ 101 ;
б) 12 ⋅ 10−4 + 6 ⋅ 10−2 + 8 ⋅ 10−1 .
3. (−0,1)3 − (−0, 2) 2 + (−0,6)0 .
Вариант 2
Найдите значения выражений:
1. а)
(53 )16 ⋅ 5−54
;
5−4
б) 810 ⋅ 27 6 : 97 .
2. а) 0,0009 ⋅ 106 + 0,002 ⋅ 105 − 0,6 ⋅ 102 ;
б) 8 ⋅ 10−5 + 61 ⋅ 10−3 + 7 ⋅ 10−2 .
3. (−0,3) 4 − (−0,1)3 − (−0,0004)0 .
1.3. иррациональные числа
25. Найдите значения выражений:
а)
14400 ;
б)
25600 ;
в)
0,0009 ;
г)
0,000625 ;
в)
6
19
;
25
г)
1
72 .
4
в)
0, 44 ⋅ 99 ;
г)
0,0012 ⋅ 75 .
5,8 ⋅ 0, 29 ⋅ 5 ;
г)
0, 45 ⋅ 0,625 ⋅ 8 .
в)
7 2 ⋅ 28 ;
г)
52 ⋅ 124 .
в)
252
;
700
г)
405
.
500
в)
33
;
(2 11) 2
г)
34
.
(5 17) 2
д)
8, 41 ;
е)
2, 25 .
26. Найдите значения выражений:
57
1
;
б) 5 ;
64
16
27. Найдите значения выражений:
а)
1
а)
18 ⋅ 72 ;
б)
15 ⋅ 60 ;
28. Найдите значения выражений:
а)
2,6 ⋅ 3,9 ⋅ 6 ; б)
4,5 ⋅ 7,5 ⋅ 15 ; в)
29. Найдите значения выражений:
а)
36 ⋅ 24 ;
б)
4 4 ⋅ 56 ;
30. Найдите значения выражений:
363
512
;
б)
;
3
32
31. Найдите значения выражений:
а)
(5 7) 2
(9 3) 2
;
;
б)
14
12
32. Найдите значения выражений:
а)
а)
1452 − 1442 ; б)
822 − 802 ;
в)
2,62 − 2, 42 ;
г)
2,52 − 0,7 2 .
7
33. Найдите значения выражений:
а) ( 17 − 3) ⋅ (3 + 17) ;
б) (8 − 43) ⋅ ( 43 + 8) ;
в) (5 + 31) ⋅ ( 31 − 5) ;
г) (12 + 94) ⋅ ( 94 − 12) .
34. Найдите значения выражений:
а) (3 50 − 2 18) ⋅ 32 ;
б) (8 28 − 3 63) : 7 ;
в) (5 27 + 4 12) ⋅ 75 ;
г) (6 44 + 99) : 11 .
Проверочная работа № 3
Вариант 1
Найдите значения выражений:
1. а)
1, 44 ;
2. а)
4, 2 ⋅ 7,5 ⋅ 14 ;
3. а)
852 − 842 ;
б)
11
;
в)
25
(3 13) 2
.
б)
52
1
72 ⋅ 50 ;
б) (5 + 57) ⋅ ( 57 − 5) ;
г)
28 ⋅ 36 .
в) (7 45 − 6 20) ⋅ 5 .
Вариант 2
Найдите значения выражений:
17
2
1. а) 1,96 ;
б)
16 ;
в)
28 ⋅ 63 ;
г)
34 ⋅ 46 .
69
.
(2 23) 2
2. а)
5, 2 ⋅ 3,9 ⋅ 27 ;
б)
3. а)
1132 − 1122 ;
б) (9 − 61) ⋅ ( 61 + 9) ;
в) (8 24 + 3 54) ⋅ 6 .
1.4. логарифмы
35. Найдите значения выражений:
а) log 5 625 ;
б) log 216 ;
д) log17 1 ;
е) log 0,5 32 ;
1
;
27
ж) lg 0,01 ;
в) log 3
г) log 4 0, 25 ;
з) lg1000 .
36. Какое из чисел является отрицательным? В ответе укажите цифру выбранного варианта.
7
1
4) log 0,2 9 .
;
3) log 6 ;
3
7 4
37. Какое из чисел является положительным? В ответе укажите цифру выбранного варианта.
1) log 3 5 ;
2) log 1
1
3
7
4) log1,5 .
;
3) log 0,6 ;
3
4
9 4
38. Выберите наименьшее число из трёх данных. В ответе укажите цифру выбранного варианта.
8
1) log 0,5 11 ;
2) log 1
а) 1) log 5 4;
2) log 0,5 5;
3) log 25 3 ;
б) 1) log 6 5;
2) log 0,6 6;
3) log 36 4 .
39. Найдите значения выражений:
а) log
19
19 ;
б) log 7 74 ;
г) log 63 618 ;
д) log 3
1
9 3
в) log 54 5 ;
;
е) log17
1
.
17 17
40. Найдите значения выражений:
а) log 7 ( log 2 128 ) ;
(
б) log 6 ( log 3 729 ) ;
)
( log 4 64 ) .
в) log 2 log 5 5 ;
г) log
в) log 4 3, 2 + log 4 20 ;
г) log 2 0, 25 + log 2 128 .
3
41. Найдите значения выражений:
б) log 2 40 + log 2 0,8 ;
а) log 6 9 + log 6 24
42. Найдите значения выражений:
б) log 2 108 − log 2 27 ;
а) log 3 54 − log 3 2 ;
в) log 7 294 − log 7 6 ;
г) lg 0,04 − lg 0, 4 .
43. Найдите значения выражений:
а)
log 5 136
2log 5 13
б)
3log19 98
log 21 1715
; в)
;
3log 21 17
log19 96
г)
log 23 144
.
4log 23 12
44. Найдите значения выражений:
а) 7log1/ 7 25 ;
б) 104lg 3 ;
в) e3ln 4 ;
г) 2log8 27 ;
е) 7 2 − log7 49 ;
ж) 25log5 9 ;
з) 343log7 5 ;
и) 5log2 3
(
)
д) 31+ log3 11 ;
log5 2
(
к) 11log7 13
;
)
log11 7
.
45. Найдите значения выражений:
а) log11 3 ⋅ log 3 11 ;
б) log16 10 ⋅ log10 32 ;
в) 9 ⋅ log 3 2 ⋅ log8 3 ;
г) log 4 3 ⋅ log 3 16 .
46. Найдите значения выражений:
1
;
12
в) log a b18 a , если log b a = 6 ;
а) log b 4 a , если log a b =
(
)
б) log
6
a
1
6
, если log a b = 2 .
b , если log b a = ;
г) log b ( a 5b9 )
Проверочная работа № 4
Вариант 1
Найдите значения выражений:
1. а) log 7 343 ;
б) log 5 0,04 ;
в) log 23 1;
г) log 2 5 4 ;
2. а) log15 5 + log15 45 ; б) log8 136 − log8 17 ; в)
9
7 log 6 15
;
3log 6 15
д) log 25 ( log 3 243) .
г) 53+ log5 2 ;
д) 8 ⋅ log 9 2 ⋅ log 2 81 .
Вариант 2
Найдите значения выражений:
1. а) log 9 729 ;
б) log 2 0,125 ;
в) log 32 1;
2. а) log 6 108 + log 6 2 ; б) log 4 768 − log 4 3 ; в)
г) log 9 4 3 ;
log8 127
;
14log8 12
д) log 9 ( log8 512 ) .
г) 32log2 3 ; д) 12 ⋅ log16 7 ⋅ log 7 32 .
9
1.5. Тригонометрические выражения
47. Найдите значения выражений:
а)
3 sin 240° ;
б) −2 2 sin 405° ;
в) 8sin 750° ;
г) 5 3 sin(−540)° ;
д) −3 2 cos 675° ; е) 7 3 cos150° ;
ж) −12cos 480° ;
з) 13cos(−720)° ;
и) 29 tg 900° ;
л)
3
tg 315° ;
2
м) −10 3 tg 600° .
к) 8 3 tg (−240)° ;
48. Найдите значения выражений:
а)
15sin 70°
;
cos 20°
б)
cos 40°
;
4sin 50°
в)
−3sin 217°
;
sin 37°
г) −
cos 46°
.
8cos 406°
49. Найдите значения выражений:
а) −6 tg 24° tg 66° ;
б) −2 tg15° tg 75° ;
в)
−151tg 29°
;
tg151°
г)
25 tg175°
.
tg 5°
3π
50. Найдите sin α , если cos α =0,8 и α ∈ ; 2π .
2
1
π
51. Найдите 10 sin α , если cos α = −
и α ∈ ; π .
10
2
5π
52. Найдите cos α , если sin α = −0,96 и α ∈ −3π; − .
2
2
π
53. Найдите −2 13 cos α , если sin α = −
и α ∈ −π; − .
2
13
1
5π
и α ∈ −3π; − .
54. Найдите tg α , если cos α = −
2
26
π
55. Найдите tg α , если sin α = −0,6 и α ∈ − ; 0 .
2
Проверочная работа № 5
Вариант 1
Найдите значения выражений:
1. а) −6 2 cos 405° ;
2. Найдите
б) 15sin(−900)° ;
5 cos α , если sin α = −
в) −3 3 tg120° ;
г)
−3cos18°
;
sin 72°
д)
21tg 201°
.
tg 21°
1
3π
и α ∈ π; .
5
2
Вариант 2
Найдите значения выражений:
1. а) −8 3 cos(−330)° ;
10
б) 16sin 570° ;
в) 12 tg (−225)° ;
2. Найдите − 29 sin α , если cos α = −
2
π
и α ∈ ; π .
29
2
г)
cos 233°
;
8cos53°
д) −13tg 28° tg 62° .
1.6. Координатная прямая
56. На координатной прямой точками A, B, C и D отмечены числа. Установите соответствие между
указанными точками и числами из правого столбца, которые им соответствуют.
A
B C
D
ТОЧКИ
А) А
Б) B
В) C
Г) D
ЧИСЛА
1) 0,07
6
83
3) −0,972
2) −
4)
25
27
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
57. На координатной прямой точками A, B, C и D отмечены числа. Установите соответствие между
указанными точками и числами из правого столбца, которые им соответствуют.
A B
C
ТОЧКИ
ЧИСЛА
А) А
Б) B
В) C
Г) D
1) –2,7
2)
D
83
39
3) 3,2
4) −
51
16
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
11
58. На координатной прямой точками A, B, C и D отмечены числа. Установите соответствие между
указанными точками и числами из правого столбца, которые им соответствуют.
A
B
C
D
ТОЧКИ
ЧИСЛА
А) А
Б) B
В) C
Г) D
1) 1,8
66
23
3) – 0,73
38
4) −
15
2)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
59. На координатной прямой точками A, B, C и D отмечены числа.Установите соответствие между
указанными точками и числами из правого столбца, которые им соответствуют.
A
B
C
D
ТОЧКИ
ЧИСЛА
А) А
Б) B
В) C
Г) D
1) – 3,993
79
44
3) 3,37
51
4) −
29
2)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
60. На координатной прямой точками A, B, C и D отмечены числа. Установите соответствие между
указанными точками и числами из правого столбца, которые им соответствуют.
A
0
12
1
B
2
C
3
4
D
5
6
x
ТОЧКИ
ЧИСЛА
А) А
Б) B
В) C
Г) D
1)
23
2)
1, 4
3)
7
4)
34
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
61. На координатной прямой точками A, B, C и D отмечены числа. Установите соответствие между
указанными точками и числами из правого столбца, которые им соответствуют.
ТОЧКИ
ЧИСЛА
А) А
Б) B
В) C
Г) D
1)
38
2)
47
3)
62
4)
53
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
62. На прямой отмечены точки K, L, M, N. Установите соответствие между указанными точками и
числами из правого столбца, которые им соответствуют.
KL
1
2
M
3
4
5
ТОЧКИ
А) K
Б) L
В) M
Г) N
N
6
7
8
ЧИСЛА
1)
13 + 3
2)
13 ⋅ 3
3)
13 − 3
4)
( 3)
3
−3
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
13
63. На прямой отмечены точки A, B, C, D. Установите соответствие между указанными точками и
числами из правого столбца, которые им соответствуют.
A B
C
1
2
3
4
5
ТОЧКИ
А) A
Б) B
В) C
Г) D
D
6
7
8
ЧИСЛА
1)
11 − 5
2)
5 : 11
3)
11 + 5
4)
( 5)
3
− 11
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
64. Число a равно 0,7 . Установите соответствие между числами из левого столбца и отрезками,
которым они принадлежат из правого столбца.
ЧИСЛА
ОТРЕЗОК
А) − a − 1
Б) a
2
4+a
В)
Г)
5
a
1) [ −2; −1]
2) [ 0;1]
3) [ 2;3]
4) [5;6]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
65. Число a равно 3,1 . Известно, что точки A, B, C, D на координатной прямой соответствуют
числам и расположены в порядке их возрастания. Установите соответствие между указанными
точками и числами из правого столбца, которые им соответствуют.
A
BC
ТОЧКИ
А) А
Б) B
В) C
Г) D
ЧИСЛА
1) 4 − a
5
2) −
a
3)
a+4
4) a
2
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
14
А
Б
В
Г
D
66. На координатной прямой отмечены точки A, B, C, D. Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
A
0
B
1
2
C
D
3
4
5
ТОЧКИ
ЧИСЛА
А) А
Б) B
В) C
Г) D
1) log 4 3
x
6
37
9
3) 3,8
2)
−1
4
4)
13
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
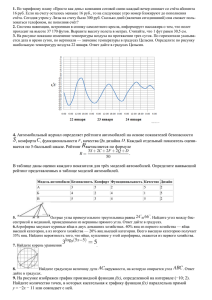
67. На координатной прямой отмечены точки A, B, C, D. Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
A
B
C
ТОЧКИ
ЧИСЛА
А) А
Б) B
В) C
Г) D
1) 3, 2
2) 0,61
D
3) log 3 11
16
4) −
15
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
68. На координатной прямой отмечены точки K, L, M, N. Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
ТОЧКИ
А) K
Б) L
В) M
Г) N
ЧИСЛА
1) log 3 40
16
7
3) 27
2)
4) 0,7 −1
15
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
69. На координатной прямой отмечено число a, а также точки K, L, M, N. Установите соответствие
между указанными точками и числами из правого столбца, которые им соответствуют.
K m
a
–1
0
1
L
2
ТОЧКИ
M
3
N
4
5
x
ЧИСЛА
А) K
Б) L
В) M
Г) N
1) a
2) a + 4,3
3) a 2
5,7
4)
a
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
70. На координатной прямой отмечены точки A, B, C, D. Число a равно log 5 11 . Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
A
B
–1
0
C
1
D
2
3
ТОЧКИ
ЧИСЛА
А) А
Б) B
В) C
Г) D
1) 6,1 − a
4
5
2) a 2
2,1
3) −
a
4) a − 1,1
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
71. На координатной прямой отмечено число a.
m
a
–1
0
1
2
Установите соответствие между числами из левого столбца и отрезками из правого столбца,
которым эти точки принадлежат.
16
ЧИСЛА
ОТРЕЗКИ
А) 4a
0,2
Б)
a
1) [ −3; −2]
2) [ 0;1]
3) [1;2]
В) a + 2
Г) a − 3
4) [3;4]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
72. На координатной прямой отмечены числа a и b.
an
–3
–2
–1
0
1
b
m
2
3
x
Установите соответствие между числами из левого столбца и отрезками из правого столбца,
которым эти точки принадлежат.
ЧИСЛА
ОТРЕЗКИ
А) ab
Б) a + b
a
В)
b
1
Г) + ba
ba
1) [ 0;1]
2) [1;2]
3) [ 2;3]
4) [3;4]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
1.7. Числа и их свойства
73. Найдите двузначное число, которое на 3 больше суммы квадратов цифр, составляющих его, и больше
удвоенного произведения этих же цифр на 7. В ответе запишите какое-нибудь одно такое число.
74. Сумма цифр двузначного числа равна 9. Если к этому числу прибавить 45, то получится число,
записанное теми же цифрами, но в обратном порядке. Найдите исходное число.
75. Результат деления двузначного числа на произведение его цифр равен 3. Найдите одно какоенибудь такое число.
76. Если двузначное число разделить на сумму его цифр, то получится в частном 4, а в остатке 3.
Найдите исходное число.
77. Трёхзначное число, первая цифра которого 5, разделили на сумму квадратов его цифр. Получили 14. Найдите исходное число.
78. Трёхзначное число, первая цифра которого 9, разделили на сумму квадратов его цифр. В остатке
получили 0. Найдите исходное число. В ответ запишите какое-нибудь одно такое число.
79. Если к трёхзначному натуральному числу прибавить 396, то получится исходное число, записанное в обратном порядке. Найдите исходное число, если оно лежит в диапазоне от 300 до 350. В
ответ запишите какое-нибудь одно такое число.
17
80. Если к трёхзначному натуральному числу прибавить 99, то получится исходное число, записанное
в обратном порядке. Найдите исходное число, если оно лежит в диапазоне от 100 до 150. В ответ
запишите какое-нибудь одно такое число.
81. В четырёхзначном числе все цифры различны и оно не превосходит 1100. Исходное число записали в обратном порядке. Из получившегося числа вычли исходное число. Затем, из получившегося
результата извлекли корень. Получили 66. Найдите исходное число.
82. В четырёхзначном числе все цифры различны и оно не превосходит 1100. Исходное число записали в обратном порядке. Из получившегося числа вычли исходное число. Затем, из получившегося
результата извлекли корень. Получили 75. Найдите исходное число.
83. В четырёхзначном числе все цифры различны. Деление числа на 3 даёт остаток 1. Деление числа на 5 даёт остаток 2. Деление числа на 7 даёт остаток 3. Деление числа на 11 даёт остаток 4.
Найдите исходное число. В ответ запишите какое-нибудь одно такое число.
84. В четырёхзначном числе все цифры различны. Деление числа на числа 3, 5, 7, 11 даёт одинаковые
остатки, равные 1. Найдите исходное число. В ответ запишите какое-нибудь одно такое число.
85. Найдите четырёхзначное число, кратное 25, такое что произведение его цифр больше 15, но
меньше 30. В ответ запишите какое-нибудь одно такое число.
86. Найдите трёхзначное натуральное число, не кратное 10, которое при делении на 3 и на 7 даёт
одинаковые остатки, отличные от нуля, а его вторая цифра является средним арифметическим
первой и последней цифры. В ответ запишите какое-нибудь одно такое число.
87. Найдите трёхзначное натуральное число, не кратное 10, которое при делении на 7 и на 11 даёт
одинаковые остатки, отличные от нуля, а его вторая цифра является средним арифметическим
первой и последней цифры. В ответ запишите какое-нибудь одно такое число.
88. Найдите четырёхзначное число, не превосходящее 3000, состоящее только из четных цифр и
все цифры которого различны, такое что сумма первых двух цифр, равна сумме двух последних
цифр. В ответ запишите какое-нибудь одно такое число.
89. Найдите четырёхзначное число, не превосходящее 5000, кратное первым пяти простым числам
(2, 3, 5, 7, 11). В ответ запишите какое-нибудь одно такое число.
90. Найдите четырёхзначное число, большее 8000, в котором все цифры различны, кратное 2, 3, 5 и
7. В ответ запишите какое-нибудь одно такое число.
91. Вычеркните в числе 91462574 три цифры так, чтобы получившееся число делилось на 18. В ответ запишите какое-нибудь одно получившееся число.
92. Вычеркните в числе 35614792 три цифры так, чтобы получившееся число делилось на 24. В ответ запишите какое-нибудь одно получившееся число.
Проверочная работа № 6
Вариант 1
1. Дано трёхзначное число, меньшее 900, все цифры которого различны. Деление числа на
11 даёт остаток 2. Деление числа на 13 даёт остаток 1. Найдите исходное число.
2.
Найдите пятизначное число, кратное 11, запись которого содержит только цифры 1 и 2, такое что произведение его цифр равно сумме его цифр. В ответ запишите какое-нибудь одно
такое число.
18
Вариант 2
1.
Дано трёхзначное число, большее 900, все цифры которого различны. При делении числа
как на 13, так и на 15 в остатке получается 1. Найдите исходное число.
2.
Найдите пятизначное число, кратное 8, запись которого содержит только цифры 1 и 4, такое
что произведение его цифр на 49 больше суммы его цифр. В ответ запишите какое-нибудь
одно такое число.
§ 2. Уравнения
93. Решите уравнения:
а) 5 x + 13 = 2 x − 5 ;
б) 10 x − 14 = 2 x + 18 ;
в) −3 x − 17 =1 − 9 x ;
г) −4 x + 23 =−4 − 13 x .
94. Решите уравнения:
x x
x 3
+ x;
б) 2 + = ;
а) =
8 16
4 2
95. Решите уравнения:
в)
x
x
x
x
− 5 =− ; б) = 15 − ;
12
18
14
21
96. Решите уравнения:
а)
x
3
2x
1
=2 ;
=3 ;
б)
11
11
13
13
97. Решите уравнения:
г)
x
x
= 4− .
30
6
x
x
=;
15 12
г)
x
x
=−7 +
.
20
25
в) 3 −
в)
а)
x
x
= 8− ;
21
7
3x
5
= −2 ;
14
14
г) −
а) 7 x − 3( x + 4) = 22 − 6 x ;
−7 x + 30 ;
б) 6 x − 5( x + 2) =
в) 8 x − 9(3 − 2 x) = 10 x − 11 ;
г) 4 x − 6(5 − 7 x) =6 x + 20 .
11x
1
=
3 .
18
18
98. Решите уравнения:
x −1
x+2
=−1 +
;
6
4
6+ x
x−4
+2=
в)
;
10
15
99. Решите уравнения:
а)
x−3 4− x
=;
4
5
3− x
x+5
= 7−
г)
.
12
20
б) 5 −
а) ( x + 5) 2 =(3 + x) 2 ;
б) ( x − 7) 2 =(2 − x) 2 ;
в) (2 x − 1) 2 =(3 − 2 x) 2 ;
г) (2 − 4 x) 2 =(4 x − 3) 2 .
100. Решите уравнения:
0 ; б) 25 x 2 − 9 =
0;
а) 49 − 16 x 2 =
в) −1 + 4 x 2 =0 ;
г) −8 + 128 x 2 =0 .
101. Решите уравнения:
20 ;
а) ( x − 3) 2 + (3 x + 1) 2 =
104 ;
б) (5 x − 2) 2 + ( x + 10) 2 =
в) (6 − x) 2 = (3 x − 2) 2 − 40 ;
г) (10 − 3 x) 2 =(5 x − 6) 2 .
19
102. Решите уравнения:
0;
0;
б) 104 x − 13 x 2 =
а) 84 x − 6 x 2 =
0;
в) 62 x + x 2 =
0.
г) 36 x + 4 x =
в) 18x = x 2 ;
г) 25x = − x 2 .
103. Решите уравнения:
а) 19 x 2 = 57 x ;
б) 21x 2 = −63 x ;
104. Решите уравнения:
8 0,3x 2 + 8 ;
а) 0,12 x +=
= 0, 2 x 2 + 15 ;
б) 1,8 x + 15
7 − 0,02 x 2 ;
в) 7 − 0,03 x =
г) 34 + 0, 4 x 2 = 0,05 x + 34 .
105. Решите уравнения:
а) (2 x − 5) 2 =( x + 5) 2 ;
0;
б) ( x − 6) 2 − (2 x + 6) 2 =
в) (10 − 3 x) 2 =(5 x − 10) 2 ;
0.
г) (7 − x) 2 − (3 x − 7) 2 =
106. Решите уравнения:
0;
а) x 2 + 8 x + 16 =
0;
б) 4 x 2 + 4 x + 1 =
0;
в) x 2 − 12 x + 36 =
0.
г) 25 x 2 − 10 x + 1 =
0;
б) x 2 + 7 x + 6 =
0;
в) x 2 − x − 6 =
0.
г) x 2 + x − 6 =
0;
б) x 2 + 8 x + 15 =
0;
в) x 2 − 14 x + 48 =
0.
г) x 2 + 11x + 24 =
0;
а) −2 x − 5 x 2 + 3 =
0;
б) 11x − 5 x 2 − 2 =
0;
в) 3 + x − 4 x 2 =
0;
г) 9 − 8 x − x 2 =
0;
д) 3 x − 54 + x 2 =
0;
е) 4 − 8 x − 5 x 2 =
ж) 15 x + 13 + 2 x 2 =
0;
з) 3 − 14 x − 5 x 2 =
0.
107. Решите уравнения:
0;
а) x 2 − 7 x + 6 =
108. Решите уравнения:
0;
а) x 2 − 10 x + 16 =
109. Решите уравнения:
110. Решите уравнения:
а) 2 x 2 − 13 x + 5 = x 2 − 3 x − 4 ;
б) 5 x 2 + 3 x − 16 = 7 x 2 − 2 x − 14 ;
в) 10 x 2 + 6 x − 11 = 9 x 2 + 21x + 5 ;
5 12 x 2 − 5 x − 26 .
г) 2 x 2 − 6 x −=
111. Решите уравнения:
а) 2 x 2 + 17 x + 27 = ( x + 3) 2 ;
б) (2 x − 3) 2 = 3x 2 − 10 x + 24 ;
в) 7 x 2 − 16 x + 10 = (2 − 3 x) 2 ;
г) (7 − 5 x) 2 = 23 x 2 − 59 x + 37 .
112. Решите уравнения:
0;
а) (3 − x)(4 x − 3) =
0.
б) (5 x + 1)(14 − 2 x) =
0;
в) (8 + 16 x)(5 x − 15) =
0.
г) (6 x − 12)(8 x + 5) =
113. Решите уравнения:
а)
20
9
= 3;
x−2
б) 5 =
2
;
3− x
в)
11
= −4 ;
x+3
г) 10 =
13
.
7−x
114. Решите уравнения:
а)
12
12
=
;
2 x − 3 23
б)
35
35
= ;
18 − x 43
в)
47
47
=
;
2 − 17 x 53
3− x
=4;
x+5
1+ x
в) −3 =
;
x − 10
г)
29
29
= .
36 − 3 x 45
115. Решите уравнения:
а)
x−5
=2;
x −8
б)
x − 11
г) −2 =
.
6− x
116. Решите уравнения:
а)
1
1
2
1
+
=
0;
−
=
0;
б)
x−2 x−3
x+7 x+5
в)
3
2
−
=
0;
x−6 x+9
г)
5
4
−
=
0.
x −1 x + 8
117. Решите уравнения:
а)
2x − 5 =
1;
б)
д)
1 1
= ;
x 5
е)
4 − 3x =
5;
1
1
= ;
x 13
118. Решите уравнения:
а) 2 x = 1 ;
3− x
г) 81
1
=
;
27
1
в)
9
б) 53 x−3 = 125 ;
1
д)
7
− x+2
x+7 −3=
0;
г)
12 − x − 5 =
0;
ж)
2 1
− =
0;
x 3
з)
3
3
− =
0.
x 14
x− 2
1
е)
10
= 343 ;
в)
= 3;
6 x −5
= 0,01x .
119. Решите уравнения:
1
а) 45− x ⋅ 43 x − 2 =;
256
б) 2− x + 7 : 22 x +1 = 64 ;
64 ;
в) 85 x − 2 ⋅ 512− x +1 =
1.
г) 0, 25 x + 3 : 4 x =
б) log 5 x = −3 ;
−2 ;
в) log 2 ( x + 0,75) =
2.
г) log 6 ( x − 4) =
120. Решите уравнения:
а) log 3 x = 4 ;
121. Решите уравнения:
+ 3) log12 (6 x + 7) ;
а) log12 (8 x=
− 3) log17 (3x + 4) ;
б) log17 (5 x=
log 2 3 ;
в) log 2 ( x − 3) + log 2 5 =
log 4 10 .
г) log 4 (3 x + 12) − log 4 3 =
122. Решите уравнения:
− 5) log 2 (2 x + 8) − 1 ;
а) log 2 (3 x =
log 2 ( x − 5) + 1 ;
б) log=
2 x
3;
в) log 3 x + log 3 ( x − 6) =
1.
г) log 6 (2 x) − log 6 (3 x − 8) =
21
Проверочная работа № 7
Вариант 1
1. Решите уравнения:
2x
3
1 5x − 1 5 − x
= 3 ; в) −
=; г) (7 − x) 2 =( x + 3) 2 .
17
17
4
8
6
2. Решите уравнения и выполните указание:
а) 2(6 − 2 x) − 4 = 18 − 3(1 + 3 x) ; б)
0 . Если уравнение имеет более одного корня, то в ответе укажите меньший из них.
а) 36 − 144 x 2 =
б) 5 x 2 = −45 x . Если уравнение имеет более одного корня, то в ответе укажите сумму корней.
0 . Если уравнение имеет более одного корня, то в ответе укажите больший из них
в) (8 x − 2)(10 x + 15) =
0 . Если уравнение имеет более одного корня, то в ответе укажите меньший из них.
г) x 2 − 16 x + 64 =
0 . Если уравнение имеет более одного корня, то в ответе укажите больший из них.
д) x 2 − x − 20 =
0 . Если уравнение имеет более одного корня, то в ответе укажите меньший из них.
е) 13 x + 3 x 2 − 10 =
ж) (4 x − 5) 2 = 14 x 2 − 47 x + 34 Если уравнение имеет более одного корня, то в ответе укажите произведение корней.
3. Решите уравнения:
35
18 + 2 x
; б) 7 =
;
а) 7 =
x−4
9− x
4. Решите уравнения:
а) 4 x−5 = 8 ;
в)
1
б) 32 − x ⋅ 32 x + 4 =
;
27
1
2
−
=
0 ; г)
4− x 7− x
в) log 4 x = −1 ;
6 + 4x =
4.
log 5 ( x − 3) + 2 .
г) log=
5 x
Вариант 2
1. Решите уравнения:
x
x
1 4+ x 9− x
= ; в) −
=;
18 27
5
6
12
2. Решите уравнения и выполните указание:
−7(9 − 5 x) ; б) 5 −
а) 22 − 5(2 + 3 x) =
г) ( x + 4) 2 =(6 − x) 2 .
0 . Если уравнение имеет более одного корня, то в ответе укажите меньший из них.
а) −25 + 100 x 2 =
8 x 2 . Если уравнение имеет более одного корня, то в ответе укажите сумму корней.
б) −56 x =
0 . Если уравнение имеет более одного корня, то в ответе укажите больший
в) (9 x + 18)(8 x − 6) =
из них.
0 . Если уравнение имеет более одного корня, то в ответе укажите меньший из них.
г) x 2 − 14 x + 49 =
0 . Если уравнение имеет более одного корня, то в ответе укажите больший из них.
д) x 2 + 11x + 18 =
0 . Если уравнение имеет более одного корня, то в ответе укажите больший из них.
е) 2 + 7 x 2 − 9 x =
ж) (5 x + 7) 2 = 17 x 2 + 84 x + 46 Если уравнение имеет более одного корня, то в ответе укажите произведение корней.
3. Решите уравнения:
24
45( x − 1)
=8;
= 15 ;
б)
а)
11 − x
5− x
4. Решите уравнения:
а) 625 x+8 = 25 ;
.
22
б) 23+ x : 2−3 x + 5 =
в)
1
;
16
2
1
−
=
0 ; г)
5− x 6− x
в) log11 x = 2 ;
5 − 2x =
3.
= log 4 x − 2 .
г) log 4 ( x − 3)
§ 3. Неравенства
123. Решите неравенства:
а) ( x − 7)(2 − x) ≤ 0 ;
б) ( x − 3)( x + 2) < 0 ;
в) (18 − 3 x)( x − 7) ≥ 0 ;
г) (4 x − 12)(9 + x) > 0 .
124. Решите неравенства:
а) x 2 − 10 x + 21 ≥ 0 ;
б) 3 x 2 + x − 4 < 0 ;
в) 2 x 2 + x − 3 ≤ 0 ;
г) x 2 − 2 x − 35 > 0 ;
д) 9 x 2 − 8 x − 1 ≤ 0 ;
е) x 2 − 3 x + 13 < 0 ;
ж) −7 x 2 + 9 x + 10 < 0 ;
з) − x 2 + 5 x − 24 < 0 ;
и) −7 x 2 + 18 x + 9 ≥ 0 ;
к) 2 x 2 − 6 x + 9 < 0 ;
л) −4 x 2 + 3 x + 1 < 0 ;
м) 3 x 2 − 7 x − 8 ≥ 0 .
125. Решите неравенства:
а)
x
≤0;
x−2
б)
3− x
≥0;
x+4
в)
x+7
≥0;
x−5
г)
11 − x
<0;
14 − 2 x
д)
x+3
>0;
12 − x
е)
13 − x
<0;
3 x + 27
ж)
2 x + 30
≤0;
14 − x
з)
18 − x
≥0.
2x
126. Решите неравенства:
а) ( x − 1) 2 ( x + 3) > 0 ;
д)
x
≤0;
( x − 2) 2
и)
( x + 3) 2
>0;
(12 − x)3
б) ( x − 5)( x − 3) 2 ≤ 0 ;
(3 − x) 2
≥ 0;
x+4
е)
к)
ж)
в) ( x − 7) 2 ( x − 6)3 ≥ 0 ;
x+7
≥0;
( x − 5) 2
з)
г) x 2 ( x + 2)3 > 0 ;
(11 − x)3
<0;
(14 − 2 x) 2
x2
<0.
( x + 2)3
127. Решите неравенства:
x
x
а) 2 > 2 ;
б) 3x+1 ≤ 3 ;
в) 0,5 ≥ 0,5 ;
1
1
г) >
;
3 81
д) 52 − x ≤ 25 ;
е) 9 x− 4 ≥ 27 ;
ж) 0,8 x ≥ 1, 25 ;
з)
−x
1
7
2 x+ 3
<
1
.
49
128. Решите неравенства:
а) log 2 x > 2 ;
б) log 3 x ≤ 1 ;
в) log 2 x ≥ −1 ;
г) log 4 x < 2 ;
д) log 2 ( x + 3) ≤ 1 ;
е) log 5 ( x − 4) ≥ −1 ;
ж) log 7 x ≥ 0 ;
з) log8 (3 − x) < 0 ;
и) log 0,2 x > 0 ;
к) log 0,7 x < 0 ;
л) log 0,1 ( x + 1) ≥ 2 ;
м) log 0,3 ( x − 2) ≤ 1 .
23
129. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А)
x−9
<0
x−6
РЕШЕНИЯ
1) ( 6;9 ) (9; +∞ )
Б) ( x − 9) 2 ( x − 6) < 0
2) ( −∞;6 ) ( 9; +∞ )
В) ( x − 6)( x − 9) > 0
3) ( −∞;6 )
Г)
2
( x − 9)
>0
x−6
4) ( 6;9 )
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
130. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А) ( x − 3) 2 ( x − 7) < 0
1) ( −∞;3) (3;7)
Б) ( x − 3)( x − 7) < 0
2) (3;7)
x−3
>0
x−7
( x − 7) 2
>0
Г)
x−3
3) ( 3;7 ) ( 7;+∞ )
В)
4) ( −∞;3) ( 7; +∞ )
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
131. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А) x 2 − 9 x + 18 ≥ 0
2
Б) x − 7 x − 18 ≤ 0
2
В) x + 9 x + 18 ≥ 0
2
Г) x + 7 x − 18 ≤ 0
В таблице под каждой буквой укажите
Ответ:
24
А
Б
В
Г
1)
РЕШЕНИЯ
1)
–9
1)
–9
1)
–9
2)
–9
2)
–6
2)
–6
2)
–6
3)
–6
3)
–2
3)
–2
3)
–2
4)
–2
4)
3
4)
3
4)
3
соответствующий
номер.
3
2
2
2
–32
–3
–3
–3
9
9
9
9
6
6
6
6
x
x
x
xx
x
x
x
x
x
x
xx
x
x
x
132. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
В таблице под
Ответ:
А
1)
РЕШЕНИЯ
1)
1)
1)
2)
2)
2)
2)
3)
3)
3)
3)
4)
4)
4)
4)
3
3
2
3
x
+
7
x
+
12
≥
0
А)
3
–1
–1
2
Б) x − 7 x + 12 ≥ 0
–1
–1
2
–4
В) x − 11x − 12 ≤ 0
–4
–4
–4
Г) x 2 + 11x − 12 ≤ 0
–12
–12
–12
–12
каждой буквой укажите соответствующий
Б
В
номер.
4
4
4
4
12
12
12
12
–3
–3
–3
–3
1
1
1
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Г
133. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А) 5 x−1 > 5
1) ( −∞; −2 )
Б) 0, 2 x > 0,04
2) ( −∞;2 )
В) 5− x < 25
3) ( 2;+∞ )
Г) 0, 2 < 0,04
−x
4)
( −2; +∞ )
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
134. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А) 3x− 2 > 3
1) ( −3; +∞ )
1
3
x
Б) >
1
27
В) 3− x < 27
1
Г)
3
−x
<
1
27
2) ( −∞;3)
3) ( −∞; − 3)
4) ( 3;+∞ )
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
25
135. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А)
Б)
В)
Г)
РЕШЕНИЯ
log 4 x > 1
log 4 x < −1
log 4 x < 1
log 4 x > −1
1)
2)
3)
4)
( 0, 25;+∞ )
( 4;+∞ )
( 0;4 )
( 0;0, 25)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
136. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А) log 5 x ≥ 2
1) ( 0; 25]
Б) log 5 x ≤ −2
2) [ 25; + ∞ )
В) log 5 x ≤ 2
3) [ 0,04; + ∞ )
Г) log 5 x ≥ −2
4) ( 0; 0,04]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
Проверочная работа № 8
Вариант 1
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А)
x+3
<0
( x − 4) 2
Б) 4 x > 64
В) log 4 ( x + 1) < 1
Г) x 2 − 3 x > 0
1)
1)
РЕШЕНИЯ
0
0
1)
1)
0
2)
0
2)
2)
2)
3)
3)
3)
3)
4)
4)
–1
–1
4)
4)
–1
–1
–3
–3
–3
–3
3
3
3
3
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
26
А
Б
В
Г
3
3
3
3
3
3
3
3
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Вариант 2
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А) ( x − 4) 2 ( x − 5) < 0
Б) log 5 ( x − 4) < 0
В) x 2 − 9 x + 20 > 0
Г) 4 x− 2 > 16
1)
РЕШЕНИЯ
1)
4
1)
4
1)
4
2)
4
2)
4
2)
4
2)
4
3)
3)
44
3)
4
3)
4
4)
44
4)
4)
4
4)
4
4
5
5
5
55
5
5
5
5
5
5
5
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
x
x
x
xx
x
x
xx
x
x
xx
x
x
x
Г
§ 4. Текстовые задачи
4.1. Размеры и единицы измерения
137. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) ширина стола
Б) высота потолка в квартире
В) высота Останкинской телебашни
Г) длина реки Волга
1)
2)
3)
4)
540 м
3м
3530 км
50 см
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
138. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) ширина окна
Б) высота столба
В) высота Спасской башни Кремля
Г) длина реки Нева
1)
2)
3)
4)
120 см
74 км
420 см
71 м
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
27
139. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) длина реки Лена
Б) длина беговой дорожки на стадионе
В) высота 14-этажного дома
Г) высота горы Эльбрус
1)
2)
3)
4)
400 м
4294 км
42 м
5642 м
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
140. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) расстояние от Земли до Луны
Б) расстояние от Москвы до Санкт-Петербурга
В) длина футбольного поля
Г) радиус Земли
1)
2)
3)
4)
700 км
384000 км
6400 км
105 м
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
141. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) толщина листа бумаги
Б) рост жирафа
В) длина пальца на руке
Г) высота небоскреба
1)
2)
3)
4)
250 м
8 см
6м
0,1 мм
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
142. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) время оборота Земли вокруг Солнца
Б) длительность учебного занятия в университете
В) длительность авиаперелета Москва-Владивосток
Г) длительность затухания звука хлопка ладоней
28
ЗНАЧЕНИЯ
1) 90 минут
2) 0,015 секунды
3) 365 суток
4) 8 часов
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
143. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ЗНАЧЕНИЯ
ВЕЛИЧИНЫ
А) масса золотого кольца
1) 500 г
2) 75 кг
Б) масса льва
В) масса волейбольного мяча
3) 5 г
4) 1,5 ц
Г) масса человека
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
144. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ЗНАЧЕНИЯ
ВЕЛИЧИНЫ
А) масса деревянного дома
1) 800 ц
Б) масса мешка цемента
2) 50 кг
3) 1 кг
В) масса бутылки воды
Г) масса акулы
4) 16 т
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
145. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ЗНАЧЕНИЯ
ВЕЛИЧИНЫ
А) объём воды в Телецком озере
1) 50 л
Б) объём кастрюли
2) 170 л
В) объём ванны
3) 5 л
Г) объём кофра для хранения
4) 40 км3
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
146. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) объём шкафа
1) 0,3 л
Б) объём воды в Чёрном море
2) 27 м3
В) объём банки сгущённого молока
3) 2,5 м3
Г) объём бассейна
4) 555 тыс. км3
29
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
147. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ЗНАЧЕНИЯ
ВЕЛИЧИНЫ
А) площадь визитной карточки
1) 108 см2
Б) площадь стены на кухне
2) 7100 м2
В) площадь фермерского поля
3) 4500 мм2
Г) площадь фотографии
4) 15 м2
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
148. Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ЗНАЧЕНИЯ
ВЕЛИЧИНЫ
А) площадь листа А4
1) 3,3 млн км2
Б) площадь окна
2) 830 м2
В) площадь дачного участка
3) 18788 см2
Г) площадь Индии
4) 62370 мм2
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
149. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ЗНАЧЕНИЯ
ВЕЛИЧИНЫ
А) скорость пешехода
1) 330 м/c
Б) скорость мотоциклиста
2) 300000 км/c
В) скорость звука
3) 5 км/ч
Г) скорость света
4) 90 км/ч
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
150. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
1) 1 об/год
А) частота обращения Земли вокруг Солнца
Б) частота обращения минутной стрелки
2) 1 об/сутки
В) частота обращения Земли вокруг своей оси
3) 1 об/час
Г) частота обращения секундной стрелки
4) 1 об/минуту
30
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
4.2. Формулы
151. а) Используя закон Гука в виде F = kx , где F – сила (в ньютонах), с которой растягивают пружину,
x – абсолютное удлинение пружины (в метрах), а k – коэффициент упругости (в Н/м), найдите
х (в метрах), если F = 62 Н и k = 2 Н/м.
б) Используя закон Гука в виде F = kx , где F – сила (в ньютонах), с которой растягивают пружину,
x – абсолютное удлинение пружины (в метрах), а k – коэффициент упругости (в Н/м), найдите
F (в ньютонах), если x = 2 м и k = 230 Н/м.
5
( tF − 32 ) ,
9
где tC – температура в градусах по шкале Цельсия, t F – температура в градусах по шкале
Фаренгейта, найдите, скольким градусам по шкале Цельсия соответствует 131 градус по шкале
Фаренгейта?
152. а) Используя формулу перевода температуры из шкалы Цельсия в шкалу Фаренгейта=
tC
б) Используя формулу перевода температуры из шкалы Цельсия в шкалу Фаренгейта
5
=
tC
( tF − 32 ) , где tC – температура в градусах по шкале Цельсия, tF – температура в градусах по
9
шкале Фаренгейта, найдите, скольким градусам по шкале Фаренгейта соответствует 15 градусов
по шкале Цельсия?
153. а) Используя второй закон Ньютона в виде F = ma , где F – сила (в ньютонах), действующая
на тело, m – его масса (в килограммах), а – ускорение тела (в м/c2), найдите а (в м/c2), если
F = 150 Н и m = 75 кг.
б) Используя второй закон Ньютона в виде F = ma , где F – сила (в ньютонах), действующая на
тело, m – его масса (в килограммах), а – ускорение тела (в м/c2), найдите F (в ньютонах), если
a = 15 м/c2 и m = 75 кг.
mv 2
, где m – масса
2
тела (в килограммах), а v – его скорость (в м/c), найдите m (в килограммах), если E = 500 Дж,
154. а) Используя формулу для вычисления кинетической энергии (в джоулях) E =
а v = 5 м/c.
mv 2
, где m – масса
2
тела (в килограммах), а v – его скорость (в м/c), найдите Е (в джоулях), если m = 50 кг, а v = 2 м/c.
а) Используя формулу для вычисления кинетической энергии (в джоулях) E =
155. а) Используя формулу для вычисления ускорения тела а (в м/c2) при его равномерном движении
по окружности a = ω2 R , где ω – угловая скорость вращения (в с-1), а R – радиус окружности
(в метрах), найдите a (в м/c2), если R = 9 м и ω = 2 с-1.
б) Используя формулу для вычисления ускорения тела а (в м/c2) при его равномерном движении
по окружности a = ω2 R , где ω – угловая скорость вращения (в с-1), а R – радиус окружности
(в метрах), найдите R (в метрах), если ω =3 с-1 и a = 18 м/c2.
U2
, где U – напряжение (в вольR
тах), R – сопротивление (в омах). Пользуясь этой формулой, найдите Р (в ваттах), если U = 15 В
156. а) Используя формулу для нахождения мощности (в ваттах) P =
и R = 5 Ом.
31
б) Используя формулу для нахождения мощности постоянного тока (в ваттах) вычисляется по
U2
формуле P =
, где U – напряжение (в вольтах), R – сопротивление (в омах), найдите U (в
R
вольтах), если P = 9 Вт и R = 25 Ом.
157. а) Найдите скорость камня (в м/с) в момент удара о землю, который падает с высоты 22,5 м,
используя формулу v = 2 gh , где h – высота (в метрах), с которой падает камень, а ускорение
свободного падения g равно 9,8 м/c2.
б) Найдите скорость камня (в м/с) в момент удара о землю, который падает с высоты 90 м,
используя формулу v = 2 gh , где h – высота (в метрах), с которой падает камень, а ускорение
свободного падения g равно 9,8 м/c2.
158. а) Используя формулу для вычисления потенциальной энергии тела (в джоулях) E = mgh , где
m – масса тела (в килограммах), g = 9,8 м/c2 – ускорение свободного падения, h – высота
(в метрах), на которой находится тело, относительно поверхности, найдите m (в килограммах),
если h = 10 м, а Е = 294 Дж.
б) Используя формулу для вычисления потенциальной энергии тела (в джоулях) E = mgh , где
m – масса тела (в килограммах), g = 9,8 м/c2 – ускорение свободного падения, h – высота
(в метрах), на которой находится тело, относительно поверхности, найдите Е (в джоулях), если
m = 5 кг, а h = 7 м.
U 2t
, где
R
U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах), найдите А
159. а) Используя формулу для вычисления работы постоянного тока (в джоулях) A =
(в джоулях), если t = 20 c, U = 6 В и R = 15 Ом.
б) Используя формулу для вычисления работы постоянного тока (в джоулях) A =
U 2t
, где U –
R
напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах), найдите U (в вольтах),
если t = 25 c, Е = 225 Дж и R = 9 Ом.
160. а) Используя
формулу для вычисления полученного телом при нагревании количества теÄæ
Äæ
Дж
Q cm(t2 − t1 ) , где с – удельная теплоёмкость кг · К , m – масса тела
плоты (в джоулях)=
êã⋅⋅ÊÊ
êã
(в килограммах), t1 – начальная температура тела (в кельвинах), а t2 – конечная температу-
ра тела (в кельвинах), найдите количество теплоты полученное телом (в джоулях), если
Дж
, t = 264 К, t1 = 194 К.
с = 520
кг · К 2
б) Используя формулу для вычисления полученного телом при нагревании количества теплоты
Äæ
Äæ
Дж
(в джоулях)=
Q cm(t2 − t1 ) , где с – удельная теплоёмкость кг · К , m – масса тела (в килоêã⋅⋅ÊÊ
êã
граммах), t1 – начальная температура тела (в кельвинах), а t2 – конечная температура тела
(в кельвинах), найдите количество теплоты полученное телом (в джоулях), если m = 4 кг,
Дж
, t = 305 К, t1 = 255 К.
кг · К 2
q2
,
161. а) Используя формулу для вычисления энергии заряженного конденсатора (в джоулях) W =
2C
где С – ёмкость конденсатора (в Фарадах), а q – заряд конденсатора (в Кулонах), найдите энерc = 640
гию конденсатора (в джоулях), если C= 2 ⋅ 10−5 Ф и q = 0,02 Кл.
CU 2
б) Используя формулу для вычисления энергии заряженного конденсатора (в джоулях) W =
,
2
где С – ёмкость конденсатора (в Фарадах), U – напряжение на конденсаторе (в вольтах), найдите
энергию конденсатора (в джоулях), если C= 6 ⋅ 10−4 Ф и U = 200 В.
32
162. а) Площадь поверхности прямоугольного параллелепипеда с рёбрами а, b, c вычисляется по
формуле S= 2(ab + ac + bc) . Найдите площадь поверхности прямоугольного параллелепипеда с
рёбрами 2, 3 и 4.
б) Площадь поверхности прямоугольного параллелепипеда с рёбрами а, b, c вычисляется по
формуле S= 2(ab + ac + bc) . Найдите а, если площадь поверхности прямоугольного параллелепипеда равна 286, а другие два ребра равны 5 и 9.
d 2 sin α
163. а) Используя формулу для вычисления площади прямоугольника S =
, где d – длина диа2
4
гонали, α – угол между диагоналями, найдите площадь треугольника S, если d = 15 , sin α = .
5
d 2 sin α
б) Используя формулу для вычисления площади прямоугольника S =
, где d – длина диа2
1
гонали, α – угол между диагоналями, найдите площадь треугольника S, если d = 6 , sin α = .
3
3
164. а) Среднее геометрическое трёх чисел a, b, c можно вычислить по формуле g = abc . Найдите
среднее геометрическое чисел 8, 64, 125.
б) Среднее геометрическое трёх чисел a, b, c можно вычислить по формуле g = 3 abc . Найдите среднее геометрическое чисел 12, 54, 72.
165. а) Площадь треугольника со сторонами a, b, c можно найти по формуле Герона
a+b+c
S=
p ( p − a )( p − b)( p − c) , где p =
. Найдите площадь треугольника, если длины его
2
сторон равны 13, 14 и 15.
б) Площадь треугольника со сторонами a, b, c можно найти по формуле Герона
a+b+c
S=
p ( p − a )( p − b)( p − c) , где p =
. Найдите площадь треугольника, если длины его
2
сторон равны 17, 65 и 80.
166. а) Используя формулу для вычисления радиуса окружности, описанной около треугольника,
a
, где а – сторона, а α – противолежащий ей угол треугольника, найдите радиус R,
R=
2sin α
7
если a = 14 и sin α = .
8
б) Используя формулу для вычисления радиуса окружности, описанной около треугольника,
a
, где а – сторона, а α – противолежащий ей угол треугольника, найдите сторону a,
R=
2sin α
5
если R = 12 и sin α = .
6
2
n(n + 1)
3
3
3
3
167. а) Известно, что 13 + 23 + 33 + ... + n3 =
. Найдите сумму 1 + 2 + 3 + ... + 9 .
2
2
n(n + 1)
3
3
3
3
б) Известно, что 13 + 23 + 33 + ... + n3 =
. Найдите сумму 1 + 2 + 3 + ... + 19 .
2
168. а) В фирме занимающейся грузоперевозками стоимость перевозки на грузовике рассчитывается
по формуле C = 1200 +150 · х, где х – количество километров до пункта назначения. Используя
эту формулу, рассчитайте стоимость перевозки груза на расстояние 23 километра.
б) В фирме занимающейся грузоперевозками стоимость перевозки на грузовике рассчитывается
по формуле C = 1300 +160 · х, где х – количество километров до пункта назначения. Используя
эту формулу, рассчитайте стоимость перевозки груза на расстояние 15 километров.
33
m1m2
, где F – сила притяжения между
r2
телами (в ньютонах), m1 и m2 – массы тел (в килограммах), r – расстояние между центрами масс
(в метрах), а γ – гравитационная постоянная, равная 6,67 · 10−11 H·м2/кг2, найдите массу тела m1
в килограммах, если F = 26,68 Н, m2 = 6·108 кг, r =3 м.
mm
б) Используя закон всемирного тяготения в виде F = γ 1 2 2 , где F – сила притяжения между
r
телами (в ньютонах), m1 и m2 – массы тел (в килограммах), r – расстояние между центрами масс
169. а) Используя закон всемирного тяготения в виде F = γ
(в метрах), а γ – гравитационная постоянная, равная 6,67 · 10−11 H·м2/кг2, найдите массу тела m1
в килограммах, если F = 20,01 Н, m2 = 64·107 кг, r =4 м.
170. а) Используя закон Менделеева-Клапейрона в виде PV = νRT, где P – давление (в паскалях),
V – объём (в м3), ν – количество вещества (в молях), T – температура (в градусах Кельвина), а
R – универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль), найдите температуру T в градусах Кельвина, если ν = 62,4 моль, P = 43212 Па, V = 6 м3.
б) Используя закон Менделеева-Клапейрона в виде PV = νRT, где P – давление (в паскалях),
V – объём (в м3), ν – количество вещества (в молях), T – температура (в градусах Кельвина),
а R – универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль), найдите температуру T в
градусах Кельвина, если ν = 86,4 моль, P = 53848,8 Па, V = 8 м3.
Проверочная работа № 9
1.
Вариант 1
1
=
S
d1d 2 sin α , где S – площадь произвольного четырёхугольника (в м2),
Используя формулу
2
d1, d 2 – его диагонали (в метрах), α – угол между диагоналями, найдите sin α , если площадь
четырёхугольника равна 150 м2, а диагонали – 10 м и 60 м.
2.
Используя формулу мощности постоянного тока P = I 2R, где P – мощность (в ваттах), I – сила
тока (в амперах), R – сопротивление (в омах), найдите сопротивление R в омах, если мощность
составляет 135 ватт, а сила тока равна 6 амперам.
3.
Найдите расстояние s (в метрах) от места удара молнии до наблюдателя, используя формулу для
приближённого вычисления этого расстояния s = 330t, где t – количество секунд, прошедших
между вспышкой молнии и раскатом грома, если наблюдатель услышал раскаты грома через 23 с
после вспышки молнии. Ответ дайте в километрах, округлив его до целых.
4.
В службе такси рассчитывают стоимость поездки, начиная с шестой минуты, по формуле
R = 530 + 15(t − 5) , где R – стоимость поездки (в рублях), t – время поездки (в минутах). Сколько
тысяч рублей составит цена поездки продолжительностью 101 минута?
5.
Длина медианы mc, проведённой к стороне c треугольника со сторонами а, b, c, вычисляется по
формуле mc =
2a 2 + 2b 2 − c 2
. Треугольник имеет стороны
2
проведённой к стороне длины 6.
34
11 , 5, 6. Найдите длину медианы,
Вариант 2
1.
1
d1d 2 sin α , где S – площадь произвольного четырёхугольника (в м2),
2
– его диагонали (в метрах), α – угол между диагоналями, найдите первую диагональ
=
S
Используя формулу
d1, d 2
5
8
четырёхугольника, если площадь четырёхугольника равна 130 м2, sin α = , а вторая диагональ 13 м.
2.
3.
4.
5.
Используя формулу центростремительного ускорения a = ω2R, где a – центростремительное
ускорение (в м/c2), ω – угловая скорость (в с−1), а R – радиус окружности (в метрах), найдите
радиус окружности в метрах, если угловая скорость равна 7 с−1, а центростремительное ускорение – 147 м/с2.
Найдите расстояние s (в метрах) от места удара молнии до наблюдателя, используя формулу для
приближённого вычисления этого расстояния s = 330t, где t – количество секунд, прошедших
между вспышкой молнии и раскатом грома, если наблюдатель услышал раскаты грома через
31 с после вспышки молнии. Ответ дайте в километрах, округлив его до целых.
В службе такси рассчитывают стоимость поездки, начиная с шестой минуты, по формуле
R = 370 + 16(t − 5) , где R – стоимость поездки (в рублях), t – время поездки в минутах. Найдите продолжительность поездки в часах, если её стоимость составила 2210 рублей?
Среднее квадратичное трёх чисел а, b, c вычисляется по формуле q =
формулой найдите среднее квадратичное чисел 5, 4 и
34 .
a 2 + b2 + c2
. Пользуясь
3
4.3. Простейшие текстовые задачи (округление)
171. а) В школе учится 326 детей и работает 32 учителя. Какое наименьшее количество автобусов
надо заказать для экскурсии, если в одном автобусе можно перевозить не более 35 пассажиров,
а на экскурсию поедут одновременно все дети и все учителя?
б) В школе учится 350 детей и работает 35 учителей. Какое наименьшее количество автобусов
надо заказать для экскурсии, если в одном автобусе можно перевозить не более 75 пассажиров,
а на экскурсию поедут одновременно все дети и все учителя?
172. а) В школе решили провести турпоход. Какое наименьшее число шестиместных палаток нужно
взять в поход, в котором участвует 135 человек?
б) В школе решили провести турпоход. Какое наименьшее число четырёхместных палаток нужно
взять в поход, в котором участвует 127 человек?
173. а) В школе на каждого ученика полагается 50 г сахара в день. В школе учится 193 человека. Какое наименьшее количество килограммовых упаковок сахара нужно на всех учеников на
4 дня?
б) В школе на каждого ученика полагается 30 г сахара в день. В школе учится 274 человека.
Какое наименьшее количество килограммовых упаковок сахара нужно на всех учеников на 3 дня?
174. а) В пачке 280 листов бумаги. За неделю в школе расходуется 900 листов. Какого наименьшего
количества пачек бумаги хватит на 5 недель?
б) В пачке 260 листов бумаги. За неделю в школе расходуется 850 листов. Какого наименьшего
количества пачек бумаги хватит на 7 недель?
35
175. а) За один день проведения кинофестиваля в среднем расходуется 120 бутылок воды. Кинофестиваль длится 4 дня. В одной упаковке 9 бутылок воды. Какого наименьшего количества упаковок
воды хватит на все дни кинофестиваля?
б) За один день проведения кинофестиваля в среднем расходуется 90 бутылок воды. Кинофестиваль длится 6 дней. В одной упаковке 13 бутылок воды. Какого наименьшего количества
упаковок воды хватит на все дни кинофестиваля?
176. а) Лайнер рассчитан на 690 пассажиров и 32 членов команды. Каждая спасательная шлюпка
может вместить 70 человек. Какое наименьше число шлюпок должно быть на лайнере, чтобы в
случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
б) Лайнер рассчитан на 620 пассажиров и 41 члена команды. Каждая спасательная шлюпка
может вместить 50 человек. Какое наименьше число шлюпок должно быть на лайнере, чтобы в
случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
177. а) Творожок стоит 40 рублей. В понедельник в магазине проходит акция: заплатив за два творожка, покупатель получает три (один в подарок). Сколько творожков можно получить на
260 рублей в понедельник?
б) Творожок стоит 30 рублей. В среду в магазине проходит акция: заплатив за три творожка, покупатель получает четыре (один в подарок). Сколько творожков можно получить на
260 рублей в среду?
178. а) Стоимость проездного билета на месяц составляет 960 рублей, а стоимость билета на одну
поездку 38 рублей. Сергей купил проездной и сделал за месяц 35 поездок. На сколько рублей
больше он бы потратил, если бы покупал билеты на одну поездку?
б) Стоимость проездного билета на месяц составляет 1870 рублей, а стоимость билета на одну
поездку 54 рубля. Валера купил проездной и сделал за месяц 45 поездок. На сколько рублей
больше он бы потратил, если бы покупал билеты на одну поездку?
179. а) Килограмм земляники стоит 330 рублей. Люба купила 2 кг 500 г земляники. Сколько рублей
сдачи она получила с 1000 рублей?
б) Килограмм черешни стоит 270 рублей. Света купила 3 кг 500 г черешни. Сколько рублей
сдачи она получила с 1000 рублей?
180. а) Стоимость выкапывания колодца рассчитывается следующим образом: первый метр стоит
3600 рублей, а каждый следующий метр – на 1200 рублей больше, чем предыдущий. Сколько
рублей стоит выкапывание колодца глубиной 13 метров?
б) Стоимость выкапывания колодца рассчитывается следующим образом: первый метр стоит
4100 рублей, а каждый следующий метр – на 1500 рублей больше, чем предыдущий. Сколько
рублей стоит выкапывание колодца глубиной 15 метров?
181. а) Стоимость годовой подписки на газету составляет 1650 рублей. Стоимость одного выпуска
газеты в магазине – 72 рубля. За год Ирина купила 24 выпуска газеты. На сколько рублей меньше
она бы потратила, если бы купила годовую подписку на газету?
б) Стоимость годовой подписки на газету составляет 1470 рублей. Стоимость одного выпуска
газеты в магазине – 47 рублей. За год Вера купила 36 выпусков газеты. На сколько рублей
меньше она бы потратила, если бы купила годовую подписку на газету?
182. а) Роман хочет подарить своей маме букет пионов из нечётного числа цветов. Один цветок стоит
60 рублей. У Романа есть 500 рублей. Из какого наибольшего числа пионов он может купить
букет маме на праздник?
36
б) Алексей хочет подарить своей маме букет роз из нечётного числа цветов. Один цветок стоит
90 рублей. У Алексея есть 700 рублей. Из какого наибольшего числа роз он может купить букет
маме на праздник?
183. а) Спортивный батончик стоит 27 рублей. Какое наибольшее количество спортивных батончиков
можно купить на 220 рублей?
б) Спортивный батончик стоит 31 рубль. Какое наибольшее количество спортивных батончиков
можно купить на 420 рублей?
184. а) Владимир за месяц проехал 7000 км. Средний расход бензина на 100 км составляет 9 литров.
Сколько рублей потратил Владимир на бензин за этот месяц, если цена бензина составляет
54 рублей за литр?
б) Дмитрий за месяц проехал 9000 км. Цена бензина 58 рублей за литр. Средний расход бензина
на 100 км составляет 11 литров. Сколько рублей потратил Дмитрий на бензин за этот месяц,
если цена бензина составляет 58 рубля за литр?
185. а) Молоко можно купить на разлив, заплатив при этом за саму бутылку и за молоко, которое в
неё налито. Бутылка молока объёмом 1 литр стоит 48 рублей, а объёмом 2 литра – 78 рублей.
Сколько рублей будет стоить бутылка молока объёмом 2,5 литра, если цена бутылки не зависит
от её объёма?
б) Молоко можно купить на разлив, заплатив при этом за саму бутылку и за молоко, которое в
неё налито. Бутылка молока объёмом 1 литр стоит 58 рублей, а объёмом 1,5 литра – 79 рублей.
Сколько рублей будет стоить бутылка молока объёмом 2 литра, если цена бутылки не зависит
от её объёма?
186. а) На автозаправочной станции Николай отдал оператору 2000 рублей, чтобы залить бензин до
полного бака. Цена бензина 55 рублей за литр. После окончания заправки Николай получил
350 рублей сдачи. Сколько литров бензина было залито в бак?
б) На автозаправочной станции Александр отдал оператору 5000 рублей, чтобы залить бензин до
полного бака. Цена бензина 59 рублей за литр. После окончания заправки Александр получил
2345 рублей сдачи. Сколько литров бензина было залито в бак?
187. а) Фильм размером 4 Гб скачался за 22 минуты (скорость загрузки постоянная). За сколько минут
скачается фильм размером 3,6 Гб с той же скоростью загрузки?
б) Фильм размером 2400 Мб скачался за 12 минут (скорость загрузки постоянная). За сколько
минут скачается фильм размером 1500 Мбайт с той же скоростью загрузки?
188. а) Принтер печатает одну страницу за 8 секунд. Какое наибольшее количество страниц можно
напечатать на этом принтере за 14 минут?
б) Принтер печатает одну страницу за 12 секунд. Какое наибольшее количество страниц можно
напечатать на этом принтере за 24 минуту?
189. а) Для ремонта загородного дома требуется 69 рулонов обоев. Сколько пачек обойного клея
нужно купить для такого ремонта, если 1 пачка клея рассчитана на 8 рулонов?
б) Для ремонта загородного дома требуется 75 рулонов обоев. Сколько пачек обойного клея
нужно купить для такого ремонта, если 1 пачка клея рассчитана на 11 рулонов?
190. а) В квартире установлен прибор учёта электроэнергии (однотарифный счётчик). Показания
счётчика 1 февраля составляли 573 кВт·ч, а 1 марта – 621 кВт·ч. Сколько нужно заплатить за
электроэнергию за февраль, если стоимость одного киловатт–часа энергии составляет 5,5 рубля?
Ответ дайте в рублях.
37
б) В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика
1 июня составляли 794 куб. м воды, а 1 июля – 803 куб. м. Сколько нужно заплатить за холодную воду за июнь, если стоимость одного куба холодной воды составляет 43 рубля? Ответ
дайте в рублях.
191. а) На какой высоте в метрах летит самолёт, если он поднялся на 24 000 фута над землёй, а
1 фут равен 30,5 см?
б) На какой высоте в метрах летит самолёт, если он поднялся на 15 000 фута над землёй, а
1 фут равен 30,5 см?
192. а) Автомобиль движется со скоростью 56 км/ч. Какую скорость показывает спидометр этого
автомобиля в милях в часах, если одна миля равна 1,6 км?
б) Автомобиль движется со скоростью 68 км/ч. Какую скорость показывает спидометр этого
автомобиля в милях в часах, если одна миля равна 1,6 км?
193. а) По расписанию автобус Санкт–Петербург – Москва отправляется в 15:37, а прибывает в 1:37
на следующий день (время московское). Сколько часов автобус находится в пути?
б) По расписанию поезд Москва – Тамбов отправляется в 6:34, а прибывает в 0:34 на следующий
день (время московское). Сколько часов поезд находится в пути?
194. а) Найдите, на каком этаже находится квартира Инны, если известно, что она живёт в квартире
№ 71, в её доме один подъезд, а на каждом этаже по шесть квартир.
б) Найдите, на каком этаже находится квартира Насти, если известно, что она живёт в квартире
№ 68, в её доме один подъезд, а на каждом этаже по восемь квартир.
195. а) Пешеход прошёл за 50 минут 4 километра. Сколько километров он пройдёт за 1 час, если
будет идти с той же скоростью?
б) Пешеход прошёл за 45 минут 6 километров. Сколько километров он пройдёт за 2 часа, если
будет идти с той же скоростью?
196. а) Велосипедист проехал 15 километров за 24 минуты. Сколько километров он проедет
за 20 минут, если будет ехать с той же скоростью?
б) Велосипедист проехал 12 километров за 40 минут. Сколько километров он проедет
за 1,5 часа, если будет ехать с той же скоростью?
Проверочная работа № 10
Вариант 1
1.
В школе на каждого ученика полагается 30 г сахара в день. В школе учится 456 человек. Какое
2.
наименьшее количество килограммовых упаковок сахара нужно на всех учеников на 5 дней?
Стоимость проездного билета на месяц составляет 1980 рублей, а стоимость билета на одну
3.
поездку 47 рублей. Сергей купил проездной и сделал за месяц 48 поездок. На сколько рублей
больше он бы потратил, если бы покупал билеты на одну поездку?
Фильм размером 6 Гб скачался за 32 минут (скорость загрузки постоянная). За сколько минут
4.
38
скачается фильм размером 4,8 Гб с той же скоростью загрузки?
Велосипедист проехал 11 километров за 22 минуты. Сколько километров он проедет
за 10 минут, если будет ехать с той же скоростью?
Вариант 2
1.
За один день проведения кинофестиваля в среднем расходуется 130 бутылок воды. Кинофестиваль длится 7 дней. В одной упаковке 12 бутылок воды. Какого наименьшего количества
упаковок воды хватит на все дни кинофестиваля?
2.
Стоимость годовой подписки на газету составляет 2650 рублей. Стоимость одного выпуска
газеты в магазине – 48 рублей. За год Ирина купила 72 выпуска газеты. На сколько рублей
меньше она бы потратила, если бы купила подписку на газету?
3.
Принтер печатает одну страницу за 12 секунд. Какое наибольшее количество страниц можно
напечатать на этом принтере за 23 минуты?
4.
Пешеход прошёл за 48 минут 4 километра. Сколько километров он пройдёт за 3,5 часа, если
будет идти с той же скоростью?
4.4. Простейшие текстовые задачи (части)
197. а) Для приготовления варенья взяли малину и смородину в отношении 13:7 соответственно.
Сколько процентов всех ягод составляет малина?
б) Для приготовления варенья взяли малину и смородину в отношении 7:3 соответственно.
Сколько процентов всех ягод составляет малина?
198. а) Акции корпорации распределены между государством и частными инвесторами в отношении
11:1 соответственно. Корпорация объявила дивиденды по итогам года – 48 млн. рублей. Какая
сумма должна пойти на выплаты частным инвесторам? Ответ дайте в миллионах рублей.
б) Акции корпорации распределены между государством и частными инвесторами в отношении
19:1 соответственно. Корпорация объявила дивиденды по итогам года – 60 млн. рублей. Какая
сумма должна пойти на выплаты частным инвесторам? Ответ дайте в миллионах рублей.
199. а) В саду растут яблони и груши. Число яблонь относится к числу груш как 18:7. Сколько процентов деревьев в саду составляют яблони?
б) В саду растут яблони и груши. Число яблонь относится к числу груш как 11:9. Сколько процентов деревьев в саду составляют яблони?
200. а) Площадь земель в посёлке составляет 48 гектаров и распределена между муниципалитетом
и частными собственниками в соотношении 7:5 соответственно. Сколько гектаров занимают
частные земли?
б) Площадь земель в посёлке составляет 50 гектаров и распределена между муниципалитетом
и частными собственниками в соотношении 7:3 соответственно. Сколько гектаров занимают
муниципальные земли?
201. а) При проведении выборов главы управы муниципалитета на пост претендовали два кандидата.
В голосовании приняли участие 81 человек. Голоса распределились в соотношении 5:4. Сколько
голосов получил победитель?
б) При проведении выборов главы управы муниципалитета на пост претендовали два кандидата.
В голосовании приняли участие 80 человек. Голоса распределились в соотношении 7:3. Сколько
голосов получил победитель?
39
202. а) Победителями олимпиады по математике стали 36 учащихся, что составляет 3% от числа всех
участников. Сколько человек участвовало в олимпиаде?
б) Победителями олимпиады по математике стали 27 учащихся, что составляет 5% от числа
всех участников. Сколько человек участвовало в олимпиаде?
203. а) Пакет молока стоит 120 рублей. Магазин делает скидку пенсионерам 20%. Сколько рублей
стоит пакет молока для пенсионера?
б) Пакет молока стоит 140 рублей. Магазин делает скидку пенсионерам 15%. Сколько рублей
стоит пакет молока для пенсионера?
204. а) В Москве проживает примерно 12,5 миллионов человек, из них 24% – пенсионеры. Сколько
пенсионеров проживает в Москве? Ответ дайте в миллионах человек.
б) В Санкт-Петербурге проживает примерно 5 миллионов человек, из них 3 миллиона – работающие. Сколько процентов работающих людей проживает в Санкт-Петербурге?
205. а) Летом килограмм клубники стоит 85 рублей. Осенью клубника подорожала на 40%. Сколько
рублей стоит килограмм клубники осенью?
б) Летом килограмм черешни стоит 120 рублей. Осенью черешня подорожала на 30%. Сколько
рублей стоит килограмм черешни осенью?
206. а) В магазине электронных товаров дважды проходила распродажа. Во время первой распродажи
магазин снизил цены на 10%, во время второй – ещё на 25%. Сколько рублей стал стоить утюг
после второго снижения цен, если до начала распродаж его цена была 2600 рублей?
б) В магазине электронных товаров дважды проходила распродажа. Во время первой распродажи
магазин снизил цены на 15%, во время второй – ещё на 20%. Сколько рублей стала стоить микроволновая печь после второго снижения цен, если до начала распродаж её цена была 7000 рублей?
207. а) Абонентская плата за мобильную связь составляет 450 рублей в месяц. В следующем году
оператор объявил о повышении платы на 6%. Сколько рублей будет составлять абонентская
плата в следующем году?
б) Абонентская плата за мобильную связь составляет 350 рублей в месяц. В следующем году
оператор объявил о повышении платы на 4%. Сколько рублей будет составлять абонентская
плата в следующем году?
208. а) Банк начисляет 11% годовых по вкладу. Вкладчик положил на счёт 15000 рублей. Сколько
рублей будет на счёте через год?
б) Банк начисляет 9% годовых по вкладу. Вкладчик положил на счёт 17000 рублей. Сколько
рублей будет на счёте через год?
209. а) Городской бюджет Санкт-Петербурга составляет 170 млрд. рублей. Одна из запланированных
статей расхода – потратить 12% бюджета на поддержку памятников архитектуры. Сколько миллиардов рублей планируется потратить из городского бюджета по этой статье?
б) Городской бюджет составляет 120 млрд. рублей. Одна из запланированных статей расхода –
потратить 15% бюджета на социальные выплаты. Сколько миллиардов рублей планируется потратить из городского бюджета по этой статье?
210. а) Поступивший летом в продажу новый смартфон стоит 32000 рублей. Осенью он стал стоить
40000 рублей. На сколько процентов повысилась цена смартфона за этот период?
б) Поступивший летом в продажу новый смартфон стоит 30000 рублей. Осенью он стал стоить
42000 рублей. На сколько процентов повысилась цена смартфона за этот период?
40
211. а) Набор посуды, который стоил 3000 рублей, продается теперь со скидкой 15%. Сколько рублей
стоят два таких набора со скидкой?
б) Чайный сервиз, который стоил 5000 рублей, продается теперь со скидкой 20%. Сколько рублей
стоят два таких чайных сервиза со скидкой?
212. а) На экономическом факультете собираются учиться 87 выпускника школы. Они составляют
60% от числа всех выпускников. Сколько в школе выпускников?
б) На физико-математическом факультете собираются учиться 93 выпускника школы. Они составляют 62% от числа всех выпускников. Сколько в школе выпускников?
213. а) В начале учебного года на первом курсе университета было 620 студентов. К концу года их
стало 589. На сколько процентов уменьшилось число первокурсников за год?
б) В начале учебного года на первом курсе университета было 650 студентов. К концу года их
стало 598. На сколько процентов уменьшилось число первокурсников за год?
214. а) В начале года число вкладчиков банка составляло 2 миллиона человек, а к концу года число
вкладчиков увеличилось до 3,2 миллионов человек. На сколько процентов выросло число вкладчиков за год?
б) В начале года число вкладчиков банка составляло 2 миллиона человек, а к концу года число вкладчиков увеличилось до 3,6 миллионов человек. На сколько процентов выросло число
вкладчиков за год?
215. а) В июне портфель стоил 1400 рублей, в июле он подорожал на 15%, а в августе – ещё на 20%.
Сколько стоил портфель в августе после всех подорожаний?
б) В июне портфель стоил 1600 рублей, в июле он подорожал на 20%, а в августе – ещё на 30%.
Сколько стоил портфель в августе после всех подорожаний?
216. а) Школьная тетрадь стоит 15 рублей. Сколько рублей заплатит Ваня за 70 тетрадей, если при
покупке более 50 тетрадей магазин делает скидку 20% от стоимости всей покупки?
б) Школьная тетрадь стоит 17 рублей. Сколько рублей заплатит Денис за 80 тетрадей, если при
покупке более 60 тетрадей магазин делает скидку 15% от стоимости всей покупки?
217. а) Из 4000 рублей Мария потратила 95% на покупку продуктов, а оставшиеся деньги отложила.
Сколько рублей Мария отложила?
б) Из 2500 рублей Екатерина потратила 83% на покупку косметики, а оставшиеся деньги отложила. Сколько рублей Екатерина отложила?
218. а) После снижения цены на 15% платье стало стоить 5950 рублей. Сколько рублей стоило платье
до распродажи?
б) После снижения цены на 35% платье стало стоить 5525 рублей. Сколько рублей стоило платье
до распродажи?
219. а) Летом в городе число больных простудой уменьшилось в 5 раз. На сколько процентов уменьшилось число больных простудой летом в этом городе?
б) Зимой в городе число больных простудой увеличилось в 4 раза. На сколько процентов увеличилось число больных простудой зимой в этом городе?
220. а) Три процента числа 400 равны 10% числа а. Найдите число а.
б) Семь процентов числа 200 равны 40% числа а. Найдите число а.
41
221. а) Цена товара увеличилась на 25%. На сколько процентов ее необходимо уменьшить, чтобы
получить первоначальное значение?
б) Вклад, пролежавший в банке один год, в конце этого года увеличился на 20%. На сколько
процентов увеличится первоначальная сумма вклада, пролежавшего в банке два года, при постоянном банковском проценте?
Проверочная работа № 11
Вариант 1
1.
2.
3.
4.
Для приготовления варенья взяли малину и смородину в отношении 13:12 соответственно.
Какой процент в варенье составляет малина?
Пакет молока стоит 155 рублей. Магазин делает скидку пенсионерам 24%. Сколько рублей
стоит пакет молока для пенсионера?
Победителями олимпиады по математике стали 45 учащихся, что составляет 12% от числа всех
участников. Сколько человек участвовало в олимпиаде?
Летом в городе число больных простудой уменьшилось в 2,5 раз. На сколько процентов уменьшилось число больных простудой летом в этом городе?
Вариант 2
1.
2.
3.
4.
В саду растут яблони и груши. Число яблонь относится к числу груш как 23:27. Сколько процентов деревьев в саду составляют яблони?
Летом килограмм клубники стоит 178 рублей. Осенью клубника подорожала на 60%. Сколько
рублей стоит килограмм клубники осенью?
На экономическом факультете собираются учиться 105 выпускников школы. Они составляют
60% от числа всех выпускников. Сколько в школе выпускников?
В начале года число вкладчиков банка составляло 4 миллиона человек, а к концу года число вкладчиков увеличилось до 5,2 миллионов человек. На сколько процентов выросло число
вкладчиков за год?
4.5. Выбор оптимального варианта
222. Покупатель хочет купить смартфон определенной модели. В таблице показано 5 предложений
от различных магазинов. Покупатель не хочет делать покупку в магазине, рейтинг которого
ниже 4. Среди магазинов, удовлетворяющих этому условию, выберите предложение с самой
низкой стоимостью покупки с учётом стоимости доставки. В ответе запишите стоимость покупки вместе с доставкой в рублях.
42
Номер магазина
Рейтинг
Стоимость (руб.)
Стоимость доставки
(руб.)
1
3
70999
999
2
5
71999
999
3
4
72499
500
4
5
73000
700
5
4
72799
300
223. В музейном комплексе имеется пять выставок: A, B, C, D, E. В кассе продаётся шесть видов
билетов, каждый из которых позволяет посетить одну или две выставки. Сведения о стоимости
билетов представлены в таблице. Какие билеты должен купить посетитель, чтобы посетить все
выставки и потратить не больше 750 рублей? В ответе укажите какой-нибудь набор номеров
билетов без пробелов и запятых.
Номер билета
Выставки, входящие
в стоимость билета
Стоимость билета (руб.)
1
A, B
300
2
A, C
400
3
B, D
400
4
C
150
5
D, E
300
6
C, E
350
224. Анатолий хочет посетить четыре города России: Великий Новгород, Тверь, Бежецк и Рыбинск.
Турфирма предлагает туры с посещением этих городов. Условия туров представлены в таблице.
Какие туры должен выбрать Анатолий, чтобы побывать во всех четырёх нужных ему городах
и потратить на поездки менее 20000 рублей? В ответе укажите какой-нибудь набор туров без
пробелов и запятых.
Номер тура
Города в туре
Стоимость тура
1
Бежецк, Тверь, Великий Новгород
15600
2
Рыбинск, Великий Новгород
9600
3
Тверь, Великий Новгород
8400
4
Бежецк
6600
5
Рыбинск, Бежецк
10800
6
Тверь, Рыбинск
9400
225. Турист, приехавший в Рязань, хочет посетить 4 достопримечательности: Соборный парк, Успенский собор, музей С.А. Есенина и Рязанский кремль. Экскурсионные бюро предлагают маршруты
с посещением одного или нескольких объектов. Сведения о стоимости представлены в таблице.
Какие маршруты должен купить турист, чтобы посетить все четыре объекта и потратить как
можно меньшую сумму? В ответе укажите эту сумму в рублях.
Номер
маршрута
Объекты
Стоимость
1
Соборный парк
900
2
музей С.А.Есенина, Рязанский кремль
4050
3
Рязанский кремль
900
4
Соборный парк, Успенский собор
4200
5
музей С.А.Есенина, Успенский собор
4950
6
Успенский собор
1950
43
226. Цена электроэнергии по однотарифному счётчику составляет 5,7 руб. за 1 кВт·ч. Цена электроэнергии по двухтарифному счётчику в дневное время – 6,9 руб. за 1 кВт·ч, в ночное время –
2,6 руб. за 1 кВт·ч. Житель города тратит в месяц 100 кВт·ч в дневное время и 120 кВт·ч в ночное. Рассчитайте, сколько рублей сэкономит житель при использовании двухтарифного счётчика
по сравнению с однотарифным за 12 месяцев (один год). В ответ запишите сумму в рублях.
227. Путешественнику необходимо арендовать автомобиль для поездки протяженностью 600 км на
двое суток. Он присмотрел три автомобиля в фирме занимающейся арендой автомобилей. Условия аренды представлены в таблице. Помимо стоимости аренды, путешественник также оплачивает топливо для автомобиля. Цена дизельного топлива – 40 рублей за литр, бензина – 52 рубля
за литр, газа – 30 рублей за литр. Какую сумму заплатит клиент за аренду и топливо, если хочет
выбрать самый дешевый вариант? В ответе запишите эту сумму в рублях.
Автомобиль
Топливо
Расход топлива
(л на 100 км)
Арендная плата
(руб. за 1 сутки)
1
Дизельное
10
3200
2
Бензин
8
3000
3
Газ
12
3100
228. Три фирмы предлагают услуги по грузоперевозкам. Стоимость услуг, предоставляемых фирмами,
приведены в таблице. Необходимо перевезти 22 тонны груза на 1300 км. Сколько рублей нужно
заплатить за самую дешёвую перевозку в одной из этих фирм?
Номер фирмы
Стоимость перевозки одним грузовиком
(руб. на 100 км)
Грузоподъёмность одного
грузовика (тонны)
1
3200
5
2
3800
7
3
5000
10
229. Международной корпорации для организации конференции необходимо нанять переводчиков
для обеспечения синхронного перевода докладчиков. В таблице представлены сведения о шести
кандидатах. Корпорация собирается потратить на услуги переводчиков не более 18000 рублей
и при этом собрать группу переводчиков, в которой все кандидаты вместе владеют четырьмя
разными языками. В ответе укажите какой-нибудь подходящий набор переводчиков без пробелов
и запятых.
44
Переводчики
Языки
Стоимость услуг
1
Немецкий, китайский
10500
2
Английский, немецкий
9000
3
Английский
4500
4
Английский, французский
9000
5
Французский
3000
6
Китайский
6000
230. Иван и Юлия с двумя дочерями собираются поехать из Москвы в Екатеринбург. Они рассматривают два варианта поездки: на поезде и на личном автомобиле. Билет на поезд на одного
человека стоит 2100 рублей. Автомобиль расходует 8 литров бензина на 100 километров пути,
расстояние по автостраде до Екатеринбурга равно 1800 км, а цена бензина равна 52 рубля за
литр. Сколько рублей придётся потратить на наиболее дешёвую поездку в Екатеринбург для всей
семьи?
231. При строительстве деревенского магазина можно сделать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 3 тонны камня и 3 мешка цемента.
Для бетонного фундамента необходимо 4 тонны щебня и 30 мешков цемента. Тонна камня стоит
3200 рублей, тонна щебня – 700 рублей, а один мешок цемента – 350 рублей. Сколько рублей
будет стоить наиболее дешёвый вариант фундамента?
232. Артём сдал ЕГЭ по четырём предметам: по русскому языку – на 60 баллов, по математике – на
60 баллов, по физике – на 50 баллов, по информатике – на 70 баллов. В таблице приведены
минимальные баллы ЕГЭ по четырём предметам, необходимые для подачи документов на факультеты 1-6. Укажите номера факультетов, на которые сможет подать документы Артём. Ответ
запишите без пробелов и запятых.
Факультет
Русский язык
Математика
Физика
Информатика
1
52
60
60
70
2
30
60
50
60
3
45
65
40
68
4
50
60
65
60
5
60
56
70
75
6
80
80
75
87
233. Алексей собирается купить 50 кубометров пиломатериалов у одного из трёх поставщиков. Сведения о поставщиках указаны в таблице. Сколько рублей Алексею придётся заплатить за самую
дешёвую покупку с доставкой?
Поставщик
Стоимость пиломатериалов (руб. за 1 кубометр)
Стоимость доставки (руб.)
Дополнительные условия
А
29500
10000
нет
30000
При заказе на сумму свыше
2 млн.руб. доставка
бесплатная
40000
При заказе на сумму свыше
1 млн.руб. доставка
бесплантая
Б
В
27000
27500
234. Евгении и её пяти друзьям необходимо сдать в багаж чемоданы. Сведения об этих чемоданах
приведены в таблице. Для перевозки авиакомпанией сумма трёх измерений (длина, высота, ширина) багажа, не должна превышать 203 см, а масса не должна быть больше 20 кг. Какие чемоданы авиакомпания позволит перевести? В ответе укажите номера всех подходящих багажей
без пробелов и запятых.
45
Номер багажа
Длина (см)
Высота (см)
Ширина (см)
Масса (кг)
1
34
42
18
19
2
55
110
42
17
3
45
74
29
23
4
57
85
33
25
5
59
92
34
18,5
6
60
127
31
20
235. Турист собирается в поездку на трое суток. В таблице дана информация о гостиницах в городе
назначения. Турист хочет остановиться в гостинице, которая находится не дальше чем 3,5 км
от центра города и рейтинг которой не ниже 8. Среди шести гостиниц выберете гостиницу с
наименьшей ценой номера за сутки. Укажите в ответе стоимость проживания в этой гостинице
за трое суток в рублях.
Номер гостиницы
Рейтинг
Расстояние до центра (км) Стоимость в сутки (руб.)
1
7
2
3500
2
8,8
4
3000
3
9,2
2,3
3450
4
8,7
1
3300
5
6,5
2,3
3050
6
9
3,8
3100
236. Шкаф–купе можно купить в кредит в трёх мебельных магазинах. Условия продажи представлены
в таблице. Определите, в каком из магазинов покупка обойдется дешевле всего (с учётом переплаты). В ответе укажите стоимость покупки в рублях.
Магазин
Стоимость
шкафа-купе
(руб.)
Первоначальный
взнос
(% от стоимости)
Срок кредита
(мес.)
Сумма ежемесячного платежа
(руб.)
А
54100
15
6
8680
Б
54200
25
6
8280
В
55000
25
12
3620
237. Варвара хочет купить платье за 6500 рублей. В магазине при предъявлении дисконтной карты
предоставляется скидка на платье в размере 15% от его стоимости, стоимость дисконтной карты
400 рублей. Варвара может оплатить платье по полной стоимости или сначала купить карту и
купить платье со скидкой. Сколько рублей составит стоимость наиболее выгодной покупки?
238. Екатерине нужно облицевать плиткой участок стены на кухне – квадрат со стороной 2 м. Она выбирает
из трёх видов плитки, информация о которых представлена в таблице. Во сколько рублей обойдется
наиболее дешёвый вариант покупки, если известно, что плитка продаётся только упаковками?
46
Площадь одной плитки,
см2
Количество плиток
в упаковке
Цена упаковки, руб.
1
400
20
600
2
600
16
570
3
900
12
650
Проверочная работа № 12
Вариант 1
Три фирмы предлагают услуги по грузоперевозкам. Стоимость услуг, предоставляемых фирмами,
приведены в таблице. Необходимо перевезти 35 тонн груза на 800 км. Сколько рублей нужно заплатить за самую дешёвую перевозку в одной из этих фирм ?
Номер фирмы
Стоимость перевозки одним грузовиком
(руб. на 100 км)
Грузоподъёмность одного
грузовика (тонны)
1
3900
6
2
4300
8
3
5500
10
Вариант 2
Алексей собирается купить 40 кубометров пиломатериалов у одного из трёх поставщиков. Сведения о поставщиках указаны в таблице. Сколько рублей Алексею придётся заплатить за самую
дешёвую покупку с доставкой?
Поставщик
Стоимость
пиломатериалов
(руб. за 1 кубометр)
Стоимость
доставки (руб.)
Дополнительные условия
А
41700
15000
нет
Б
39500
45000
при заказе на сумму свыше
2 млн.руб. доставка бесплатная
В
40300
35000
при заказе на сумму свыше
1 млн.руб. доставка бесплантая
4.6. Текстовые задачи (движение, работа, растворы)
Задачи на движение по прямой
239. а) Из пунктов А и В, расстояние между которыми 16 км, вышли одновременно навстречу друг
другу два пешехода и встретились в 10 км от А. Найдите скорость пешехода, шедшего из А, если
известно, что он шёл со скоростью, на 4 км/ч большей, чем пешеход, шедший из В, и сделал
в пути остановку на 15 минут. Ответ дайте в км/ч.
б) Из пунктов А и В, расстояние между которыми 18 км, вышли одновременно навстречу друг
другу два пешехода и встретились в 8 км от В. Найдите скорость пешехода, шедшего из А, если
известно, что он шёл со скоростью, на 2 км/ч большей, чем пешеход, шедший из В, и сделал в
пути остановку на 40 минут. Ответ дайте в км/ч.
240. а) Начав движение одновременно из пунктов А и В навстречу друг другу, велосипедист и бегун
встретились через 30 минут. За сколько минут бегун преодолеет расстояние между пунктами,
если велосипедисту для этого потребуется 45 минут?
47
б) Начав движение одновременно из пунктов А и В навстречу друг другу, велосипедист и бегун
встретились через 24 минуты. За сколько минут велосипедист преодолеет расстояние между
пунктами, если бегуну для этого потребуется 1 час 12 минут?
241. а) Два мотоциклиста выехали одновременно с одинаковой скоростью из пункта А в пункт В,
находящимися друг от друга на расстоянии 100 км. Через 30 мин после начала движения у одного из них случился прокол и ему пришлось остановиться для замены колеса. Потратив на это
15 мин, он продолжил движение, увеличив первоначальную скорость на 10 км/час, и прибыл
в пункт В одновременно с мотоциклистом, двигавшимся без остановок. За сколько часов они
преодолели путь из А в В?
б) Из пункта А в одном направлении выехали одновременно с одинаковой скоростью два мотоциклиста. Через 30 мин после начала движения у одного из них случился прокол и ему пришлось
остановиться для замены колеса. Потратив на это 15 мин, он продолжил движение, увеличив
первоначальную скорость на 10 км/час, догнал мотоциклиста, двигавшегося без остановок. Определите, на каком расстоянии от пункта А он догнал другого мотоциклиста, если с момента их
выезда из пункта А прошло ровно 2 часа. Ответ дайте в километрах.
242. а) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 56 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет
154 км, скорость первого велосипедиста равна 13 км/ч, скорость второго – 15 км/ч. Определите
расстояние в километрах, которое проехал до места встречи второй велосипедист.
б) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 15 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет
166 км, скорость первого велосипедиста равна 16 км/ч, скорость второго – 24 км/ч. Определите
расстояние в километрах, которое проехал до места встречи второй велосипедист.
243. а) Два автомобиля одновременно отправляются из пункта А в пункт В, расстояние между которыми равно 280 км. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает в
пункт В на 40 минут раньше второго. Найдите скорость первого автомобиля в км/ч.
б) Два автомобиля одновременно отправляются из пункта А в пункт В, расстояние между которыми равно 390 км. Первый едет со скоростью на 18 км/ч большей, чем второй, и прибывает в
пункт В на 1,5 часа раньше второго. Найдите скорость второго автомобиля в км/ч.
244. а) Из А в В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью
весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобиля на 9 км/ч, а вторую половину пути проехал со скоростью 84 км/ч, в результате чего
прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля в км/ч,
если известно, что она больше 50 км/ч.
б) Из А в В одновременно выехали два автомобиля. Первый пxроехал с постоянной скоростью
весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого
автомобиля на 16 км/ч, а вторую половину пути проехал со скоростью 120 км/ч, в результате
чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля
в км/ч, если известно, что она больше 80 км/ч.
245. а) Из пунктов А и В навстречу друг другу одновременно выехали велосипедист и мотоциклист.
Во сколько раз скорость мотоциклиста больше скорости велосипедиста, если известно, что они
встретились в пути через 70 минут после начала движения, и велосипедист преодолел расстояние
между пунктами за 3,5 часа?
48
б) Расстояние между пунктами А и В один их двух путешественников проходит за 2 часа. За
сколько минут преодолеет это расстояние другой из них, если, выйдя одновременно из пунктов
А и В навстречу друг другу, они встретятся через 1 час 12 минут?
Задачи на движение по замкнутой трассе
246. а) Два велосипедиста стартуют в одном направлении из двух диаметрально противоположных
точек круговой трассы, длина которой 8 км. Известно, что скорость одного из них на 5 км/ч
больше скорости второго. Через сколько минут велосипедисты поравняются в первый раз?
б) Два велосипедиста стартуют в одном направлении из двух диаметрально противоположных
точек круговой трассы, длина которой 10 км. Известно, что скорость одного из них на 6 км/ч
больше скорости второго. Через сколько минут велосипедисты поравняются в первый раз?
247. а) Два велосипедиста стартуют в одном направлении из одной точки круговой трассы, длина
которой 6 км. Скорость первого велосипедиста равна 20 км/ч, и через 40 минут после старта он
опережал второго велосипедиста на один круг. Найдите скорость второго велосипедиста в км/ч.
б) Два велосипедиста стартуют в одном направлении из одной точки круговой трассы, длина
которой 5 км. Скорость первого велосипедиста равна 22 км/ч, и через 50 минут после старта он
опережал второго велосипедиста на один круг. Найдите скорость второго велосипедиста в км/ч.
Задачи на движение протяжённых тел
248. а) Поезд, двигаясь равномерно со скоростью 75 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 3 км/ч навстречу поезду, за 30 секунд. Найдите длину поезда в
метрах.
б) Поезд, двигаясь равномерно со скоростью 46 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4 км/ч навстречу поезду, за 45 секунд. Найдите длину поезда в
метрах.
249. а) Поезд, двигаясь равномерно со скоростью 75 км/ч, проезжает мимо пешехода, идущего в том
же направлении параллельно путям по платформе со скоростью 3 км/ч, за 18 секунд. Найдите
длину поезда в метрах.
б) Поезд, двигаясь равномерно со скоростью 84 км/ч, проезжает мимо пешехода, идущего в том
же направлении параллельно путям по платформе со скоростью 6 км/ч, за 18 секунд. Найдите
длину поезда в метрах.
250. а) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский
и товарный поезда, скорости которых равны соответственно 120 км/ч и 90 км/ч. Длина товарного поезда равна 1900 метрам. Найдите длину пассажирского поезда в метрах, если время, за
которое он прошёл мимо товарного поезда, равно 5 минутам.
б) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский
и товарный поезда, скорости которых равны соответственно 130 км/ч и 80 км/ч. Длина товарного поезда равна 1600 метрам. Найдите длину пассажирского поезда в метрах, если время, за
которое он прошёл мимо товарного поезда, равно 3 минутам.
Задачи на движение по воде
251. а) Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки
в стоячей воде в км/ч, если скорость течения реки равна 3 км/ч.
49
б) Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки
в неподвижной воде в км/ч, если скорость течения реки равна 4 км/ч.
252. а) Баржа прошла по течению реки 45 км и, повернув обратно, прошла ещё 42 км, затратив на
весь путь 6 часов. Найдите собственную скорость баржи в км/ч, если скорость течения реки
равна 3 км/ч.
б) Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 36 км, затратив на
весь путь 5 часов. Найдите собственную скорость баржи в км/ч, если скорость течения реки
равна 4 км/ч. Ответ дайте в км/ч.
253. а) Расстояние между пристанями А и В равно 70 км. Из А в В по течению реки отправился
плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас
повернула обратно и возвратилась в А. К этому времени плот прошёл 26 км. Найдите скорость
лодки в неподвижной воде в км/ч, если скорость течения реки равна 2 км/ч.
б) Расстояние между пристанями А и В равно 38,5 км. Из А в В по течению реки отправился
плот, а через час вслед за ним отправился катер, которая, прибыв в пункт В, тотчас повернул
обратно и возвратился в А. К этому времени плот прошёл 22 км. Найдите скорость катера в
неподвижной воде в км/ч, если скорость течения реки равна 4 км/ч.
254. а) Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде в км/ч, если скорость
течения равна 4 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается
через 28 часов после отплытия из него.
б) Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в стоячей воде в км/ч, если скорость
течения равна 5 км/ч, стоянка длится 12 часа, а в пункт отправления теплоход возвращается
через 24 часа после отплытия из него.
255. а) Катер тратит на путь от пункта А до пункта В, расположенного ниже по течению реки, такое же время, как на путь от пункта В до пункта С, расположенного посередине между А и В.
Найдите отношение скорости катера в стоячей воде к скорости течения реки.
б) Катер и теплоход следуют по одному маршруту против течения реки. В стоячей воде скорость
катера в 4 раза больше скорости теплохода, а на весь маршрут он тратит в 5 раз меньше времени,
чем теплоход. Найдите отношение скорости теплохода в стоячей воде к скорости течения реки.
Задачи на среднюю скорость
256. а) Первые 3 часа автомобиль ехал со скоростью 60 км/ч, следующие 2 часа – со скоростью
75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути в км/ч.
б) Первые 2 часа автомобиль ехал со скоростью 75 км/ч, следующие 4 часа – со скоростью
45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути в км/ч.
257. а) Первую половину пути автомобиль проехал со скоростью 54 км/ч, а вторую – со скоростью
90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути в км/ч.
б) Первую половину пути автомобиль проехал со скоростью 84 км/ч, а вторую – со скоростью
96 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути в км/ч.
258. а) Первые 180 км автомобиль ехал со скоростью 60 км/ч, следующие 210 км – со скоростью
105 км/ч, а последние 150 км – со скоростью 50 км/ч. Найдите среднюю скорость автомобиля
на протяжении всего пути в км/ч.
50
б) Первые 250 км автомобиль ехал со скоростью 125 км/ч, следующие 170 км – со скоростью
85 км/ч, а последние 120 км – со скоростью 60 км/ч. Найдите среднюю скорость автомобиля
на протяжении всего пути в км/ч.
Задачи на работу
259. а) Два мастера по ремонту, работая отдельно, могут покрасить стену за 4 и 6 часов соответственно. За сколько часов они покрасят ее, работая вместе?
б) Первый экскаватор может выкопать котлован за 36 часов, а второй может выкопать тот же
котлован за 18 часов. За сколько часов этот котлован выкопают оба экскаватора, работая вместе?
260. а) На обработку одной детали первый рабочий затрачивает на 5 минут меньше, чем второй.
Сколько деталей обрабатывает второй рабочий за 5 часов, если первый за это время обрабатывает на 3 детали больше другого?
б) На обработку одной детали первый рабочий затрачивает на 10 минут меньше, чем второй.
Сколько деталей обрабатывает первый рабочий за 9 часов, если второй за это время обрабатывает на 9 деталей меньше другого?
261. а) Первый рабочий за час делает на 13 деталей больше, чем второй, и выполняет заказ, состоящий из 234 деталей, на 9 часов быстрее, чем второй рабочий, выполняющий такой же заказ.
Сколько деталей в час делает второй рабочий?
б) Первый рабочий за час делает на 9 деталей меньше, чем второй, и выполняет заказ, состоящий из 216 деталей, на 4 часа медленнее, чем второй рабочий, выполняющий такой же заказ.
Сколько деталей в час делает первый рабочий?
262. а) Работая вместе, двое рабочих, выполнили заказ за 4 часа 48 минут. Известно, что первый
рабочий, работая в одиночку, выполняет такой же заказ на 4 часа быстрее, чем его выполнит
второй рабочий, также работая в одиночку. За сколько часов выполнит эту работу первый рабочий?
б) Работая вместе, двое рабочих, выполнили заказ за 7 часов 12 минут. Известно, что первый
рабочий, работая в одиночку, выполняет такой же заказ на 6 часов быстрее, чем его выполнит второй рабочий, также работая в одиночку. За сколько часов выполнит эту работу первый рабочий?
263. а) Бассейн может наполняться через две трубы. Если открыть только первую, то бассейн наполнится за 40 минут. Если же открыть только вторую, то за 60 минут соответственно. Через
сколько минут наполнится бассейн, если открыть одновременно обе трубы?
б) Две трубы наполняют бассейн за 3 часа 9 минут, а одна первая труба наполняет бассейн за
4 часа 30 минут. За сколько часов наполняет бассейн одна вторая труба?
264. а) Две трубы, работая одновременно, наполняют бочку за 12 минут. Первая труба наполняет
бочку на 10 минут быстрее второй. За сколько минут наполняет бочку вторая труба?
б) Две трубы, работая одновременно, наполняют бочку за 4 минуты. Первая труба наполняет
бочку на 6 мин дольше, чем вторая труба. За сколько минут наполняет бочку только вторая труба?
265. а) Из первой трубы за 7 минут вытекает воды на 1,75 литра больше, чем из второй, а бак объёмом 300 л наполняется второй трубой на 1 час медленнее, чем первой. Сколько литров воды
вытекает за час из второй трубы?
б) Из первой трубы за 6 минут вытекает на 18 литров воды меньше, чем из второй, а бак объёмом 260 л наполняется второй трубой на 6 минут быстрее, чем первой. Сколько литров воды
в минуту пропускает вторая труба?
51
266. а) Бассейн может наполняться через три трубы. Если будут открыты первая и вторая трубы,
бассейн наполнится за 9 часов. Если открыты вторая и третья – за 12 часов, а если открыты
первая и третья – за 18 часов. За сколько часов наполнится бассейн, если будут отрыты все три
трубы?
б) Бассейн может наполняться через три трубы. Если будут открыты первая и вторая трубы,
бассейн наполнится за 18 часов. Если открыты вторая и третья – за 20 часов, а если открыты
первая и третья – за 30 часов. За сколько часов наполнится бассейн, если будут отрыты все
три трубы?
Задачи на проценты
267. а) Свежие фрукты содержат 76% воды, а сухие – 4% воды. Сколько килограммов сухих фруктов
получится из 32 кг свежих фруктов?
б) Свежие фрукты содержат 82% воды, а высушенные – 28%. Сколько килограммов сухих фруктов получится из 48 кг свежих фруктов?
268. а) Свежие фрукты содержат 80% воды, а высушенные – 10%. Сколько килограммов свежих
фруктов надо взять, чтобы получилось 12 кг сухих фруктов?
б) Свежие фрукты содержат 82% воды, а высушенные – 19%. Сколько килограммов свежих
фруктов надо взять, чтобы получилось 16 кг сухих фруктов?
269. а) Смешали 4 литра 5-процентного раствора кислоты с 6 литрами 10-процентного раствора этой
же кислоты. Определите процентную концентрацию получившегося раствора.
б) Смешали 2 литра 15-процентного раствора кислоты с 8 литрами 20-процентного раствора
этой же кислоты. Определите процентную концентрацию получившегося раствора.
270. а) Первый сплав содержит 25% меди, второй – 30% меди. Масса второго сплава больше массы
первого на 5 кг. Сплавив эти два сплава, получили сплав, содержащий 28% меди. Найдите массу
получившегося сплава в килограммах.
б) Первый сплав содержит 20% меди, второй – 40% меди. Масса второго сплава больше массы
первого на 6 кг. Сплавив эти два сплава, получили сплав, содержащий 33% меди. Найдите массу
получившегося сплава в килограммах.
271. а) Сплав меди и цинка весом 70 кг содержит 50% меди. Сколько килограммов цинка нужно
добавить, чтобы в сплаве его концентрация достигла 60%?
б) Сплав меди и цинка весом 40 кг содержит 30% меди. Сколько килограммов цинка нужно
добавить, чтобы в сплаве его концентрация достигла 50%?
272. а) Имеется два сплава с разным содержанием золота: в первом содержится 70%, а во втором –
45% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них
новый сплав, содержащий 50% золота?
б) Имеется два сплава с разным содержанием золота: в первом содержится 90%, а во втором –
65% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них
новый сплав, содержащий 75% золота?
52
Проверочная работа № 13
Вариант 1
1. И
меется два раствора кислоты с концентрациями 50% и 45%. Если их слить в один сосуд,
получится раствор массой 4 кг, содержащий 48% кислоты. Найдите массу второго раствора в
килограммах.
ервые 150 км автомобиль ехал со скоростью 75 км/ч, следующие 255 км – со скоростью
2. П
85 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути в км/ч.
асстояние между пристанями А и В равно 38,5 км. Из А в В по течению реки отправился плот,
3. Р
а через час вслед за ним отправился катер, которая, прибыв в пункт В, тотчас повернул обратно
и возвратился в А. К этому времени плот прошёл 22 км. Найдите скорость катера в стоячей воде
в км/ч, если скорость течения реки равна 4 км/ч.
оезд, двигаясь равномерно со скоростью 78 км/ч, проезжает мимо пешехода, идущего парал4. П
лельно путям со скоростью 3 км/ч навстречу поезду, за 20 секунд. Найдите длину поезда в метрах.
ервый рабочий за час делает на 8 деталей больше, чем второй, и выполняет заказ, состоящий
5. П
из 270 деталей, на 12 часов быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько
деталей в час делает второй рабочий?
Вариант 2
меется два раствора кислоты с концентрациями 80% и 40%. Если их слить в один сосуд,
1. И
получится раствор массой 5 кг, содержащий 72% кислоты. Найдите массу второго раствора
в килограммах.
ервые 240 км автомобиль ехал со скоростью 80 км/ч, следующие 285 км – со скоростью
2. П
95 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути в км/ч.
асстояние между пристанями А и В равно 88 км. Из А в В по течению реки отправился плот,
3. Р
а через час вслед за ним отправился катер, которая, прибыв в пункт В, тотчас повернул обратно
и возвратился в А. К этому времени плот прошёл 31,5 км. Найдите скорость катера в стоячей
воде в км/ч, если скорость течения реки равна 3 км/ч.
оезд, двигаясь равномерно со скоростью 85 км/ч, проезжает мимо пешехода, идущего парал4. П
лельно путям со скоростью 4 км/ч в том же направлении, за 24 секунд. Найдите длину поезда
в метрах.
ервый рабочий за час делает на 4 детали больше, чем второй, и выполняет заказ, состоящий
5. П
из 330 деталей, на 8 часов быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько
деталей в час делает второй рабочий?
4.7. Анализ утверждений
273. Петр старше Василия, но младше Дениса. Алексей не старше Петра. Выберите утверждения,
которые верны при указанных данных. В ответе запишите номера выбранных утверждений без
пробелов и запятых.
1)
2)
3)
4)
Денис самый старший среди всех указанных людей.
Денис и Алексей одногодки.
Петр и Василий одногодки.
Василий младше Дениса.
53
274. В волейбольной команде измерили рост всех игроков для сбора статистики. Оказалось, что рост
любого спортсмена команды больше 185 см и меньше 200 см. Выберите утверждения, которые
верны при указанных данных. В ответе запишите номера выбранных утверждений без пробелов
и запятых.
1)
2)
3)
4)
В указанной команде есть спортсмен, рост которого 200 см.
В указанной команде нет спортсмена, рост которого 180 см.
Рост любого спортсмена меньше 200 см.
Разница в росте двух любых спортсменов указанной команды составляет менее 15 см.
275. Десять учеников из 11 класса сдавали ЕГЭ по математике. В итоге оказалось, что среди этих
учеников самый низкий результат – 40 баллов, а самый высокий – 95 баллов. Выберите утверждения, которые верны при указанных данных. В ответе запишите номера выбранных утверждений
без пробелов и запятых.
1)
2)
3)
4)
Среди этих учеников есть выпускник, который получил 95 баллов за ЕГЭ по математике.
Среди этих учеников есть хотя бы двое с одинаковыми баллами за ЕГЭ по математике.
Среди этих учеников есть выпускник, получивший 50 баллов за ЕГЭ по математике.
Баллы за ЕГЭ по математике любого из этих учеников не ниже 40.
276. В книжном шкафу 15 книг. Толщина каждой книги меньше 20 миллиметров, но не меньше
10 миллиметров. Выберите утверждения, которые верны при указанных данных. В ответе запишите номера выбранных утверждений без пробелов и запятых.
1)
2)
3)
4)
В шкафу есть книга толщиной 20 миллиметров.
Найдётся две книги, разница в толщине которых больше 5 миллиметров.
В шкафу нет книги толщиной 5 миллиметров.
Толщина любой книги в шкафу больше 9 миллиметров.
277. В инженерном 11-ом классе школы урок по углубленной математике по расписанию по вторникам и пятницам. Каждый ученик должен носить задачник по математике только если есть урок
по углубленной математике. Выберите утверждения, которые верны при указанных данных. В
ответе запишите номера выбранных утверждений без пробелов и запятых.
1) Всякий день, когда ученик берёт с собой в школу задачник по математике, является пятницей.
2) Во вторник ученику из инженерного класса надо принести задачник по математике.
3) По четвергам ученикам инженерного класса не надо брать в школу задачник по математике.
4) В любой день, кроме вторника, ученикам инженерного класса можно не брать в школу задачник по математике.
278. Фирма отправила несколько своих сотрудников на курсы повышения квалификации по специальности «А». Через некоторое время фирма решила, что необходимо отправить ещё несколько
сотрудников на стажировку по специальности «Б», причём среди них не будет тех, кто ездил на
курсы по специальности «А». Выберите утверждения, которые верны при указанных данных. В
ответе запишите номера выбранных утверждений без пробелов и запятых.
1) Найдется сотрудник, который ездил на курсы по специальности «А» и не поедет на курсы
по специальности «Б».
2) Среди сотрудников, которые не поедут на курсы по специальности «Б», есть хотя бы один,
который был на курсах по специальности «А».
3) Каждый сотрудник, который был на курсах по специальности «А», поедет на курсы по специальности «Б».
54
4) Нет ни одного сотрудника, который ездил на курсы по специальности «А» и поедет на курсы
по специальности «Б».
279. На столе стоят 15 тарелок с салатом. В семи из них салат заправлен майонезом, а в остальных –
майонеза нет. В пять тарелок повар добавил зелень. Выберите утверждения, которые верны при
указанных данных. В ответе запишите номера выбранных утверждений без пробелов и запятых.
1)
2)
3)
4)
Хотя бы в 4 тарелках есть зелень, но нет майонеза.
Хотя бы в 3 тарелках нет ни майонеза, ни зелени.
Если в тарелке нет майонеза, то там есть зелень.
Не найдётся 7 тарелок без майонеза, но с зеленью.
280. На экскурсию поехало 25 человек. Из них 17 человек посетили музей космонавтики, а 12 – музей истории. Каждый экскурсант посетил хотя бы один музей. Выберите утверждения, которые
верны при указанных данных. В ответе запишите номера выбранных утверждений без пробелов
и запятых.
1)
2)
3)
4)
Каждый экскурсант посетил оба музея.
Найдётся хотя бы четыре экскурсанта, которые посетили оба музея.
Если экскурсант посетил музей космонавтики, то он обязательно посетил и музей истории.
Не найдётся 5 экскурсантов, которые посетили бы оба музея.
281. В школе учится 120 школьников. Из них 100 школьников знают английский язык, а 30 школьников знают немецкий язык. Выберите утверждения, которые верны при указанных данных. В
ответе запишите номера выбранных утверждений без пробелов и запятых.
1)
2)
3)
4)
Если школьник знает английский язык, то он знает и немецкий.
Есть хотя бы пять школьников, которые знают оба языка.
Не более 30 школьников знают оба языка.
В школе нет ребят, которые не знают ни одного иностранного языка.
282. На олимпиаде по математике участники решали задачи. Участник «А» решил задач больше,
чем участник «Б» и участник «В» вместе взятые. Участник «Г» и участник «Б» вместе решили
больше задач, чем участник «А». Участник «В» и участник «А» вместе решили больше задач,
чем участник «Г» и участник «Б» вместе взятые. Выберите утверждения, которые верны при
указанных данных. В ответе запишите номера выбранных утверждений без пробелов и запятых.
1)
2)
3)
4)
Участник
Участник
Участник
Участник
«Г» решил больше задач, чем участник «В».
«Б» и участник «В» вместе решили больше задач, чем участник «А».
«А» решил больше задач, чем участник «Б».
«А» решил больше задач, чем участник «Г».
283. Некоторые учителя школы летом работали экспертами по проверке ЕГЭ, а некоторые – ездили
на море. Те учителя, кто ездил на море, не работали экспертами по проверке ЕГЭ. Выберите
утверждения, которые верны при указанных данных. В ответе запишите номера выбранных
утверждений без пробелов и запятых.
1)
2)
3)
4)
Каждый учитель школы работал экспертом по проверке ЕГЭ.
Если учитель работал экспертом по проверке ЕГЭ, то он не ездил на море.
Нет ни одного учителя, который летом работал экспертом по проверке ЕГЭ и ездил на море.
Среди учителей, которые не ездили на море, есть хотя бы один эксперт по проверке ЕГЭ.
284. Когда рабочий находится на стройплощадке, то он обязательно надевает каску. Выберите утверждения, которые верны при указанных данных. В ответе запишите номера выбранных утверждений
без пробелов и запятых.
55
1)
2)
3)
4)
Если
Если
Если
Если
рабочий
рабочий
рабочий
рабочий
в каске, значит, он находится на стройплощадке.
находится на стройплощадке, значит, он без каски.
находится на стройплощадке, значит, он в каске.
без каски, значит, он не находится на стройплощадке.
285. Смартфон дороже наушников. Часы дороже планшета. Планшет стоит больше, чем смартфон
и наушники вместе взятые. Выберите утверждения, которые верны при указанных данных. В
ответе запишите номера выбранных утверждений без пробелов и запятых.
1) Самый дорогой из четырех гаджетов – планшет.
2) Смартфон и наушники вместе стоят дороже, чем часы.
3) Планшет дороже смартфона.
4) Нельзя определить, какой из четырёх гаджетов самый дорогой.
286. Известно, что все виды форели – рыбы, а все рыбы плавают в воде. Дельфины также плавают в
воде. Выберите утверждения, которые верны при указанных данных. В ответе запишите номера
выбранных утверждений без пробелов и запятых.
1)
2)
3)
4)
Все дельфины – рыбы.
Если животное не плавает, то это не дельфин.
Все виды форели плавают в воде.
Если животное плавает в воде, то оно либо форель, либо дельфин.
287. Как известно, в жилых домах, в которых больше 5 этажей обязательно устанавливают лифт.
Выберите утверждения, которые верны при указанных данных. В ответе запишите номера выбранных утверждений без пробелов и запятых.
1)
2)
3)
4)
Если
Если
Если
Если
в
в
в
в
доме
доме
доме
доме
нет лифта, то в этом доме больше 6 этажей.
нет лифта, то в этом доме меньше 6 этажей.
меньше 6 этажей, то в нём нет лифта.
больше 6 этажей, то в нём есть лифт.
288. Если треугольник прямоугольный, то какие-то из его сторон являются высотами. Выберите утверждения, которые верны при указанных данных. В ответе запишите номера выбранных утверждений без пробелов и запятых.
1) В любом треугольнике одна из сторон является высотой.
2) Если в треугольнике две стороны являются высотами, то он прямоугольный.
3) Если ни одна из сторон не является высотой треугольника, то такой треугольник не прямоугольный.
4) Если высота перпендикулярна стороне треугольника, то такой треугольник прямоугольный.
289. В некоторый день цена на акции компании А составила 6 условных единиц. В тот же день цена
на акции компании Б стала на 5 условных единиц меньше, чем цена на акции компании А, а
цена на акции компании В стала на 5 условных единиц больше, чем цена на акции компании
А. Выберите утверждения, которые верны при указанных данных. В ответе запишите номера
выбранных утверждений без пробелов и запятых.
1)
2)
3)
4)
56
Акции компании А дешевле, чем акции компании В в указанный день.
В указанный день цена на акции компании В выше, чем цена на акции компании Б.
В указанный день акции компании Г дороже акций компании А.
Акции компании А всегда дороже акций компании Б.
Проверочная работа № 14
Вариант 1
Школьник часто ездит в школу на самокате. Он не ездит на самокате в те дни, когда плохая погода, а также по пятницам, когда сразу после уроков уезжает с родителями на дачу. Выберите
утверждения, которые верны при указанных данных. В ответе запишите номера выбранных утверждений без пробелов и запятых.
1) Каждый день, когда хорошая погода, школьник будет ехать в школу на самокате.
2) Сегодня школьник приехал в школу на самокате, значит сегодня нет дождя.
3) Каждый день, когда школьник приходит в школу пешком, он едет после уроков на дачу.
4) Не менее одного дня в неделю школьник ходит пешком в школу.
Вариант 2
За городом расположен торговый центр. Администрация торгового центра организовала бесплатную перевозку от торгового центра до города с использованием автобусов. Если в автобусе заняты
все места, то он трогается от остановки и едет в город. Выберите утверждения, которые верны при
указанных данных. В ответе запишите номера выбранных утверждений без пробелов и запятых.
1) Если в автобусе есть свободные места, то он не трогается.
2) Если автобус стоит на остановке, то в нем есть свободные места.
3) Если автобус отъехал от остановки, то в нем заняты все места.
4) Если на каждом месте сидит школьник, то автобус трогается от остановки.
4.8. Задачи на смекалку
290. На деревянной доске по разные стороны от середины отмечены карандашом две поперечные
полосы: левая и правая. Если разрезать доску по левой полоске, то одна часть доски будет на
30 см длиннее другой. Если разрезать доску по правой полоске, то одна часть будет на 40 см
длиннее другой. Найдите расстояние (в сантиметрах) между полосками.
291. На деревянной доске отмечены поперечные полоски красного, синего и зелёного цветов. Полоски не совпадают друг с другом. Если распилить доску по красным полоскам, получится
10 кусков, если распилить по синим – 7 кусков, если по зелёным – 5 кусков. Сколько кусков
получится, если распилить доску по полоскам всех цветов?
292. Десять домов соединены между собой оптическим волокном. Каждый дом соединен кабелем с
любым другим. Сколько отрезков кабелей соединяют дома между собой?
293. Двадцать домов соединены между собой проводами таким образом, что от каждого дома отходит
пять проводов. Сколько всего отрезков проводов соединяют все дома?
294. В вазе лежит 40 фруктов: яблоки и груши. Известно, что среди любых 17 фруктов имеется хотя
бы одно яблоко, а среди любых 25 фруктов хотя бы один груша. Сколько яблок в вазе?
295. Александр пригласил Михаила в гости, сообщив, что живёт в 172 квартире, но Михаил забыл
спросить, на каком этаже живет Александр. Подойдя к дому, Михаил увидел, что дом 14-этажный
и в нём 4 подъезда. Количество квартир на каждом этаже одинаковое. На каком этаже живёт
Александр?
57
296. Жук способен перемещается вдоль координатной прямой в обоих направлениях на единичный
отрезок за один ход. В скольких различных точках может оказаться жук, сделав ровно 10 ходов,
стартуя из начала координат?
297. Жук за один ход заползает вверх по доске на 2 метра, но затем скатывается вниз на 1 м. За
сколько ходов жук впервые окажется на высоте 8 метров?
298. Три игрока играют в настольный теннис: игрок, проигравший партию, уступает место игроку,
не участвовавшему в ней. В итоге оказалось, что первый игрок сыграл 12 партий, второй – 25.
Сколько партий сыграл третий игрок?
299. В сосуд поместили одну бактерию. Оказалось, что за одну секунду каждая бактерия делится
на две новые бактерии, а сосуд наполняется бактериями за 1 минуту.. За сколько секунд сосуд
будет заполнен бактериями наполовину?
300. Среднее арифметическое пяти различных натуральных чисел равно 10. Среднее арифметическое
этих чисел и шестого числа равно 14. Найдите шестое число.
301. В результате наводнения подвал дома заполнился водой до уровня 1,5 метров. Спасатели откачивают воду, понижая её уровень на 15 см в час. Однако, прибывающая вода продолжать повышать уровень воды на 5 см в час. За сколько часов работы спасателей, уровень воды в подвале
снизится до 50 см?
302. В жилом доме в каждом подъезде одинаковое число квартир на каждом этаже и одинаковое
число этажей. Известно, что число подъездов больше одного, число этажей в подъезде больше
количества квартир на одном этаже, а количество квартир на этаже больше числа подъездов.
Сколько этажей в доме, если всего в нем 273 квартиры?
303. Произведение пятнадцати идущих подряд натуральных чисел разделили на 13. Чему равен остаток от деления?
304. В конце триместра ученик выписал в ряд все свои отметки по литературе, их оказалось пять
штук, и поставил между некоторыми из них знаки умножения. А затем перемножил получившиеся числа. Произведение оказалось равным 954. Какую отметку по литературе получит ученик за указанный триместр, если отметка в триместре получается в результате округления по
правилам математического округления среднего арифметического всех отметок за триместр, а
отметок кроме 2, 3, 4 и 5 не ставят?
305. В новом доме Сергея 12 запертых дверей и ему передали 12 ключей от этих дверей. Каждая
дверь открывается только одним ключом, но Сергей не знает, какой ключ подходит к той или
иной двери. Первую дверь он пробует открыть каждым из 12 ключей. Если выбранный ключ
подходит к двери, то эта попытка открыть дверь считается удачной. Какое наибольшее количество неудачных попыток может сделать Сергей при открывании всех дверей одной за другой?
306. В шахматном турнире принимали участие 12 шахматистов, причем каждый из них сыграл только
одну партию с каждым другим шахматистом. Сколько всего партий было сыграно в турнире?
58
307. На окружности отмечено 5 точек. Сколько можно нарисовать треугольников с вершинами в этих точках?
308. Сколько различных дробей можно составить из 6 первых простых чисел так, чтобы в каждую
дробь входили 2 различных числа?
309. Сколько способов существует для расстановки в ряд трёх белых ваз, двух жёлтых ваз и одной
синей вазы, если все вазы различаются только цветом?
310. 35 человек приняли участия в социологическом опросе. В ходе опроса им задали три вопроса:
«Бывали ли Вы на море?», «Бывали ли Вы в горах?», «Бывали ли Вы в пустыне?». Итоги опроса
оказались следующими: на море и в горах побывало 9 человек, в горах и пустыне – 4 человека, а на море и в пустыне – 1. Пять человек не бывали ни на море, ни в горах, ни в пустыне.
Восемнадцать человек ответили утвердительно только на один из перечисленных вопросов.
Сколько человек посещали природные объекты ровно двух видов?
311. В классе каждый ученик сдает по выбору ЕГЭ хотя бы по одному из следующих предметов:
информатика, химия, физика. Известно, что ЕГЭ по информатике или химии сдают 28 человек,
по информатике или физике – 26, по химии или физике – 24. Одновременно информатику и
химию сдают 5 учащихся, информатику и физику – 7, химию и физику – 6. Экзамен по всем
трём предметам сдают 2 человека. Сколько всего человек в классе?
312. Круизный лайнер проходит расстояние между портами «А» и «Б» за 12 суток. Ежедневно одним
и тем же маршрутом как из порта «А» в порт «Б», так и из порта «Б» в порт «А» отправляется
по одному судну. Сколько судов встречает за время плавания из одного порта в другой каждое
плывущее судно без учета встречающихся в порту, если все суда выходят из порта и прибывают
в порт в одно и тоже время?
313. При подготовке к ЕГЭ по математике выяснилось, что среди 24 учеников 11 класса 5 учеников
пишут тренировочную работу всегда только на 5, 15 учеников – на 4 или 5, а 4 ученика могут
получить за работу на 3, 4 или 5. Сколько учеников из этого класса достаточно посадить в
аудиторию, чтобы наверняка хотя бы одна из работ, написанных ими в этой аудитории, была
оценена оценкой 5?
314. На гору высотой 500 метров поднимается скалолаз. Сначала он преодолел 50 метров за 10 минут,
а каждый следующий отрезок пути длиной 50 метров преодолевал на 2 минуты дольше, чем
предыдущий. На вершине скалолаз отдыхал в течение 40 минут, затем начал спуск со скоростью
5 м/мин. Через сколько минут после начала подъёма скалолаз вновь окажется у подножия горы?
315. Каждое из чисел 1, 2, 3, 4, 5 умножают на каждое из чисел 6, 7, 8, 9. Перед каждым полученным
произведением ставят плюс или минус, и затем складывают все 20 полученных результатов.
Какую наибольшую сумму можно получить в итоге?
59
§ 5. Анализ диаграмм и графиков
316. На диаграмме по данным аналитического агентства представлена динамика количества продаж
новых автомобилей в России в период с 2002 г. по 2017 г. По вертикали указано количество
проданных автомобилей в тысячах штук, а по горизонтали – годы продаж.
3200
3200
3000
2920
2800
2800
2650
2600
3010
2800
2780
2600
2450
2400
2200
2000
1900
1900
1800
1550
1600
1400
1200
1200
1300
1400
1450
1000
800
2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017
Укажите в ответе разницу между наибольшим и наименьшим значениями продаж по годам
(ответ запишите в тыс. штук).
317. Используя условие и диаграмму, представленные в задании 316, найдите, во сколько раз больше
продано автомобилей в год с наибольшим значением продаж, чем в год с наименьшим таким
значением. Результат округлите до десятых..
318. Используя условие и диаграмму, представленные в задании 316, найдите, через сколько лет
впервые количество проданных автомобилей увеличилось более чем в 2 раза в сравнении с
2002 годом.
319. На диаграмме по данным аналитического агентства представлена динамика количества продаж
автомобилей в России в период с 2006 г. по 2020 г. По вертикали указано количество проданных
автомобилей в штуках, а по горизонтали – годы продаж.
3 000000
2500000
2000000
1500000
1000000
500000
0
2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020
Укажите в ответе количество лет, в которые продажа превышала 2 млн автомобилей.
60
320. Используя условие и диаграмму, представленные в задании 319, укажите в ответе количество
лет, в которые продажа не превышала 1,5 млн автомобилей.
321. На диаграмме показана среднемесячная температура днем в г. Москве с января по декабрь
2022 года. По вертикали указана температура в градусах Цельсия, а по горизонтали – название
месяца.
25
20
15
10
5
0
–5
–10
январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
Определите по диаграмме наименьшую среднемесячную температуру в городе в течение года.
Ответ дайте в градусах Цельсия.
322. Используя условие и диаграмму, представленные в задании 321, укажите в ответе количество
месяцев, в которые среднемесячная температура была положительна.
323. Используя условие и диаграмму, представленные в задании 321, укажите в ответе перепад температур в течение года (то есть разницу между наибольшим и наименьшим значениями). Ответ
дайте в градусах Цельсия.
324. На диаграмме показано количество солнечных дней в г. Москве с января по декабрь 2022 года.
По вертикали указано количество дней, а по горизонтали – название месяца.
8
7
6
5
4
3
2
1
0
январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
Определите по диаграмме суммарное количество солнечных дней в третьем квартале года.
325. Используя условие и диаграмму, представленные в задании 324, укажите в ответе порядковый
номер месяца в году, в котором было минимальное количество солнечных дней.
326. На диаграмме представлено суммарное количества осадков, выпадавших каждый месяц в некотором городе с января по декабрь. По вертикали указано количество осадков в миллиметрах,
а по горизонтали – названия месяцев.
61
30
25
20
15
10
5
0
январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
Определите по диаграмме разницу между наибольшим и наименьшим месячными показателями
количества выпавших осадков за весь год. Ответ дайте в миллиметрах.
327. Используя условие и диаграмму, представленные в задании 326, укажите в ответе общее количество осадков, выпавших в четвертом квартале года. Ответ дайте в миллиметрах.
328. На диаграмме показана среднемесячная температура в некотором городе с января по декабрь.
По вертикали указана температура в градусах Цельсия, а по горизонтали – номер месяца.
t°C
24
21
18
15
12
9
6
3
0
–3
–6
–9
–12
–15
–18
–21
1 2 3 4 5 6 7 8 9 10 11 12 номер
месяца
Определите по диаграмме наименьшую среднемесячную температуру в рассматриваемом городе
в течение года. Ответ дайте в градусах Цельсия.
329. Используя условие и диаграмму, представленные в задании 328, укажите наименьшую среднемесячную температуру в рассматриваемом городе в третьем квартале года. Ответ дайте в градусах
Цельсия.
330. Используя условие и диаграмму, представленные в задании 328, укажите в ответе перепад среднемесячных температур в первом квартале (то есть разницу между наибольшим и наименьшим
значениями). Ответ дайте в градусах Цельсия.
62
331. На диаграмме показано количество финишеров (то есть преодолевших дистанцию) на марафоне, состоявшемся 20 сентября 2020 года в г. Москве, в мужских и женских возрастных группах
(1-я группа – 18-19 лет; 2-я – 20-22 года; 3-я – 23-29 лет; 4-я – 30-34 года; 5-я – 35-39 лет ; 6-я –
40-44 года; 7-я – 45-49 лет; 8-я – 50-54 года; 9-я – 55-59 лет; 10-я – 60-64 года: 11-я – 65-69 лет;
12-я – 70-74 года; 13-я – 75-79 лет; 14-я – 80-120 лет). По вертикали указано количество человек,
а по горизонтали – номера возрастных групп.
2000
Мужчины
Женщины
1000
800
400
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Определите по диаграмме номера групп, в которых разница между количеством финишировавших
мужчин и женщин составила не менее 500 человек. В ответе укажите номера этих групп без
пробелов и запятых в порядке возрастания.
332. На графике изображена зависимость скорости движения тела от времени. На вертикальной оси
отмечена скорость движения тела в м/c, на горизонтальной – время в секундах, прошедшее от
начала движения. Пользуясь графиком, поставьте в соответствие каждому интервалу времени
характеристику движения тела на этом интервале.
v, м/с
8
7
6
5
4
3
2
1
0
2
ИНТЕРВАЛЫ ВРЕМЕНИ
А) 4-8 секунд
Б) 8-12 секунд
В) 12-16 секунд
Г) 18-22 секунд
4
6
8
10
12
14
16
18
20
22
t, с
ХАРАКТЕРИСТИКИ
1) тело не двигалось 2 секунды
2) скорость тела была не меньше 1 м/c на всём интервале
3) скорость тела была не больше 6 м/c на всём интервале
4) тело сделало остановку длительностью ровно 1 секунда
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
63
333. На графике изображена зависимость скорости движения тела от времени. На вертикальной оси
отмечена скорость тела в м/с, на горизонтальной – время в секундах, отсчитываемое от начала
движения тела. Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения тела на этом интервале.
v, м/с
80
60
40
20
0
15
30
ИНТЕРВАЛЫ ВРЕМЕНИ
А) 0-30 секунд
Б) 60-90 секунд
В) 90-120 секунд
Г) 120-150 секунд
45
60
75
90 105 120 135 150
t, с
ХАРАКТЕРИСТИКИ
1) скорость тела сначала увеличивалась, а затем уменьшалась
2) тело более 15 секунд двигалось с постоянной скоростью
3) тело не двигалось 15 секунд
4) скорость тела росла на всём интервале
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
334. На графике изображена зависимость скорости движения автомобиля от времени. На вертикальной оси отмечена скорость тела в км/ч, на горизонтальной – время в минутах, отсчитываемое
от начала движения тела. Пользуясь графиком, поставьте в соответствие каждому интервалу
времени характеристику движения тела на этом интервале.
v, км/ч
80
60
40
20
0
2
ИНТЕРВАЛЫ ВРЕМЕНИ
А) 4-8 минут
Б) 8-12 минут
В) 12-16 минут
Г) 16-20 минут
64
4
6
8
10
12
14
16
18
20
22
t, мин
ХАРАКТЕРИСТИКИ
1) автомобиль сделал остановку длительностью ровно 1 минута
2) автомобиль не сбавлял скорость
3) автомобиль не увеличивал скорость на интервале
4) автомобиль сделал остановку длительностью 2 минуты
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
335. Океанолог исследует структуру поверхности океана с помощью специального датчика. На графике изображена скорость погружения датчика в воду от времени. На вертикальной оси отмечена
скорость погружения датчика в воду в м/c, на горизонтальной – время в секундах, прошедшее с
начала погружения. Пользуясь графиком, поставьте в соответствие каждому интервалу времени
характеристику движения датчика на этом интервале.
v, м/с
0,4
0,3
0,2
0,1
0
60
ИНТЕРВАЛЫ ВРЕМЕНИ
А) 60-120 секунд
Б) 120-180 секунд
В) 180-240 секунд
Г) 240-300 секунд
120
180
240
300
t, с
ХАРАКТЕРИСТИКИ
1) датчик ровно 15 секунд оставался на одной глубине
2) скорость погружения датчика не росла на всём интервале
3) датчик 15 секунд погружался с постоянной скоростью
4) скорость погружения датчика росла на всём интервале
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
336. На рисунке точками показана стоимость акций двух компаний – «А» и «Б» за каждый месяц
года. По вертикали указана стоимость акций в рублях, по горизонтали – месяцы. Для наглядности
точки соединены линиями. Пользуясь рисунком, поставьте в соответствие каждому интервалу
времени характеристику на этом интервале.
130
Акции А
125
Акции Б
120
115
110
105
100
95
90
январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
65
ХАРАКТЕРИСТИКИ
ИНТЕРВАЛЫ ВРЕМЕНИ
А) январь-март
1) стоимость акций «А» в течение 2-ого и 3-его месяцев одинакова
Б) апрель-июнь
2) в течении этого интервала стоимость акций «Б» падала
3) в каждом месяце стоимость акций «Б» выше стоимости акций «А»
В) июль-сентябрь
4) в каждом месяце стоимость акций «А» выше стоимости акций «Б»
Г) октябрь-декабрь
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
337. На рисунке показана среднесуточная температура воздуха в городе за месяц. Для наглядности
точки соединены линиями. По горизонтали указаны числа месяца, по вертикали – температура в
градусах Цельсия. Пользуясь рисунком, поставьте в соответствие каждому интервалу дней месяцев
характеристику на этом интервале.
24
20
16
12
8
4
0
1
3
ИНТЕРВАЛЫ ВРЕМЕНИ
А) 1-7 число
1)
Б) 8-14 число
2)
3)
В) 15-21 число
Г) 22-28 число
4)
5
7
9 11 13 15 17 19 21 23 25 27 29
ХАРАКТЕРИСТИКИ
во второй половине интервала температура не повышалась
температура достигла максимума за месяц
четыре дня интервала значения температуры были одинаковыми
температура не снижалась
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
338. На графике показано изменение атмосферного давления на протяжении трёх первых суток месяца. По горизонтали указывается время измерения и номер дня, по вертикали – давление в
миллиметрах ртутного столба. Пользуясь графиком, поставьте в соответствие каждому интервалу
времени характеристику на этом интервале.
766
764
762
760
758
756
754
752
66
0:00 6:00 12:00 18:00 0:00 6:00 12:00 18:00 0:00 6:00 12:00 18:00 0:00
1 число
2 число
3 число
ИНТЕРВАЛЫ ВРЕМЕНИ
А) 1 число (с 6 до 12 часов)
Б) 2 число (с 6 до 12 часов)
В) 3 число (с 6 до 12 часов)
Г) 3 число (с 12 до 18 часов)
ХАРАКТЕРИСТИКИ
1) давление не менялось и было выше 762 мм. рт. ст.
2) давление увеличивалось
3) давление не менялось и было ниже 762 мм. рт. ст.
4) давление снижалось
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
339. На рисунке точками показано количество участников
олимпиады по математике в зависимости от количества
набранных ими баллов. Для наглядности точки соединены
линиями. На горизонтальной оси отмечено количество набранных баллов, на вертикальной – количество участников, набравших соответствующее число баллов. Пользуясь
графиком, поставьте в соответствие каждому интервалу
баллов характеристику на этом интервале.
ХАРАКТЕРИСТИКИ
1) число участников растёт
2) число участников не меньше 50
3) число участников падает
4) в начале интервала число участников падает, затем растёт
ИНТЕРВАЛЫ
А) 0-3 баллов
Б) 3-6 баллов
В) 6-8 баллов
Г) 8-10 баллов
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
340. На графике показано изменение скорости ветра в зависимости от времени суток. По горизонтали указано
время суток в часах, по вертикали – скорость ветра
в м/с. Пользуясь графиком, поставьте в соответствие
каждому интервалу времени характеристику на этом
интервале.
16
12
8
4
0
ИНТЕРВАЛЫ ВРЕМЕНИ
А) с 0 до 6 часов
Б) с 6 до 12 часов
В) с 12 до 18 часов
Г) с 18 до 24 часов
3
6
9
12
15 18
21 24
ХАРАКТЕРИСТИКИ
1) скорость ветра снижалась
2) скорость ветра была минимальной
3) скорость ветра не опускалась ниже 10 м/с
4) скорость ветра увеличивалась
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
67
341. Из некоторого города выехал автомобиль. На рисунке показано, как менялось расстояние от
автомобиля до города с течением времени. По вертикальной оси указано расстояние от города
до автомобиля в км, по горизонтальной – время в часах, прошедшее с начала движения.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику на
этом интервале.
S, км
80
60
40
20
0
ИНТЕРВАЛЫ А) 1 – 2 часов
Б) 2 – 3 часов
В) 3 – 4 часов
Г) 4 – 5 часов
2
1
0
3
4
t, ч
5
ХАРАКТЕРИСТИКИ
1) в первый раз после начала движения автомобиль вернулся в город
2) автомобиль находился на одном и том же расстоянии от города
3) наименьшее расстояние от автомобиля до города равнялось 30 км
4) расстояние от автомобиля до города было наибольшим
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
342. Установите соответствие между графиками функций и характеристиками этих функций на отрезке [-6; 6].
ГРАФИКИ
ГРАФИКИ
А)
Б)
В)
Г)
Б)
В)
Г)
А)
y
y
y
y
1
1
1
1
0 1
0 1
0 1
x
1)
2)
3)
4)
функция
функция
функция
функция
x
ХАРАКТЕРИСТИКИ
всюду возрастает
всюду убывает
принимает только положительные значения
принимает только отрицательные значения
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
68
А
Б
В
Г
x
0 1
x
343. На рисунке изображен график функции y = f ( x) . Пользуясь графиком, поставьте в соответствие
каждому указанному интервалу соответствующую характеристику функции.
y
a 0
b
c d
e
x
ИНТЕРВАЛЫ
ХАРАКТЕРИСТИКИ
А) (a; b) 1) производная функции положительна в каждой точке
Б) (b; c) 2) производная функции меняет знак с минуса на плюс
В) (c; d ) 3) производная функции отрицательна в каждой точке
Г) (d ; e) 4) интервал содержит точку максимума функции
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
y kx + b . Установите соответствие между гра344. На рисунках изображены графики прямых вида =
фиками и знаками коэффициентов k и b.
ГРАФИКИ
ГРАФИКИ
А)
y
Б)
x
0
y
В)
x
0
y
0
Г)
x
y
0
x
КОЭФФИЦИЕНТЫ
1) k > 0, b > 0
2) k > 0, b < 0
3) k < 0, b > 0
4) k < 0, b < 0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
69
345. На рисунке изображён график функции. Пользуясь графиком, поставьте в соответствие каждой
отмеченной на графике точке соответствующую характеристику функции.
y
A
y = f(x)
B
0
ТОЧКИ
ХАРАКТЕРИСТИКИ
А) А
Б) B
В) C
Г) D
1)
2)
3)
4)
значение
значение
значение
значение
функции
функции
функции
функции
C
D x
положительно, значение производной положительно
отрицательно, значение производной отрицательно
положительно, значение производной отрицательно
отрицательно, значение производной положительно
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
346. На рисунке изображен график функции и касательные к нему в четырёх точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в этой точке.
y
C
B
A
0
y = f(x)
ТОЧКИ
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
А) А
Б) B
В) C
Г) D
1)
2)
3)
4)
−1, 4
0,5
2,5
−0, 2
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
70
А
Б
В
Г
D
x
347. Установите соответствие между функциями в левом столбце и их производными в правом.
ПРОИЗВОДНЫЕ
ФУНКЦИИ
y 5 x + 6 А) =
1) −2
−2 x + 7 Б) y =
2) 3
y 3 x + 2 В) =
3) −10
−10 x + 4 Г) y =
4) 5
В таблице под каждой буквой укажите соответствующий номер.
А
Ответ:
Б
В
Г
348. Установите соответствие между функциями в левом столбце и их производными в правом.
ФУНКЦИИ
y
А) =
ПРОИЗВОДНЫЕ
2
x + 2 3
1) 4
2
3
1
3) −
6
y 4 x + 9 Б) =
2)
−5 x − 7
В) y =
1
6
− x − 6 Г) y =
4) –5
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
А
Б
В
Г
349. Установите соответствие между функциями в левом столбце и значениями их производных в
точке x0 = 1 в правом.
ЗНАЧЕНИЯ ПРОИЗВОДНЫХ В ТОЧКЕ x0 = 1
ФУНКЦИИ
А) y = 3 x 2 + 7 x − 5 1) –1
Б) y = 2 x 2 − 5 x + 3 2) 13
В)=
y 7 x 2 − 3 3) – 4
Г) y =
−3 x 2 + 2 x − 1 4) 14
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
71
350. Установите соответствие между функциями в левом столбце и и значениями их производных в
точке x0 = 1 в правом.
ЗНАЧЕНИЯ ПРОИЗВОДНЫХ В ТОЧКЕ x0 = 1
ФУНКЦИИ
1 2
x + 3 x − 5 2
Б) y = 3 x 2 − 5 x + 3 1
− x2 − 2 x + 1
В) y =
2
Г) y= 4 x 2 − x + 3 А) y =
1) 1
2) 4
3) 7
4) –3
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
351. На рисунке изображены графики функций вида y = ax 2 + bx + c . Установите соответствие между
графиками этих функций и знаками коэффициентов a и c.
ГРАФИКИ
ГРАФИКИ
А)
y
Б)
x
0
y
0
В)
x
y
0
Г)
x
y
0
x
ЗНАКИ КОЭФФИЦИЕНТОВ
2) a > 0, c > 0
1) a < 0, c > 0
3) a > 0, c < 0
4) a < 0, c < 0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
2
352. На рисунке изображены графики функций вида y = ax + bx + c . Установите соответствие между
графиками этих функций и характеристиками коэффициентов a и c.
72
ГРАФИКИ
А)
Б)
y
В)
y
1
1
0 1
y
1
0 1
x
Г)
y
0 1
x
1
x
0 1
x
ХАРАКТЕРИСТИКИ КОЭФФИЦИЕНТОВ
1) a < 0, c =3
2) a > 0, c =−2
3) a < 0, c =4
4) a > 0, c =−5
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
353. На рисунках изображены графики квадратичных функций и графики их производных. Установите
соответствие между графиками функций и графиками их производных.
ГРАФИКИ ФУНКЦИЙ
А)
Б)
y
1
0 1
В)
y
1
0 1
x
Г)
y
y
1
0 1
x
1
0 1
x
x
ГРАФИКИ ПРОИЗВОДНЫХ
1)
2)
y
1
0 1
3)
y
1
x
0 1
4)
y
y
1
x
0 1
1
x
0 1
x
73
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
354. На рисунках изображены графики квадратичных функций и графики их производных. Установите
соответствие между графиками функций и графиками их производных.
ГРАФИКИ ФУНКЦИЙ
А)
Б)
y
В)
y
1
1
0 1
0 1
x
Г)
y
y
1
0 1
x
1
0 1
x
x
ГРАФИКИ ПРОИЗВОДНЫХ
1)
2)
y
3)
y
1
y
1
0 1
0 1
x
4)
1
x
0 1
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
74
А
Б
В
Г
y
1
x
0 1
x
Проверочная работа № 15
Вариант 1
1. На диаграмме показана среднемесячная температура в некотором городе с января по декабрь.
По вертикали указана температура в градусах Цельсия, а по горизонтали – номер месяца.
t°C
24
21
18
15
12
9
6
3
0
–3
–6
–9
–12
–15
–18
–21
1 2 3 4 5 6 7 8 9 10 11 12 номер
месяца
Определите по диаграмме, во сколько раз температура в июле больше, чем температура
в сентябре.
2. На рисунке изображен график функции и касательные в четырёх точках к нему. Установите соответствие между точками и значениями производной в этих точках.
y
D
A
B
0
ТОЧКИ
А) А
Б) B
В) C
Г) D
1)
2)
3)
4)
значение
значение
значение
значение
C
y = f(x)
x
ЗНАЧЕНИЕ ПРОИЗВОДНОЙ
производной отрицательно, но больше –1
производной положительно и больше, чем в других точках
производной положительно, но меньше 1
производной отрицательно и меньше, чем в других точках
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
75
Вариант 2
1. На диаграмме представлено суммарное количества осадков, выпадавших в течение месяца в
некотором городе с января по декабрь. По вертикали указано количество осадков в миллиметрах, а по горизонтали – названия месяцев.
30
25
20
15
10
5
0
январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
Определите по диаграмме, во сколько раз в апреле выпало осадков больше, чем в июне.
2. Н
а рисунках изображены графики функций и касательные к ним в точке x0 . Установите соответствие между графиками функций и значениями их производной в точке x0 .
ГРАФИКИ
А)
Б)
В)
Г)
y
y
y
y
1
x0 0 1
1
1
x0 0 1
1
0 1 x0
x
x
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) 0,66
2) 4,9
3) −3,8
4) −0,5
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
76
А
Б
В
Г
x
0 1 x0
x
§ 6. Теория вероятностей
355. а) В шестом классе учатся 15 мальчиков и 9 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность, что это будет мальчик?
б) В восьмом классе учатся 17 мальчиков и 3 девочки. По жребию они выбирают одного дежурного по классу. Какова вероятность, что это будет девочка?
356. а) На новогоднем празднике в мешке у Деда Мороза содержится 15 кульков с подарками. В
шести из них кроме конфет вложена мягкая игрушка, а в остальные – машинка. Гриша первым
получает из мешка подарок. Найдите вероятность того, что ему достался подарок с машинкой.
б) На новогоднем празднике при проведении викторины каждый из 25 гостей, имеющих разные
имена, вытащил из мешка конверт с заданием. Известно, что в семи из них предлагалось спеть
песню. Найдите вероятность того, что гостье по имени Маша досталось такое задание.
357. а) Из 30 вопросов, содержащихся в списке вопросов к экзамену, студент не выучил 12. На экзамене он случайным образом получает вопрос из списка всех вопросов. Найдите вероятность
того, что ему попадётся выученный вопрос.
б) Для подготовки к экзамену выдано 40 билетов. Студент выучил 35 из них. Найдите вероятность того, что ему попадётся невыученный билет.
358. а) На тарелке лежат одинаковые на вид пирожки: 7 с мясом, 5 с рисом и 18 с луком. Гость наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с луком.
б) На тарелке лежат одинаковые на вид пирожки: 7 с картошкой, 11 с мясом и 12 с малиной.
Гость наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с малиной.
359. а) В фирме такси утром в понедельник свободно 24 машины: 6 белых, 4 жёлтых и 14 зелёных.
На первый заказ выезжает одна случайно выбранная машина. Найдите вероятность, что эта
машина белого цвета.
б) В фирме такси утром в понедельник свободно 30 машин: 7 белых, 15 жёлтых и 8 зелёных.
На первый заказ выезжает одна случайно выбранная машина. Найдите вероятность, что эта
машина жёлтого цвета.
в) В фирме такси утром в понедельник свободно 20 машин: 4 белых, 9 жёлтых и 7 зелёных. На
первый заказ выезжает одна случайно выбранная машина. Найдите вероятность, что эта машина
жёлтого или зелёного цвета.
г) В фирме такси утром в понедельник свободно 36 машин: 13 белых, 14 жёлтых и 9 зелёных.
На первый заказ выезжает одна случайно выбранная машина. Найдите вероятность, что эта
машина белого или жёлтого цвета.
360. а) В соревнованиях по прыжкам в длину участвуют 6 спортсменов из Москвы, 10 спортсменов
из Твери и 4 спортсмена из Тулы. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Тулы.
б) В соревнованиях по прыжкам в длину участвуют 13 спортсменов из Москвы, 2 спортсмена
из Твери и 5 спортсменов из Тулы. Порядок, в котором спортсмены стартуют, определяется
жребием. Найдите вероятность того, что последним будет стартовать спортсмен не из Москвы.
361. а) В магазине одежды продаётся 152 блузки: 32 красных, 36 зелёных, 30 оранжевых, остальные
белые и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине
блузка будет белой или оранжевой.
б) В магазине одежды продаётся 92 юбки: 10 белых, 29 чёрных, 27 жёлтых, остальные бирюзовые и красные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине
юбка будет белой или бирюзовой.
77
362. а) В среднем из 200 наушников, поступивших в продажу, четыре неисправных. Найдите вероятность того, что выбранные наудачу в магазине наушники окажутся исправными.
б) Ателье шьёт пальто. В среднем из 60 пальто 3 пальто имеют брак. Найдите вероятность того,
что случайно выбранное пальто окажется без брака.
в) Из каждых 500 батареек 7 бракованные. Какова вероятность купить исправную батарейку?
г) Из каждых 600 семян подсолнечника в среднем 30 не взойдут. Какова вероятность того, что
случайно выбранное семя прорастёт?
363. а) Музыкальный конкурс длится 3 дня. Всего запланировано 84 выступления: в первый день –
42 выступления, остальные распределены поровну между вторым и третьим днями. На конкурсе
планируется выступление группы «Солнце». Порядок выступлений определяется случайным образом. Какова вероятность того, что выступление группы «Солнце» окажется запланированным
на второй день конкурса?
б) Кинофестиваль длится 4 дня. Всего запланировано к показу 80 кинофильмов: в первый день –
19 кинофильмов, во второй – 17, остальные распределены поровну между третьим и четвёртым
днями. На конкурсе планируется показ кинофильма «Родина». Порядок показов определяется
случайным образом. Какова вероятность того, что показ кинофильма «Родина» окажется запланированным на последний день кинофестиваля?
364. а) В пансионате отдыхающих размещают в трёх корпусах. В первых двух по 120 человек, оставшихся размещают в третьем корпусе. В пансионат приехали 330 отдыхающих. Найдите вероятность того, что случайно выбранный отдыхающий проживает в третьем корпусе. Результат
округлите до сотых.
б) В пансионате отдыхающих размещают в трёх корпусах. В первых двух по 110 человек,
оставшихся размещают в третьем корпусе. В пансионат приехали 270 отдыхающих. Найдите
вероятность того, что случайно выбранный отдыхающий проживает в третьем корпусе. Результат
округлите до сотых.
365. а) У учителя математики в шкафу книг по математике в 9 раз больше, чем книг по истории.
Найдите вероятность того, что случайно выбранная книга из его шкафа будет по истории.
б) У учителя физики в шкафу книг по математике в 4 раза меньше, чем книг по физике. Найдите
вероятность того, что случайно выбранная книга из его шкафа будет по физике.
366. а) Вероятность того, что новый фломастер пишет плохо (или не пишет), равна 0,07. Покупатель
в магазине выбирает один такой фломастер. Найдите вероятность того, что этот фломастер пишет
хорошо.
б) Вероятность того, что новый маркер пишет плохо (или не пишет), равна 0,19. Покупатель в
магазине выбирает один такой маркер. Найдите вероятность того, что этот маркер пишет хорошо.
367. а) Случайным образом выбрано двузначное число. Найдите вероятность того, что оно делится на 5.
б) Случайным образом выбрано трёхзначное число. Найдите вероятность того, что оно делится на 4.
в) Случайным образом выбрано трёхзначное число. Найдите вероятность того, что оно делится на 10.
г) Случайным образом выбрано трёхзначное число. Найдите вероятность того, что оно делится на 48.
368. а) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность
того, что оба раза выпадет орел.
б) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того,
что хотя бы раз выпадет орел.
в) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность
того, что орёл не выпадет ни разу.
78
г) В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того,
что решка выпадет хотя бы один раз.
д) В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность
того, что орел выпадет ровно 2 раза.
369. а) Найдите вероятность того, что при броске игральной кости выпадет четное число.
б) Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число,
меньшее 4.
в) Игральную кость бросают дважды. Найдите вероятность того, что, хотя бы один раз выпало
число большее или равное 4.
г) Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число
большее 3.
д) Игральную кость бросают дважды. Найдите вероятность того, что сумма выпавших очков
равна 7. Результат округлите до сотых.
е) Игральную кость бросают дважды. Найдите вероятность того, что сумма выпавших очков не
меньше 9. Результат округлите до сотых.
370. а) Два игрока играют в кости. Они бросают кость по одному разу. Выигрывает тот, у кого больше очков. Считается ничья, если очков они выбросили поровну. Первый игрок выкинул 4 очка.
Найдите вероятность того, что игрок, бросающий вторым, не проиграет.
б) Два игрока играют в кости. Они бросают кость по одному разу. Выигрывает тот, у кого больше очков. Считается ничья, если очков они выбросили поровну. Первый игрок выкинул 3 очка.
Найдите вероятность того, что игрок, бросающий вторым, выиграет.
371. а) Игральную кость бросают дважды. Известно, что сумма выпавших очков больше
Найдите вероятность события «при одном из бросков выпало 4 очка».
б) Игральную кость бросают дважды. Известно, что сумма выпавших очков больше
Найдите вероятность события «при втором броске выпало 4 очка».
в) Игральную кость бросают дважды. Известно, что сумма выпавших очков больше
Найдите вероятность события «ни при одном из бросков не выпадало меньше 4 очков».
г) Игральную кость бросают дважды. Известно, что сумма выпавших очков больше
Найдите вероятность события «при втором броске выпало 4 очка».
8.
8.
7.
7.
372. а) В чемпионате по стрельбе участвует 61 спортсмен, среди которых 19 спортсменов из Рязани,
в том числе Тамара. Перед началом первого тура чемпионата участников разбивают на игровые
пары случайным образом с помощью жребия. Найдите вероятность того, что в первом туре
Тамара будет соревноваться с каким-либо спортсменом из Рязани.
б) В чемпионате по стрельбе участвует 41 спортсмен, среди которых 13 спортсменов из Нижнего
Новгорода, в том числе Людмила. Перед началом первого тура чемпионата участников разбивают на игровые пары случайным образом с помощью жребия. Найдите вероятность того, что в
первом туре Людмила будет соревноваться с каким-либо спортсменом из Нижнего Новгорода.
373. а) На прилавке случайным образом расставлены тарелки – все разных цветов, среди этих тарелок
есть тарелки синего, красного и белого цветов. Какова вероятность того, что тарелка белого цвета
поставлена после тарелки красного цвета и после тарелки синего цвета? Результат округлите до
сотых.
б) На прилавке случайным образом расставлены тарелки – все разных цветов, среди этих тарелок
есть тарелки синего, зелёного и белого цветов. Какова вероятность того, что тарелка белого цвета поставлена после тарелки синего цвета и перед тарелкой зелёного цвета? Результат округлите до сотых.
79
374. а) В некоторой области вероятность того, что родившийся ребёнок окажется мальчиком, равна
0,547. В 2022 г. в этой области родилось 492 девочки из 1000 новорождённых. Найдите разницу
между частотой рождения девочек в 2022 г. в этой области и вероятностью этого события.
б) В некоторой области вероятность того, что родившийся ребёнок окажется девочкой, равна 0,468.
В 2022 г. в этой области родилось 553 мальчика из 1000 новорождённых. Найдите разницу между
частотой рождения мальчиков в 2022 г. в этой области и вероятностью этого события.
375. а) Люба подбросила монету 1000 раз, из них орёл выпал 446 раз. На сколько частота выпадения
решки в этом случае отличается от вероятности этого события?
б) Лиза подбросила монету 1000 раз, из них решка выпала 513 раз. На сколько частота выпадения
орла в этом случае отличается от вероятности этого события?
376. В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность
того, что орел выпадет ровно 1 раз.
377. а) Вероятность того, что новый холодильник прослужит больше года, равна 0,95. Вероятность
того, что он прослужит два года или больше, 0,81. Найдите вероятность того, что он прослужит
меньше двух лет, но больше года.
б) Вероятность того, что утюг прослужит больше года, равна 0,96. Вероятность того, что он
прослужит два года или больше, 0,73. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
378. а) Команды «Дружба» и «Вперёд» играют два матча между собой в переходном турнире. По
правилам соревнований ничьи в матче не допускаются. Команда «Вперёд» проигрывает команде
«Дружба» с вероятностью 0,3 независимо от результатов предыдущих игр. Определите вероятность того, что «Вперёд» выиграет оба матча.
б) Команды «Дружба» и «Вперёд» играют два матча между собой в переходном турнире. По
правилам соревнований ничьи в матче не допускаются. Команда «Вперёд» выигрывает у команды
«Дружба» с вероятностью 0,4 независимо от результатов предыдущих игр. Определите вероятность того, что «Вперёд» проиграет оба матча.
379. а) На экзамене по истории студенту достаётся один вопрос из всего списка вопросов. Вероятность
того, что это вопрос по теме «Древняя Русь», равна 0,15. Вероятность того, что это окажется
вопрос по теме «Средневековье», равна 0,33. В списке нет вопросов, которые одновременно
относятся к этим двум темам. Найдите вероятность того, что на экзамене студенту достанется
вопрос по одной из этих двух тем.
б) На экзамене по истории студенту достаётся один вопрос из всего списка вопросов. Вероятность
того, что это вопрос по теме «Древняя Русь», равна 0,35. Вероятность того, что это окажется
вопрос по теме «Средневековье», равна 0,18. В списке нет вопросов, которые одновременно
относятся к этим двум темам. Найдите вероятность того, что на экзамене студенту достанется
вопрос по одной из этих двух тем.
380. а) Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что он первый раз попал в мишень, а последние
два раза промахнулся.
б) Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что он первые 3 раза попал в мишени, а последний
раз промахнулся.
80
в) Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле
равна 0,8. Найдите вероятность того, что он первые 3 раза попал в мишени, а последние два
раза промахнулся.
г) Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле
равна 0,8. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний
раз промахнулся. Результат округлите до сотых.
381. а) Вокруг круглого стола в случайном порядке расставляют стулья: 9 металлических и 2 деревянных. Найдите вероятность, что деревянные стулья будут стоять рядом.
б) Семь девочек и два мальчика встают в хоровод в случайном порядке. Найдите вероятность
того, что мальчики не будут стоять в хороводе рядом.
382. а) Вероятность того, что купленный фонарик не работает равна 0,2. Покупатель случайным образом выбирает два фонарика. Какова вероятность, что оба фонарика исправны?
б) Вероятность того, что купленный фонарик не работает равна 0,1. Покупатель случайным образом выбирает два фонарика. Какова вероятность, что хотя бы один из фонариков не работает?
в) Вероятность того, что купленный фонарик не работает равна 0,3. Покупатель случайным образом выбирает два фонарика. Какова вероятность, что хотя бы один из фонариков исправен?
г) Вероятность того, что купленный фонарик работает исправно равна 0,88. Покупатель случайным образом выбирает два фонарика. Какова вероятность, что хотя бы один из фонариков
неисправен?
Проверочная работа № 16
Вариант 1
1.В университетской группе учатся 24 мальчика и 8 девочек. По жребию они выбирают одного
старосту. Какова вероятность, что это будет девочка?
2.
Из 55 вопросов, содержащихся в списке вопросов к экзамену, студент не выучил 11. На экзамене
он случайным образом получает вопрос из списка всех вопросов. Найдите вероятность того,
что ему попадётся выученный вопрос.
3.
В магазине продаётся 4 красных, 11 жёлтых и 10 зеленых тазов. Случайным образом взяли
один таз. Определите вероятность того, что этот таз не жёлтый.
В чемпионате по стрельбе участвуют 31 спортсмен, среди которых 13 спортсменов из Вологды,
4.
в том числе Павел. Перед началом первого тура чемпионата участников разбивают на игровые
пары случайным образом с помощью жребия. Найдите вероятность того, что в первом туре
Павел будет соревноваться с каким-либо спортсменом из Вологды.
5.
Игральную кость бросают дважды. Найдите вероятность того, что, хотя бы один раз выпало
число большее или равное 5. Результат округлите до сотых.
6.
Игральную кость бросают дважды. Известно, что сумма выпавших очков больше 7. Найдите
вероятность события «при первом броске выпало 4 очка».
81
Вариант 2
1.На тарелке лежат фрукты: 5 апельсинов, 11 яблок и 4 персика. Случайным образом взяли один
фрукт. Какова вероятность, что это яблоко?
2.Ателье шьёт пальто. В среднем из 100 пальто 4 пальто имеют брак. Найдите вероятность того,
что случайно выбранное пальто окажется без брака.
3.В магазине продаётся 5 красных, 7 жёлтых и 18 зелёных тазов. Случайным образом взяли один
таз. Определите вероятность того, что этот таз не зелёный.
4.Музыкальный конкурс длится 3 дня. Всего запланировано 56 выступлений: в первый и второй
день по 21 выступлению, а остальные в последний день. На конкурсе планируется выступление
группы «Дружба». Порядок выступлений определяется случайным образом. Какова вероятность
того, что выступление группы «Дружба» окажется запланированным на последний день конкурса?
5.Игральную кость бросают дважды. Найдите вероятность того, что, хотя бы один раз выпало
число меньшее или равное 3. Результат округлите до десятых.
6.Игральную кость бросают дважды. Известно, что сумма выпавших очков меньше 7. Найдите
вероятность события «при первом броске выпало 3 очка».
82
Глава 2. ГЕОМЕТРИЯ
§ 7. Планиметрия
7.1. Прикладные задачи по планиметрии
40 м
383. а) Дачный участок имеет форму прямоугольника, стороны которого
равны 30 м и 40 м. Одна из меньших сторон участка идёт вдоль
озера. Три остальные стороны нужно огородить забором. Найдите
длину этого забора. Ответ дайте в метрах.
б) Участок под строительство отеля имеет форму прямоугольника,
стороны которого равны 300 м и 800 м. Одна из больших сторон
участка идёт вдоль моря. Три остальные стороны нужно огородить
забором. Найдите длину этого забора. Ответ дайте в метрах.
30 м
800 м
300 м
384. а) Кошка бегает по периметру квадратной площадки со стороной 5 м. Сколько раз кошка возвращалась в начальную точку, если она пробежала всего 300 м?
б) Кошка бегает по периметру квадратной площадки со стороной 4 м. Сколько раз кошка возвращалась в начальную точку, если она пробежала всего 192 м?
32 м
385. а) Участок имеет форму прямоугольника со сторонами 25 метров
и 32 метра. Планируется обнести участок забором по периметру и
25 м
разделить его таким же забором на две части. Найдите суммарную
длину забора. Ответ дайте в метрах.
25 м
б) Участок имеет форму прямоугольника со сторонами 15 метров и
25 метров. Планируется обнести участок забором по периметру и
разделить его таким же забором на две части. Найдите суммарную
длину забора. Ответ дайте в метрах.
386. а) Участок имеет прямоугольную форму. Стороны участка равны
25 м и 75 м. Найдите длину забора, которым нужно огородить участок, предусмотрев проезд шириной 3 м. Ответ дайте в метрах.
б) Участок имеет прямоугольную форму. Стороны участка равны
20 м и 30 м. Найдите длину забора, которым нужно огородить
участок, предусмотрев проезд шириной 3 м. Ответ дайте в метрах.
387. а) На рисунке изображена схема коммерческого помещения. Помещение состоит из рабочей зоны, склада,
офиса и кладовой. Размеры отмечены на чертеже (в
метрах). Пользуясь рисунком найдите площадь кладовой. Ответ дайте в квадратных метрах.
15 м
75 м
3м
25 м
30 м
3м
20 м
7м
10 м
Рабочая
зона
Склад
Кл.
Офис
7м
3м
13 м
83
б) На рисунке изображена схема коммерческого помещения. Помещение состоит из рабочей зоны, склада,
комнаты отдыха, кладовой и коридора. Размеры отмечены на чертеже (в метрах). Пользуясь рисунком
найдите площадь рабочей зоны. Ответ дайте в квадратных метрах.
3м
4м
2м
Комната
отдыха
5м
Рабочая
зона
Склад
Кл.
Коридор
2м
10 м
388. а) Дачный участок имеет форму прямоугольника со сторонами 30 м и
35 м. Дом, расположенный на участке, имеет форму прямоугольника,
стороны которого равны 10 м и 5 м. Найдите площадь свободной
части участка (без дома). Ответ дайте в квадратных метрах.
30 м
5м
35 м
10 м
40 м
б) Дачный участок имеет форму прямоугольника со сторонами 30 м и
40 м. Дом, расположенный на участке, имеет форму квадрата, стороны
которого равны 8 м. Найдите площадь свободной части участка (без
дома). Ответ дайте в квадратных метрах.
8м
30 м
8м
389. а) На плане квартиры указано, что комната имеет площадь 12,7 квадратных метров. Точные
измерения показали, что ширина комнаты 2,7 м, а длина 4,7 м. На сколько квадратных метров
отличаются площади комнаты на плане и в реальности? Ответ дайте в квадратных мерах.
б) На плане квартиры указано, что комната имеет площадь 18,8 квадратных метров. Точные
измерения показали, что ширина комнаты 3,4 м, а длина 5,3 м. На сколько квадратных метров
отличаются площади комнаты на плане и в реальности? Ответ дайте в квадратных мерах.
390. а) Пол комнаты имеет форму квадрата со стороной 8 м.
Паркет состоит из прямоугольных дощечек со сторонами
таких дощечек для покрытия пола паркетом?
б) Пол комнаты имеет форму квадрата со стороной 6 м.
Паркет состоит из прямоугольных дощечек со сторонами
таких дощечек для покрытия пола паркетом?
Его необходимо покрыть паркетом.
5 см и 20 см. Сколько потребуется
Его необходимо покрыть паркетом.
4 см и 15 см. Сколько потребуется
?
391. а) На расстоянии 12 метров от дома вкопали столб высотой
7 метров. От вершины столба к стене дома протянули
кабель и закрепили его на высоте 2 метра от земли. Найдите
длину кабеля в метрах.
7м
2м
12 м
б) На расстоянии 12 метров от дома вкопали столб. От
вершины столба к стене дома протянули кабель длиной
15 метров и закрепили его на высоте 3 метра от земли.
Найдите высоту столба в метрах
15 м
?
3м
84
12 м
17 м
?м
392. а) Лестницу длиной 17 м приставили к чердаку дома. Расстояние от стены
дома до нижнего конца лестницы равно 8 м.. На какой высоте расположен
чердак? Ответ дайте в метрах.
8м
б) Лестницу длиной 25 м приставили к чердаку дома. Расстояние от стены
дома до нижнего конца лестницы равно 7 м. На какой высоте расположен
?м
чердак? Ответ дайте в метрах.
25 м
7м
393. а) Высота h деревянной горки, которую посередине подпирает
столб, равна 3 м. Найдите высоту l этого столба в метрах..
б) Деревянную горку посередине подпирает столб, высота которого
равна 1,25 м. Найдите высоту h этой горки в метрах.
h
l
394. а) Перила лестницы крепятся на три столба, один из которых
расположен посередине перил. Наименьший столб имеет высоту
1,5 м, наибольший – 2 м. Найдите высоту среднего столба в
метрах.
б) Перила лестницы крепятся на три столба, один из которых
расположен посередине перил. Наименьший столб имеет высоту
1,5 м, наибольший – 2 м. Найдите высоту среднего столба
в метрах.
395. а) Ребёнок стоит на расстоянии 4 м от фонарного столба, высотой
6 м. Тень ребёнка равна 1 м. Найдите рост ребёнка. Ответ дайте в
метрах.
6м
?
1м 4м
б) Мужчина ростом 1,8 м стоит возле фонарного столба высотой
9 м. Длина отбрасываемой мужчиной тени 1 м. На каком расстоянии
от столба стоит мужчина? Ответ дайте в метрах.
9м
1,8 м
1м
?
85
11
12
1
10
2
9
3
8
396. а) Какой угол образуют минутная и часовая стрелки часов в 19:00? Ответ
дайте в градусах.
б) Какой угол образуют минутная и часовая стрелки часов в 11:00? Ответ дайте в градусах.
4
7
6
5
397. а) В колесе углы между соседними спицами равны. Сколько спиц в колесе,
если угол между соседними спицами равен 30°?
б) В колесе 45 спиц. Углы между соседними спицами равны. Найдите угол между двумя соседними спицами. Ответ дайте в градусах.
Проверочная работа № 17
Вариант 1
1. Д
ачный участок имеет форму прямоугольника, стороны которого равны 26 м и 57 м. Одна из меньших сторон участка идёт
вдоль озера. Три остальные стороны нужно огородить забором.
Найдите длину этого забора. Ответ дайте в метрах.
2. На расстоянии 15 метров от дома вкопали столб высотой 12
метров. От вершины столба к стене дома протянули кабель
и закрепили его на высоте 4 метра от земли. Найдите длину
кабеля в метрах.
?
12 м
4м
15 м
3. Какой угол образуют минутная и часовая стрелки часов в 14:00? Ответ дайте в градусах.
48 см
иагональ экрана равна 60 см, а длина 48 см. Найдите площадь
4. Д
экрана. Ответ дайте в квадратных сантиметрах.
60
см
ол комнаты имеет форму квадрата со стороной 15 м. Его необходимо покрыть паркетом.
5. П
Паркет состоит из прямоугольных дощечек со сторонами 6 см и 25 см. Сколько потребуется
таких дощечек для покрытия пола паркетом?
86
Вариант 2
часток имеет прямоугольную форму. Стороны участка равны 28 м и 84 м. Найдите длину
1. У
забора, которым нужно огородить участок, предусмотрев проезд шириной 4 м. Ответ дайте в
метрах.
13 м
2. Н
а расстоянии 12 метров от дома вкопали столб. От вершины столба к
стене дома протянули кабель длиной 13 метров и закрепили его на высоте 4 метра от земли. Найдите высоту столба в метрах.
?
4м
колесе углы между соседними спицами равны. Сколько спиц в колесе,
3. В
если угол между соседними спицами равен 15°?
12 м
32 см
иагональ экрана равна 40 см, а длина 32 см. Найдите площадь экрана.
4. Д
Ответ дайте в квадратных сантиметрах.
40
см
5. Д
ачный участок имеет форму прямоугольника со сторонами 20 м и 40 м. Дом, расположенный на участке, имеет форму прямоугольника, стороны которого равны 10 м и 12 м. Найдите площадь свободной части участка (без дома). Ответ дайте в квадратных метрах.
398. На плане местности одна клетка имеет размеры 1 м на 1 м. Найдите площадь участков, выделенных на плане. Ответ дайте в квадратных метрах.
А)
а)
Б)
б)
В)
в)
Г)
г)
399. На плане местности одна клетка имеет размеры 1 м на 1 м. Найдите площадь участков, выделенных на плане. Ответ дайте в квадратных метрах.
А) а)
Б)
б)
В)в)
Г)
г)
87
400. На плане местности одна клетка имеет размеры 1 м на 1 м. Найдите площадь участков, выделенных на плане. Ответ дайте в квадратных метрах.
А)
а)
Б)
б)
В)
в)
Г)
г)
401. На плане местности одна клетка имеет размеры 1 м на 1 м. Найдите площадь участков, выделенных на плане. Ответ дайте в квадратных метрах.
А)
а)
Б)
б)
В)
в)
Г)
г)
402. На плане местности одна клетка имеет размеры 1 м на 1 м. Найдите площадь участков, выделенных на плане. Ответ дайте в квадратных метрах.
а)
б)
в)
г)
403. На плане местности одна клетка имеет размеры 1 м на 1 м. Найдите площадь участков, выделенных на плане. Ответ дайте в квадратных метрах.
А)
а)
88
Б)
б)
В)
в)
Г)
г)
404. На фрагменте географической карты схематично изображены границы парка «Дружба» (площадь
одной клетки равна одному гектару). Оцените приближённо площадь парка. Ответ дайте в гектарах с округлением до целого значения.
405. На фрагменте географической карты схематично изображены границы лесного массива (площадь
одной клетки равна одному гектару). Оцените приближённо площадь лесного массива. Ответ
дайте в гектарах с округлением до целого значения.
406. На фрагменте географической карты схематично изображены границы городского района Битово
(площадь одной клетки равна одному гектару). Оцените приближённо площадь района. Ответ
дайте в гектарах с округлением до целого значения.
407. На фрагменте географической карты схематично изображено озеро Солнечное (площадь одной
клетки равна одному гектару). Оцените приближённо площадь озера. Ответ дайте в гектарах с
округлением до целого значения.
89
Проверочная работа № 18
Вариант 1
1. На плане местности одна клетка имеет размеры 1 м на 1 м. Найдите площадь участков, выделенных на плане. Ответ дайте в квадратных метрах.
А)а)
Б)
В)
б)
в)
г) Г)
2. На фрагменте географической карты схематично изображены границы парка «Дружба» (площадь одной клетки равна одному гектару). Оцените приближённо площадь парка. Ответ дайте в
гектарах с округлением до целого значения.
Вариант 2
1. На плане местности одна клетка имеет размеры 1 м на 1 м. Найдите площадь участков, выделенных на плане. Ответ дайте в квадратных метрах.
г)
а)
А)
Б) б)
В)в)
Г)
2. На фрагменте географической карты схематично изображены границы парка «Дружба» (площадь одной клетки равна одному гектару). Оцените приближённо площадь парка. Ответ дайте в
гектарах с округлением до целого значения.
90
7.2. Углы и длины
408. а) Три прямые пересекаются в одной точке. На рисунке одинаковыми дугами отмечены равные углы. Найдите угол a. Ответ дайте в градусах.
б) Три прямые пересекаются в одной точке. На рисунке одинаковыми
дугами отмечены равные углы. Найдите угол a. Ответ дайте в градусах.
α
44º
M
409. а) На прямой CD отмечена точка Р. Луч PK – биссектриса угла MРD.
50° . Найдите величину угла MPC . Ответ дайте
Известно, что ∠ KPM =
в градусах.
96º
α
K
C
б) На прямой AB отмечена точка S. Луч SM – биссектриса угла ASM.
P
D
S
B
N
94° . Найдите величину угла NSM . Ответ дайте в M
Известно, что ∠ NSB =
градусах.
A
410. а) Прямые a и b параллельны. Найдите ∠ 3 , если ∠1 = 75° , а ∠ 2 = 85° .
Ответ дайте в градусах.
a
б) Прямые a и b параллельны. Найдите ∠ 2 , если ∠1 = 55° , а ∠ 3 = 62° .
Ответ дайте в градусах.
b
1
2
3
411. Используя рисунок, найдите угол a. Ответ дайте в градусах.
а)
А)
б)
Б)
55º
112º
62º
α
69º
α
412. а) В треугольнике ABC известно, что AB=BC. Найдите угол BCA, если ∠ ABC =°
86 . Ответ дайте
в градусах.
б) В треугольнике ABC известно, что AB=BC. Найдите угол ABC, если ∠ BAC =°
15 . Ответ дайте
в градусах.
C
413. а) В треугольнике ABC стороны AC и BC равны. Внешний угол
при вершине В равен 144° . Найдите угол С. Ответ дайте в градусах.
б) В треугольнике ABC стороны AC и BC равны. Внешний угол A
при вершине В равен 158° . Найдите угол С. Ответ дайте в градусах.
414. а) В треугольнике ABC известно, что ∠ BAD =
47° , ∠ B = 36° , AD –
биссектриса. Найдите угол С. Ответ дайте в градусах.
б) В треугольнике ABC известно, что ∠ DAC =°
33 , ∠ C = 29° , AD –
биссектриса. Найдите угол B. Ответ дайте в градусах.
A
B
B
D
C
91
415. а) В треугольнике ABC проведена биссектриса AD, угол ADC равен 67°, а угол ABC равен 40°.
Найдите угол ACB. Ответ дайте в градусах.
б) В треугольнике ABC проведена биссектриса AD, угол ADB равен 117°, а угол ACB равен
67°. Найдите угол ABC . Ответ дайте в градусах.
416. а) В остроугольном треугольнике ABC проведена высота BH. Найдите
B
35 . Ответ дайте в градусах.
угол ABH, если ∠ BAC =°
б) В остроугольном треугольнике ABC проведена высота BH. Найдите
72° и ∠ ABC =°
53 . Ответ дайте в градусах.
угол ABH, если ∠ BCA =
A
H
C
417. а) Углы треугольника относятся как 2:3:4. Найдите больший угол треугольника. Ответ дайте в
градусах.
б) Углы треугольника относятся как 2:7:9. Найдите меньший угол треугольника. Ответ дайте в
градусах.
418. а) Диагональ RP параллелограмма KPNR в два раза больше его стороны KR. Найдите угол между диагоналями параллелограмма, если
P
K
∠ KRO =
124° . Ответ дайте в градусах.
O
R
б) В параллелограмме ABCD диагональ АС в два раза больше стороны B
AB и ∠ ACD =
5° . Найдите угол между диагоналями параллелограмма.
Ответ дайте в градусах.
N
C
A
D
419. а) Диагональ прямоугольника образует с одной из его сторон угол 38°.
Найдите угол между диагоналями этого прямоугольника.
б) Диагональ прямоугольника образует с одной из его сторон угол 18°. Найдите тупой угол
между диагоналями этого прямоугольника.
420. а) Диагональ AC параллелограмма ABCD образует с его сторонами углы 35° и 53°. Найдите
больший угол параллелограмма.
б) Диагональ AC параллелограмма ABCD образует с его сторонами углы 49° и 73°. Найдите
меньший угол параллелограмма.
421. а) Острый угол ромба равен 54°. Найдите угол между его меньшей диагональю и стороной.
б) В ромбе угол между меньшей диагональю и стороной равен 80°. Найдите меньший угол ромба.
422. а) В равнобедренной трапеции ABCD с основаниями BC и AD угол A равен 66°. Найдите ∠C.
б) Угол D равнобедренной трапеции ABCD с основаниями BC и AD равен 112°. Найдите ∠B.
в) Сумма двух углов равнобедренной трапеции равна 112°. Найдите больший угол трапеции.
г) Разность двух углов равнобедренной трапеции равна 84°. Найдите меньший угол трапеции.
д) Два угла равнобедренной трапеции относятся как 4:5. Найдите меньший угол трапеции.
е) Один из углов прямоугольной трапеции равен 35°. Найдите больший угол трапеции.
92
423. а) Диагональ AC равнобедренной трапеции ABCD с основаниями AD и BC образует с основанием
BC и боковой стороной AB углы 36° и 42° соответственно. Найдите угол ADC.
б) Диагональ AC равнобедренной трапеции ABCD с основаниями AD и BC образует с основанием
AD и боковой стороной CD углы 44° и 102° соответственно. Найдите угол ABC.
в) Диагональ AC равнобедренной трапеции ABCD с основаниями AD и BC образует с основанием
BC и боковой стороной CD углы 37° и 113° соответственно. Найдите меньший угол трапеции.
г) Диагональ AC равнобедренной трапеции ABCD с основаниями AD и BC образует с основанием
AD и боковой стороной AB углы 28° и 46° соответственно. Найдите больший угол трапеции.
C
424. а) В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD,
∠ B = 60° , ∠ D = 150° . Найдите угол А. Ответ дайте в градусах.
б) В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD,
B
D
∠ B = 70° , ∠ D = 170° . Найдите угол А. Ответ дайте в градусах.
A
F
E
425. а) На рисунке изображён правильный восьмиугольник. Найдите его угол.
G
Ответ дайте в градусах.
D
H
C
A
B
E
D
F
б) На рисунке изображён правильный десятиугольник. Найдите его угол.
C
Ответ дайте в градусах.
G
B
H
A
426. В треугольнике ABC угол B – прямой.
а) найдите cos A , если sin A =
3
;
2
б) найдите sin A , если cos A = 0,6 ;
в) найдите tg A , если sin A =
2
;
2
г) найдите tg A , если sin A = 0,6 .
I
427. а) В треугольнике ABC угол B – прямой. Найдите AC, если cos A = 0,6 , BA = 12 .
б) В треугольнике ABC угол B – прямой. Найдите AC, если sin C = 0,12 , BA = 3 .
428. а) В треугольнике ABC угол B – прямой. Найдите AC, если cos A =
б) В треугольнике ABC угол B – прямой. Найдите AC, если sin C =
5
, BC = 24 .
13
5
, BC = 24 .
7
93
5 11
, BC = 5 .
11
429. а) В треугольнике ABC угол B – прямой. Найдите AC, если tgA =
7
, BC = 6 .
3
б) В треугольнике ABC угол B – прямой. Найдите AC, если tgC =
19
, AC = 10 .
9
430. а) В треугольнике ABC угол B – прямой. Найдите AB, если tgA =
б) В треугольнике ABC угол B – прямой. Найдите BC, если tgC =
11
, ÀC = 12
5
= BC
= 25 , AC = 48 . Найдите
431. а) В треугольнике ABC известно, что AB
B
sin A .
= BC
= 20 , AC = 32 . Найдите
б) В треугольнике ABC известно, что AB
sin A .
432. а) В треугольнике ABC угол B равен 120°, медиана BC одновременно является высотой треугольника. Найдите длину стороны
АВ.
б) В треугольнике ABC угол B равен 120°, высота BM одновременно является медианой треугольника. Найдите длину BM,
если BM = 64.
A
C
B
A
C
М
433. а) В равнобедренном треугольнике ABC, AB = BC , высота BH = 1 , tgA = 1 . Найдите АС.
б) В равнобедренном треугольнике ABC, AB = BC , основание AC = 1 , tgC = 3 . Найдите высоту
BH.
C
434. а) В прямоугольном треугольнике ABC, угол С – прямой, СН – высота, AC = 4 , cos A = 0,8 . Найдите длину отрезка АН.
б) В прямоугольном треугольнике ABC, угол С – прямой, СН – высота, AC = 12 , sin A = 0,3 . Найдите высоты CН.
A
435. а) В прямоугольном треугольнике ABC внешний угол при вершине А
равен 150°. Катет BC = 6. Найдите гипотенузу треугольника ABC.
б) В прямоугольном треугольнике ABC внешний угол при вершине
А равен 150°. Гипотенуза треугольника равна 18. Найдите катет ВС.
436. а) В равнобедренном треугольнике АВС внешний угол при основании АС равен 150°, а медиана BM = 10. Найдите боковую сторону
треугольника
б) В равнобедренном треугольнике АВС внешний угол при основании
A
АС равен 150° а боковая сторона AB = 70. Найдите высоту ВМ.
94
H
B
B
A
C
B
M
C
437. а) В треугольнике АВС внешние углы при вершинах А и С равны
150°, AB = 30, найдите высоту ВК.
б) В треугольнике АВС внешние углы при вершинах А и С равны
150°, биссектриса BK = 5, AC = 2 75 . Найдите ВС.
B
A
K
C
B
438. а) В ромбе АВСD большая диагональ равна 20 3 , а меньшая диагональ
равна 20. Найдите угол DCA. Ответ дайте в градусах.
б) В ромбе АВСD большая диагональ равна 10 2 , а сторона равна 10. A
Найдите угол DCA. Ответ дайте в градусах.
C
D
439. а) В равнобедренной трапеции одно из оснований равно 13, а другое
равно 9. Высота трапеции равна 5. Найдите значение тангенса острого угла трапеции.
б) В равнобедренной трапеции боковая сторона равна 10. Высота трапеции равна 5. Найдите
значение синуса острого угла трапеции.
440. а) Тангенс острого угла прямоугольной трапеции равен 0,8. Найдите её большее основание, если
меньшее основание равно высоте и равно 16.
9
б) Тангенс острого угла прямоугольной трапеции равен . Найдите её большее основание, если
7
меньшее основание равно высоте и равно 36.
441. а) В треугольнике ABC угол B равен 30°, угол C равен 60°, AB = 6 3 . Найдите AC.
б) В треугольнике ABC угол A равен 30°, угол C равен 45°, AB = 7 2 . Найдите BC.
442. а) В треугольнике ABC стороны AC, CB и AB равны соответственно 6, 7 и 8. Найдите cos C.
б) В треугольнике ABC стороны AC, CB и AB равны соответственно 4, 5 и 6. Найдите cos A.
443. а) Точки K и P являются серединами сторон AB и CB треугольника ABC. Стороны AC, AB и CB
соответственно равны 7, 12 и 16. Найдите KP.
б) Точки K и P являются серединами сторон AC и CB треугольника ABC. Стороны AC, AB и CB
соответственно равны 8, 14 и 21. Найдите KP.
444. а) Прямая параллельная стороне AB треугольника ABC пересекает его стороны AC и BC в точках
K и M соответственно, CB = 21, AB = 36, KM = 12. Найдите CM.
б) Прямая параллельная стороне AC треугольника ABC пересекает его стороны AB и BC в точках
K и M соответственно, AB = 20, AC = 32, KM = 8. Найдите KB.
445. а) Прямая параллельная стороне AB треугольника ABC пересекает его стороны AC и BC в точках
K и M соответственно, CB = 15, AB = 20, KM = 4. Найдите MB.
б) Прямая параллельная стороне AC треугольника ABC пересекает его стороны AB и BC в точках
K и M соответственно, AB = 18, AC = 27, KM = 9. Найдите AK.
446. а) В треугольнике ABC проведена медиана BM и высота BK. Найдите
KC, если AB = BM и AC = 68.
б) В треугольнике ABC проведена медиана BM и высота BK. Найдите
AC, если AB = BM и KC = 42.
B
A
K
M
C
447. а) Найдите гипотенузу прямоугольного треугольника, если его катеты
равны 6 и 8.
б) Найдите гипотенузу прямоугольного треугольника, если его катеты равны 7 и 24.
95
448. а) Найдите медиану прямоугольного треугольника, проведённую к гипотенузе, если его катеты
равны 9 и 12.
б) Найдите медиану прямоугольного треугольника, проведённую к гипотенузе, если его катеты
равны 3 и 4.
449. а) В треугольнике АВС угол В – прямой, точка К – середина АС. Найдите длину медианы ВК,
если AB = 8, AC = 19.
б) В треугольнике АВС угол В – прямой, точка К – середина АС. Найдите длину медианы ВК,
если AC = 20, CB = 8.
450. а) Найдите
равны 18 и
б) Найдите
равны 14 и
высоту прямоугольного треугольника, проведённую к гипотенузе, если его катеты
24.
высоту прямоугольного треугольника, проведённую к гипотенузе, если его катеты
48.
451. а) Найдите высоту прямоугольного треугольника, проведённую к гипотенузе, если отрезки, на
которые она делит гипотенузу, равны 2 и 4,5.
б) Найдите высоту прямоугольного треугольника, проведённую к гипотенузе, если отрезки, на
которые она делит гипотенузу, равны 4 и 9.
452. а) В треугольнике ABC проведена медиана BK. Известно, что AB = BC. Найдите AC, если
AB = 50, а BK = 14.
б) В треугольнике ABC проведена биссектриса BK. Известно, что AB = BC. Найдите BK, если
AB = 30, а AC = 36.
453. а) Найдите сторону равностороннего треугольника, если его биссектриса равна 5 3 .
б) Найдите сторону равностороннего треугольника, если его медиана равна 8 3 .
454. а) Найдите биссектрису равностороннего треугольника, если его сторона равна 12 3 .
б) Найдите медиану равностороннего треугольника, если его сторона равна 13 3 .
455. а) Найдите сторону квадрата, если его диагональ равна 3 2 .
б) Найдите сторону квадрата, если его диагональ равна
50 .
456. а) Найдите диагональ квадрата, если его сторона равна 3 2 .
б) Найдите диагональ квадрата, если его сторона равна
50 .
457. а) Диагонали AC и BD прямоугольника ABCD пересекаются в точке O. Найдите длину диагонали
BD, если CO = 12 и AD = 20.
б) Диагонали AC и BD прямоугольника ABCD пересекаются в точке O. Найдите длину диагонали
BD, если AO = 5 и AB = 6.
458. а) В параллелограмме KMPD биссектриса DO делит его сторону MP
M
на отрезки MO = 21 и OP = 13. Найдите сторону KM.
б) Найдите периметр параллелограмма KMPD, если биссектриса DO
делит его сторону MP на отрезки MO = 18 и OP = 12.
459. а) Высота равнобедренной трапеции ABCD, проведённая из вершины C, делит основание AD на отрезки длиной 14 и 5. Найдите длину основания BC.
б) Основания равнобедренной трапеции равны 20 и 32, боковая сторона
10. Найдите высоту трапеции.
96
O
K
P
D
460. а) Основания равнобедренной трапеции равны 4 и 14, боковая сторона
равна 13. Найдите длину диагонали трапеции.
б) Основания равнобедренной трапеции равны 50 и 104, боковая сторона
равна 45. Найдите длину диагонали трапеции.
B
С
A
D
461. а) Диагонали AC и BD трапеции ABCD с основаниями AD и BC пересекаются в точке O,
AD = 18, BC = 6, AC = 20. Найдите AO.
б) Диагонали AC и BD трапеции ABCD с основаниями AD и BC пересекаются в точке O,
AD = 24, BC = 4, BD = 21. Найдите BO.
Проверочная работа № 19
Вариант 1
1. На прямой CD отмечена точка Р. Луч РК – биссектриса угла MPD.
56° . Найдите величину угла MPC.
Известно, что ∠ KPM =
M
K
C
P
D
2. В треугольнике ABC известно, что AB = BC. Найдите угол BCA, если внешний угол при вершине
B равен 134°.
3. Сумма двух углов параллелограмма равна 136°. Найдите больший угол параллелограмма.
4. В треугольнике ABC угол B равен 135°, угол C равен 30°, AB = 10 2 . Найдите AC.
5. В треугольнике KMN точки A и C являются серединами сторон KM и MN соответственно. Отрезки KC и NA пересекаются в точке O, KC = 24, NA = 36. Найдите KO.
6. Высота ромба равна 18, а один из углов 150°. Найдите периметр ромба.
7. Основания равнобедренной трапеции равны 8 и 32, боковая сторона 13. Найдите высоту трапеции.
8. В прямоугольном треугольнике ABC, угол С – прямой, высота CН = 8, tg B = 0,8 . Найдите длину
отрезка ВН.
Вариант 2
1. На прямой АВ отмечена точка S. Луч SM – биссектриса угла АSN. M
Известно, что ∠ MSB =
108° . Найдите величину угла NSB.
A
N
S
B
2. Углы треугольника относятся как 1:2:6. Найдите больший угол треугольника.
3. Диагональ прямоугольника образует с одной из его сторон угол 22°. Найдите угол между диагоналями этого прямоугольника.
4. В треугольнике ABC стороны AC, CB и AB равны соответственно 8, 10 и 14. Найдите cos C.
5. Точки K и P являются серединами сторон AB и CB треугольника ABC. Стороны AC, AB и CB
соответственно равны 12, 14 и 23. Найдите KP.
6. Найдите периметр ромба, если один из его углов равен 120°, а меньшая диагональ равна 14.
7. Диагонали AC и BD трапеции ABCD с основаниями AD и BC пересекаются в точке O,
AD = 24, BC = 8, AC = 16. Найдите AO.
8. В прямоугольном треугольнике ABC, угол С – прямой, высота CН = 21, tgA = 1, 4 . Найдите длину
отрезка AН.
97
7.3. Площади
462. а) Найдите площадь треугольника, если сторона и высота, проведённая к этой стороне, соответственно равны 8 и 15.
б) Найдите площадь треугольника, если сторона и высота, проведённая к этой стороне, соответственно равны 4 и 17.
463. а) Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 8 и 17.
б) Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 5 и 13.
464. а) Найдите площадь
сторона и основание
б) Найдите площадь
сторона и основание
B
равнобедренного треугольника, если его боковая
соответственно равны 10 и 16.
равнобедренного треугольника, если его боковая
A
соответственно равны 25 и 48.
C
465. а) Найдите площадь треугольника, если одна из его сторон равна 10, другая равна 6 3 , а угол
между ними равен 60°.
б) Найдите площадь треугольника, если одна из его сторон равна 6, другая равна 10 2 , а угол
между ними равен 45°.
466. а) В треугольнике ABC AB = 13, BC = 14, AC = 15. Найдите его площадь.
б) В треугольнике ABC AB = 13, BC = 20, AC = 21. Найдите его площадь.
467. а) В треугольнике ABC отрезок MN является средней линией, параллельной
стороне AC. Площадь треугольника ABC равна 124. Найдите площадь треугольника MBN.
б) В треугольнике ABC отрезок MN является средней линией, параллельной
стороне AC. Площадь треугольника MBN равна 23. Найдите площадь треугольника ABC.
B
M
A
N
C
468. а) В треугольнике ABC отрезок MN является средней линией, параллельной стороне AC. Площадь
треугольника ABC равна 76. Найдите площадь четырёхугольника AMNC.
б) В треугольнике ABC отрезок MN является средней линией, параллельной стороне AC. Площадь
четырёхугольника AMNC равна 84. Найдите площадь треугольника ABC.
B
15
469. а) В прямоугольном треугольнике ABC угол С прямой, cos B = , AB = 34.
17
Найдите площадь треугольника ABC.
60
б) В треугольнике ABC угол С прямой, cos B =
, AB = 122. Найдите площадь
61
A
треугольника ABC.
98
C
470. а) Сторона равностороннего треугольника равна 4. Найдите его площадь, делённую на
б) Высота равностороннего треугольника равна 6. Найдите его площадь, делённую на
3.
3.
471. а) В треугольнике со сторонами 8 и 4 проведены высоты к этим сторонам. Высота, проведённая
к первой стороне, равна 6. Найдите высоту, проведённую ко второй стороне.
б) В треугольнике со сторонами 8 и 12 проведены высоты к этим сторонам. Найдите большую
из этих высот, если меньшая из них равна 4.
472. а) Две стороны параллелограмма равны 8 и 10, а меньшая высота
равна 4. Найдите большую высоту параллелограмма.
б) Две стороны параллелограмма равны 12 и 15, а большая высота
равна 10. Найдите меньшую высоту параллелограмма.
473. а) В прямоугольнике одна сторона равна 84, а диагональ равна 91.
Найдите его площадь.
б) В прямоугольнике одна сторона равна 52, а диагональ равна 65.
Найдите его площадь.
474. а) Высота BH параллелограмма ABCD делит его сторону AD
на отрезки AH = 2 и HD = 64. Диагональ параллелограмма BD
равна 80. Найдите площадь параллелограмма.
б) Высота BH параллелограмма ABCD делит его сторону AD
на отрезки AH = 6 и HD = 75. Диагональ параллелограмма BD
равна 85. Найдите площадь параллелограмма.
475. а) Найдите площадь параллелограмма, если его стороны равны 3 и 6, а острый угол равен 30°.
б) Найдите площадь параллелограмма, если его стороны равны 4 и 2 2 а тупой угол равен 135°.
476. а) Найдите площадь ромба, если его диагонали равны 6 и 14.
б) Найдите площадь ромба, если одна из диагоналей равна 16, а сторона равна 10.
477. а) Найдите площадь ромба, если его высота равна 4, а острый угол
равен 30°.
б) Найдите площадь ромба, если его сторона равна 4, а острый угол
равен 30°.
478. а) Найдите площадь равнобедренной трапеции, если её основания равны 5 и
15, а боковые стороны равны 13.
б) Найдите площадь равнобедренной трапеции, если её основания равны
2 и 14, а боковые стороны равны 10.
479. а) Найдите площадь равнобедренной трапеции, если её основания равны 7
и 11, а один из углов между боковой стороной и основанием равен 45°.
б) Найдите площадь равнобедренной трапеции, если её основания равны 6 и 20, а один из углов
между боковой стороной и основанием равен 135°.
99
480. а) Основания трапеции равны 17 и 53, одна из боковых сторон равна 14, а косинус угла между
ней и одним из оснований равен
4 3
. Найдите площадь трапеции.
7
б) Основания трапеции равны 17 и 13, одна из боковых сторон равна 6, а тангенс угла между
ней и одним из оснований равен
2
. Найдите площадь трапеции.
4
481. а) В трапеции ABCD с основаниями AD
равна 69. Найдите площадь треугольника
б) В трапеции ABCD с основаниями AD
равна 22. Найдите площадь треугольника
и BC известно, что AD = 4, BC = 2, а её площадь
ABC.
и BC известно, что AD = 6, BC = 5, а её площадь
AСВ.
482. а) Найдите площадь кругового сектора, если его центральный угол равен 120°, а площадь круга
равна 93.
б) Найдите площадь кругового сектора, если его центральный угол равен 72°, а площадь круга равна 200.
Проверочная работа № 20
Вариант 1
1. Найдите площадь равнобедренного треугольника, если его боковая сторона равна 17, а основание равно 30.
2. В треугольнике ABC отрезок MN является средней линией параллельной стороне AC. Площадь
треугольника ABC равна 44. Найдите площадь четырёхугольника AMNC.
3. Найдите площадь квадрата, если его диагональ равна 10.
4. Найдите площадь параллелограмма, если его две стороны равны 3 и 7, а угол между ними 150°.
5. Найдите площадь ромба, если его периметр равен 20, а высота равна 2.
6. Площадь прямоугольника ABCD равна 320, tgBAC = 3,2 . Найдите длину BC.
7. Найдите площадь равнобедренной трапеции, основания которой равны 14 и 32, а боковая сторона равна 15.
8. Площадь кругового сектора, центральный угол которого равен 60°, равна 12. Найдите площадь
всего круга.
Вариант 2
1. Найдите площадь треугольника, если одна из его сторон равна 5, другая сторона равна 12, а
угол между ними равен 30°.
2. На стороне AC треугольника ABC отмечена точка P. Площадь треугольника ABC равна 38. Найдите площадь треугольника BCP, если=
AP 7,=
PC 12 .
3. Найдите площадь прямоугольника, если его диагональ равна 13, а одна из сторон равна 5.
4. Найдите большую высоту параллелограмма, если две его стороны равны 14 и 35, а меньшая
высота равна 2.
5. Найдите площадь ромба, если его периметр равен 36, а один из углов 150°.
6. Площадь прямоугольника ABCD равна 600, tgACD = 1,5 . Найдите длину CD.
7. Найдите площадь равнобедренной трапеции, основания которой равны 28 и 60, а боковая сторона равна 20.
8. Площадь кругового сектора, центральный угол которого равен 90°, равна 23. Найдите площадь
всего круга.
100
7.4. Окружность
483. а) В окружности с центром в точке O проведены диаметры AD и BC, угол
OAB равен 47°. Найдите величину угла OCD. Ответ дайте в градусах.
б) В окружности с центром в точке O проведены диаметры AD и BC, угол
OCD равен 78°. Найдите величину угла OAB. Ответ дайте в градусах.
484. а) В окружности с центром в точке O проведены диаметры AD и BC, угол
ABO равен 66°. Найдите величину угла CDO. Ответ дайте в градусах.
б) В окружности с центром в точке O проведены диаметры AD и BC, угол
CDO равен 31°. Найдите величину угла ABO. Ответ дайте в градусах.
485. Найдите величину угла ABC в каждом пункте, если известны градусные меры дуг AB и BC.
а)
а)
120º
B
б)
в)
в)
г)
г)
C
B
70º
C
A
б)
C
A
76º
220º
B
134º
88º
A
86º
A
C
B
168º
B
486. а) Найдите градусную меру центрального угла AOB, если известно, что
BC – диаметр, а угол ABC равен 20°. Ответ дайте в градусах.
A
O
C
A
B
б) Найдите градусную меру угла OAB, если известно, что BC – диаметр, а
угол AOC равен 106°. Ответ дайте в градусах.
O
C
487. а) На окружности по разные стороны от диаметра AB взяты точки C и D. A
Найдите угол CDB, если угол CBA равен 45°. Ответ дайте в градусах.
O
C
B
D
C
б) Хорда CD перпендикулярна диаметру AB окружности. Найдите угол
A
CBD, если угол CAB равен 17°. Ответ дайте в градусах.
O
B
D
488. а) Точки A и B делят окружность на две дуги. Найдите величину центрального угла, опирающегося на большую из них, если длины дуг относятся как 4:5. Ответ дайте в градусах.
б) Точки A и B делят окружность на две дуги. Найдите величину центрального угла, опирающегося на меньшую из них, если длины дуг относятся как 11:25. Ответ дайте в градусах.
101
489. а) Найдите вписанный угол, опирающийся на дугу, длина которой равна
1
длины окружности. Ответ дайте в градусах.
3
б) Найдите вписанный угол, опирающийся на дугу, длина которой равна
1
длины окружности. Ответ дайте в градусах.
18
490. а) Точки A и B делят окружность с центром O на две дуги. Найдите длину большей дуги, если
длина меньшей дуги 32 и ∠ AOB =°
60 .
б) Точки A и B делят окружность с центром O на две дуги. Найдите длину меньшей дуги, если
длина большей дуги 24 и ∠ AOB =°
40 .
491. а) В угол C, величина которого 45°, вписана окружность, которая касается
сторон угла в точках A и B, точка O – центр окружности. Найдите угол
AOB. Ответ дайте в градусах.
б) В угол C вписана окружность, которая касается сторон угла в точках A
и B, точка O – центр окружности, ∠ AOB =
128° . Найдите угол C. Ответ
дайте в градусах.
A
O
C
492. а) Касательные в точках A и B к окружности с центром O пересекаются под
углом 164°. Найдите угол CAB. Ответ дайте в градусах.
б) Касательные в точках A и B к окружности с центром O пересекаются под
углом 152°. Найдите угол BAO. Ответ дайте в градусах.
493. а) На окружности отмечены точки A и B так, что
равна 136°. Прямая BC касается окружности в точке B
острый. Найдите угол ABC. Ответ дайте в градусах.
б) На окружности отмечены точки A и B так, что
равна 288°. Прямая BC касается окружности в точке B
острый. Найдите угол ABC. Ответ дайте в градусах.
B
O
A
C
B
меньшая дуга AB
так, что угол ABC
большая дуга AB
так, что угол ABC
A
B
C
494. а) К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус
окружности, если AB = 24, AO = 26.
б) К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус
окружности, если AB = 40, AO = 85.
495. а) Сторона AC треугольника ABC проходит через центр описанной около
B
него окружности. Найдите угол A, если угол C равен 36°. Ответ дайте в
градусах.
A
б) Сторона AC треугольника ABC проходит через центр описанной около
него окружности. Найдите угол C, если угол A равен 52°. Ответ дайте в
градусах.
102
С
496. а) Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите радиус окружности, если AB = 21, BC = 28.
б) Сторона AC треугольника ABC проходит через центр описанной около него окружности.
Найдите радиус окружности, если AB = 15, BC = 36.
497. а) Угол А четырёхугольника ABCD, вписанного в окружность, равен 59°. Найдите угол C этого
четырёхугольника. Ответ дайте в градусах.
б) Угол B четырёхугольника ABCD, вписанного в окружность, равен 87°. Найдите угол D этого
четырёхугольника. Ответ дайте в градусах.
498. а) Четырёхугольник ABCD вписан в окружность. Угол ABC равен 142°, угол CAD равен 63°.
Найдите угол АCD. Ответ дайте в градусах.
б) Четырёхугольник ABCD вписан в окружность. Угол ABC равен 99°, угол CAD равен 42°.
Найдите угол АВD. Ответ дайте в градусах.
499. а) Четырёхугольник ABCD описан около окружности, AB = 6, BC = 13, CD = 17. Найдите AD.
б) Четырёхугольник ABCD описан около окружности, AD = 9, BC = 21, CD = 18. Найдите AB.
500. а) Равнобедренная трапеция с основаниями 11 и 15 описана около окружности. Найдите длину
боковой стороны.
б) Равнобедренная трапеция с основаниями 6 и 26 описана около окружности. Найдите длину
боковой стороны.
A
501. В окружность вписан правильный восьмиугольник ABCDEGFH .
Найдите:
а) ∠ ABC ;
б) ∠ GBE ;
в) ∠ HFA ;
г) ∠ BEH ;
д) ∠ CDG ;
е) ∠ GFC .
H
G
B
C
O
F
D
E
Проверочная работа № 21
Вариант 1
1. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором
AB = BC и ∠ ABC =
102° . Найдите величину угла AOB.
2. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол
ABC, если угол BAC равен 33°.
3. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 119°, угол CAD равен 57°. Найдите угол ABD.
4. Точки A и B делят окружность на две дуги. Найдите величину центрального угла, опирающегося
на большую из них, если длины дуг относятся как 5:13. Ответ дайте в градусах.
5. В угол C, величина которого 36°, вписана окружность, которая касается сторон угла в точках A
и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.
6. Радиус окружности, описанной около квадрата, равен 16 2 . Найдите радиус окружности, вписанной в этот же квадрат.
103
Вариант 2
1. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 75°. Найдите
величину угла BOD.
2. Вписанный острый угол опирается на хорду окружности, равную её радиусу. Найдите градусную
меру этого угла.
3. Точки A и B делят окружность на две дуги. Найдите величину центрального угла, опирающегося
на меньшую из них, если длины дуг относятся как 7:13. Ответ дайте в градусах.
4. К окружности с центром в точке O проведены касательная AB (B – точка касания) и секущая
AO. Найдите радиус окружности, если AB = 8 см, AO = 10 см.
5. В угол C вписана окружность, которая касается сторон угла в точках A и B, точка O – центр
окружности, ∠AOB =132° . Найдите угол C. Ответ дайте в градусах.
6. Радиус окружности, вписанной в квадрат, равен 3 2 . Найдите радиус окружности, описанной
около этого же квадрата.
§ 8. Стереометрия
8.1. Прикладные задачи по стереометрии
502. От деревянной правильной треугольной призмы отпилили все её вершины
(см. рис.). Невидимые рёбра на рисунке не изображены.
а) Сколько вершин у получившегося многогранника?
б) Сколько рёбер у получившегося многогранника?
в) Сколько граней у получившегося многогранника?
503. От деревянной правильной четырёхугольной призмы сделали плоские спилы всех её вершин
(см. рис.). Невидимые рёбра на рисунке не изображены.
а) Сколько вершин у получившегося многогранника?
б) Сколько рёбер у получившегося многогранника?
в) Сколько граней у получившегося многогранника?
504. В деревянном кубике сделали плоский спил так, что его плоскость проходит через точки M и N параллельно боковому ребру. Получилось два многогранника.
а) Сколько вершин имеет получившийся многогранник с большим
N
M
числом граней?
б) Сколько рёбер имеет получившийся многогранник с большим
числом граней?
в) Сколько граней имеет получившийся многогранник с большим
числом граней?
505. В деревянной треугольной призме сделали плоский спил так, что
его плоскость проходит через точки через точки A, B и C (см. рис.)
и разбивает треугольную призму на два многогранника.
а) Сколько вершин у многогранника, имеющего наибольшее число
граней?
б) Сколько рёбер у многогранника, имеющего наибольшее число
граней?
A
в) Сколько граней у многогранника, имеющего наибольшее число
вершин?
104
B
А
C
M
506. В деревянной треугольной пирамиде сделали плоский спил так,
что его плоскость проходит через точки K, M и N (см. рис.) и
разбивает треугольную пирамиду на два многогранника.
а) Сколько вершин имеет получившийся многогранник с большим числом граней?
б) Сколько рёбер имеет получившийся многогранник с большим
числом граней?
в) Сколько граней имеет получившийся многогранник с большим числом граней?
K
N
507. а) Открытую коробку, имеющую форму куба с ребром 40 см, нужно
покрасить снаружи со всех сторон. Найдите площадь поверхности,
которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
б) Открытую коробку, имеющую форму куба с ребром 50 см, нужно
покрасить снаружи со всех сторон. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
508. а) Аквариум имеет форму прямоугольного параллелепипеда с размерами 70 см × 30 см × 45 см.
Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
б) Аквариум имеет форму прямоугольного параллелепипеда с размерами 100 см × 20 см × 70 см.
Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
509. а) Из двух шкатулок, имеющих форму правильной четырёхугольной призмы, первая шкатулка втрое выше
второй, а вторая в три раза шире первой. Во сколько
раз объём второй шкатулки больше объёма первой?
б) Из двух шкатулок, имеющих форму правильной четырёхугольной призмы, первая шкатулка вдвое выше
второй, а вторая в четыре раза шире первой. Во сколько раз объём первой шкатулки меньше
объёма второй?
510. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые).
Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой
детали. Ответ дайте в квадратных сантиметрах.
а)
б)
2
2
2
2
5
1
4
3
6
2
105
в)
г)
3
1
1
5
1
4
5
2
6
1
511. Используя данные задачи 510, найдите объём каждой детали. Ответ дайте в кубических сантиметрах.
512. а) Вода в сосуде, имеющем форму правильной четырёхугольной призмы, находится на уровне h = 126 см. На каком уровне окажется вода,
если её перелить в другой сосуд, имеющий форму правильной четырёхугольной призмы, у которого сторона основания втрое больше, чем у
данного? Ответ дайте в сантиметрах.
б) Вода в сосуде, имеющем форму правильной четырёхугольной призмы, находится на уровне h = 11 см. На каком уровне окажется вода,
если её перелить в другой сосуд, имеющий форму правильной четырёхугольной призмы, у которого сторона основания втрое меньше, чем у
данного? Ответ дайте в сантиметрах.
h
513. а) В сосуд, имеющий форму правильной четырёхугольной призмы со
стороной основания, равной 25 см, налита жидкость. Чтобы измерить
объём камня, его полностью погружают в эту жидкость. Найдите объём
камня, если после его погружения уровень жидкости в сосуде поднялся
на 18 см. Ответ дайте в кубических сантиметрах.
б) В сосуд, имеющий форму правильной четырёхугольной призмы со
стороной основания, равной 15 см, налита жидкость. Чтобы измерить
объём камня, его полностью погружают в эту жидкость. Найдите объём
камня, если после его погружения уровень жидкости в сосуде поднялся
на 24 см. Ответ дайте в кубических сантиметрах.
514. а) Вода в сосуде цилиндрической формы находится на уровне h = 100 см.
На каком уровне окажется вода, если её перелить в другой цилиндрический
сосуд, у которого радиус основания в два с половиной раза больше, чем у
данного? Ответ дайте в сантиметрах.
б) Вода в сосуде цилиндрической формы находится на уровне h = 35 см.
На каком уровне окажется вода, если её перелить в другой цилиндрический
сосуд, у которого радиус основания в два раза меньше, чем у данного?
Ответ дайте в сантиметрах.
106
h
515. а) В сосуд цилиндрической формы, площадь основания которого равна
1200 квадратным сантиметрам, налита жидкость. Чтобы измерить объём
камня, его полностью погружают в эту жидкость. Найдите объём камня,
если после его погружения уровень жидкости в сосуде поднялся на 8 см.
Ответ дайте в кубических сантиметрах.
б) В сосуд цилиндрической формы, площадь основания которого равна
1400 квадратным сантиметрам, налита жидкость. Чтобы измерить объём
камня, его полностью погружают в эту жидкость. Найдите объём камня,
если после его погружения уровень жидкости в сосуде поднялся на 9 см.
Ответ дайте в кубических сантиметрах.
516. а) Трубу цилиндрической формы требуется покрасить снаружи. Найдите площадь
окрашиваемой поверхности, если длина трубы 10 м, внешний обхват трубы
составляет 18 см, а торцы красить не надо. Ответ дайте в квадратных сантиметрах.
б) Трубу цилиндрической формы требуется покрасить снаружи. Найдите площадь
окрашиваемой поверхности, если длина трубы 12 м, внешний обхват трубы
составляет 62 см, а торцы красить не надо. Ответ дайте в квадратных сантиметрах.
517. а) У хозяйки имеется две кастрюли цилиндрической формы. Первая кастрюля в два раза ниже второй, а вторая
вдвое шире первой. Во сколько раз объём второй кастрюли больше объёма первой?
б) У хозяйки имеется две кастрюли цилиндрической формы. Первая кастрюля в три раза ниже второй, а вторая в
полтора раза шире первой. Во сколько раз объём второй
кастрюли больше объёма первой?
518. а) В сосуде, имеющем форму конуса, уровень жидкости достигает
3
высоты, и её объём равен 54 мл. Найдите объём сосуда. Ответ дайте
4
в миллилитрах.
б) В сосуде, имеющем форму конуса, уровень жидкости достигает
3
высоты. Объём сосуда 250 мл. Чему равен объём налитой жидкости?
5
Ответ дайте в миллилитрах.
519. а) Однородный шар диаметром 6 см имеет массу 648 граммов.
Чему равна масса шара, изготовленного из того же материала, с
диаметром 5 см? Ответ дайте в граммах.
б) Однородный шар диаметром 4 см имеет массу 192 грамма. Чему
равна масса шара, изготовленного из того же материала, с диаметром 5 см? Ответ дайте в граммах.
107
Проверочная работа № 22
Вариант 1
1. От деревянной правильной пятиугольной призмы отпилили все её вершины
(см. рис.). Сколько рёбер у получившегося многогранника (невидимые рёбра
на рисунке не изображены)?
2. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые).
Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой
детали. Ответ дайте в квадратных сантиметрах.
4
2
2
5
7
3. У хозяйки имеется две кастрюли цилиндрической формы. Первая кастрюля в полтора раза ниже второй, а вторая втрое шире
первой. Во сколько раз объём второй кастрюли больше объёма
первой?
Вариант 2
1. От деревянной правильной пятиугольной призмы отпилили все её вершины
(см. рис.). Сколько граней у получившегося многогранника (невидимые рёбра
на рисунке не изображены)?
2. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые).
Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой
детали. Ответ дайте в квадратных сантиметрах.
2
9
4
12
2
3. Вода в сосуде цилиндрической формы находится на уровне
h = 72 см. На каком уровне окажется вода, если её перелить
в другой цилиндрический сосуд, у которого радиус основания
в полтора раза больше, чем у данного? Ответ дайте в сантиметрах.
108
h
8.2. Задачи по стереометрии
520. а) Найдите диагональ прямоугольного параллелепипеда, если его измерения равны 2, 3 и 6.
б) Найдите диагональ прямоугольного параллелепипеда, если его измерения равны 6, 6 и 7.
521. а) Найдите ребро куба, если его диагональ равна 10 3 .
б) Найдите диагональ куба, если его ребро равно 10 3 .
522. а) Найдите площадь полной поверхности куба, ребро которого равно 4.
б) Найдите площадь полной поверхности куба, ребро которого равно 5.
523. а) Найдите площадь полной поверхности куба, диагональ грани которого равна 4 2 .
б) Найдите площадь полной поверхности куба, диагональ грани которого равна 6 2 .
524. а) Два ребра прямоугольного параллелепипеда равны 3 и 9, а объём
параллелепипеда равен 351. Найдите площадь полной поверхности этого
параллелепипеда.
б) Два ребра прямоугольного параллелепипеда равны 2 и 13, а объём
параллелепипеда равен 312. Найдите площадь полной поверхности этого
параллелепипеда.
525. а) В прямоугольном параллелепипеде ABCDA1 B1C1 D1 с основанием ABCD рёбра АD, АB и диагональ A1 D боковой грани А1
равны соответственно 4, 12 и 5. Найдите площадь боковой
B1
C1
B
C
D1
поверхности параллелепипеда ABCDA1 B1C1 D1 .
б) В прямоугольном параллелепипеде ABCDA1 B1C1 D1 с основанием ABCD рёбра BC, АB и диагональ BC1 боковой грани
равны соответственно 8, 13 и 17. Найдите площадь боковой
поверхности параллелепипеда ABCDA1 B1C1 D1 .
А
D
B1
526. а) В правильной четырехугольной призме
ABCDA1 B1C1 D1
А1
C1
D1
BA
Ñ11D11 = 4 2 , BD1 = 4 11 . Найдите площадь боковой поверхности призмы.
б) В правильной четырехугольной призме
ABCDA1 B1C1 D1
Ñ11D11 = 5 2 , BD1 = 3 11 . Найдите площадь боковой поверхBA
ности призмы.
B
А
C
D
109
B1
527. а) В правильной треугольной призме ABCA1 B1C1 AB = 5 , AA1 = 13 . Найдите площадь боковой поверхности призмы ABCA1 B1C1 .
А1
C1
б) В правильной треугольной призме ABCA1 B1C1 AB = 15 , AA1 = 17 . Най-
B
дите площадь боковой поверхности призмы ABCA1 B1C1 .
А
C
528. а) Даны два куба, рёбра которых соответственно равны 4 и 2.
Во сколько раз объём большего куба больше объёма меньшего?
б) Даны два куба, рёбра которых соответственно равны 6 и 3.
Во сколько раз объём меньшего куба меньше объёма большего?
B1
529. а) В прямоугольном параллелепипеде ABCDA1 B1C1 D1 рёбра AD, AB и А1
диагональ AD1 боковой грани равны соответственно 5, 15 и 13. Найдите
C1
D1
объём параллелепипеда ABCDA1 B1C1 D1 .
б) В прямоугольном параллелепипеде ABCDA1 B1C1 D1 рёбра AD, CC1 и
диагональ B1D1 основания соответственно 4, 12 и 5. Найдите объём параллелепипеда ABCDA1 B1C1 D1 .
B
А
C
D
B1
530. а) В правильной четырехугольной призме ABCDA1 B1C1 D1 A1C1 = 4 2 ,
А1
C1
D1
BD1 = 4 6 . Найдите объём призмы.
б) В правильной четырехугольной призме ABCDA1 B1C1 D1 A1C1 = 6 2 ,
BD1 = 2 34 . Найдите объём призмы.
B
А
531. а) В основании прямой призмы лежит прямоугольный треугольник, катеты
которого равны 6 и 8. Найдите объём призмы, если её высота равна 10.
б) В основании прямой призмы лежит прямоугольный треугольник, катеты
которого равны 5 и 12. Найдите объём призмы, если её высота равна 13.
110
C
D
532. а) Сторона основания правильной треугольной призмы равна 15, а высота
этой призмы равна 8 3 . Найдите объём призмы.
б) Сторона основания правильной треугольной призмы равна 8, а высота этой
призмы равна 7 3 . Найдите объём призмы.
B1
533. а) В правильной треугольной призме ABCA1 B1C1 AB = 5 , BA1 = 133 . А1
C1
Найдите объем призмы ABCA1 B1C1 .
б) В правильной треугольной призме ABCA1 B1C1 AB = 15 , BA1 = 237 .
Найдите объем призмы ABCA1 B1C1 .
B
А
C
S
534. а) В четырёхугольной правильной пирамиде SABCD, сторона
основания равна 6, высота пирамиды 4. Найти апофему SK .
б) В четырёхугольной правильной пирамиде SABCD, площадь ос-
B
нования S ABCD = 36 , а площадь боковой поверхности пирамиды Sбок = 48. Найдите апофему пирамиды.
C
K
О
А
D
535. а) В четырёхугольной правильной пирамиде SABC, радиус окружности, описанной вокруг основания ABCD, равен R = 3 2 , а площадь боковой поверхности пирамиды Sбок = 48. Найдите
апофему пирамиды.
б) В четырёхугольной правильной пирамиде SABC, площадь боковой поверхности пирамиды
Sбок = 48, а периметр основания равен 24. Найдите апофему пирамиды.
S
536. а) В правильной четырехугольной пирамиде SABCD точка О –
центр основания, S – вершина, SB = 13 , BD = 24 . Найдите высоту пирамиды SO.
б) В правильной четырехугольной пирамиде SABCD точка О –
центр основания, S – вершина, SB = 5 , BD = 8 . Найдите высоту
пирамиды SO.
C
D
О
B
А
111
537. а) В правильной четырехугольной пирамиде SABCD точка О – центр
основания, S – вершина, высота пирамиды CO = 8, диагональ основания BD = 30. Найдите боковое ребро пирамиды.
б) В правильной четырехугольной пирамиде SABCD точка О –
центр основания, S – вершина, высота пирамиды CO = 5, диагональ
основания BD = 24. Найдите боковое ребро пирамиды.
S
C
B
О
D
А
538. а) В правильной четырёхугольной пирамиде SABCD, точка О – центр
основания, S – вершина. Высота пирамиды 48, боковое ребро 60. Найдите диагональ основания пирамиды.
б) В правильной четырёхугольной пирамиде SABCD, точка О – центр
основания, S – вершина. Высота пирамиды 24, боковое ребро 25. Найдите диагональ основания пирамиды.
539. а) Дана правильная треугольная пирамида SABC. Боковое ребро пирамиды
S
равно 13. В основании ABC, со стороной AB = 5 3 , проведена высота
AH. Найдите высоту пирамиды.
б) Дана правильная треугольная пирамида SABC, сторона основания
которой AB = 4 3 , а высота этой пирамиды равна 3. Найдите боковое
ребро SA.
А
.
540. а) Найдите площадь боковой поверхности правильной треугольной пирамиды, стороны основания которой равны 16, а боковые ребра – 10.
б) Найдите площадь боковой поверхности правильной треугольной пирамиды, стороны основания которой равны 18, а боковые ребра – 15.
541. а) Найдите площадь боковой поверхности правильной четырёхугольной
пирамиды, стороны основания которой равны 16, а боковые ребра – 17.
б) Найдите площадь боковой поверхности правильной четырёхугольной
пирамиды, стороны основания которой равны 14, а боковые ребра – 25.
542. а) Найдите площадь боковой поверхности правильной шестиугольной пирамиды, стороны основания которой равны 10, а боковые ребра – 13.
б) Найдите площадь боковой поверхности правильной шестиугольной пирамиды, стороны основания которой равны 14, а боковые ребра – 25.
112
C
H
B
543. а) Основанием четырёхугольной пирамиды является прямоугольник со сторонами 15 и 2. Её
объём равен 40. Найдите высоту пирамиды.
б) Основанием четырёхугольной пирамиды является прямоугольник со сторонами 4 и 3. Её объём равен 22. Найдите высоту пирамиды.
544. а) Дана правильная треугольная пирамида SABC. Площадь основания АВС равна 18, а объём
пирамиды равен 12. Найдите высоту пирамиды.
б) Дана правильная треугольная пирамида SABC. Площадь основания АВС равна 11, объём пирамиды также равен 11. Найдите высоту пирамиды.
545. а) Объём правильной шестиугольной пирамиды 324. Сторона основания
равна 6. Найдите боковое ребро пирамиды.
б) Объём правильной шестиугольной пирамиды 768. Сторона основания
равна 8. Найдите боковое ребро пирамиды.
546. а) Основанием треугольной пирамиды ABCD является треугольник ABC,
DH – высота пирамиды. Найдите объём пирамиды ABCD, если площадь
треугольника ABC равна 12, а DH = 7.
б) Основанием треугольной пирамиды ABCD является равносторонний
треугольник ABC, DH – высота пирамиды. Найдите объём пирамиды
D
S
А
ABCD, если AB = 5, DH = 4 3 .
B
H
C
D
547. а) В треугольной пирамиде ABCD рёбра AB, BC и BD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB = 5, BC = 12 и BD = 7.
б) В треугольной пирамиде ABCD рёбра AB, BC и BD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB = 5, AC = 13 и BD = 10.
C
B
А
548. а) Основанием четырехугольной пирамиды является прямоугольник со сторонами 5 и 9. Объём пирамиды равен 135. Найдите высоту этой пирамиды.
б) Основанием четырехугольной пирамиды является прямоугольник со сторонами 8 и 12. Объём пирамиды равен 216. Найдите
высоту этой пирамиды.
S
E
549. а) Объём правильной четырёхугольной пирамиды SABCD равен
96. Точка E – середина ребра SD. Найдите объём треугольной пирамиды EACD.
D
C
B
А
113
S
б) Объём правильной четырёхугольной пирамиды SABCD равен 48.
Точка E – середина ребра SD, точка F – середина ребра AD. Найдите
объём треугольной пирамиды EBCF.
E
D
C
F
B
А
B1
550. а) Объем куба ABCDA1 B1C1 D1 равен 108. Найдите объем пирамиды
C1
D1
А1
OABCD, где точка O – центр грани CC1 D1 D.
O
B
C
А
D
B1
А1
C1
O
D1
б) Объем куба ABCDA1 B1C1 D1 равен 96. Найдите объем пирамиды
OABCD, где точка O – центр грани A1 B1C1 D1 .
B
А
C
D
551. а) Радиус основания цилиндра равен 25, а его образующая равна 8. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24.
Найдите площадь этого сечения.
б) Радиус основания цилиндра равен 17, а его образующая равна 5. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 15.
Найдите площадь этого сечения.
552. а) Даны два цилиндра. Радиус основания и высота первого цилиндра
равны соответственно 10 и 12, а второго – 4 и 6. Во сколько раз
объём первого цилиндра больше объёма второго?
б) Даны два цилиндра. Радиус основания и высота первого цилиндра
равны соответственно 6 и 4, а второго – 8 и 9. Во сколько раз объём
второго цилиндра больше объёма первого?
553. а) Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 10
и 12, а второго – 4 и 6. Во сколько раз площадь боковой поверхности первого цилиндра больше
боковой поверхности второго?
б) Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 12 и
8, а второго – 16 и 18. Во сколько раз площадь боковой поверхности второго цилиндра больше
боковой поверхности первого?
554. а) Высота конуса равна 16, а диаметр основания равен 60. Найдите длину
образующей конуса.
б) Найдите высоту конуса, если его образующая равна 13, а радиус основания 5.
114
555. а) Диаметр основания конуса равен 32, а длина образующей равна 20. Найдите площадь осевого
сечения этого конуса.
б) Диаметр основания конуса равен 42, а длина образующей равна 75. Найдите высоту конуса.
556. а) Даны два конуса. Радиус основания и высота первого конуса
равны соответственно 10 и 12, а второго – 4 и 6. Во сколько раз
объём первого конуса больше объёма второго?
б) Даны два конуса. Радиус основания и высота первого конуса
равны соответственно 6 и 4, а второго – 8 и 9. Во сколько раз
объём второго конуса больше объёма первого?
557. а) Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 10
и 14, а второго – 4 и 5. Во сколько раз площадь боковой поверхности первого конуса больше
боковой поверхности второго?
б) Даны два конуса. Радиус основания и высота первого конуса равны соответственно 12 и 8, а
второго – 16 и 18. Во сколько раз площадь боковой поверхности второго конуса больше боковой
поверхности первого?
558. Объем конуса равен 300π , а его высота равна 9. Найдите радиус основания
конуса.
б) Объем конуса равен 64π , а его радиус основания равен 8. Найдите высоту
конуса..
559. а) Объём конуса равен 216. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
б) Объём конуса равен 128. Через точку делящую высоту конуса в отношении
3:1, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
560. а) Даны два шара. Радиусы первого и второго шаров соответственно равны 4 и 12. Во сколько раз объём второго шара
больше объёма первого?
б) Даны два шара. Радиусы первого и второго шаров соответственно равны 64 и 256. Во сколько раз объём первого шара
меньше объёма второго?
561. а) Даны два шара с радиусами 64 и 128. Во сколько раз площадь поверхности большего шара
больше площадь поверхности меньшего?
б) Даны два шара с радиусами 25 и 125. Во сколько раз площадь поверхности большего шара
больше площадь поверхности меньшего?
115
Проверочная работа № 23
Вариант 1
1. Стороны основания прямоугольного параллелепипеда равны 6 и 9, а объём параллелепипеда
равен 216. Найдите площадь боковой поверхности этого параллелепипеда.
2. В основании прямой призмы лежит прямоугольный треугольник, один из катетов
которого равен 15, а гипотенуза равна 17. Найдите объём призмы, если её высота равна 10.
3. Найдите объём правильной четырёхугольной пирамиды, сторона основания
которой равна 6, а боковое ребро равно
43 .
4. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 14 и
30, а второго – 7 и 12. Во сколько раз площадь боковой поверхности первого цилиндра больше
боковой поверхности второго?
Вариант 2
1. Стороны основания прямоугольного параллелепипеда равны 3 и 12, а объём параллелепипеда
равен 216. Найдите площадь боковой поверхности этого параллелепипеда.
2. В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 7, а гипотенуза равна
её высота равна 9.
113 . Найдите объём призмы, если
3. Найдите объём правильной четырёхугольной пирамиды, сторона основания
которой равна 8, а боковое ребро равно 2 17 .
4. Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 18 и
20, а второго – 6 и 12. Во сколько раз площадь боковой поверхности первого конуса больше
боковой поверхности второго?
116
Глава 3. тренИровочные варианты
ВАРИАНТ № 1
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
На автомобиле установлены колёса с дисками, диаметр которых равен 16 дюймам. Выразите
диаметр дисков в миллиметрах, если в одном дюйме 2,54 см.
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) масса мотоцикла
1) 12 ц
Б) масса книги
2) 130 кг
В) масса жирафа
3) 9,98 г
Г) масса листа бумаги
4) 0,25 кг
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показана среднемесячная температура в некотором городе с января по декабрь.
По вертикали указана температура в градусах Цельсия, а по горизонтали – номер месяца
t°C
24
21
18
15
12
9
6
3
0
–3
–6
–9
–12
–15
–18
–21
1 2 3 4 5 6 7 8 9 10 11 12 номер
месяца
Определите по диаграмме наибольшую среднемесячную температуру в рассматриваемом городе
в первой половине года. Ответ дайте в градусах Цельсия.
Ответ: ___________
117
4
В службе такси рассчитывают стоимость поездки, начиная с третьей минуты, по формуле
R = 320 + 8(t − 2) , где R – стоимость поездки (в рублях), t – время поездки в минутах. Найдите
продолжительность поездки в минутах, если её стоимость составила 984 рублей?
Ответ: ___________
5
Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 4. Результат округлите до десятых.
Ответ: ___________
6
Для ремонта в ванной комнате необходимо купить 95 плиток. Размер одной плитки 20 см × 20 см.
Плитку можно приобрести в одной из двух фирм. Стоимость плитки и доставки приведены в
таблице.
Стоимость 1 м2
плитки (руб.)
Стоимость
доставки (руб.)
А
1900
2000
Б
2300
1000
Дополнительные условия
при стоимости заказа более
7000 рублей скидка на заказ 10 %
при стоимости заказа более
8000 рублей доставка бесплатно
Сколько рублей составит самый дешёвый вариант покупки с учётом доставки?
Ответ: ___________
7
На рисунке изображены графики функций вида =
y kx + b . Установите соответствие между графиками этих функций и значениями их производной в точке x =2.
Графики
ГРАФИКИ
ГРАФИКИ
ГРАФИКИ
ГРАФИКИ
А)
А)
А)
А)А)
Б)
Б)
Б)Б)Б)
yy y y
yy y y
11 1 1
xx x x
0 0 01101 1
Г)
yy y y
11 1 1
0 0 01101 1
xx x x
Г)
Г)Г)Г)
yy y y
11 1 1
0 0 01101 1
В)
В)
В)
В)В)
11 1 1
xx x x
0 0 01101 1
Значения производной
2) 2
1) –2
3) 0,5
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
118
А
Б
В
Г
4) 0
xx x x
8
Фирма приобрела стол, компьютерный стул, сканер и принтер. Известно, что принтер дороже
сканера, а компьютерный стул дороже сканера и дешевле стола. Выберите утверждения, которые
верны при указанных условиях.
1) Компьютерный стул дешевле принтера.
2) Сканер дешевле всех покупок.
3) Принтер дороже всех покупок.
4) Стол дороже сканера.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
План местности разбит на клетки. Каждая клетка обозначает
квадрат 1 м × 1 м. Найдите площадь участка, изображённого
на плане. Ответ дайте в квадратных метрах.
Ответ: ___________
1м
10
Дачный участок имеет форму прямоугольника, а его стороны равны 47 м и 26 м. Одна из
меньших сторон идёт вдоль реки, а три остальные стороны нужно обнести забором. Найдите
длину забора. Ответ дайте в метрах.
Ответ: ___________
11 В цилиндрическом сосуде уровень жидкости достигает 36 см.
На какой высоте будет находиться уровень жидкости, если ее
перелить во второй сосуд, диаметр которого в 3 раза больше
первого? Ответ дайте в сантиметрах.
Ответ: ___________
12 Диагональ прямоугольника образует с одной из его сторон угол 56°. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Ответ: ___________
13 Объём конуса равен 12π, а его высота равна 4. Найдите радиус основания конуса.
Ответ: ___________
119
14 Найдите значение выражения 0,05 ⋅ 0,0005 ⋅ 5000000 .
Ответ: ___________
15 В классе девочек в 7 раз больше, чем мальчиков. Сколько процентов всех учащихся этого класса
составляют мальчики?
Ответ: ___________
16 Найдите значение выражения −11 2 cos855° .
Ответ: ___________
1
17 Найдите корень уравнения
25
Ответ: ___________
−x
= 125.
18 Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит.
Установите соответствие между числами и отрезками из правого столбца.
ЧИСЛА
ОТРЕЗКИ
А) log 6 39
1) [1; 2]
Б) 0, 23
2) [ 2; 3]
71
59
Г) 11
В)
3) [3; 4 ]
4) [ 4; 5]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите трёхзначное число, все цифры которого различны, а остатки от деления этого числа
на 3, 5 и 11 равны 2. В ответе укажите какое-нибудь одно такое число.
Ответ: ___________
20
Имеется два раствора кислоты с концентрациями 50% и 45%. Если их слить в один сосуд,
получится раствор массой 4 кг, содержащий 48% кислоты. Найдите массу второго раствора.
Ответ дайте в килограммах.
Ответ: ___________
21 Тринадцать домов соединены между собой проводами так, что от каждого дома отходит ровно
8 проводов. Сколько всего проводов протянуто между этими тринадцатью домами?
Ответ: ___________
!
120
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 2
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
На автомобиле установлены колёса с дисками, диаметр которых равен 14 дюймам. Выразите
диаметр дисков в миллиметрах, если в одном дюйме 2,54 см.
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) масса ноутбука
1) 36 г
Б) масса браслета
2) 180 г
В) масса металлической двери
3) 2,5 кг
Г) масса блюдца
4) 0,75 ц
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показана среднемесячная температура в некотором городе с января по декабрь.
По вертикали указана температура в градусах Цельсия, а по горизонтали – номер месяца.
t°C
24
21
18
15
12
9
6
3
0
–3
–6
–9
–12
–15
–18
–21
1 2 3 4 5 6 7 8 9 10 11 12 номер
месяца
Определите по диаграмме наибольшую среднемесячную температуру в рассматриваемом городе
в первом квартале года. Ответ дайте в градусах Цельсия.
Ответ: ___________
121
4
В службе такси рассчитывают стоимость поездки, начиная с шестой минуты, по формуле
R = 390 + 8(t − 5) , где R – стоимость поездки (в рублях), t – время поездки в минутах. Найдите
продолжительность поездки в минутах, если её стоимость составила 1126 рублей?
Ответ: ___________
5
Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число,
меньшее 4. Результат округлите до десятых.
Ответ: ___________
6
Для ремонта в ванной комнате необходимо купить 39 плиток. Размер одной плитки 50 см × 50 см.
Плитку можно приобрести в одной из двух фирм. Стоимость плитки и доставки приведены в
таблице.
Стоимость 1 м2
плитки (руб.)
Стоимость
доставки (руб.)
А
2200
2000
Б
2400
1000
Дополнительные условия
при стоимости заказа более 20000 рублей
скидка на заказ 10 %
при стоимости заказа более 8000 рублей
доставка бесплатно
Сколько рублей составит самый дешёвый вариант покупки с учётом доставки?
Ответ: ___________
7
На рисунке изображены графики функций вида =
y kx + b . Установите соответствие между
графиками этих функций и значениями их производной в точке x = –3.
ГРАФИКИ
ГРАФИКИ
ГРАФИКИ
ГРАФИКИ
Графики
А)
А)А)А)
А)
Б)Б)Б)Б)
Б)
В)
В)В)В)
В)
Г)Г)Г)Г)
Г)
yy y y
yy y y
yy y y
yy y y
11 1 1
11 1 1
11 1 1
11 1 1
0 0 101 01 1
0 0 101 01 1
0 0 101 01 1
xx x x
xx x x
xx x x
0 0 101 01 1
Значения производной
1) –3
2) 1/3
3) –5
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
122
А
Б
В
Г
4) 0,5
xx x x
8
Фирма приобрела шкаф, компьютер, клавиатуру и принтер. Известно, что принтер дешевле компьютера, а шкаф дороже клавиатуры и дешевле компьютера. Выберите утверждения, которые
верны при указанных условиях.
1) Клавиатура дешевле принтера.
2) Принтер дороже шкафа.
3) Компьютер дороже всех покупок.
4) Клавиатура дешевле компьютера.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
План местности разбит на клетки. Каждая клетка обозначает квадрат
1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ
дайте в квадратных метрах.
Ответ: ___________
1м
10 Д
ачный участок имеет форму прямоугольника, а его стороны равны 51 м и 27 м. Одна из больших сторон идёт вдоль реки, а три остальные стороны нужно обнести забором. Найдите длину
забора. Ответ дайте в метрах.
Ответ: ___________
11
В цилиндрическом сосуде уровень жидкости достигает 48 см.
На какой высоте будет находиться уровень жидкости, если ее
перелить во второй сосуд, диаметр которого в 4 раза больше
первого? Ответ дайте в сантиметрах.
Ответ: ___________
12 Диагональ прямоугольника образует с одной из его сторон угол 38°. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Ответ: ___________
13
Объём конуса равен 49π, а его высота равна 3. Найдите радиус основания
конуса.
Ответ: ___________
123
14
Найдите значение выражения 0,0004 ⋅ 400000 ⋅ 0,004 .
Ответ: ___________
15 В магазин привезли яблоки и груши, причём яблок привезли в 4 раза меньше, чем груш. Сколько
процентов всех привезённых фруктов составили яблоки?
Ответ: ___________
16
Найдите значение выражения −14 3 tg 780° .
Ответ: ___________
4
17 Найдите корень уравнения
9
Ответ: ___________
−x
= 2, 25 .
18 Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит.
Установите соответствие между числами и отрезками из правого столбца.
ЧИСЛА
ОТРЕЗКИ
31
7
Б) log 3 10
1) [1; 2]
А)
В)
15
Г) 0,99−1
2) [ 2; 3]
3) [3; 4 ]
4) [ 4; 5]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите трёхзначное число, все цифры которого различны, а остатки от деления этого числа
на 2, 7 и 13 равны 1. В ответе укажите какое-нибудь одно такое число.
Ответ: ___________
20
Имеется два раствора кислоты с концентрациями 80% и 40%. Если их слить в один сосуд,
получится раствор массой 5 кг, содержащий 72% кислоты. Найдите массу второго раствора.
Ответ дайте в килограммах.
Ответ: ___________
21 Двенадцать домов соединены между собой проводами так, что от каждого дома отходит ровно
три провода. Сколько всего проводов протянуто между этими двенадцатью домами?
Ответ: ___________
!
124
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 3
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Участников конференции размещают в коттеджах, в каждом из которых можно поселить до
12 человек. Сколько коттеджей надо подготовить, если заявки на участие подали 178 научных
сотрудников и 135 студентов?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) объём чайника
Б) объём бочки
В) объём Тихого океана
Г) объём вагона
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 492 л
2) 1700 см3
3) 120 м3
4) 714·106 км3
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показана среднемесячная температура в некотором городе с января по декабрь.
По вертикали указана температура в градусах Цельсия, а по горизонтали – номер месяца.
t°C
24
21
18
15
12
9
6
3
0
–3
–6
–9
–12
–15
–18
–21
1 2 3 4 5 6 7 8 9 10 11 12 номер
месяца
Определите по диаграмме наименьшую среднемесячную температуру в рассматриваемом городе
в течение года. Ответ дайте в градусах Цельсия.
Ответ: ___________
125
4
Используя формулу hc = xy , где hc – высота прямоугольного треугольника, проведённая к
гипотенузе (в сантиметрах), x, y – проекции катетов на гипотенузу (в сантиметрах), найдите
длину проекции x в сантиметрах, если высота, проведённая к гипотенузе, равна 25 см, а вторая
проекция – 50 см.
Ответ: ___________
5
Случайным образом выбрано двузначное число. Найдите вероятность того, что оно делится
на 8. Результат округлите до сотых.
Ответ: ___________
6
Татьяна хочет заказать очки в одном из трёх магазинов. Ей необходимы двое очков. Цены, предлагаемые магазинами, представлены в таблице. Оплата доставки не входит в стоимость заказа.
Оправа
(руб.)
Линзы
(руб. за 2 шт.)
Доставка
(руб.)
А
3950
2550
580
Б
4300
1910
480
В
4180
2360
500
Дополнительные условия
при заказе стоимостью более 12000 рублей
скидка на заказ 10%
при заказе стоимостью более 12000 рублей
скидка на заказ и доставку 15%
при заказе стоимостью более 12000 рублей
доставка бесплатно
В каком магазине покупка (заказ + доставка) очков будет наиболее выгодной? В ответе укажите
стоимость такой покупки в рублях.
Ответ: ___________
7
Установите соответствие между функциями и характеристиками этих функций на отрезке [ 0; 3] .
ФУНКЦИИ
ХАРАКТЕРИСТИКИ ФУНКЦИИ
y ( x − 2) 2
А) =
1) функция возрастает на отрезке [ 0; 3]
Б) y =
−2 x + 5
2) функция убывает на отрезке [ 0; 3]
2
В) y =
−x + 2x
3) функция имеет точку максимума на отрезке [ 0; 3]
Г) =
y 5x + 1
4) функция имеет точку минимума на отрезке [ 0; 3]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
В понедельник в больницу поступили 40 человек, из них у 20 человек была повышена температура тела, а у 30 человек – боль в горле. У каждого поступившего есть хотя бы один из данных
симптомов заболеваний. Выберите утверждения, которые верны при указанных условиях.
1) У 10 человек из поступивших в понедельник в больницу была повышена температура и
боль в горле одновременно.
126
2) Каждый день в больницу поступает не меньше 40 человек.
3) В больницу всегда поступает больше людей с болью в горле больше, чем с повышенной
температурой тела.
4) У четверти людей, поступивших в понедельник в больницу, была повышена температура
тела, но не было боли в горле.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
План местности разбит на клетки. Каждая клетка обозначает квадрат
1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ
дайте в квадратных метрах.
Ответ: ___________
1м
10
Расстояние между стволами деревьев, высота которых 5 м и 8 м, равно
4 м. Найдите расстояние между верхушками деревьев. Ответ дайте в
метрах.
Ответ: ___________
11
Однородный шар диаметром 2 см имеет массу 88 граммов.
Чему равна масса шара, изготовленного из того же материала, с диаметром 3 см? Ответ дайте в граммах.
Ответ: ___________
12
В треугольнике PMK биссектрисы углов P и M пересекаются в точке O. Найдите ∠ POM , если
∠ PMK =°
64 , ∠ MPK =°
58 . Ответ дайте в градусах.
Ответ: ___________
13
Стороны основания правильной треугольной пирамиды равны 12,
а боковые рёбра равны 10. Найдите площадь боковой поверхности
пирамиды.
Ответ: ___________
127
14 Найдите значение выражения 23,06 − 14,9 .
0,3
Ответ: ___________
15 Пакет молока стоит в магазине 136 рублей. Сколько рублей будет стоить этот пакет молока с
25–процентной скидкой?
Ответ: ___________
16
Найдите значение выражения (12 + 94) ⋅ ( 94 − 12) .
Ответ: ___________
17 Найдите корень уравнения log 7 (2 x − 1) =.
2
Ответ: ___________
18 Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого
столбца. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
2
1) ( −3; 1)
2
2) ( −∞; 1) ( 3; + ∞ )
А) x + 4 x + 3 < 0
Б) x − 4 x + 3 > 0
2
В) x + 2 x − 3 < 0
2
Г) x − 2 x − 3 > 0
3) ( −∞; −1) ( 3; + ∞ )
4) (–3; –1)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите четырёхзначное число, большее 3500, но меньшее 3800, которое делится на 36 и сумма цифр которого равна 18, при этом все цифры искомого числа различны. В ответе укажите
какое-нибудь одно такое число.
Ответ: ___________
20
Первые 150 км автомобиль ехал со скоростью 75 км/ч, следующие 255 км – со скоростью
85 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Ответ: ___________
21 На поверхности глобуса проведены 19 параллелей, включая экватор, и 24 меридиана. На сколько
частей проведённые линии разделили поверхность глобуса?
Ответ: ___________
!
128
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 4
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Участников конференции размещают в коттеджах, в каждом из которых можно поселить до
17 человек. Сколько коттеджей надо подготовить, если заявки на участие подали 145 научных
сотрудников и 113 студентов?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) объём шкатулки
Б) объём чашки
В) объём озера Байкал
Г) объём парного отделения
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1)
2)
3)
4)
240 см3
23 615 км3
23 м3
250 мл
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показана среднемесячная температура в некотором городе с января по декабрь.
По вертикали указана температура в градусах Цельсия, а по горизонтали – номер месяца.
t°C
24
21
18
15
12
9
6
3
0
–3
–6
–9
–12
–15
–18
–21
1 2 3 4 5 6 7 8 9 10 11 12 номер
месяца
Определите по диаграмме наибольшую среднемесячную температуру в рассматриваемом городе
в третьем квартале года. Ответ дайте в градусах Цельсия.
Ответ: ___________
129
4
Используя формулу hc = xy , где hc – высота прямоугольного треугольника, проведённая к
гипотенузе (в сантиметрах), x, y – проекции катетов на гипотенузу (в сантиметрах), найдите
длину проекции x в сантиметрах, если высота, проведённая к гипотенузе, равна 12 см, а вторая
проекция – 48 см.
Ответ: ___________
5
Случайным образом выбрано двузначное число. Найдите вероятность того, что оно делится на 9.
Результат округлите до десятых.
Ответ: ___________
6
Галина решила заказать очки в одном из трёх магазинов. Ей необходимы двое очков. Цены,
предлагаемые магазинами, представлены в таблице.
Оправа (руб.)
Линзы
(руб. за 2 шт.)
Доставка
(руб.)
Дополнительные условия
А
4860
2170
600
при заказе стоимостью более 12000
рублей скидка на заказ и доставку 15%
Б
4250
2050
500
при заказе стоимостью более 12000
рублей доставка бесплатно
В
5130
1980
700
при заказе стоимостью более 12000
скидка на заказ 20%
В каком магазине покупка (заказ + доставка) очков будет наиболее выгодной? В ответе укажите
стоимость такой покупки в рублях.
Ответ: ___________
7
Установите соответствие между функциями и характеристиками этих функций на отрезке
[–4; –1].
ФУНКЦИИ
ХАРАКТЕРИСТИКИ ФУНКЦИИ
1) функция возрастает на отрезке [– 4; – 1]
А) y =
−( x + 2) 2
2
2) функция убывает на отрезке [– 4; – 1]
Б) y = −
x
3) функция имеет точку максимума на отрезке [– 4; – 1]
y x 2 + 3x
В) =
3
4) функция имеет точку минимума на отрезке [– 4; – 1]
Г) y =
x
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
130
А
Б
В
Г
В среду в больницу поступили 50 человек, из них у 25 человек была боль в животе, а
у 30 человек – повышена температура тела. У каждого поступившего есть хотя бы один из данных симптомов заболеваний. Выберите утверждения, которые верны при указанных условиях.
1) По средам в больницу всегда поступают люди с болью в животе.
2) У 10% людей, поступивших в среду в больницу, была боль в животе и повышена температура одновременно.
олько у 25 человек из числа людей, поступивших в среду в больницу, была повышена
3) Т
температура тела, но не болел живот.
4) В среду в больницу поступило больше людей с болью в животе, чем с повышенной температурой тела.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
План местности разбит на клетки. Каждая клетка обозначает квадрат
1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ
дайте в квадратных метрах.
Ответ: ___________
1м
10 Расстояние между стволами деревьев, высота которых 7 м и 13 м, равно
8 м. Найдите расстояние между верхушками деревьев. Ответ дайте в
метрах.
Ответ: ___________
11 Однородный шар диаметром 4 см имеет массу 192 грамма.
Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
Ответ: ___________
12
В треугольнике ABC биссектрисы углов A и B пересекаются в точке S. Найдите ∠ BSA , если
∠ ABC =°
50 , ∠ CAB =
72° . Ответ дайте в градусах.
Ответ: ___________
13
Стороны основания правильной треугольной пирамиды равны 24,
а боковые рёбра равны 20. Найдите площадь боковой поверхности
пирамиды.
Ответ: ___________
14
Найдите значение выражения
17,04 − 12,3
.
0,6
Ответ: ___________
131
15 Пакет молока стоит в магазине 175 рублей. Сколько рублей будет стоить этот пакет молока с
20-процентной скидкой?
Ответ: ___________
16
Найдите значение выражения (8 − 43) ⋅ ( 43 + 8) .
Ответ: ___________
17
Найдите корень уравнения log 3 (3 − 2 x) =
4.
Ответ: ___________
18 Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого
столбца. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А) x 2 + 6 x + 5 > 0
2
Б) x − 6 x + 5 < 0
2
В) x + x − 6 > 0
Г) x 2 − x − 6 < 0
РЕШЕНИЯ
1) (1; 5 )
2) ( −∞; − 3) ( 2; + ∞ )
3) ( −∞; − 5 ) ( −1; + ∞ )
4) ( −2; 3)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите четырёхзначное число, большее 3200, но меньшее 4000, которое делится на 75 и сумма цифр которого равна 24, при этом все цифры искомого числа различны. В ответе укажите
какое-нибудь одно такое число.
Ответ: ___________
20
Первые 240 км автомобиль ехал со скоростью 80 км/ч, следующие 285 км – со скоростью
95 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Ответ: ___________
21 На поверхности глобуса проведены 10 параллелей, включая экватор, и 14 меридианов. На сколько
частей проведённые линии разделили поверхность глобуса?
Ответ: ___________
!
132
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 5
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Расход бензина автомобиля Лизы на 100 км составляет 7,4 л. Стоимость одного литра бензина
равна 54 рубля. Город N находится на расстоянии 450 км от города Лизы. Сколько рублей на
бензин потратит Лиза на поездку в город N? Результат округлите до целых.
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) длина Великой Китайской стены
Б) длина шторы
В) длина ступни человека
Г) длина ремня
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 240 см
2) 1150 мм
3) 21196 км
4) 25 см
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На рисунке жирными точками показана цена одной акции некоторой компании каждый день
с 3 марта по 9 марта 2023 года. По вертикали указана цена акции в рублях, а по горизонтали
число месяца. Для наглядности точки соединены линиями.
395
390
385
3 4 5 6 7 8 9
Используя рисунок, определите цену одной акции указанной фирмы в рублях 9 марта 2023 года.
Ответ: ___________
4
Используя формулу длины окружности C = 2πR , где C – длина окружности (в метрах), R – её
радиус (в метрах), найдите радиус окружности, если её длина равна 237 м. (Считать π = 3).
Ответ: ___________
5
У учителя физики в шкафу книг по математике в 7 раз меньше, чем книг по физике. Найдите вероятность
того, что случайно выбранная книга из его шкафа будет по физике.
Ответ: ___________
133
6
Для озеленения школьной территории необходимо закупить по 13 саженцев спиреи и чубушника венечного, а также по 5 саженцев берёз пушистых и клёнов остролистных. Заказ можно
сделать в одной из двух фирм А и Б.
Деревья (руб./шт.)
Фирма
Кустарники (руб./шт.)
Берёза
Клён
Туя
пушистая остролистный западная
Доставка
Можжевельник
обыкновенный
Чубушник
венечный
Спирея
А
12480
11570
18000
3800
1200
550
Б
13900
12380
19000
4200
1800
600
20% от
стоимости
заказа
15% от
стоимости
заказа
Сколько рублей придётся заплатить за самый дешёвый вариант заказа с доставкой?
Ответ: ___________
7
На рисунке изображён график функции y = f(x). Точки a, b, c, d и e задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции
или её производной.
y
a0
ИНТЕРВАЛЫ
А)
Б)
В)
Г)
1)
2)
3)
4)
(a; b)
( b; c)
(c; d )
( d ; e)
значение
значение
значение
значение
b
c d
e
x
ХАРАКТЕРИСТИКИ
функции положительно в каждой точке интервала.
функции отрицательно в каждой точке интервала.
производной функции положительно в каждой точке интервала.
производной функции отрицательно в каждой точке интервала.
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Лена моет полы каждое воскресенье, а у Жени дома живут крысы, поэтому она всегда моет полы
во вторник, четверг и субботу. Выберите утверждения, которые верны при указанных условиях.
1) Каждая из девочек моет полы хотя бы один раз в неделю.
2) Лена и Женя подруги.
3) Женя моет полы не реже трёх раз в неделю.
4) У Лены нет дома домашних животных.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
134
Г
9
План местности разбит на клетки. Каждая клетка обозначает квадрат
1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ
дайте в квадратных метрах.
Ответ: ___________
1м
10 На какой высоте находится верхний край лестницы, приставленной к стене дома, если её нижний край находится от стены на расстоянии 2 м, а угол наклона лестницы к земле равен 45°?
Ответ дайте в метрах.
Ответ: ___________
11 Даны две кастрюли цилиндрической формы. Первая кастрюля в два раза ниже второй, а вторая втрое шире
первой. Во сколько раз объём второй кастрюли больше
объёма первой?
Ответ: ___________
12
Найдите градусную меру угла OAB, если известно, что BC – диаметр,
а угол AOC равен 106°. Ответ дайте в градусах.
Ответ: ___________
A
B
O
C
13
Сторона основания правильной треугольной призмы ABCA1B1C1
А1
B1
равна 5, а высота этой призмы равна 16 3 . Найдите объём призмы ABCA1B1C1.
Ответ: ___________
А
7,8 ⋅ 1, 4
14 Найдите значение выражения
.
2,1
Ответ: ___________
15
C1
C
B
После уплаты налога 13% Мария получила зарплату 78300 рублей. Сколько рублей составляет
зарплата Марии до уплаты налогов?
Ответ: ___________
16 Найдите значение выражения
(4−15 )5 ⋅ 459
.
4−14
Ответ: ___________
135
17 Найдите корень уравнения 2 x 2 + 2 x − 3 =.
x Если уравнение имеет более одного корня, то в
ответе укажите меньший из них.
Ответ: ___________
18 Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого
столбца. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
−3
А)
>0
x +1
Б) log 4 x > 0
В) 5
Г)
−x
>1
x
<0
x −1
РЕШЕНИЯ
1) ( −∞; 0 )
2) ( −∞; − 1)
3) (1; + ∞ )
4) (0; 1)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите четырёхзначное число, большее 2700, но меньшее 3000, которое делится на 48 и сумма цифр которого равна 24, при этом все цифры искомого числа различны. В ответе укажите
какое-нибудь одно такое число.
Ответ: ___________
20 Расстояние между пристанями А и В равно 38,5 км. Из А в В по течению реки отправился
плот, а через час вслед за ним отправился катер, который, прибыв в пункт В, тотчас повернул
обратно и возвратился в А. К этому времени плот прошёл 22 км. Найдите скорость катера в
стоячей воде, если скорость течения реки равна 4 км/ч.
Ответ: ___________
21 Жук передвигается вдоль координатной прямой в любом направлении на единичный отрезок за
один ход. Сколько существует различных точек на координатной прямой, в которых жук может
оказаться, сделав ровно 11 ходов, стартуя из начала координат?
Ответ: ___________
!
136
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 6
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Расход бензина автомобиля Никиты на 100 км составляет 8,5 л. Стоимость одного литра бензина
равна 59 рубля. Город N находится на расстоянии 380 км от города Никиты. Сколько рублей на
бензин потратит Никита на поездку в город N? Результат округлите до целых.
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) длина стола
1) 12 мм
Б) длина канала им. Москвы
В) длина спички
Г) длина ресницы
2) 128 км
3) 1200 мм
4) 0,04 м
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На рисунке жирными точками показана цена одной акции некоторой компании каждый день
с 3 марта по 9 марта 2023 года. По вертикали указана цена акции в рублях, а по горизонтали
число месяца. Для наглядности точки соединены линиями.
395
390
385
3 4 5 6 7 8 9
Используя рисунок, определите цену одной акции указанной фирмы в рублях 4 марта 2023 года.
Ответ: ___________
4
Используя формулу длины окружности C = 2πR , где C – длина окружности (в метрах), R – её
радиус (в метрах), найдите радиус окружности, если её длина равна 183 м. (Считать π = 3.)
Ответ: ___________
5
У учителя математики в шкафу книг по математике в 24 раза больше, чем книг по истории.
Найдите вероятность того, что случайно выбранная книга из его шкафа будет по истории.
Ответ: ___________
137
6
Для озеленения школьной территории необходимо закупить по 12 саженцев спиреи и чубушника
венечного, а также по 9 саженцев туй западных и клёнов остролистных. Заказ можно сделать
в одной из двух фирм А и Б.
Деревья (руб./шт.)
Кустарники (руб./шт.)
Берёза
Клён
Туя
Можжевельник Чубушник
Фирма
Спирея
пушистая остролистный западная обыкновенный венечный
А
13580
12690
14100
2900
1360
820
Б
10300
11870
13200
3500
1720
700
Доставка
12% от стоимости заказа
25% от стоимости заказа
Сколько рублей придётся заплатить за самый дешёвый вариант заказа с доставкой?
Ответ: ___________
7
На рисунке изображён график функции y = f(x). Точки a, b, c, d и e задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции
или её производной.
y
a 0
ИНТЕРВАЛЫ
b
c
d
e
x
ХАРАКТЕРИСТИКИ
А) (a; b)
1)
2)
3)
4)
Б) ( b; c)
В) (c; d )
Г) (d ; e)
функция имеет точку максимума на интервале
функция имеет точку минимума на интервале
значение производной функции положительно в каждой точке интервала
значение производной функции отрицательно в каждой точке интервала
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
138
А
Б
В
Г
У Надежды двое детей, а у Елены есть сын. Надеждина дочка Соня ходит в детский сад, а
Сонин единственный родной брат Артём учится в университете. Сыну Елены Даниле – 16 лет.
Выберите утверждения, которые верны при указанных условиях.
1) Данила старше Сони.
2) У Надежды есть сын.
3) Данила учится в школе.
4) У Елены только один ребёнок.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
План местности разбит на клетки. Каждая клетка обозначает квадрат
1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ
дайте в квадратных метрах.
Ответ: ___________
1м
10 На какой высоте находится верхний край лестницы, приставленной к стене дома, если её нижний край находится от стены на расстоянии
3 м, а угол наклона лестницы к земле равен 60°?
Ответ дайте в метрах.
Ответ: ___________
11 Даны две кастрюли цилиндрической формы. Первая кастрюля в два с половиной раза ниже второй, а вторая
вдвое шире первой. Во сколько раз объём второй кастрюли больше объёма первой?
Ответ: ___________
12 Найдите градусную меру центрального угла AOB, если известно, что
BC – диаметр, а угол ABC равен 20°. Ответ дайте в градусах.
Ответ: ___________
B
A
O
C
13
Сторона основания правильной треугольной призмы ABCA1B1C1
А1
равна 2, а высота этой призмы равна 10 3 . Найдите объём
C1
B1
призмы ABCA1B1C1.
А
14 Найдите значение выражения
3,6 ⋅ 9,5
.
4,5
C
B
Ответ: ___________
15 После уплаты налога 13 % Кирилл получил зарплату 104400 рублей. Сколько рублей составляет
зарплата Кирилла до уплаты налогов?
Ответ: ___________
16 Найдите значение выражения
(312 ) −3 ⋅ 329
.
3−11
Ответ: ___________
139
17 Найдите корень уравнения 2 x 2 + 4 x − 5 =− x . Если уравнение имеет более одного корня, то в
ответе укажите больший из них.
Ответ: ___________
18 Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого
столбца. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
−2
А)
<0
x −1
Б) log 3 x < 0
РЕШЕНИЯ
В) 4− x > 4
x
Г)
<0
( x − 1) 2
3) (1; + ∞ )
4) (0; 1)
1) ( −∞; 0 )
2) ( −∞; − 1)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
19
А
Б
В
Г
Найдите четырёхзначное число, большее 3300, но меньшее 4500, которое делится на 72 и сумма
цифр которого равна 9, при этом все цифры искомого числа различны. В ответе укажите какоенибудь одно такое число.
Ответ: ___________
20 Расстояние между пристанями А и В равно 88 км. Из А в В по течению реки отправился плот,
а через час вслед за ним отправился катер, которая, прибыв в пункт В, тотчас повернул обратно
и возвратился в А. К этому времени плот прошёл 31,5 км. Найдите скорость катера в стоячей
воде, если скорость течения реки равна 3 км/ч.
Ответ: ___________
21 Жук передвигается вдоль координатной прямой в любом направлении на единичный отрезок за
один ход. Сколько существует различных точек на координатной прямой, в которых жук может
оказаться, сделав ровно 8 ходов, стартуя из начала координат?
Ответ: ___________
!
140
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 7
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Стоимость проездного билета на три месяца составляет 3600 рублей, а стоимость билета на
одну поездку – 45 рублей. Таня купила проездной и сделала за три месяца 126 поездок. На
сколько рублей больше она бы потратила, если бы каждый раз покупала билет на одну поездку?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) масса электронной книги
Б) масса одной ягоды ежевики
В) масса автохолодильника
Г) масса взрослого бегемота
1) 12,5 г
2) 22 кг
3) 2,8 т
4) 200 г
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На графике показано изменение температуры вещества в зависимости от времени. На оси абсцисс откладывается время в минутах, прошедшее с начала охлаждения, на оси ординат –
температура вещества в градусах Цельсия.
t°C
400
300
200
100
0 1 2 3 4 5 t, мин
Определите по графику, на сколько градусов Цельсия охладилось тело за первые 3 минуты.
Ответ: ___________
4
U 2t
, где
R
U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах), найдите
Используя
формулу для вычисления работы постоянного тока (в джоулях) A =
A (в джоулях), если t = 17 c, U = 15 В и R = 18 Ом.
Ответ: ___________
141
5
В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность
того, что орёл выпадет ровно 1 раз.
Ответ: ___________
6
Союз потребителей определяет рейтинг соотношения «цена-качество» кофемашин. Рейтинг вычисляется на основе цены С, функциональности F , надежности N и простоты в использовании
P . Каждый отдельный показатель оценивается экспертами по пятибалльной шкале целыми
числами от 0 до 4. Итоговый рейтинг вычисляется по формуле
R =8 ⋅ (3F + 2 N + P) − 0, 02C .
В таблице приведены средняя цена и оценки каждого показателя для нескольких моделей кофемашин.
Модель
кофемашины
А
Б
В
Г
Цена
Функциональность
Надежность
Простота
3600
5200
4800
4700
2
4
3
3
1
3
4
2
4
0
3
2
Определите наивысший рейтинг представленных в таблице моделей кофемашин.
Ответ: ___________
7
На графике показана зависимость скорости автомобиля от времени. На оси абсцисс откладывается время в секундах. На оси ординат – скорость в м/с.
v, м/с
30
25
20
15
10
5
0
2 4 6 8 10 12 14 16 18 20
t, с
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику
движения на этом интервале.
ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ
А) ускорение было равно нулю
Б) ускорение было отрицательным
В) ускорение было наибольшим
Г) ускорение было положительным, а скорость
превышала 10 м/с
В таблице под каждой буквой укажите соответствующий
Ответ:
142
А
Б
В
Г
ИНТЕРВАЛЫ ВРЕМЕНИ
1) 0 – 4 с
2) 4 – 8 с
3) 16 – 20 с
4) 8 – 16 с
номер.
8
В классе учатся 25 человек. Те, кто поступают в технические вузы сдают ЕГЭ по физике или
по информатике: 13 человек сдают ЕГЭ по физике, а 15 человек – по информатике. Выберите
утверждения, которые следуют из приведённых данных.
1) В этом классе хотя бы 16 человек поступают в технические вузы;
2) найдутся хотя бы два человека, которые сдают оба экзамена;
3) если ученик не сдаёт ЕГЭ по физике, то он обязательно сдаёт ЕГЭ по информатике;
4) не найдётся 11 человек, которые не поступают в технические вузы.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
Найдите площадь трапеции, изображенной на
клетчатой бумаге с размером клетки 1 см 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ: ___________
1 см
м
10 Стену ванной комнаты, имеющую форму прямоугольника со сторонами 4 м и 7 м, требуется
выложить плиткой, имеющей форму прямоугольника со сторонами 10 см и 20 см. Сколько потребуется таких плиток?
Ответ: ___________
11
В бак, имеющий форму правильной четырёхугольной призмы со
стороной основания, равной 25 см, налита вода. В бак полностью
погрузили металлический кубик. Найдите сторону кубика, если уровень воды в баке поднялся на 12,8 см. Ответ выразите в сантиметрах.
h
Ответ: ___________
12 Около четырёхугольника PQRS описана окружность с центром O , через который проходят
диагонали PR и QS . Найдите угол PQS , если известно, что угол POQ равен 70°. Ответ
дайте в градусах.
Ответ: ___________
13 Даны два цилиндра. Радиус основания и высота первого равны
соответственно 20 и 9, а второго – 3 и 4. Во сколько раз площадь
боковой поверхности первого цилиндра больше площади боковой
поверхности второго?
Ответ: ___________
143
14 Найдите значение выражения 4 6 : 2 + 4 .
7 5 7
Ответ: ___________
15 В магазине электронной техники клавиатура стоит 1860 рублей. Сейчас магазин проводит акцию: при покупке двух клавиатур скидка на вторую клавиатуру 25%. Сколько рублей придётся
заплатить за покупку двух клавиатур в период действия акции?
Ответ: ___________
16 Найдите значение выражения 5 14 ⋅ 126 .
Ответ: ___________
17 Найдите корень уравнения 22 x−9 = 0,125 .
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
Неравенства
А) log0,1 x > 1
Решения
1) (0,1; + ∞)
Б) log0,1 x < 1
2) (0;10)
В) log0,1 x > −1
3) (0; 0,1)
Г) log0,1 x < −1
4) (10; + ∞)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите шестизначное натуральное число, которое записывается только цифрами 3 и 0 и делится
на 36. В ответе запишите одно их этих чисел.
Ответ: ___________
20 Из одной точки круговой трассы, длина которой равна 7 км, одновременно в одном направлении выехали два велосипедиста. Через 24 минуты после старта первый велосипедист впервые
обогнал второго на круг. Найдите скорость первого велосипедиста, если известно, что 7 кругов
он завершил на 50 минут раньше второго. Ответ дайте в км/ч.
Ответ: ___________
21 На экране компьютера хаотично двигаются красные, жёлтые и зелёные точки. При столкновении двух красных точек они превращаются в три жёлтые и одну зелёную. При столкновении
двух жёлтых они превращаются в одну красную и одну зелёную. В начальный момент времени
на экране были только красные точки. Через пять минут красных точек стало меньше, жёлтых
не появилось, зато появилось 30 зелёных. На сколько уменьшилось количество красных точек?
Ответ: ___________
!
144
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 8
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Стоимость проездного билета на полгода составляет 6000 рублей, а стоимость билета на одну
поездку – 50 рублей. Ваня купил проездной и сделал за полгода 220 поездок. На сколько
рублей больше он бы потратил, если бы каждый раз покупал билет на одну поездку?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) масса электронной клавиатуры
Б) масса спелого грецкого ореха
В) масса легкового автомобиля
Г) масса взрослого кита
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 15 г
2) 2500 кг
3) 700 г
4) 120 т
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На графике показано изменение температуры вещества в зависимости от времени. На оси абсцисс откладывается время в минутах, прошедшее с начала нагревания, на оси ординат – температура вещества в градусах Цельсия.
t°C
400
300
200
100
0 1 2 3 4 5 t, мин
Определите по графику, сколько минут температура вещества оставалась постоянной.
Ответ: ___________
4
U 2t
, где U –
R
напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах), найдите A
Используя формулу для вычисления работы постоянного тока (в джоулях) A =
(в джоулях), если t = 19 c, U = 12 В и R = 20 Ом.
Ответ: ___________
145
5
В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность
того, что орёл выпадет ровно 3 раза.
Ответ: ___________
6
Союз потребителей определяет рейтинг соотношения «цена-качество» стиральных машин. Рейтинг вычисляется на основе цены С, функциональности F , надежности N и простоты в
использовании P . Каждый отдельный показатель оценивается экспертами по пятибалльной
шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле
R =⋅
5 (3F + 4 N + 2 P) − 0, 001C .
В таблице приведены средняя цена и оценки каждого показателя для нескольких моделей стиральных машин.
Модель
стиральной машины
А
Б
В
Г
Цена
Функциональность
Надежность
Простота
16100
18200
20300
21500
2
2
3
4
0
1
1
1
4
3
1
0
Определите наивысший рейтинг представленных в таблице моделей стиральных машин.
Ответ: ___________
7
На графике показана зависимость скорости автомобиля от времени. На оси абсцисс откладывается время в секундах. На оси ординат – скорость в м/c.
v, м/с
30
25
20
15
10
5
0
2 4 6 8 10 12 14 16 18
t, с
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику
движения на этом интервале.
ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ
А) ускорение было равно нулю
Б) ускорение было отрицательным
В) ускорение было наибольшим
Г) ускорение было положительным, а скорость
превышала 20 м/с
ИНТЕРВАЛЫ ВРЕМЕНИ
1) 14 – 18 с
2) 0 – 4 с
3) 10 – 14 с
4) 4 – 10 с
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
146
А
Б
В
Г
8
Литературный кружок посещают 20 человек, из них 10 человек любят поэзию Пушкина,
а 14 человек – Лермонтова. Выберите утверждения, которые следуют из приведённых данных.
В этом классе:
1) если ученик любит поэзию Пушкина, то он обязательно не любит поэзию Лермонтова;
2) хотя бы 14 человек любят поэзию;
3) не найдётся 7 человек, которые не любят поэзию;
4) найдутся хотя бы 6 человек, которые любят поэзию обоих поэтов;
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
Найдите площадь трапеции, изображенной на
клетчатой бумаге с размером клетки 1 см 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ: ___________
1 см
м
10 Дно бассейна, имеющего форму прямоугольника со сторонами 26 м и 39 м, требуется выложить
плиткой, имеющей форму прямоугольника со сторонами 40 см и 60 см. Сколько потребуется
таких плиток?
Ответ: ___________
11
В бак, имеющий форму прямоугольного параллелепипеда со
сторонами основания 48 см и 40 см и высотой, равной 40 см,
налита вода до уровня h = 30 см. В бак полностью погрузили
металлический кубик со стороной 24 см. До какого уровня поднялась вода в баке? Ответ выразите в сантиметрах.
h
Ответ: ___________
12 Около четырёхугольника KLMN описана окружность с центром O , через который проходят
диагонали KM и LN . Найдите угол MKN , если известно, что угол LOM равен 80°. Ответ
дайте в градусах.
Ответ: ___________
13 Даны два цилиндра. Радиус основания и высота первого равны
соответственно 25 и 18, а высота второго – 5. Площадь боковой
поверхности первого цилиндра больше площади боковой поверхности второго в 2,5 раза. Найдите радиус основания второго цилиндра.
Ответ: ___________
147
14 Найдите значение выражения 31 4 : 5 + 2 .
5 9 7
Ответ: ___________
15 В книжном магазине любой путеводитель стоит 1250 рублей. Сейчас магазин проводит акцию:
при покупке двух путеводителей – скидка на второй путеводитель 30%. Сколько рублей придётся заплатить за покупку двух путеводителей в период действия акции?
Ответ: ___________
16 Найдите значение выражения 6 60 ⋅ 135 .
Ответ: ___________
1
17 Найдите корень уравнения 63− 2 x = .
6
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
Неравенства
А)
Б)
В)
Г)
log0,25 x > 1
log0,25 x < 1
log0,25 x > −1
log0,25 x < −1
Решения
1)
2)
3)
4)
(0; 4)
(4; + ∞)
(0; 0, 25)
(0, 25; + ∞)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите семизначное натуральное число, которое записывается только цифрами 1 и 0 и делится
на 24. В ответе запишите одно их этих чисел.
Ответ: ___________
20 Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Через 40 минут после старта первый автомобиль впервые
обогнал второго на круг. Найдите скорость второго автомобиля, если известно, что 9 кругов он
завершил на 30 минут позже первого. Ответ дайте в км/ч.
Ответ: ___________
21 На экране компьютера хаотично двигаются красные, жёлтые и зелёные точки. При столкновении трёх красных точек они превращаются в четыре жёлтые и одну зелёную. При столкновении
пяти жёлтых они превращаются в две красные и одну зелёную. В начальный момент времени на
экране были только красные точки. Через пять минут красных точек стало меньше, жёлтых не
появилось, зато появилось 36 зелёных. На сколько увеличилось количество всех точек на экране?
Ответ: ___________
!
148
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 9
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Стоимость проездного билета на год составляет 12000 рублей, а стоимость билета на одну поездку – 55 рублей. Соня купила проездной и сделала за год 410 поездок. На сколько рублей
больше она бы потратила, если бы каждый раз покупала билет на одну поездку?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) масса страусиного яйца
Б) масса воробья
В) масса взрослого жирафа
Г) масса стиральной машины
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 600 г
2) 750 кг
3) 30 г
4) 1,2 т
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На графике показано изменение температуры вещества в зависимости от времени. На оси абсцисс откладывается время в минутах, прошедшее с начала охлаждения, на оси ординат – температура вещества в градусах Цельсия.
t°C
50
40
30
20
10
4
8
12
16
20 t, мин
Определите по графику, до скольких градусов Цельсия вещество охладилось к тому моменту,
как его температура перестала меняться.
Ответ: ___________
4
U 2t
, где U –
R
напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах), найдите A (в джоулях), если t = 18 c, U = 9 В и R = 12 Ом.
Используя формулу для вычисления работы постоянного тока (в джоулях) A =
Ответ: ___________
149
5
В случайном эксперименте симметричную монету бросают три раза. Найдите вероятность того,
что орёл выпадет ровно 1 раз.
Ответ: ___________
6
Союз потребителей определяет рейтинг соотношения «цена-качество» кухонных комбайнов.
Рейтинг вычисляется на основе цены С, функциональности F , надежности N и простоты
в использовании P . Каждый отдельный показатель оценивается экспертами по пятибалльной
шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле
R =⋅
8 (2 F + 5 N + 3P) − 0, 01C .
В таблице приведены средняя цена и оценки каждого показателя для нескольких моделей кухонных комбайнов.
Модель
кухонного комбайна
А
Б
В
Г
Цена
Функциональность
Надежность
Простота
13200
13900
14500
18600
3
2
3
4
0
1
1
4
4
3
3
0
Определите наименьший рейтинг представленных в таблице моделей кухонных комбайнов.
Ответ: ___________
7
На графике показана зависимость скорости автомобиля от времени. На оси абсцисс откладывается время в секундах. На оси ординат – скорость в м/c.
v, м/с
30
25
20
15
10
5
0
2 4 6 8 10 12 14 16 18 20
t, с
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику
движения на этом интервале.
ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ
ИНТЕРВАЛЫ ВРЕМЕНИ
А) ускорение было равно нулю
Б) ускорение было положительным
В) ускорение было наименьшим
Г) ускорение было отрицательным, а скорость
превышала 25 м/с
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
150
А
Б
В
Г
1) 18 – 20 с
2) 14 – 18 с
3) 10 – 14 с
4) 0 – 10 с
8
В классе учатся 28 человек, из них 13 человек занимаются бегом, а 18 человек – плаванием.
Выберите утверждения, которые следуют из приведённых данных.
1) В этом классе найдутся хотя бы два человека, которые занимаются обоими видами спорта;
2) все ученики занимаются спортом;
3) не найдётся 12 человек, которые не занимаются спортом;
4) найдется хотя бы один человек, который не занимается спортом.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте
в квадратных сантиметрах.
Ответ: ___________
1 см
м
10 Пол кухни, имеющей форму прямоугольника со сторонами 3,5 м и 3 м, требуется выложить
плиткой, имеющей форму прямоугольника со сторонами 15 см и 25 см. Сколько потребуется
таких плиток?
Ответ: ___________
11 В бак, имеющий форму правильной четырёхугольной призмы, налита вода. В бак полностью погрузили металлический кубик со
стороной 30 см. Найдите сторону основания бака, если уровень
воды в нём поднялся на 4,8 см. Ответ выразите в сантиметрах.
h
Ответ: ___________
12 Около четырёхугольника ABCD описана окружность с центром O , через который проходят
диагонали AC и BD . Найдите угол ACB, если известно, что угол AOD равен 110°. Ответ дайте
в градусах.
Ответ: ___________
13 Даны два цилиндра. Радиус основания первого равен 15, а радиус
основания и высота второго равны 21 и 20 соответственно. Площадь боковой поверхности первого цилиндра больше площади
боковой поверхности второго в 1,5 раза. Найдите высоту первого
цилиндра.
Ответ: ___________
1 2 5
14 Найдите значение выражения 28 : + .
5 7 6
Ответ: ___________
151
15
В магазине электронной техники пара беспроводных наушников стоит 4200 рублей. Сейчас
магазин проводит акцию: при покупке двух пар наушников – скидка на вторую пару 35%.
Сколько рублей придётся заплатить за покупку двух пар наушников в период действия акции?
Ответ: ___________
16
Найдите значение выражения 2 525 ⋅ 756 .
Ответ: ___________
17 Найдите корень уравнения 53 x+ 4 = 0,04 .
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
Неравенства
А) log0,2 x > 2
Б) log0,2 x < 2
В) log0,2 x > −2
Г) log0,2 x < −2
Решения
1)
2)
3)
4)
(0,04; + ∞)
(25; + ∞)
(0; 0,04)
(0; 25)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите шестизначное натуральное число, которое записывается только цифрами 6 и 0 и делится
на 72. В ответе запишите одно их этих чисел.
Ответ: ___________
20 Из одной точки круговой трассы, длина которой равна 24 км, одновременно в одном направлении стартовали два автомобиля. Через 48 минут после старта первый автомобиль впервые
обогнал второго на круг. Найдите скорость первого автомобиля, если известно, что 6 кругов он
завершил на 48 минут раньше второго. Ответ дайте в км/ч.
Ответ: ___________
21 На экране компьютера хаотично двигаются красные, жёлтые и зелёные точки. При столкновении двух красных точек они превращаются в шесть жёлтых и три зелёных. При столкновении
пяти жёлтых они превращаются в одну красную и одну зелёную. В начальный момент времени
на экране были только красные точки. Через пять минут на экране появилось 25 зелёных и
одна жёлтая. На сколько уменьшилось количество красных точек?
Ответ: ___________
!
152
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 10
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
В доме, в котором живет Иван, 9 этажей и несколько подъездов. Первый этаж нежилой. На
каждом из остальных этажей находится по 4 квартиры. Иван живет в квартире № 173. В каком
подъезде живет Иван?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) длина тела кошки
Б) толщина листа бумаги
В) высота железнодорожного вагона
Г) высота небоскрёба
1) 0,2 мм
2) 3,5 м
3) 140 м
4) 62 см
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
В командном конкурсе по литературе команды получили следующие баллы по разным темам:
Команда
Поэзия
Русская проза
Зарубежная проза
«Пушкин»
31
27
15
«Лермонтов»
34
25
11
«Толстой»
23
35
10
«Тургенев»
24
36
12
Для каждой команды баллы по всем темам суммируются, победителем считается команда, набравшая в сумме наибольшее количество баллов. Какое место заняла команда «Толстой»?
Ответ: ___________
4
Используя формулу мощности постоянного тока P = I 2 R , где P – мощность (в ваттах), I – сила
тока (в амперах), R – сопротивление (в омах), найдите сопротивление R в омах, если мощность
составляет 126 ватт, а сила тока равна 6 амперам.
Ответ: ___________
5
Фабрика шьёт пальто. В среднем из 240 пальто 12 пальто имеют брак. Найдите вероятность
того, что случайно выбранное пальто окажется без брака.
Ответ: ___________
153
6
Магазин закупает товары по оптовым ценам, продает по розничным. В таблице показаны общие
суммы закупок и продаж за 5 месяцев.
Месяц
Сумма закупок, тыс. руб.
Сумма продаж, тыс. руб.
Январь
90
95
Февраль
70
105
Март
75
115
Апрель
95
105
Май
100
110
Пользуясь таблицей, поставьте в соответствие каждому из указанных месяцев характеристику
доходов и расходов в этом месяце.
МЕСЯЦЫ
А) январь
Б) февраль
В) март
Г) май
ХАРАКТЕРИСТИКИ
1) сумма закупок в этом месяце наибольшая в период с января по май
2) разница между суммами продаж и закупок в этом месяце наибольшая
3) сумма закупок в этом месяце меньше, чем сумма закупок в предыдущем
4) разница между суммами продаж и закупок в этом месяце наименьшая
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
7
А
Б
В
Г
На рисунке изображён график функции y = f ( x) ,
определённой на промежутке [ −5; 6] . Какие из утверждений относительно этой функции неверны?
Укажите их номера в порядке возрастания.
y
1) Функция убывает на промежутке [1; 6] .
1
2) f (0) = 3 .
0 1
x
3) Функция принимает положительные значения при
x ∈ (−4; 0) .
4) Наибольшее значение функции равно 4.
Ответ: ___________
8
В физико-математическом классе 7 девочек и 15 мальчиков. Учитель по литературе хочет на
уроке вызвать к доске 5 учеников. Выберите утверждения, которые будут верны при указанных
условиях независимо от того, кого учитель вызовет к доске.
1) Найдутся 9 мальчиков, которых не вызвали к доске.
2) Найдутся 3 девочки, которых вызвали к доске.
3) Если ученик мальчик, то его вызвали к доске.
4) Не найдётся 8 мальчиков, которых вызвали к доске.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
154
9
Найдите площадь четырехугольника, изображенного на
клетчатой бумаге с размером клетки 1 см (см. рис.). Ответ
дайте в квадратных сантиметрах.
Ответ: ___________
1 см
м
10 Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 17:00?
Ответ: ___________
11 Пирамида Снофру имеет форму правильной четырёхугольной
пирамиды, сторона основания которой равна 220 м, а высота – 104 м. Сторона основания точной музейной копии этой
пирамиды равна 88 см. Найдите высоту музейной копии. Ответ
дайте в сантиметрах.
Ответ: ___________
12 В выпуклом четырёхугольнике KLMN известно, что KL = LM, MN = NK, ∠L = 95° , ∠K = 80° .
Найдите угол N. Ответ дайте в градусах.
Ответ: ___________
13 Даны два шара с радиусами 15 и 3. Во сколько раз площадь
поверхности первого шара больше площади поверхности
второго?
Ответ: ___________
14 Найдите значение выражения
113 5 3
− : .
21 7 10
Ответ: ___________
15 Длины двух дорог относятся как 7:9, при этом одна из них длиннее другой на 40 км. Найдите
длину меньшей дороги. Ответ дайте в километрах.
Ответ: ___________
16 Найдите значение выражения 12sin120° ⋅ cos150° .
Ответ: ___________
155
17 Найдите корень уравнения
13 + 4 x − 5 =
0.
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЕ
А) 0, 2 x > 125
1) (3; + ∞)
Б) 0, 2 x < 125
2) (−∞; − 3)
В) 5 x < 125
3) (−∞; 3)
Г) 5 x > 125
4) (−3; + ∞)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите четырёхзначное число, которое в 5 раз меньше куба некоторого натурального числа.
В ответе укажите какое-нибудь одно такое число.
Ответ: ___________
20 Ане нужно решить 435 задач. Ежедневно она решает на одно и то же количество задач больше
по сравнению с предыдущим днем. Известно, что за первый день Аня решила 8 задач. Определите, сколько задач было решено за пятый день, если всё задание было выполнено за 15 дней.
Ответ: ___________
21 На столе в ряд лежат коробки с карандашами: красными, жёлтыми и зелёными. Слева от коробки
с красными карандашами находятся 15 карандашей, справа от коробки с жёлтыми карандашами
находятся 10 карандашей. Всего в коробках 18 карандашей. Сколько жёлтых карандашей?
Ответ: ___________
!
156
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 11
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
В доме, в котором живет Петр, 12 этажей и несколько подъездов. На каждом этаже, кроме
первого, находится по 4 квартиры, на первом – 2 квартиры. Пётр живет в квартире № 212.
В каком подъезде живет Петр?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) высота потолка в комнате
Б) высота Шуховской башни
В) высота гриба подберезовика
Г) длина реки Обь
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 12 см
2) 160 м
3) 2,7 м
4) 3650 км
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На командной олимпиаде по физике команды получили следующие баллы в разных турах:
Команда
Теоретический тур
Экспериментальный тур
Заключительный тур
«Ньютон»
31
27
24
«Лоренц»
24
32
28
«Кулон»
21
33
26
«Ампер»
34
24
27
Для каждой команды баллы по всем турам суммируются, победителем считается команда, набравшая в сумме наибольшее количество баллов. Какое место заняла команда «Лоренц»?
Ответ: ___________
4
Используя формулу центростремительного ускорения a = ω2 R , где a – центростремительное
ускорение (в м/c2), ω – угловая скорость (в с−1), а R – радиус окружности (в метрах), найдите
радиус окружности в метрах, если угловая скорость равна 5 с−1, а центростремительное ускорение равно 62,5 м/с2.
Ответ: ___________
5
Ателье шьёт пальто. В среднем из 360 пальто 90 пальто имеют брак. Найдите вероятность того,
что случайно выбранное пальто окажется без брака.
Ответ: ___________
157
6
Магазин закупает товары по оптовым ценам, продает по розничным. В таблице показаны общие
суммы закупок и продаж за 5 месяцев.
Декабрь
Сумма закупок
(тыс. руб.)
80
Сумма продаж
(тыс. руб.)
90
Январь
90
95
Февраль
95
105
Март
75
115
Апрель
85
110
Месяц
Пользуясь таблицей, поставьте в соответствие каждому из указанных месяцев характеристику
доходов и расходов в этом месяце.
МЕСЯЦЫ
ХАРАКТЕРИСТИКИ
А) январь
Б) февраль
В) март
Г) апрель
1) сумма закупок в этом месяце наибольшая в период с декабря по апрель
2) разница между суммами продаж и закупок в этом месяце наибольшая
3) сумма продаж в этом месяце меньше, чем сумма продаж в предыдущем
4) разница между суммами продаж и закупок в этом месяце наименьшая
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
7
А
Б
В
Г
На рисунке изображён график функции y = f ( x) , определённой на промежутке [ −5; 5] . Какие из утверждений относительно этой функции верны? Укажите их номера в порядке
возрастания.
y
1) Функция возрастает на промежутке [ −2; 2] .
0
2)
1
1
x
f (−4) > f (0) .
3) Функция принимает отрицательные значения при
x ∈ (−4; 0) (4; 5] .
4) Прямая y = 0 пересекает график функции в двух точках.
Ответ: ___________
8
В классе 28 учащихся. Из них 8 человек сдают ЕГЭ по физике. Из 28 учащихся 10 человек участвовало в олимпиаде по физике. Выберите утверждения, которые будут верны при указанных
условиях независимо от того, участвовали или нет в олимпиаде те, кто сдаёт ЕГЭ по физике.
1) Хотя бы один из тех, кто сдаёт ЕГЭ по физике, участвовал в олимпиаде.
2) Хотя бы один из тех, кто не сдаёт ЕГЭ по физике, участвовал в олимпиаде.
3) Если учащийся сдаёт ЕГЭ по физике, то он участвовал в олимпиаде.
4) Если учащийся участвовал в олимпиаде, то он сдаёт ЕГЭ по физике.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
158
9
Найдите площадь четырехугольника, изображенного на
клетчатой бумаге с размером клетки 1 см (см. рис.). Ответ
дайте в квадратных сантиметрах.
Ответ: ___________
1 см
м
10 Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 11:00 ?
Ответ: ___________
11 Пирамида Микерина имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 108 м, а
высота – 66 м. Сторона основания точной музейной копии
этой пирамиды равна 27 см. Найдите высоту музейной копии.
Ответ дайте в сантиметрах.
Ответ: ___________
12 В выпуклом четырёхугольнике PQRS известно, что PQ = QR, RS = SP, ∠S = 91° , ∠P = 92° .
Найдите угол Q. Ответ дайте в градусах.
Ответ: ___________
13 Даны два шара с радиусами 45 и 5. Во сколько раз площадь
поверхности первого шара больше площади поверхности
второго?
Ответ: ___________
14 Найдите значение выражения
166 13 3
− : .
15 5 7
Ответ: ___________
15 Длины двух дорог относятся как 5:24, при этом одна из них длиннее другой на 570 км. Найдите
длину большей дороги. Ответ дайте в километрах.
Ответ: ___________
16 Найдите значение выражения 20sin150° ⋅ cos120° .
Ответ: ___________
159
17 Найдите корень уравнения
15 − 3 x − 3 =.
0
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А) 0,1x > 100
1) (2; + ∞)
Б) 0,1x < 100
2) (−2; + ∞)
В) 10 x < 100
3) (−∞; 2)
Г) 10 x > 100
4) (−∞; − 2)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите пятизначное число, которое в 3 раза меньше четвертой степени некоторого натурального
числа. В ответе укажите какое-нибудь одно такое число.
Ответ: ___________
20 Рабочие асфальтируют дорогу длиной 1060 м. Ежедневно они асфальтируют на одно и то же
количество метров больше по сравнению с предыдущим днем. Известно, что за первый день
рабочие заасфальтировали 15 м дороги. Определите, сколько метров дороги было заасфальтировано за седьмой день, если вся работа была выполнена за 20 дней.
Ответ: ___________
21 В витрине магазина стоят в ряд корзины с фруктами: яблоками, грушами и бананами. Слева от
корзины с яблоками находятся 22 фрукта, справа от корзины с грушами – 26 фруктов. Всего в
корзинах 43 фрукта. Сколько груш находится в витрине?
Ответ: ___________
!
160
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 12
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
В доме, в котором живет Мария, 17 этажей и несколько подъездов. На каждом этаже, кроме
первого, находится по 4 квартиры, на первом – 3 квартиры. Мария живет в квартире № 517.
В каком подъезде живет Мария?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) диаметр швейной иглы
Б) высота письменного стола
В) длина автобусного маршрута
Г) высота горы Эверест
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 8 848 м
2) 0,7 мм
3) 70 см
4) 40 км
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
В конкурсе «Математический бой» команды получили следующие баллы за решение задач по
разным темам:
Команда
Геометрия
Алгебра
Теория вероятностей
«Архимед»
35
22
30
«Пифагор»
28
25
27
«Ферма»
21
24
28
«Декарт»
33
23
29
Для каждой команды баллы по всем темам суммируются, победителем считается команда, набравшая в сумме наибольшее количество баллов. Какое место заняла команда «Пифагор»?
Ответ: ___________
4
Используя формулу, описывающую закон Джоуля-Ленца Q = I 2 Rt , где Q – количество теплоты
(в джоулях), I – сила тока (в амперах), R – сопротивление цепи (в омах), а t – время (в секундах), найдите время t в секундах, если Q = 1592,5 Дж, I = 7A, R = 5 Ом.
Ответ: ___________
5
Из 40 вопросов, содержащихся в списке вопросов к экзамену, студент не выучил 7. На экзамене
он случайным образом получает вопрос из списка всех вопросов. Найдите вероятность того,
что ему попадётся выученный вопрос.
Ответ: ___________
161
6
Магазин закупает товары по оптовым ценам, продает по розничным. В таблице показаны общие
суммы закупок и продаж за 5 месяцев.
Месяц
Сумма закупок
( тыс. руб.)
Сумма продаж
(тыс. руб.)
Ноябрь
90
125
Декабрь
95
105
Январь
100
105
Февраль
105
115
Март
85
125
Пользуясь таблицей, поставьте в соответствие каждому из указанных месяцев характеристику
доходов и расходов в этом месяце.
МЕСЯЦЫ
А) декабрь
Б) январь
В) февраль
Г) март
ХАРАКТЕРИСТИКИ
1) сумма закупок в этом месяце наибольшая в период с ноября по март
2) разница между суммами продаж и закупок в этом месяце наибольшая
3) сумма продаж в этом месяце меньше, чем сумма продаж в предыдущем
4) разница между суммами продаж и закупок в этом месяце наименьшая
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
7
А
Б
В
Г
На рисунке изображён график функции y = f ( x) , определённой на промежутке [ −5; 5] . Какие из утверждений относительно этой функции неверны? Укажите их номера в
порядке возрастания.
1) Функция возрастает на промежутке [ −5; 0] .
2)
y
1
0 1
x
f (−2) =
0.
3) f (−4) > f (2) .
4) Наименьшее значение функции равно −4 .
Ответ: ___________
8
В автосалоне для продажи выставлено 40 автомобилей, из них 15 с механической коробкой
передач, остальные – с автоматической. В 8 из этих 40 автомобилей салон собирается установить сигнализацию. Выберите утверждения, которые будут верны при указанных условиях
независимо от того, в какие автомобили салон установит сигнализацию.
1) Найдётся 16 автомобилей с автоматической коробкой передач без сигнализации.
2) Найдётся 6 автомобилей с механической коробкой передач, но без сигнализации.
3) Если автомобиль с сигнализацией, то он с автоматической коробкой передач.
4) Если автомобиль без сигнализации, то он с механической коробкой передач
162
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см (см. рис.). Ответ дайте
в квадратных сантиметрах.
Ответ: ___________
1 см
м
10 Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 14:00?
Ответ: ___________
11 Пирамида Сахуре имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 78 м, а высота – 48 м.
Сторона основания точной музейной копии этой пирамиды равна
26 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
Ответ: ___________
12 В выпуклом четырёхугольнике ABCD известно, что AB = BC, AD = CD, ∠B = 62° , ∠D = 166° .
Найдите угол A. Ответ дайте в градусах.
Ответ: ___________
13 Даны два шара с радиусами 32 и 4. Во сколько раз площадь
поверхности первого шара больше площади поверхности
второго?
Ответ: ___________
14 Найдите значение выражения
7 17 3
+ : .
6 2 4
Ответ: ___________
15 Длины двух дорог относятся как 1:5, при этом одна из них длиннее другой на 190 км. Найдите
длину меньшей дороги. Ответ дайте в километрах.
Ответ: ___________
163
16 Найдите значение выражения 14sin135° ⋅ cos315° .
Ответ: ___________
17 Найдите корень уравнения
20 + 4 x − 4 =.
0
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А) 0,5 x > 16
1) (−4; + ∞)
Б) 0,5 x < 16
2) (−∞; − 4)
В) 2 x < 16
Г) 2 x > 16
3) (4; + ∞)
4) (−∞; 4)
В таблице под каждой буквой укажите номер её возможного значения.
Ответ:
А
Б
В
Г
19 Найдите четырёхзначное число, которое в 7 раз меньше куба некоторого натурального числа.
В ответе укажите какое-нибудь одно такое число.
Ответ: ___________
20 Машинистка печатает рукопись, состоящую из 884 страниц. Ежедневно она печатает на одно и
то же количество страниц больше по сравнению с предыдущим днем. Известно, что за первый
день машинистка напечатала 12 страниц. Определите, сколько страниц было напечатано за
шестой день, если вся работа была выполнена за 17 дней.
Ответ: ___________
21 На столе в ряд лежат стопки тетрадей: по алгебре, геометрии и теории вероятностей. Слева
от тетрадей по алгебре находятся 19 тетрадей, справа от тетрадей по геометрии находятся
10 тетрадей. Всего на столе 24 тетради. Сколько тетрадей по теории вероятностей?
Ответ: ___________
!
164
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 13
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Каждый день кафе «Сладкоежка» расходует 19 кг сахара, который закупает пакетами по
900 граммов. Сколько пакетов сахара должно закупить кафе, чтобы его хватило на неделю?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) длительность варки яйца вкрутую
Б) время поездки на велосипеде на 50 км
В) время оборота луны вокруг земли
ЗНАЧЕНИЯ
1) 27 суток
2) 10 минут
3) 2 часа
4) 0,2 секунды
Г) продолжительность разряда молнии
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике приведена зависимость напряжения в электрической сети фонарика
от времени. На горизонтальной оси отмечено время работы фонарика (в часах), на вертикальной
оси – напряжение (в вольтах).
U, в
1,6
1,2
0,8
0,4
0
5
10
15
20
t, час
Определите по рисунку, за сколько часов напряжение упадёт с 1,2 до 0,8 В.
Ответ: ___________
4
q2
,
2C
где C – ёмкость конденсатора (в Ф), а q – заряд на одной обкладке конденсатора (в Кл), найдите
Используя формулу для вычисления энергии заряженного конденсатора (в джоулях) W =
q (в Кл), если C= 5 ⋅ 10−4 Ф и W = 0,049 Дж.
Ответ: ___________
165
5
Случайным образом выбрано трёхзначное число. Найдите вероятность того, что оно делится на 4.
Ответ: ___________
6
В таблице даны результаты ЕГЭ девяти абитуриентов.
Номер
абитуриента
1
Балл по русскому
языку
70
Балл по
географии
70
Балл по
экономике
60
2
58
75
70
3
66
68
80
4
64
72
76
5
72
62
78
6
62
68
75
7
80
60
64
8
60
72
82
9
60
70
74
При поступлении в вуз суммируются балл по русскому языку и лучший из баллов по географии
и экономике. Для поступления нужно набрать не менее 140 баллов. В ответе укажите без пробелов, запятых и других дополнительных символов номера абитуриентов, набравших меньше
65 баллов по географии и поступивших в вуз.
Ответ: ___________
7
На рисунке изображён график функции f ( x) . Пользуясь графиком, поставьте в соответствие
каждому из указанных интервалов характеристику функции или её производной.
y
y = f(x)
1
–2
ИНТЕРВАЛЫ
А) (−2;1)
Б) (4; 7)
В) (−1; 5)
Г) (5;12)
166
0
1
12 x
ХАРАКТЕРИСТИКИ
1) функция отрицательна на всём интервале
2) производная функции неотрицательна на всём интервале
3) функция положительна на всём интервале
4) производная функции неположительна на всём интервале
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
Петя решил задач больше, чем Маша, и больше, чем Таня. Ваня решил задач меньше, чем Петя,
и меньше, чем Маша. Выберите утверждения, которые верны при указанных условиях.
1) Петя решил больше всех задач.
2) Ваня решил меньше всех задач.
3) Таня решила меньше всех задач.
4) Таня решила задач меньше, чем Маша.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
Найдите площадь ромба, изображенного на клетчатой бумаге
с размером клетки 1 см
1 см (см. рис.). Ответ дайте в
квадратных сантиметрах.
Ответ: ___________
1м
10 Школьник ростом 1,6 м, стоящий на расстоянии 4 м от фонаря, отбрасывает тень длиной 1 м.
Сколько метров составляет высота фонаря?
Ответ: ___________
11 Открытую коробку, имеющую форму куба с ребром 60 см, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую
необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Ответ: ___________
12 В параллелограмме диагонали являются биссектрисами его углов и равны 24 и 10. Найдите
периметр параллелограмма.
Ответ: ___________
167
13 Даны два конуса. Радиус основания и высота первого конуса равны соответственно 8 и 3, а второго – 2 и 6. Во сколько раз объём
первого конуса больше объёма второго?
Ответ: ___________
14 Найдите значение выражения
4,8
.
5,7 − 5,1
Ответ: ___________
15 В период распродажи магазин снижал цены дважды: в первый раз на 10%, во второй – на 15%.
Сколько рублей стал стоить фен после второго снижения цен, если до начала распродажи он
стоил 2000 рублей?
Ответ: ___________
16 Найдите значение выражения log 1 27 .
9
Ответ: ___________
17 Найдите корень уравнения (2 x − 1)3 =.
64
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А) ( x − 1)( x − 2) 2 ≤ 0
( x − 2) 2
Б)
≤0
x −1
x −1
В)
≤0
( x − 2) 2
Г) ( x − 1) 2 ( x − 2) ≤ 0
РЕШЕНИЯ
1) (−∞;1) {2}
2) (−∞;1]
3) (−∞;1] {2}
4) (−∞; 2]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите трёхзначное число, сумма цифр которого равна 21, а сумма квадратов цифр делится
на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
Ответ: ___________
168
20
Две трубы, работая одновременно, наполняют бассейн за 12 часов. Первая труба наполняет
бассейн на 10 часов быстрее второй. За сколько часов наполняет бассейн вторая труба?
Ответ: ___________
21 Две бригады уложили асфальт на участке дороги длиной 51 метр и покрасили забор, начав и закончив одновременно. Сначала первая бригада красила забор, а вторая укладывала асфальт, но в
какой-то момент они поменялись. Вторая бригада обе работы выполняет в 4 раза быстрее первой.
Сколько метров дороги заасфальтировала первая бригада, если она покрасила половину забора?
Ответ: ___________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
169
ВАРИАНТ № 14
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Каждый день кондитерский магазин продаёт 29 кг конфет «Белочка», которые закупает коробками по 6 кг. Сколько коробок конфет должен закупить магазин, чтобы их хватило на неделю?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) длительность драматического спектакля
Б) продолжительность полярной ночи в Мурманске
В) продолжительность вдоха в состоянии покоя
1) 174 суток
2) 7 минут
3) 2 часа
4) 2 секунды
Г) время варки макарон
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике приведена зависимость напряжения в электрической сети фонарика
от времени. На горизонтальной оси отмечено время работы фонарика (в часах), на вертикальной
оси – напряжение (в вольтах).
U, в
1,6
1,2
0,8
0,4
0
5
10
15
20
t, час
Определите по рисунку, на сколько вольт упадёт напряжение за 10 часов работы фонарика.
Ответ: ___________
4
q2
,
2C
где C – ёмкость конденсатора (в Ф), а q – заряд на одной обкладке конденсатора (в Кл), най-
Используя формулу для вычисления энергии заряженного конденсатора (в джоулях) W =
дите W (в Дж), если q = 0,009 Кл и C = 3 ⋅ 10−4 Ф.
Ответ: ___________
170
5
Случайным образом выбрано трёхзначное число. Найдите вероятность того, что оно делится
на 10.
Ответ: ___________
6
В таблице даны результаты ЕГЭ девяти абитуриентов.
Номер
абитуриента
Балл по русскому
языку
Балл по истории
Балл
по обществознанию
1
70
70
60
2
58
75
70
3
66
68
80
4
64
72
76
5
72
62
78
6
62
68
75
7
80
60
64
8
60
72
82
9
60
70
74
При поступлении в вуз суммируются балл по русскому языку и лучший из баллов по истории
и по обществознанию. Для поступления нужно набрать не менее 140 баллов. В ответе укажите
без пробелов, запятых и других дополнительных символов номера абитуриентов, набравших
меньше 65 баллов по русскому языку и поступивших в вуз.
Ответ: ___________
7
На рисунке изображён график функции f ( x) .
y
y = f(x)
1
–2
0
1
11
x
Пользуясь графиком функции, поставьте в соответствие каждому из указанных интервалов характеристику функции или её производной.
ИНТЕРВАЛЫ
А) ( −1; 3)
Б) (3; 7)
В) (−2; 2)
Г) (7; 9)
ХАРАКТЕРИСТИКИ
1) функция отрицательна на всём интервале
2) производная функции положительна на всём интервале
3) функция положительна на всём интервале
4) производная функции отрицательна на всём интервале
171
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
Петя пробежал дистанцию 500 м быстрее Маши, но медленнее Вани. Маша пробежала медленнее Тани, Ваня пробежал быстрее Тани. Выберите утверждения, которые верны при указанных
условиях.
1) Петя пробежал быстрее Тани.
2) Маша пробежала медленнее всех.
3) Ваня пробежал быстрее всех.
4) Таня пробежала быстрее Пети.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
Найдите площадь ромба, изображенного на клетчатой бумаге
с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ: ___________
1 см
м
10 Человек, стоящий на расстоянии 3,2 м от фонаря, отбрасывает тень длиной 80 см. Найдите рост
человека, если высота фонаря равна 8,5 м. Ответ выразите в метрах.
Ответ: ___________
11 Открытую коробку, имеющую форму куба с ребром 80 см, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую
необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Ответ: ___________
12 В параллелограмме диагонали являются биссектрисами его углов и равны 16 и 30. Найдите
периметр параллелограмма.
Ответ: ___________
13 Даны два конуса. Радиус основания и высота первого конуса равны соответственно 6 и 1, а второго – 2 и 3. Во сколько раз объём первого конуса
больше объёма второго?
Ответ: ___________
172
14 Найдите значение выражения
6, 4
.
3,7 − 3, 2
Ответ: ___________
15 В период распродажи магазин снижал цены дважды: в первый раз на 15%, во второй – на 20%.
Сколько рублей стал стоить телевизор после второго снижения цен, если до начала распродажи
он стоил 8000 рублей?
Ответ: ___________
16 Найдите значение выражения log 1 4 .
32
Ответ: ___________
17 Найдите корень уравнения (3 x − 1)3 =
0,125 .
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
2
А) ( x − 1)( x − 2) ≥ 0
( x − 2) 2
≥0
x −1
x −1
В)
≥0
( x − 2) 2
Б)
2
РЕШЕНИЯ
1) [1; 2) (2; + ∞)
2) [2; + ∞) {1}
3) (1; + ∞)
4) [1; + ∞)
Г) ( x − 1) ( x − 2) ≥ 0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите трёхзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится
на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
Ответ: ___________
20 Бассейн может наполняться через три трубы. Если будут открыты первая и вторая трубы, бассейн
наполнится за 9 часов. Если открыты вторая и третья – за 12 часов, а если открыты первая и
третья – за 18 часов. За сколько часов наполнится бассейн, если будут отрыты все три трубы?
Ответ: ___________
173
21 Две бригады уложили асфальт на участке дороги длиной 52 метра и покрасили 30 метров забора, начав и закончив одновременно. Сначала первая бригада красила забор, а вторая укладывала асфальт, но в какой-то момент они поменялись. Вторая бригада обе работы выполняет
в пять раз быстрее первой. Сколько метров дороги заасфальтировала вторая бригада, если она
покрасила 15 метров забора?
Ответ: ___________
!
174
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 15
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Каждый день кофейня расходует 9 литров молока, которое закупает пакетами по 2,2 литра.
Сколько пакетов молока должно закупить кафе, чтобы его хватило на неделю?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) время полной зарядки телефона
Б) время стоянки автобуса
В) время оборота луны вокруг своей оси
Г) рекорд мира в беге на 100 метров на стадионе
ЗНАЧЕНИЯ
1) 9,58 секунды
2) 1 минута
3) 3 часа
4) 27 суток
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике приведена зависимость напряжения в электрической сети фонарика
от времени. На горизонтальной оси отмечено время работы фонарика (в часах), на вертикальной
оси – напряжение (в вольтах).
U, в
1,6
1,2
0,8
0,4
0
5
10
15
20
t, час
Определите по рисунку, за сколько часов напряжение упадёт с 1,6 до 0,6 В.
Ответ: ___________
4
q2
,
2C
где C – ёмкость конденсатора (в Ф), а q – заряд на одной обкладке конденсатора (в Кл),
Используя формулу для вычисления энергии заряженного конденсатора (в джоулях) W =
найдите C (в Ф), если q = 0,006 Кл и W = 0,045 Дж.
Ответ: ___________
175
5
Случайным образом выбрано трёхзначное число. Найдите вероятность того, что оно делится на 5.
Ответ: ___________
6
В таблице даны результаты ЕГЭ девяти абитуриентов.
Номер
абитуриента
Балл по русскому
языку
Балл по биологии
Балл по химии
1
70
70
60
2
58
75
70
3
66
68
80
4
64
72
76
5
72
62
78
6
62
68
75
7
80
60
64
8
60
72
82
9
60
70
74
При поступлении в вуз суммируются балл по русскому языку и лучший из баллов по биологии
и химии. Для поступления нужно набрать не менее 140 баллов. В ответе укажите без пробелов, запятых и других дополнительных символов номера абитуриентов, набравших меньше
65 баллов по химии и поступивших в вуз.
Ответ: ___________
7
На рисунке изображён график функции f ( x) . Пользуясь графиком, поставьте в соответствие
каждому из указанных интервалов характеристику функции или её производной.
y
y = f(x)
1
–6
ИНТЕРВАЛЫ
А) (−3;1)
Б) (−6; − 2)
В) (−2; 2)
Г) (1; 2)
176
–4
–2
0
2
4
x
ХАРАКТЕРИСТИКИ
1) функция отрицательна на всём интервале
2) производная функции положительна на всём интервале
3) функция положительна на всём интервале
4) производная функции отрицательна на всём интервале
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
У Вани пятёрок за полугодие больше, чем у Пети, но меньше, чем у Маши. У Маши пятёрок
больше, чем у Тани, у Пети пятёрок меньше, чем у Тани. Выберите утверждения, которые
верны при указанных условиях.
1)
2)
3)
4)
У
У
У
У
Пети пятёрок меньше, чем у Маши.
Вани больше всего пятёрок.
двух учеников одинаковое количество пятёрок.
Пети меньше всего пятёрок.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
Найдите площадь ромба, изображенного на клетчатой бумаге
1 см (см. рис.). Ответ дайте в
с размером клетки 1 см
квадратных сантиметрах.
Ответ: ___________
1 см
м
10 Мужчина ростом 180 см стоит на расстоянии 6 м от фонаря высотой 9 м. Найдите длину его
тени. Ответ выразите в метрах.
Ответ: ___________
11 Открытую коробку, имеющую форму куба с ребром 50 см, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую
необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Ответ: ___________
12 В параллелограмме диагонали являются биссектрисами его углов и равны 48 и 14. Найдите
периметр параллелограмма.
Ответ: ___________
13 Даны два конуса. Радиус основания и высота первого конуса равны соответственно 10 и 3, а второго –
4 и 5. Во сколько раз объём первого конуса больше
объёма второго?
Ответ: ___________
177
14 Найдите значение выражения
8,5
.
6,8 − 6,3
Ответ: ___________
15
В период распродажи магазин снижал цены дважды: в первый раз на 20%, во второй – на
25%. Сколько рублей стал стоить холодильник после второго снижения цен, если до начала
распродажи он стоил 28000 рублей?
Ответ: ___________
16 Найдите значение выражения log
1 125 .
625
Ответ: ___________
17 Найдите корень уравнения (2 x − 3)3 =
0,008 .
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А) ( x − 2)( x − 3) 2 ≤ 0
РЕШЕНИЯ
1) (−∞; 2]
2
( x − 2)
≤0
x−3
x−2
В)
≤0
( x − 3) 2
Б)
Г) ( x − 2) 2 ( x − 3) ≤ 0
2) (−∞; 2] {3}
3) (−∞; 3]
4) (−∞; 3)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите трёхзначное число, сумма цифр которого равна 21, а сумма квадратов цифр делится
на 5. В ответе укажите какое-нибудь одно такое число.
Ответ: ___________
20
Бак объемом 300 литров может наполняться через две трубы. Из первой трубы за 7 минут
вытекает воды на 1,75 литра больше, чем из второй, а весь бак наполняется второй трубой
на 1 час медленнее, чем первой. Сколько литров воды вытекает за час из второй трубы?
Ответ: ___________
178
21 Две бригады уложили асфальт на участке дороги длиной 1 км и покрасили забор длиной 20 м,
начав и закончив одновременно. Сначала вторая бригада красила забор, а первая укладывала
асфальт, но в какой-то момент они поменялись. Первая бригада обе работы выполняет в 2 раза
быстрее первой. Сколько километров дороги заасфальтировала первая бригада, если она покрасила 10 м забора?
Ответ: ___________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
179
ВАРИАНТ № 16
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Антон платит за мобильную связь 200 рублей в месяц. В следующем году оператор собирается
повысить стоимость мобильной связи на 15%. Сколько рублей должен будет платить Антон за
мобильную связь ежемесячно в следующем году?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) рост ребёнка
Б) длина реки Лена
В) толщина волоса
Г) высота горы Эверест
1)
2)
3)
4)
8849 м
4294 км
0,1 мм
1,2 м
В таблице, под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
Б
В
Г
На рисунке показаны результаты измерения атмосферного давления в течение первых трех
дней марта. По горизонтали указаны дни измерений, по вертикали – значения атмосферного
давления в мм. рт. ст..
Атмосферное давление, мм рт. ст.
3
А
762
760
758
756
754
752
750
1 марта 2 марта
3 марта
Определите по графику наименьшее значение атмосферного давления 2 марта. Ответ дайте в
мм рт. ст.
Ответ: __________
180
4
Среднее арифметическое S трёх чисел a, b и с можно вычислить по формуле S =
Найдите среднее арифметическое чисел 2, 5 и 8.
a+b+c
.
3
Ответ: __________
5
Какова вероятность того, что случайное двузначное натуральное число делится на 5?
Ответ: __________
6
В бизнес-центре требуется установить 7 окон. В таблице приведена информация о стоимости
услуг трёх фирм, занимающихся установкой окон. Сколько нужно заплатить за самый дешёвый
вариант установки? Ответ дайте в рублях.
Фирма
Стоимость окна
(руб. за шт.)
Стоимость установки
окна (руб. за шт.)
Доставка
(руб.)
А
6200
2900
1000
Б
6400
2600
1100
В
6600
2500
1000
Ответ: __________
7
На графике изображена зависимость скорости движения тела от времени. На вертикальной оси
отмечена скорость движения тела в м/c, на горизонтальной – время в секундах, прошедшее от
начала движения.
v, м/с
80
60
40
20
0
15
30
45
60
75
90
105 120 135 150
t, с
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику
движения тела на этом интервале.
ИНТЕРВАЛЫ ВРЕМЕНИ
ХАРАКТЕРИСТИКИ
А) 0–30 секунд
1) скорость тела была не менее 20 м/с
Б) 60–90 секунд
В) 90–120 секунд
2) б
олее половины времени интервала тело двигалось с постоянной скоростью
3) половину времени интервала тело находилось в покое
Г) 120–150 секунд
4) скорость тела впервые достигла наибольшего значения
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
181
8
Двадцать пять выпускников инженерного класса сдавали ЕГЭ по физике. Самый низкий балл
в этом классе была равен 27, а самый высокий – 92. Выберите утверждения, которые верны
при указанных условиях.
1) Среди выпускников класса есть человек, который получил 92 балла за ЕГЭ по физике.
2) Среди выпускников класса есть человек, который получил 100 баллов за ЕГЭ по физике.
3) Найдутся два ученика в классе с одинаковыми баллами за ЕГЭ по физике.
4) Среди выпускников класса есть человек, который получил 27 баллов за ЕГЭ по физике.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
9
Найдите площадь ромба, изображенного на рисунке. Размер одной клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
Ответ: __________
1 см
м
10 Найдите величину вписанного угла, опирающегося на дугу, длина которой
11
составляет
длины окружности. Ответ дайте в градусах.
36
Ответ: __________
11 Даны два цилиндра. Первый цилиндр в два раза ниже второго, а
второй вдвое шире первого. Во сколько раз объём первого цилиндра меньше объёма второго?
Ответ: __________
12
В равнобедренном треугольнике ABC,
CH = 2 и sin A =
C
AC = BC , высота
2
. Найдите СВ.
2
Ответ: __________
A
182
H
B
13
Стороны основания правильной треугольной пирамиды равны 10, а
боковые рёбра равны 13. Найдите площадь боковой поверхности этой
пирамиды.
Ответ: __________
14 Найдите значение выражения
9 28 4
⋅ : .
4 3 5
Ответ: __________
15 Владельцы скидочной карты продуктового магазина получают скидку 5%. Сколько рублей заплатит владелец скидочной карты за покупку стоимостью 703 рубля?
Ответ: __________
16
Найдите значение выражения
1419
.
219 ⋅ 718
Ответ: __________
17 Найдите корень уравнения log 6 (8 − =
x ) log 6 (3 − x ) + 1 .
Ответ: __________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А) 5x ≥ 5
x
1
Б) ≥ 5
5
x
1
В) ≤ 5
5
Г) 5x ≤ 5
РЕШЕНИЯ
1) ( −∞; −1]
2) [ −1; +∞ )
3) [1;+∞ )
4) ( −∞;1]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите четырёхзначное натуральное число, кратное 19, такое что сумма его цифр на 1 больше
их произведения. В ответе укажите какое-нибудь одно такое число.
Ответ: __________
183
20 Первый рабочий изготовил 289 деталей за некоторое время. Второй рабочий изготовил 150 таких
же деталей и потратил на это на 2 часа меньше времени. Известно, что за один час, второй
рабочий делает на 7 деталей меньше, чем первый, а каждый из них делает меньше 20 деталей
за час. Сколько деталей в час делает первый рабочий?
Ответ: __________
21 В шахматном турнире принимали участие 15 шахматистов, причём каждый из них сыграл только
одну партию с каждым другим шахматистом. Сколько всего партий было сыграно в турнире?
Ответ: __________
!
184
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 17
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Андрей платит за мобильную связь 250 рублей в месяц. В следующем году оператор собирается
увеличить стоимость мобильной связи на 20%. Сколько рублей должен будет платить Андрей
за мобильную связь ежемесячно в следующем году?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) рост человека
1) 3530 км
Б) длина реки Волга
В) толщина лезвия бритвы
Г) высота горы Казбек
2) 1,8 м
3) 0,1 мм
4) 5054 м
В таблице, под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
Б
В
Г
На рисунке показаны результаты измерения атмосферного давления в течение первых трёх дней
мая. По горизонтали указаны дни измерений, по вертикали – значения атмосферного давления
в мм рт. ст.
Атмосферное давление, мм рт. ст.
3
А
762
760
758
756
754
752
750
1 мая
2 мая
3 мая
Определите по графику наибольшее значение атмосферного давления 3 мая. Ответ дайте в мм
рт.ст.
Ответ: __________
185
4
Среднее арифметическое S трёх чисел a, b и с можно вычислить по формуле S =
Найдите среднее арифметическое чисел 5, 6 и 10.
a+b+c
.
3
Ответ: __________
5
Какова вероятность того, что случайное двузначное натуральное число делится на три? Ответ
округлите до десятых.
Ответ: __________
6
В бизнес-центре требуется установить 5 окон. В таблице приведена информация о стоимости
услуг трёх фирм, занимающихся установкой окон. Сколько нужно заплатить за самый дешевый
вариант установки? Ответ дайте в рублях.
Фирма
Стоимость окна
(руб. за шт.)
Стоимость установки
окна (руб. за шт.)
Доставка
(руб.)
А
7600
3000
2000
Б
7800
2800
2100
В
7900
2600
Бесплатно
Ответ: __________
7
На графике изображена зависимость скорости движения тела от времени. На вертикальной оси
отмечена скорость движения тела в м/c, на горизонтальной – время в секундах, прошедшее от
начала движения. Пользуясь графиком, поставьте в соответствие каждому интервалу времени
характеристику движения тела на этом интервале.
v, м/с
8
6
4
2
0
4
2
ИНТЕРВАЛЫ ВРЕМЕНИ
6
8
10
12
14
16
18
20
1) тело остановилось второй раз после начала движения
2) скорость тела была не меньше 2 м/c на всём интервале
3) тело двигалось с постоянной скоростью 5 м/c в течение
1 секунды
4) тело находилось 2 секунды
В таблице под каждой буквой укажите соответствующий номер.
186
А
Б
t, с
ХАРАКТЕРИСТИКИ
А) 4–8 секунд
Б) 8–12 секунд
В) 12–16 секунд
Г) 18–22 секунд
Ответ:
22
В
Г
8
Двадцать выпускников класса сдавали ЕГЭ по математике. Самый низкий балл в этом классе
был равен 40, а самый высокий – 93. Выберите утверждения, которые верны при указанных
условиях.
1) Среди выпускников класса есть человек, который получил 93 балла за ЕГЭ по математике.
2) Среди выпускников класса есть человек, который получил 90 баллов за ЕГЭ по математике.
3) Среди выпускников класса есть человек, который получил 40 баллов за ЕГЭ по математике.
4) Найдутся два ученика в классе с одинаковыми баллами за ЕГЭ по математике.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других
дополнительных символов.
Ответ: __________
9
Найдите площадь ромба, изображенного на рисунке. Размер одной клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
Ответ: __________
1 см
м
10 Найдите величину вписанного угла, опирающегося на дугу, длина которой составляет
1
длины окружности. Ответ дайте в градусах.
9
Ответ: __________
11 Даны два цилиндра. Первый цилиндр в полтора раза ниже второго, а второй вдвое шире первого. Во сколько раз объём первого цилиндра меньше объёма второго?
Ответ: __________
12 В равнобедренном треугольнике ABC, AC = BC , высота CH = 3
и sin A =
C
1
. Найдите СВ.
2
Ответ: __________
A
H
B
187
13
Стороны основания правильной треугольной пирамиды равны 6,
а боковые рёбра равны 5. Найдите площадь боковой поверхности этой
пирамиды.
Ответ: __________
14 Найдите значение выражения
13 13 10
: + .
90 9 4
Ответ: __________
15
Владельцы скидочной карты канцелярского магазина получают скидку 10%. Учебник стоит
570 рублей. Сколько рублей заплатит владелец скидочной карты за этот учебник?
Ответ: __________
16
Найдите значение выражения
2212
.
213 ⋅ 1111
Ответ: __________
17
Найдите корень уравнения log 3 (3 + x=
) log 3 (1 − x ) + 2 .
Ответ: __________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом
столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А) 7 x ≥ 7
x
1
Б) ≥ 7
7
x
1
В) ≤ 7
7
Г) 7 x ≤ 7
РЕШЕНИЯ
1) ( −∞; − 1]
2) [ −1; + ∞ )
3) [1; + ∞ )
4) ( −∞;1]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите четырёхзначное натуральное число, кратное 11, такое что сумма его цифр на 1 меньше
их произведения. В ответе укажите какое-нибудь одно такое число.
Ответ: __________
188
20 Первый рабочий изготовил 120 деталей за некоторое время. Второй рабочий изготовил 130 таких
же деталей и потратил на это на 2 часа меньше времени. Известно, что за один час, второй
рабочий делает на 3 детали больше, чем первый. Сколько деталей в час делает первый рабочий?
Ответ: __________
21 В шахматном турнире принимали участие 13 шахматистов, причем каждый из них сыграл только
одну партию с каждым другим шахматистом. Сколько всего партий было сыграно в турнире?
Ответ: __________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
189
ВАРИАНТ № 18
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Найдите, на каком этаже находится квартира Алексея, если известно, что он живёт в квартире
№ 77, в его доме один подъезд, а на каждом этаже по четыре квартиры.
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ
А) площадь обложки паспорта
Б) площадь стола
В) площадь города Москва
Г) площадь баскетбольной площадки
ЗНАЧЕНИЯ
1) 0,8 кв. м
2) 50 кв. см
3) 2511 кв. км
4) 420 кв. м
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
В финальной части соревнований по толканию ядра каждый участник совершил 6 попыток.
Результаты спортсменов сведены в таблицу. Занятые ими места на пьедестале распределяются
по результатам лучшей попытки каждого спортсмена: чем дальше он толкнул ядро, тем лучше.
Фамилия
спортсмена
Результат попытки, м
№1
№2
№3
№4
№5
№6
Иванов
23
23
22
21,5
20,5
21
Петров
21
20,5
22
21,5
22
21,5
19,5
20,5
21,5
20
21
19
Сидоров
Какое место занял спортсмен Петров?
Ответ: __________
4
U
, где I – сила тока (в амперах), U – напряжеR
ние (в вольтах), R – сопротивление (в омах), найдите напряжение, если I = 5 А и R = 0,3 Ом.
Ответ дайте в вольтах.
Используя Закон Ома в виде формулы I =
Ответ: __________
5
В среднем из 1000 батареек, поступающих в продажу, 3 бракованные. Найдите вероятность
того, что одна случайно выбранная батарейка рабочая.
Ответ: __________
190
6
Цена электроэнергии по однотарифному счётчику составляет 5,7 рублей за кВт · ч. Цены по
двухтарифному счётчику: в дневное время – 6,9 рублей за кВт·ч, в ночное время – 2,6 рублей
за кВт· ч. Житель города тратит в месяц 100 кВт · ч в дневное время и 120 кВт· ч в ночное время. Рассчитайте сколько рублей сэкономит житель при использовании двухтарифного счётчика
по сравнению с однотарифным за 12 месяцев (один год). В ответ запишите сумму в рублях.
Ответ: __________
7
На графике показано изменение скорости ветра в зависимости от времени суток. По горизонтали – время суток в часах, по вертикали – скорость ветра в м/c. Пользуясь графиком, поставьте
в соответствие каждому интервалу времени характеристику на этом интервале.
16
12
8
4
0
0
3
ИНТЕРВАЛЫ
А) с 0 до 6 часов
Б) с 6 до 12 часов
В) с 12 до 18 часов
Г) с 18 до 24 часов
6
9
12
15
18
21
24
ХАРАКТЕРИСТИКИ
1) скорость ветра снизилась на 8 м/c за 3 часа
2) скорость ветра не превышала 5 м/c
3) скорость ветра сначала увеличивалась, а затем
была постоянной
4) скорость ветра увеличивалась
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
Если проехать под камерой на автомобиле, превысив скорость, то по почте придёт штраф.
Выберете утверждения, являющиеся верными при описанных условиях.
1) Если по почте пришёл штраф, то вы превысили скорость под камерой на автомобиле.
2) Если по почте не пришёл штраф, то вы не превышали скорость под камерой на автомобиле.
3) Если вы не превышали скорость под камерой на автомобиле, то по почте не придёт штраф.
4) Если вы проехали под камерой, превысив скорость, с выключенными фарами, то по почте
придёт штраф.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
191
9
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в
квадратных сантиметрах.
Ответ: __________
1м
10 В кадастровом плане квартиры указано, что прямоугольная комната имеет площадь 24 м2. Хозяин
квартиры решил сделать ремонт. При точном замере лазерным дальномером оказалось, что длина
комнаты 8,02 м, а ширина 3,1 м. На сколько квадратных метров отличается реальная площадь
комнаты от указанной в кадастровом плане?
Ответ: __________
11 При строительстве дома используют пеноблоки кубической формы двух размеров. Объём большего пеноблока в 27 раз отличается от объёма пеноблока меньшего размера. Во сколько раз
отличаются площади поверхности этих пеноблоков?
Ответ: __________
12
Основания равнобедренной трапеции равны 10 и 22. Острый
угол при основании равен 30°. Найдите квадрат боковой стороны
трапеции.
Ответ: __________
13 Площадь наибольшего сечения шара равна 10. Найдите площадь
поверхности шара.
Ответ: __________
14 Найдите значение выражения ( 8482 − 482 ) : 896 .
Ответ: __________
15 Цена акций компании 20% и составила 6000 рублей. Сколько рублей стоили акции до повышения цены?
Ответ: __________
16 Найдите значение выражения (2 ⋅ 103 ) ⋅ (2,1 ⋅ 10−1 ) .
Ответ: __________
192
17 Решите уравнение
19 + 5 x =
2.
Ответ: __________
18 Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого
столбца. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А)
2
( x − 3)
<0
x −1
Б) 2− x < 0,5
РЕШЕНИЯ
1) (1; +∞)
2) (1;3)
В) log 3 x > 1
3) (3; +∞)
Г) ( x − 1)( x − 3) < 0
4) (−∞;1)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Приведите пример шестизначного натурального числа, которое записывается только цифрами
1 и 2 и делится на 24. В ответе укажите какое-нибудь одно такое число.
Ответ: __________
20 Первую половину пути автомобиль двигался с скоростью 30 км/ч. Вторую половину пути он
ехал со скоростью в три раза больше. Найдите среднюю скорость автомобиля на всем пути.
Ответ дайте в км/ч.
Ответ: __________
21 В секции по боксу занимается 8 человек. Тренеру необходимо отобрать четыре человека для
участия в городских соревнованиях. Сколькими способами он может это сделать?
Ответ: __________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
193
ВАРИАНТ № 19
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Найдите, на каком этаже находится квартира Алексея, если известно, что он живёт в квартире
№ 35, в его доме один подъезд, а на каждом этаже по четыре квартиры.
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ
А) площадь листа бумаги
Б) площадь поверхности тумбочки
В) площадь города Екатеринбург
Г) площадь футбольной площадки
ЗНАЧЕНИЯ
1) 7140 кв. м
2) 3600 кв. см
3) 1112 кв. км
4) 0,06 кв. м
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
3
А
Б
В
Г
В финальной части соревнований по метанию копья каждый участник совершил 6 попыток.
Результаты спортсменов сведены в таблицу. Занятые ими места на пьедестале распределяются
по результатам лучшей попытки каждого спортсмена: чем дальше он метнул копье, тем лучше.
Результат попытки, м
Фамилия
спортсмена
№1
№2
№3
№4
№5
№6
Иванов
83
83
82
81,5
80,5
81
Петров
81
80,5
82
81,5
82
81,5
Сидоров
89,5
80,5
81,5
80
81
89
Какое место в итоге занял спортсмен Сидоров?
Ответ: __________
4
U
, где I – сила тока (в амперах), U – напряжение (в вольтах), R –
R
сопротивление (в омах), найдите сопротивление, если I = 5 А и U = 12 В. Ответ дайте в омах.
Используя закон Ома I =
Ответ: __________
5
В среднем из 1000 батареек, поступающих в продажу, 2 бракованные. Найдите вероятность
того, что одна случайно выбранная батарейка рабочая.
Ответ: __________
194
6
Цена электроэнергии по однотарифному счётчику составляет 5 рублей за кВт∙ч. Цены по двухтарифному счётчику: в дневное время – 7 рублей за кВт∙ч, в ночное время – 2 рубля за кВт∙ч.
Житель города тратит в месяц 80 кВт∙ч в дневное время и 110 кВт∙ч в ночное время (в месяц).
Рассчитайте сколько рублей сэкономит житель при использовании двухтарифного счётчика по
сравнению с однотарифным за 12 месяцев (один год). В ответ запишите сумму в рублях. .
Ответ: __________
7
На графике показано изменение скорости ветра в зависимости от времени суток. По горизонтали – время суток в часах, по вертикали – скорость ветра в м/c. Пользуясь графиком, поставьте
в соответствие каждому интервалу времени характеристику на этом интервале.
16
12
8
4
0
3
6
9
ИНТЕРВАЛЫ
12
15 18
21 24
ХАРАКТЕРИСТИКИ
А) с 0 до 6 часов
Б) с 6 до 12 часов
В) с 12 до 18 часов
Г) с 18 до 24 часов
1)
2)
3)
4)
скорость
скорость
скорость
скорость
ветра
ветра
ветра
ветра
увеличилась на 8 м/c за 3 часа
увеличилась на 2 м/c за 6 часов
была минимальной
уменьшалась
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
Если студент сдаёт сессию без троек, то на следующий семестр ему назначается стипендия.
Так же некоторые студенты получают социальную стипендию независимо от результатов учёбы.
Выберите утверждения, которые верны при указанных данных.
1)
2)
3)
4)
Если
Если
Если
Если
сессия сдана на отлично, то студенту будет назначена стипендия.
студент получит тройку, то студенту не будет назначена стипендия.
стипендия не была назначена, то сессия не сдана без троек.
стипендия была назначена, то сессия сдана без троек
В ответ запишите номера выбранных утверждений без пробелов и запятых.
Ответ: __________
195
9
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в
квадратных сантиметрах.
Ответ: __________
1 см
м
10 В кадастровом плане квартиры указано, что прямоугольная комната имеет площадь 27 м2. Хозяин квартиры решил сделать ремонт. При точном замере лазерным дальномером оказалось, что
длина комнаты 9,02 м, а ширина 3,01 м. На сколько квадратных метров отличается реальная
площадь комнаты от указанной в кадастровом плане?
Ответ: __________
11 При строительстве дома используют пеноблоки кубической формы двух размеров. Объём большего пеноблока в 64 раза отличается от объёма пеноблока меньшего размера. Во сколько раз
отличаются площади поверхности этих пеноблоков?
12 Основания равнобедренной трапеции равны 10 и 16. Острый угол при
основании равен 30°. Найдите квадрат боковой стороны трапеции.
Ответ: __________
13 Площадь наибольшего сечения шара равна 20. Найдите площадь поверхности шара.
Ответ: __________
14 Найдите значение выражения (242 − 142 ) :100 .
Ответ: __________
15 Цена акций компании упала на 25% и составила 9000 рублей. Сколько рублей стоили акции
до повышения цены?
Ответ: __________
16 Найдите значение выражения (2,5 ⋅ 103 ) ⋅ (3,4 ⋅ 10−1 ) .
Ответ: __________
196
17 Решите уравнение
10 − x =
3.
Ответ: __________
18 Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого
столбца. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А)
2
( x − 5)
<0
x−2
Б) 2− x < 0, 25
РЕШЕНИЯ
1) (2; +∞)
2) (2;5)
В) log 5 x > 1
3) (5; +∞)
Г) ( x − 2)( x − 5) < 0
4) (−∞;2)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Приведите пример шестизначного натурального числа, которое записывается только цифрами
1 и 2 и делится на 72. В ответе укажите какое-нибудь одно такое число.
Ответ: __________
20 Первую половину пути автомобиль двигался с скоростью 30 км/ч. Вторую половину пути он
ехал со скоростью в три раза больше. Найдите среднюю скорость автомобиля на всем пути.
Ответ дайте в км/ч.
Ответ: __________
21
В секции по боксу занимается 7 человек. Тренеру необходимо отобрать четыре человека для
участия в городских соревнованиях. Сколькими способами он может это сделать?
Ответ: __________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
197
ВАРИАНТ № 20
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Стоимость проездного билета на месяц составляет 1200 рублей, а стоимость билета на одну
поездку – 52 рубля. Петр купил проездной и сделал за месяц 40 поездок. На сколько рублей
больше он бы потратил, если бы каждый раз покупал билет на одну поездку?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) скорость света
Б) скорость самолёта
В) скорость автомобиля
Г) скорость муравья
1)
2)
3)
4)
90 км/ч
600 км/ч
300 000 км/с
7 см/c
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На рисунке точками показано суточное количество осадков, выпавших в городе. По горизонтали указаны числа месяца, по вертикали – количество осадков, выпавших за соответствующий
день, в миллиметрах.
Количество осадков, мм
7
6
5
4
3
2
1
03
4
5
6
7
8
9
10 11 12 13 14 15
Определите по графику, какого числа впервые выпало 4 миллиметра осадков.
Ответ: __________
198
4
Количество теплоты (в джоулях) выделяемое на проводнике можно вычислить по формуле
Q = I 2 Rt , где I – сила тока (в амперах), R – сопротивление (в омах), t – время (в секундах).
Пользуясь формулой, найдите сопротивление, если I = 2А, R = 5 Ом, t = 10 c. Ответ дайте в
джоулях
Ответ: __________
5
На чемпионате по биатлону выступают 25 спортсменов, среди них 10 спортсменов из России.
Порядок старта гонки определяется жеребьёвкой. Найдите вероятность того, что первым будет
стартовать спортсмен из России.
Ответ: __________
6
Три фирмы предлагают услуги по грузоперевозкам. Стоимость услуг, предоставляемых фирмами, приведены в таблице. Необходимо перевезти 10 тонн груза на 500 км. Сколько рублей
нужно заплатить за самую дешёвую перевозку в одной из этих фирм?
Перевозчик
Стоимость перевозки одним
грузовиком (руб. на 100 км)
Грузоподъёмность грузовика
(тонн)
1
2500
3
2
3300
4
3
8500
12
Ответ: __________
7
А)
А)
На рисунках изображены графики функций. Установите соответствие между графиками функций
и значениями их производных.
ГРАФИКИГРАФИКИ
ФУНКЦИЙ
ФУНКЦИЙ
ГРАФИКИ ФУНКЦИЙ
В)
Б)
В)
В)
Б)
Б)
А)
Г)
Г)
Г)
y
y
y
y
y
y
y
y
y
y
y
y
1
1
0 1
0 1
1
1
1
0 1
0 1
1
1
1
0 1
0 1
1
1
1
0 1
0 1
1
0x 1
x
x
0x 1
x
x
0x 1
x
x
0x 1
x
ЗНАЧЕНИЯ ПРОИЗВОДНЫХ
1) –4
2) 5
3) 4
4) –2
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
199
x
8
В классе учатся двадцать учеников, из них 12 учеников посещают дополнительные занятия по
математике, а 10 человек – дополнительные занятия по физике. Выберете утверждения, которые
являются верными при описанных условиях.
1) Нет ученика, который бы не посещал дополнительные занятия.
2) Найдется хотя бы два ученика, которые посещают дополнительные занятия, как по физике,
так и по математике.
3) Если ученик посещает дополнительные по математике, он обязательно посещает дополнительные по физике.
4) Не найдется 12 человек, которые посещают дополнительные занятия по двум предметам.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
9
Найдите площадь фигуры, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных
сантиметрах.
Ответ: __________
1 см
м
10 Какой наименьший угол образуют минутная и часовая стрелки часов в 4 часа дня? Ответ дайте
в градусах.
Ответ: __________
11 Найдите полную площадь поверхности многогранника, изображенного на рисунке.
1
1
2
Ответ: __________
3
2
12 Площадь параллелограмма KLMN равна 100. Точка А – середина стороны MN. Найдите площадь
треугольника KAN.
Ответ: __________
200
13
Объём конуса равен 54π , а его высота равна 6. Найдите радиус
основания конуса.
Ответ: __________
2
1
14 Найдите значение выражения 1 + 3 + 5 .
3
3
Ответ: __________
15 На подготовительных курсах английский язык изучают 15 учащихся, что составляет 5% от всех
учащихся на подготовительных курсах. Сколько учащихся на подготовительных курсах?
Ответ: __________
16 Найдите значение выражения 52 + log5 6 .
Ответ: __________
17 Решите уравнение
3 x + 27 =
6.
Ответ: __________
18 На координатной прямой отмечена число a. Установите соответствие между отрезками из правого столбца, которым эти числа принадлежат.
am
–1
0
1
ТОЧКИ
А) 5 − a
1) [1;2]
Б) a 2 + 2
2) [2;3]
В)
à+2
2
Г) − 1
à
2
ЧИСЛА
3) [3;4]
4) [4;5]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Приведите пример пятизначного числа, кратного 18, любые две соседние цифры которого отличаются на 3. В ответе укажите какое-нибудь одно такое число.
Ответ: __________
201
20 Бассейн наполняется через две трубы. Если открыть только первую трубу, бассейн наполнится
за 40 минут. Если же открыть только вторую, то за 60 минут соответственно. За сколько минут
наполнится бассейн, если открыть одновременно обе трубы?
Ответ: __________
21 На пяти карточках написаны цифры 1, 2, 3, 4, 5 соответственно. Сколько различных трехзначных
чисел можно составить их этих карточек?
Ответ: __________
!
202
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 21
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Стоимость проездного билета на месяц составляет 1100 рублей, а стоимость билета на одну
поездку – 51 рубль. Василий купил проездной и сделал за месяц 35 поездок. На сколько рублей
больше он бы потратил, если бы каждый раз покупал билет на одну поездку?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) скорость звука
Б) скорость самолёта
В) скорость мотоциклиста
Г) скорость ползущего жука
1)
2)
3)
4)
700 км/ч
343 м/с
120 км/ч
20 см/c
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На рисунке точками показано суточное количество осадков, выпавших в городе. По горизонтали указаны числа месяца, по вертикали – количество осадков, выпавших за соответствующий
день, в миллиметрах.
Количество осадков, мм
7
6
5
4
3
2
1
03
4
5
6
7
8
9
10 11 12 13 14 15
Определите по графику, какого числа впервые выпало 6 мм осадков.
Ответ: __________
4
Количество теплоты (в джоулях) выделяемое на проводнике можно вычислить по формуле
Q = I 2 Rt , где I – сила тока (в амперах), R – сопротивление (в омах), t – время (в секундах).
Пользуясь формулой, найдите сопротивление, если I = 3А, R = 4 Ом, t = 5 c. Ответ дайте в
джоулях
Ответ: __________
203
5
На чемпионате по биатлону выступают 25 спортсменов, среди них 15 спортсменов из России.
Порядок старта гонки определяется жеребьёвкой. Найдите вероятность того, что первым будет
стартовать спортсмен из России.
Ответ: __________
6
Три фирмы предлагают услуги по грузоперевозкам. Стоимость услуг, предоставляемых фирмами,
приведены в таблице. Необходимо перевезти 10 тонн груза на 500 км. Сколько рублей нужно
заплатить за самую дешёвую перевозку в одной из этих фирм?
Номер фирмы
Стоимость перевозки одним
грузовиком (руб. на 100 км)
Грузоподъёмность
грузовика (тонн)
1
3500
3
2
4300
4
3
10500
12
Ответ: __________
7
На рисунках изображены графики функций. Установите соответствие между графиками функций
и значениями их производных.
ГРАФИКИ ПРОИЗВОДНЫХ
А)
Б)
В)
y
y
1
0 1
x
y
y
1
0 1
Г)
1
1
x
0 1
x
ХАРАКТЕРИСТИКИ
1) x = 2 является точкой максимума функции
2) x = –1 является точкой минимума функции
3) функция убывает только на промежутке ( − ∞; 2]
4) функция возрастает только на промежутке ( − ∞; − 1]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
204
А
Б
В
Г
0 1
x
8
Александр Сергеевич был в отпуске 7 дней на курорте. Три раза он выезжал на экскурсии и
шесть раз ходил на море. За один день он мог и съездить на экскурсию, и сходить на море, а мог
никуда не ездить и не ходить. Выберите утверждения, которые верны при указанных условиях..
1) Не может оказаться, что Александр Сергеевич 4 дня ходил на море и ездил на экскурсии.
2) Было 2 дня, когда Александр Сергеевич ходил и на море и ездил на экскурсии.
3) Было 2 дня, когда Александр Сергеевич никуда не ходил и не ездил.
4) Если Александр Сергеевич ходил на море, то в этот день он был на экскурсии.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
9
Найдите площадь трапеции, изображённой на клетчатой бумаге с
размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
Ответ: __________
1 см
м
10 Какой наименьший угол образуют минутная и часовая стрелки часов в 7 часов утра? Ответ
дайте в градусах.
Ответ: __________
11 Найдите полную площадь поверхности многогранника, изображенного на рисунке.
2
2
2
Ответ: __________
4
3
12 Площадь параллелограмма KLMN равна 50. Точка А – середина стороны MN. Найдите площадь
треугольника KAN.
Ответ: __________
205
13 Объём конуса равен 12π , а его высота равна 3. Найдите радиус основания конуса.
Ответ: __________
1 1
14 Найдите значение выражения 2 : .
3 3
Ответ: __________
15
На подготовительных курсах математику изучают 66 учащихся, что составляет 30% от всех
учащихся на подготовительных курсах. Сколько учащихся на подготовительных курсах?
Ответ: __________
16 Найдите значение выражения 51+ log5 3 .
Ответ: __________
17 Решите уравнение
2 x + 3 =.
5
Ответ: __________
18 На координатной прямой отмечены числа a и b. Установите соответствие между указанными
числами из левого столбца и отрезками из правого столбца, которым эти числа принадлежат.
аn
–3
–2
–1
ЧИСЛА
А) ab
Б) ab+ b
a
b
В)
a
b
b
1a
Г) + ba
a
b
a
0
1
bm
2
3
x
ОТРЕЗКИ
1) [ 0;1]
2) [1;2]
3) [ 2;3]
4) [3;4]
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Приведите пример пятизначного числа, кратного 22, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.
Ответ: __________
206
20
Сплав меди и цинка весом 20 кг содержит 30% меди. Добавили 22 кг цинка. Сколько нужно
добавить меди, чтобы в сплаве стало 60% цинка? Ответ дайте в килограммах.
Ответ: __________
21 На пяти карточках написаны цифры 1, 2, 3, 4, 5. Сколько различных двухзначных чисел можно
составить из этих карточек?.
Ответ: __________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
207
ВАРИАНТ № 22
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Пациенту прописали лекарство, которое нужно пить по одной таблетке 3 раза в день в течение
месяца (30 дней). В одной упаковке 12 таблеток. Сколько упаковок лекарства надо купить,
чтобы его хватило на месяц?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ
А) площадь Тихого океана
Б) радиус планеты Земля
В) масса планеты Земля
Г) объём воды в мировом океане
ЗНАЧЕНИЯ
1)
2)
3)
4)
165 ⋅ 106 км2
1,3 ⋅ 109 км3
6 ⋅ 1024 кг
6, 4 ⋅ 103 км
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показано месячное количество осадков, выпавших в городе. По горизонтали
указаны месяца года, по вертикали – количество осадков, выпавших за соответствующий день,
в миллиметрах. Определите по диаграмме общее количество осадков, выпавших в четвертом
квартале. Ответ дайте в миллиметрах.
30
25
20
15
10
5
0
январь февраль март
Ответ: __________
208
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
4
Длина медианы mb , проведенной к стороне b треугольника со сторонами a, b и с вычисляется
по формуле m=
b
b = 12 и c = 5.
1
2a 2 + 2c 2 − b 2 . Найдите медиану mb треугольника со сторонами a = 13 ,
2
Ответ: __________
5
Какова вероятность, что число, составленное из двух последних цифр случайного номера телефона, делится на 3? Ответ округлите до десятых.
Ответ: __________
6
Клиент выбирает тариф для мобильной связи из трёх возможных. Условия тарифов представлены в таблице. Клиент выбрал наиболее дешёвый тариф, исходя из того, что длительность
его телефонных разговоров всегда составляет 500 минут в месяц. Сколько рублей за месяц он
будет платить за мобильную связь?
Тариф
Абонентская плата
Плата за 1 минуту разговора
А
200 руб. в месяц
0,1 руб.
Б
250 руб. за 400 мин. в месяц
0,2 руб. за 1 мин. при превышении 400 мин. в месяц.
В
400 руб. в месяц
нет
Ответ: __________
7
2
На рисунках изображены графики производных функций вида y = ax + bx + c . Установите соответствие между графиками производных функций и характеристиками функций.
ГРАФИКИ ПРОИЗВОДНЫХ
А)
Б)
В)
Г)
y
y
y
y
1
0 1
1
x
0 1
1
x
0 1
1
x
0 1
x
ХАРАКТЕРИСТИКИ
1) x = 1 является точкой минимума
2) x = 0 является точкой максимума функции
3) функция возрастает на промежутке [ − 2;1]
4) функция убывает на промежутке [ − 4; 2]
209
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
Работник выходит из дома на работу в 7 утра. Если он вышел вовремя, то он успевает доехать
до работы на автобусе. Если работник выходит позже 7 утра, то он всегда едет на работу на
такси. Выберите утверждения, которые верны при указанных условиях.
1) Если работник вышел на работу в 7-30 утра, то он едет на такси.
2) Если работник вышел на работу в 6-30 утра, то он едет на автобусе.
3) Если работник вышел на работу в 7-30 утра, то он едет на автобусе.
4) Если работник вышел на работу в 7 утра, то он может поехать как на автобусе, так и на такси.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
9
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте
в квадратных сантиметрах.
Ответ: __________
10 Хозяин квартиры решил выложить три стены ванной комнаты плиткой. Пол ванной комнаты
имеет форму квадрата со стороной 2 м, а высота потолков – 3 м. Какую площадь собирается
выло-жить плиткой хозяин квартиры? Ответ дайте в квадратных метрах.
Ответ: __________
11 Бокал для напитков имеет коническую форму высотой 93 мм. В бокал налили воду до краёв.
Затем воду перелили в чашку, имеющую цилиндрическую форму. На какой высоте будет вода в
чашке, при условии, что радиус верхней части бокала равен радиусу основания чашки? Ответ
дайте в миллиметрах.
Ответ: __________
12 Высоты параллелограмма равны 20 и 24, а меньшая из его сторон
равна 30. Найдите большую сторону параллелограмма.
Ответ: __________
210
13 Дана правильная четырехугольная пирамида, все ребра которой равны 12. Через середины боковых ребер провели сечение пирамиды.
Найдите его площадь.
Ответ: __________
π
7π
14 Найдите значение выражения 2 3 ⋅ sin ⋅ cos .
6
6
Ответ: __________
15 В канцелярском магазине при покупке товара на сумму более 1000 рублей магазин делает скидку
7% от стоимости всей покупки. Покупатель собирается купить 70 ручек по 15 рублей за ручку.
Сколько рублей он заплатит за всю покупку?
Ответ: __________
16 Найдите sin x , если cos x = 0,6 и π < x < 2π .
Ответ: __________
17 Решите уравнение 1
3
Ответ: __________
x −5
= 92 x + 4 .
18 На координатной прямой отмечены точки A, B, C и D . Каждой точке соответствует одно из
чисел в правом столбце. Установите соответствие между указанными точками и числами.
A
0
B C
1
2
ТОЧКИ
3
D
4
5
6
ЧИСЛА
10
А) A
1)
Б) B
2) log 3 2
В) C
3) π + 2
−1
12
4)
33
В таблице под каждой буквой укажите соответствующий номер.
Г) D
Ответ:
А
Б
В
Г
19 Трёхзначное число, первая цифра которого 9, разделили на сумму квадратов его цифр. В остатке
получили 0. Найдите исходное число. В ответ запишите какое-нибудь одно такое число.
Ответ: __________
211
20 В 10 часов утра навстречу друг другу из пунктов А и Б выехали мотоциклист и велосипедист.
Через один час после начала движения они встретились, и через 20 минут после встречи мотоциклист был в пункте Б. Во сколько часов прибыл в пункт А велосипедист, если во время
движения каждый из них двигался с постоянной скоростью? Ответ дайте в часах.
Ответ: __________
21 Сколько существует различных треугольников, у каждого из которых длины сторон принимают
одно из значений – 5, 6, 7, 8?
Ответ: __________
!
212
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 23
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Пациенту прописали лекарство, которое нужно пить по одной таблетке 2 раза в день в течение
месяца (30 дней). В одной упаковке 7 таблеток. Сколько упаковок лекарства надо купить, чтобы
его хватило на месяц?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ А) площадь Мирового океана
Б) радиус планеты Марс
В) масса планеты Меркурий
Г) объём воды в озере Байкал
ЗНАЧЕНИЯ
1)
2)
3)
4)
23,6 тыс. км3
3,38 ⋅ 103 км
3, 26 ⋅ 1023 кг
3,61 ⋅ 105 км2
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показано месячное количество осадков, выпавших в городе. По горизонтали
указаны месяца года, по вертикали – количество осадков, выпавших за соответствующий день,
в миллиметрах.
30
25
20
15
10
5
0
январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
Определите по диаграмме разницу между наибольшим и наименьшим месячными показателями
в первом полугодии. Ответ дайте в миллиметрах.
Ответ: __________
213
4
Длина медианы mc , проведенной к стороне с треугольника со сторонами a, b и с вычисляется
по формуле m=
c
b = 13 и c = 5 .
1
2a 2 + 2b 2 − c 2 . Найдите медиану mc треугольника со сторонами a = 12 ,
2
Ответ: __________
5
Какова вероятность, что число, составленное из двух последних цифр случайного номера телефона, делится на 5? Ответ округлите до десятых.
Ответ: __________
6
Клиент выбирает тариф для мобильной связи из трёх возможных. Условия тарифов представлены в таблице. Клиент выбрал наиболее дешёвый тариф, исходя из того, что длительность
его телефонных разговоров всегда составляет 700 минут в месяц. Сколько рублей за месяц он
будет платить за мобильную связь?
Тариф
Абонентская плата
Плата за 1 минуту
разговора
А
250 руб. в месяц
0,1 руб.
Б
300 руб. за 400 мин. в месяц
0,2 руб. за 1 мин. при
превышении 400 мин.
в месяц.
В
500 руб. в месяц
нет
Ответ: __________
7
На рисунке изображён график производной функции. Установите соответствие между свойствами
функции и отрезками, на которых они выполняются..
y
1
0 1
ОТРЕЗКИ
214
x
СВОЙСТВА
А) [− 5; − 3] 1) функция имеет точку максимума
Б) [− 3; 0] 2) функция убывает
В) [0; 4] 3) функция возрастает
Г) [4; 6] 4) функция имеет точку минимума
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
Максим сдавал ЕГЭ по четырём предметам – математика, русский язык, физика, информатика.
Средний балл по всем предметам составил 77 баллов. Самый низкий результат он показал по
математике – 62 балла. Выберите утверждения, которые верны при указанных условиях.
1) Средний балл у Максима по трём экзаменам – русскому языку, физике и информатике, составил 82 балла.
2) Минимальный балл Максима из трёх экзаменов без математики равен 80.
3) Ни по одному экзамену Максим не набрал 100 баллов.
4) По какому-то предмету Максим получил больше 80 баллов.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
9
Найдите площадь треугольника, изображённого на клетчатой бумаге с
размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
Ответ: __________
1 см
м
10 Хозяин квартиры решил выложить три стены ванной комнаты плиткой. Пол ванной комнаты
имеет форму квадрата со стороной 2,5 м, а высота потолков – 3,5 м. Какую площадь собирается
выложить плиткой хозяин квартиры? Ответ дайте в квадратных метрах.
Ответ: __________
11 Бокал для напитков имеет коническую форму высотой 84 мм. В бокал налили воду до краёв.
Затем воду перелили в чашку, имеющую цилиндрическую форму. На какой высоте будет вода
в чашке при условии, что радиус верхней части бокала равен радиусу основания чашки? Ответ
дайте в миллиметрах.
Ответ: __________
12 Стороны параллелограмма равны 18 и 15. Высота, опущенная на большую из этих сторон, равна 10. Найдите высоту,
опущенную на меньшую сторону параллелограмма.
Ответ: __________
215
S
13 Дана правильная четырехугольная пирамида, все ребра которой равны 14. Через середины боковых ребер провели сечение пирамиды.
Найдите его площадь.
E
C
D
Ответ: __________
B
7π
π
14 Найдите значение выражения 2 ⋅ cos 2
− sin 2 .
6
6
Ответ: __________
А
15 Цена на книгу была повышена на 24% и составила 899 рублей. Сколько стоила книга до повышения цены? В ответе укажите первоначальную стоимость книги в рублях.
Ответ: __________
16 Найдите sin x , если cos x = −0,8 и
π
<x<π.
2
Ответ: __________
17 Решите уравнение 23− x = 85− 2 x .
Ответ: __________
18
На координатной прямой отмечены точки A, B, C и D . Каждой точке соответствует одно из
чисел в правом столбце. Установите соответствие между указанными точками и числами.
A
0
1
B C
2
ТОЧКИ
А) A
D
3
4
5
6
ЧИСЛА
1) log 3 33
Б) B
2)
27
В) C
3)
3 +1
Г) D
14
4)
23
−1
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Трёхзначное число, первая цифра которого 5, разделили на сумму квадратов его цифр. Получили 14. Найдите исходное число.
Ответ: __________
216
20 Два пешехода вышли в 10 часов утра навстречу друг другу из пунктов А и Б. Через два часа
после начала движения они встретились, а еще через час пешеход, вышедший из пункта А прибыл в пункт Б. Во сколько часов прибыл в пункт А пешеход, вышедший из пункта Б, если во
время движения каждый из пешеходов двигался с постоянной скоростью? Ответ дайте в часах.
Ответ: __________
21 Сколько существует различных треугольников, у каждого из которых длины сторон принимают
одно из значений – 5, 6, 7, 8, 9?
Ответ: __________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
217
ВАРИАНТ № 24
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Установка счётчиков воды стоит 5700 рублей. До установки счётчиков жилец платил за воду
1400 рублей в месяц. После установки счётчиков жилец стал платить 800 рублей в месяц. За
какое наименьшее целое количество месяцев окупится установка счётчиков?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ А) длительность полнометражного фильма
Б) время обращения Земли вокруг Солнца
В) длительность перелёта Москва-Владивосток
Г) длительность урока в школе
ЗНАЧЕНИЯ
1) 45 мин
2) 9 часов
3) 365 суток
4) 2 часа
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме представлена средняя продолжительность жизни некоторых животных. По вертикали
указана средняя продолжительность жизни в годах, по горизонтали – названия животных.
30
25
20
15
10
5
0
Свинья
Кошка
Корова
Лошадь
Коза
Собака
Хомяк
Пользуясь диаграммой, определите, во сколько раз средняя продолжительность жизни кошек
больше, чем средняя продолжительность жизни хомяков.
Ответ: __________
218
4
d1d 2 sin α
, где d1 и
2
d 2 – длины диагоналей четырёхугольника, α – угол между диагоналями. Пользуясь формулой,
Площадь выпуклого четырёхугольника можно вычислить по формуле S =
найдите угол между диагоналями, если S = 14 , d1 = 7 , d 2 = 8 . Ответ дайте в градусах.
Ответ: __________
5
Уличный фонарь содержит две лампы. Вероятность перегорания одной лампы в течение года
равна 0,4. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Ответ: __________
6
Шкаф–купе можно купить в кредит в трёх мебельных магазинах. Условия продажи представлены в таблице. Определите, в каком из магазинов покупка обойдется дешевле всего (с учётом
переплаты). В ответе укажите стоимость покупки в рублях.
Магазин
Цена
(руб.)
Первоначальный взнос
(в % от стоимости)
Срок кредита
(мес.)
Сумма
ежемесячного
платежа (руб.)
1
72300
20
6
11040
2
72600
25
6
9840
3
75000
25
12
4860
Ответ: __________
7
Установите соответствие между функциями в левом столбце и их производными в точке
x0 = 1 в правом. Запишите последовательность цифр из правого столбца, соответствующих
буквам из левого столбца.
ФУНКЦИИ
1 2
x + 6x − 3
2
Б) y = 2 x 2 − 4 x + 11
1
В) y =
− x 2 − 5 x + 17
2
−6 x 2 + 11x + 18
Г) y =
А) y =
ЗНАЧЕНИЯ ПРОИЗВОДНЫХ В ТОЧКЕ x0 = 1
1) 0
2) 8
3) –1
4) –6
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
В одном шкафу меньше книг, чем во втором. В третьем шкафу больше книг, чем во втором.
В четвёртом шкафу больше книг, чем в первом, но меньше, чем в третьем. Выберите утверждения, которые верны при указанных условиях.
1)
2)
3)
4)
В первом шкафу меньше книг, чем в четвёртом.
В третьем шкафу больше всего книг.
Среди этих четырёх шкафов есть три с одинаковым числом книг.
В четвертом шкафу лежит одна книга.
В ответ запишите номера выбранных утверждений без пробелов и запятых.
Ответ: __________
219
9
Найдите площадь четырехугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
Ответ: __________
1 см
м
10 Дачный участок имеет форму прямоугольника со сторонами
28 м и 37 м. Дом, расположенный на участке, имеет форму
прямоугольника, стороны которого равны 9 м и 4 м. Найдите
площадь свободной части участка (без дома). Ответ дайте в
квадратных метрах.
28 м
4м
37 м
9м
Ответ: __________
11 Подарок на день рождения решили упаковать в коробку, имеющую форму куба с ребром 4 см.
Коробку нужно обклеить саружи со всех сторон подарочной бумагой. Найдите площадь поверхности, которую необходимо обклеить. Ответ дайте в квадратных сантиметрах.
Ответ: __________
C
12
В равнобедренном треугольнике AC
= BC
= 4 , угол при вершине С
равен 30° . Найдите высоту АН.
H
Ответ: __________
A
13
Сторона основания правильной шестиугольной пирамиды равна 24,
боковое ребро равно 37. Найдите площадь боковой поверхности пирамиды.
Ответ: __________
220
B
14 Найдите значение выражения −2 3 cos1110°.
Ответ: __________
15 Товар стоит 650 рублей. После снижения цены товар стал стоить 507 рублей. На сколько процентов была снижена цена?
Ответ: __________
16 Найдите log b 5 a , если log a b = 1 .
15
Ответ: __________
17 Решите уравнение log 9 ( x + 6) =
0,5 .
Ответ: __________
18 На координатной прямой точками отмечены числа A, B, C и D.
A
B C
D
ТОЧКИ
ЧИСЛА
А) А
1) 0,09
Б) B
2) −
В) C
Г) D
6
91
3) −1,173
27
4)
29
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
19
А
Б
В
Г
Найдите наибольшее трёхзначное число, которое меньше 350, если произведение его цифр
равно 42.
Ответ: __________
20 Теплоход прошёл против течения реки 120 км и вернулся в пункт отправления, затратив на
обратный путь на 5 часов меньше. Найдите скорость течения реки, если скорость теплохода в
стоячей воде равна 10 км/ч. Ответ дайте в км/ч.
Ответ: __________
221
21 При подготовке к ЕГЭ по математике выяснилось, что среди 23 учеников 11 класса 3 ученика
пишут тренировочную работу всегда только на 5, 10 учеников – на 4 или 5, а другие 10 учеников
могут получить за работу 3, 4 или 5. Сколько учеников из этого класса достаточно посадить в
аудиторию, чтобы наверняка хотя бы одна из работ, написанных ими в этой аудитории, была
оценена пятёркой?
Ответ: __________
!
222
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 25
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Установка счётчиков воды стоит 4500 рублей. До установки счётчиков жилец платил за воду 900
рублей в месяц. После установки счётчиков жилец стал платить 500 рублей в месяц. За какое
наименьшее целое количество месяцев окупятся затраты на установку счётчиков?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ВЕЛИЧИНЫ
А) длительность одной серии сериала
Б) время обращения Земли вокруг своей оси
В) длительность моргания глаза человека
Г) длительность пары в университете
ЗНАЧЕНИЯ
1) 24 часа
2) 40 минут
3) 120 минут
4) 0,05 секунд
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме представлена средняя продолжительность жизни некоторых животных. По вертикали указана средняя продожительность жизни в годах, по горизонтали – названия животных.
30
25
20
15
10
5
0
Свинья
Кошка
Корова
Лошадь
Коза
Собака
Хомяк
Пользуясь диаграммой, найдите, сколько животных из перечисленных на диаграмме живут в
среднем не меньше 20 лет.
Ответ: __________
223
4
d1d 2 sin α
, где d1 и
2
d 2 – длины диагоналей четырёхугольника, α – угол между диагоналями. Пользуясь формулой,
Площадь выпуклого четырёхугольника можно вычислить по формуле S =
найдите угол между диагоналями, если S = 6 3 , d1 = 3 , d 2 = 8 . Ответ дайте в градусах.
Ответ: __________
5
Уличный фонарь содержит две лампы. Вероятность перегорания одной лампы в течение года
равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Ответ: __________
6
Шкаф-купе можно купить в кредит в трёх мебельных магазинах. Условия продажи представлены в таблице. Определите, в каком из магазинов покупка обойдётся дешевле всего (с учётом
пере-платы). В ответе укажите стоимость покупки в рублях.
Магазин
Цена
(руб.)
Первоначальный взнос
Срок
Сумма ежемесячно(в % от стоимости)
кредита (мес.) го платежа (руб.)
1
48200
20
6
7360
2
48400
25
6
6560
3
50000
25
12
3240
Ответ: __________
7
Установите соответствие между функциями в левом столбце и значениями их производных в
точке x0 = 1 в правом.
ФУНКЦИИ
А) y = 4 x 2 + 2 x − 15
−2 x 2 − 3 x + 13
Б) y =
y 8x2 − 5
В) =
−3 x 2 + 6 x − 19
Г) y =
ПРОИЗВОДНЫЕ В ТОЧКЕ x0 = 1
1)
2)
3)
4)
–7
10
0
11
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
224
А
Б
В
Г
Рядом растут четыре дерева: липа, берёза, ёлка и дуб. Липа ниже берёзы, а ёлка выше берёзы.
Дуб выше липы, но ниже ёлки. Выберите утверждения, которые верны при указанных условиях
1) Среди этих четырёх деревьев есть два одинаковых по высоте.
2) Дуб самый высокий из этих четырёх деревьев.
3) Липа самая низкая из этих четырёх деревьев.
4) Ёлка выше липы.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
9
Найдите площадь четырёхугольника, изображённого на клетчатой
бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных
сантиметрах.
Ответ: __________
1 см
м
45 м
10 Дачный участок имеет форму прямоугольника со сторонами 32 м
и 45 м. Дом, расположенный на участке, имеет форму квадрата,
со стороной 10 м. Найдите площадь свободной части участка (без
дома). Ответ дайте в квадратных метрах.
10 м
32 м
10 м
Ответ: __________
11 Подарок на день рождения решили упаковать в коробку, имеющую форму куба с ребром 5 см.
Коробку нужно обклеить снаружи подарочной бумагой. Найдите площадь поверхности, которую
необходимо обклеить. Ответ дайте в квадратных сантиметрах.
Ответ: __________
C
12 В равнобедренном треугольнике AC
= BC
= 2 2 , угол при вершине С
равен 45° . Найдите высоту АН.
Ответ: __________
H
A
B
13 Сторона основания правильной шестиугольной пирамиды равна 18,
боковое ребро равно 41. Найдите площадь боковой поверхности пирамиды.
Ответ: __________
225
14 Найдите значение выражения −12cos 600° .
Ответ: __________
15 Товар стоит 1300 рублей. После снижения цены товар стал стоить 1053 рубля. На сколько процентов была снижена цена?
Ответ: __________
1
1
16 Найдите log
og b aa8=b , если log b a = .
8
8
Ответ: __________
17 Решите уравнение log 25 ( x − 6) =
0,5 .
Ответ: __________
18 На координатной прямой точками A, B, C и D отмечены числа.
ТОЧКИ
А) А
Б) B
В) C
Г) D
ЧИСЛА
1) –2,8
86
2)
41
3) 3,3
59
4) −
18
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
19
А
Б
В
Г
Найдите наибольшее трёхзначное число, которое меньше 400, если произведение его цифр
равно 30.
Ответ: __________
20 Теплоход прошёл против течения реки 288 км и вернулся в пункт отправления, затратив на
обратный путь на 8 часов меньше. Найдите скорость течения реки, если скорость теплохода в
стоячей воде равна 15 км/ч. Ответ дайте в км/ч.
Ответ: __________
226
21 При подготовке к ЕГЭ по математике выяснилось, что среди 24 учеников 11 класса 7 учеников пишут тренировочную работу всегда только на 5, 8 учеников – на 4 или 5, а 9 учеников
могут получить за работу 3, 4 или 5. Сколько учеников из этого класса достаточно посадить
в аудиторию, чтобы наверняка хотя бы одна из работ, написанных ими в этой аудитории была
оценена пятёркой?
Ответ: __________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
227
ВАРИАНТ № 26
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Каждый день кафе «Сладкоежка» расходует 21 кг сахара, который закупает пакетами по 950 г.
На сколько дней хватит 500 пакетов сахара?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А) масса электронной клавиатуры
Б) продолжительность полярной ночи в Мурманске
В) длина реки Обь
Г) объём комнаты
1) 174 суток
2) 700 г
3) 75 м3
4) 3650 км
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показана среднемесячная температура воздуха в городе N за каждый месяц года.
По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. .
24
20
16
12
8
4
0 январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
–4
Определите по приведённой диаграмме наибольшую среднемесячную температуру в осенние
месяцы года. Ответ дайте в градусах Цельсия
Ответ: __________
228
4
Тело брошено вертикально вверх с высоты 28 метров. Пока тело не упало, высота, на которой
оно находится, описывается формулой h(t ) = 28 + 13t − 5t 2 , где h – высота в метрах, t – время в
секундах, прошедшее с момента броска. На какой высоте тело будет через 3 секунды?
Ответ: __________
5
Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле
равна 0,9. Найдите вероятность того, что он попал в мишень ровно два раза.
Ответ: __________
6
Для изготовления шкафов требуется заказать 60 одинаковых зеркал в одной из трёх фирм.
Площадь каждого зеркала 0,4 м2. В таблице приведены цены на зеркала, а также на резку зеркал
и шлифовку края. Сколько рублей будет стоить самый дешёвый заказ?
Фирма
Ценя зеркала
(рублей за 1 м2)
Резка и шлифовка
(рублей за одно зеркало)
А
800
160
Б
750
165
В
850
130
Ответ: __________
7
На рисунке изображён график функции f ( x) . Пользуясь графиком, поставьте в соответствие
каждому из указанных интервалов характеристику функции или её производной.
y
y = f(x)
1
–2
ИНТЕРВАЛ
А) (−2;1)
Б) (4; 7)
В) (−1; 5)
Г) (5;12)
0
1
12 x
ХАРАКТЕРИСТИКА
1)
2)
3)
4)
функция отрицательна на всём интервале
производная функции неотрицательна на всём интервале
функция положительна на всём интервале
производная функции неположительна на всём интервале
229
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
В вузы поступают только выпускники школ или колледжей. Выберите утверждения, которые
верны при указанных условиях.
1) Если человек окончил школу, то он поступит в вуз.
2) Если человек не окончил школу или колледж, то он не поступит в вуз.
3) Если человек не поступил в вуз, то он не окончил ни школы, ни колледжа.
4) Если человек поступил в вуз, то он окончил школу или колледж.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
9
Ответ: __________
10
Заповедник
На рисунке изображён план местности (шаг сетки плана
соответствует расстоянию 1 км на местности). Оцените,
скольким квадратным километрам равна площадь озера
«Долгое», изображённого на плане. Ответ округлите до
целого числа.
Оз. Долгое
Оз. Круглое
Между фонарём, высота которого равна 6 м, и вертикальной стеной стоит человек, ростом
1,8 м. Найдите расстояние от человека до фонаря, если высота тени, отбрасываемой человеком
на стену, равна 1 м, а расстояние от него до стены – 80 см. Ответ выразите в сантиметрах.
Ответ: __________
11 Однородный цилиндр с радиусом основания 8 см и высотой 10 см весит 1600 г. Сколько весит цилиндр с радиусом
основания 10 см и высотой 8 см, изготовленный из того
же материала? Ответ выразите в граммах.
Ответ: __________
12 Стороны параллелограмма равны 3 и 15. Высота, опущенная на меньшую сторону, равна 8.
Найдите высоту, опущенную на большую сторону параллелограмма.
Ответ: __________
230
13
Объем куба ABCDA1 B1C1 D1 равен 105. Найдите объем пирамиды
B1 ABCD .
B1
D1
А1
Ответ: __________
C1
B
А
C
D
14 Найдите значение выражения (1152 − 1032 ) : 208 .
Ответ: __________
15 После снижения цены на 20% спортивный костюм стал стоить 1760 рублей. Сколько рублей
он стоил до понижения?
Ответ: __________
16 Найдите cos α , если sin α =
3
π
и α ∈ ; π .
2
2
Ответ: __________
17 Найдите корень уравнения log 7 (2 x − 3) =
3log 7 2 .
Ответ: __________
18 Каждому из четырёх чисел в левом столбце соответствует промежуток, которому оно принадлежит.
Установите соответствие между числами и промежутками из правого столбца.
Числа
Промежутки
А) log8 9
1) (1; 2)
30
7
В) 7
2) (2; 3)
Б)
Г) 0,33−1
3) (3; 4)
4) (4; 5)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите трёхзначное число, которое при делении на 3 и на 5 даёт в остатке 1, а при делении
на 17 даёт в остатке 8. В ответе укажите какое-нибудь одно такое число..
Ответ: __________
231
20 Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 36 км, затратив на
весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 4
км/ч. Ответ дайте в км/ч
Ответ: __________
21 Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на игровые пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определён
жребием. Всего в турнире участвовало 32 игрока. Сколько было сыграно игр?
Ответ: __________
!
232
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 27
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Каждый день кондитерский магазин продаёт 27 кг конфет «Кара-Кум», которые закупает коробками по 8 кг. На сколько дней хватит 40 коробок?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) длительность драматического спектакля
Б) масса колибри
В) высота собаки в холке
Г) площадь футбольного поля
ЗНАЧЕНИЯ
1) 1,7 г
2) 60 см
3) 2,5 часа
4) 7140 м2
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показана среднемесячная температура воздуха в городе N за каждый месяц года.
По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия.
24
20
16
12
8
4
0 январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
–4
Определите по приведённой диаграмме наименьшую среднемесячную температуру в весенние
месяцы года. Ответ дайте в градусах Цельсия.
Ответ: __________
4
Тело брошено вертикально вверх с высоты 11,2 метра. Пока тело не упало, высота, на которой
оно находится, описывается формулой h(t ) = 11, 2 + 10t − 5t 2 , где h – высота в метрах, t – время
в секундах, прошедшее с момента броска. На какой высоте будет тело через 2 секунды?
Ответ: __________
233
5
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле
равна 0,7. Найдите вероятность того, что он промахнулся ровно один раз.
Ответ: __________
6
Для изготовления шкафов требуется заказать 70 одинаковых зеркал в одной из трёх фирм.
Площадь каждого зеркала 0,3 м2. В таблице приведены цены на зеркала, а также на резку зеркал
и шлифовку края. Сколько рублей будет стоить самый дешёвый заказ?
Фирма
Цена зеркала
(рублей за 1 м2)
Резка и шлифовка
(рублей за одно зеркало)
А
900
150
Б
850
160
В
950
140
Ответ: __________
7
Установите соответствие между функциями и характеристиками этих функций на отрезке [1; 5] .
ФУНКЦИЯ
ХАРАКТЕРИСТИКА
А) f ( x) = x 2 + 3 x + 5
1) функция убывает на всём отрезке [1; 5]
Б)
2) функция возрастает на всём отрезке [1; 5]
2
f ( x) =
− x − 5x + 1
3) функция имеет точку максимума на отрезке [1; 5]
В) f ( x) = x 2 − 5 x + 3
4) функция имеет точку минимума на отрезке [1; 5]
Г) f ( x) =
− x 2 + 3x + 7
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
Для поступления в медицинский институт необходимо сдать экзамен по биологии или химии.
Выберите утверждения, которые верны при указанных условиях.
1) Если человек не поступил в медицинский институт, то он не сдал экзамен ни по химии,
ни по биологии.
2) Если человек поступил в медицинский институт, то он сдал экзамен по химии и биологии.
3) Всякий человек, сдавший экзамен по химии или биологии, может поступить в медицинский
институт.
4) Если человек не сдал экзамен ни по химии, ни по биологии, то он не поступил в медицинский институт.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
234
9
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на
местности). Оцените, скольким квадратным километрам равна площадь озера «Круглое»
изображённого на плане. Ответ округлите до целого числа.
Заповедник
Оз. Круглое
Оз. Малое
Ответ: __________
10
Человек, стоящий между фонарем, высота которого равна 6,5 м, и вертикальной стеной,
отбрасывает на стену тень высотой 50 см. Найдите рост человека, если расстояние от него до
фонаря равно 3 м, а до стены – 1 м. Ответ выразите в сантиметрах.
Ответ: __________
11 Однородный цилиндр с радиусом основания 3 см и высотой 8 см весит
504 г. Сколько весит цилиндр с радиусом основания 2 см и высотой
6 см, изготовленный из того же материала. Ответ выразите в граммах.
Ответ: __________
12 Стороны параллелограмма равны 13 и 10. Высота, опущенная на большую сторону, равна 7. Найдите высоту, опущенную на меньшую сторону параллелограмма.
Ответ: __________
13
Объем куба ABCDA1 B1C1 D1 равен 144. Найдите объем пирамиды
OABC , где точка O – центр грани CC1 D1 D .
Ответ: __________
14 Найдите значение выражения (1232 − 1052 ) : 228 .
Ответ: __________
235
15 После повышения цены на 25% куртка стала стоить 7000 рублей. Сколько рублей она стоила
до повышения?
Ответ: __________
16 Найдите sin α , если cos α = −
3
π
и α ∈ ; π .
2
2
Ответ: __________
17 Найдите корень уравнения log3 (24 − 3 x) =
2log3 3 .
Ответ: __________
18 Каждому из четырёх чисел в левом столбце соответствует промежуток, которому оно принадлежит. Установите соответствие между числами и промежутками из правого столбца.
ЧИСЛА
ПРОМЕЖУТКИ
А) log 4 104
1) (3; 4)
39
9
В) 40
2) (4; 5)
Б)
Г) 0,19−1
3) (5; 6)
4) (6; 7)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите трёхзначное число, которое при делении на 3 и на 11 даёт в остатке 1, а при делении
на 7 даёт в остатке 3. В ответе укажите какое-нибудь одно такое число.
Ответ: __________
20 Баржа прошла по течению реки 45 км и, повернув обратно, прошла ещё 42 км, затратив на весь
путь 6 часов. Найдите собственную скорость баржи, если скорость течения реки равна 3 км/ч.
Ответ: __________
21 Турнир по настольному теннису проводится по олимпийской системе в несколько туров: если
в туре участвует чётное число игроков, то они разбиваются на случайные игровые пары. Если
число игроков нечётно, то с помощью жребия выбираются случайные игровые пары, а один
игрок остаётся без пары и не участвует в туре. Проигравший в каждой паре (ничья невозможна)
выбывает из турнира, а победители и игрок без пары, если он есть, выходят в следующий тур,
236
который проводится по таким же правилам. Так продолжается до тех пор, пока не останутся
двое, которые играют между собой финальный тур, то есть последнюю партию, которая выявляет
победителя турнира. В турнире участвовало 17 игроков. Сколько было сыграно игр?
Ответ: __________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
237
ВАРИАНТ № 28
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Каждый день кофейня расходует 11 литров молока, которое закупает пакетами по 1,9 литра. На
сколько дней хватит 200 пакетов молока?
Ответ: __________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) масса телевизора
Б) высота футбольных ворот
В) время оборота Венеры вокруг солнца
Г) площадь тетрадного листа
ЗНАЧЕНИЯ
1) 338 см2
2) 243 суток
3) 2,44 м
4) 7 кг
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показана среднемесячная температура воздуха в городе N за каждый месяц года.
По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия.
24
20
16
12
8
4
0 январь февраль март
апрель
май
июнь
июль
август сентябрь октябрь ноябрь декабрь
–4
Определите по приведённой диаграмме наименьшую среднемесячную температуру в летние
месяцы года. Ответ дайте в градусах Цельсия.
Ответ: __________
4
Тело брошено под углом к горизонту с высоты 3,6 метра. Пока тело не упало, высота, на которой
оно находится, описывается формулой h(t ) = 3,6 + 8t − 5t 2 , где h – высота в метрах, t – время
в секундах, прошедшее с момента броска. На какой высоте будет тело через 0,4 секунды?
Ответ: __________
238
5
Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле
равна 0,6. Найдите вероятность того, что он попал в мишень ровно один раз.
Ответ: __________
6
Для изготовления шкафов требуется заказать 75 одинаковых зеркал в одной из трёх фирм.
Площадь каждого зеркала 0,4 м2. В таблице приведены цены на зеркала, а также на резку зеркал
и шлифовку края. Сколько рублей будет стоить самый дешёвый заказ?
Фирма
Ценя зеркала
(рублей за 1 м2)
Резка и шлифовка
(рублей за одно зеркало)
А
650
140
Б
700
130
В
750
120
Ответ: __________
7
Установите соответствие между функциями и характеристиками этих функций на отрезке [1; 5] .
ФУНКЦИЯ
ХАРАКТЕРИСТИКА
А) f ( x) = x 2 + 7 x + 5
1) функция убывает на всём отрезке [1; 5] .
Б) f ( x) = x 2 + 4 x + 1
2) функция возрастает на всём отрезке [1; 5] .
В) f ( x) =
− x − 8x + 3
3) функция имеет точку максимума на отрезке [1; 5] .
Г) f ( x) =
− x 2 − 3x + 7
4) функция имеет точку минимума на отрезке [1; 5] .
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
Любой ученик, получивший оценку «5» за полугодие по истории, писал реферат или делал доклад. Выберите утверждения, которые верны при указанных условиях.
1)
2)
3)
4)
Если ученик написал реферат, то он получил «5» за полугодие.
Если ученик не писал реферат и не делал доклад, то он не получил «5» за полугодие.
Если ученик не получил «5» за полугодие, то он не писал реферат и не делал доклад.
Всякий ученик, написавший реферат и сделавший доклад, получил «5» за полугодие.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: __________
239
9
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на
местности). Оцените, скольким квадратным километрам равна площадь озера «Большое»,
изображённого на плане. Ответ округлите до целого числа.
Оз. Малое
Заповедник
Оз. Большое
Ответ: __________
10
Между фонарем, высота которого равна 8 м, и вертикальной стеной стоит человек ростом
1,6 м. Найдите высоту тени, отбрасываемой человеком на стену, если расстояние от него до
фонаря равно 5 м, а до стены – 1 м. Ответ выразите в сантиметрах.
Ответ: __________
11 Однородный цилиндр с радиусом основания 5 см и высотой 7 см весит
1400 г. Сколько весит цилиндр с радиусом основания 3 см и высотой
4 см, изготовленный из того же материала. Ответ выразите в граммах.
Ответ: __________
12 Стороны параллелограмма равны 7 и 25. Высота, опущенная на меньшую сторону, равна 15. Найдите высоту, опущенную на большую сторону параллелограмма.
Ответ: __________
B1
13 Объем куба ABCDA1 B1C1 D1 равен 48. Найдите объем пирамиды OABCD ,
где точка O – центр грани A1 B1C1 D1 .
А1
Ответ: __________
D1
B
А
240
C1
O
C
D
14 Найдите значение выражения (137 2 − 1192 ) :18 .
Ответ: __________
15 После снижения цены на 30% кроссовки стали стоить 3010 рублей. Сколько рублей они стоили
до понижения?
Ответ: __________
3π
π 3π
16 Найдите sin − α , если sin α = −0,6 и α ∈ ; .
2
2 2
Ответ: __________
17 Найдите корень уравнения log11 ( x − 2) =
4log11 5 .
Ответ: __________
18 Каждому из четырёх чисел в левом столбце соответствует промежуток, которому оно принадлежит. Установите соответствие между числами и промежутками из правого столбца..
ЧИСЛА
А) log 2 13
50
Б)
11
В)
31
Г) 0,35−1
ПРОМЕЖУТКИ
1) (2; 3)
2) (3; 4)
3) (4; 5)
4) (5; 6)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Найдите трёхзначное число, которое при делении на 5 и на 7 даёт в остатке 1, а при делении
на 11 даёт в остатке 6. В ответе укажите какое-нибудь одно такое число.
Ответ: __________
20 Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив
на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в
неподвижной воде, если скорость течения реки равна 4 км/ч.
Ответ: __________
241
21 Турнир по настольному теннису проводится по олимпийской системе в несколько туров: если
в туре участвует чётное число игроков, то они разбиваются на случайные игровые пары. Если
число игроков нечётно, то с помощью жребия выбираются случайные игровые пары, а один
игрок остаётся без пары и не участвует в туре. Проигравший в каждой паре (ничья невозможна)
выбывает из турнира, а победители и игрок без пары, если он есть, выходят в следующий тур,
который проводится по таким же правилам. Так продолжается до тех пор, пока не останутся
двое, которые играют между собой финальный тур, то есть последнюю партию, которая выявляет
победителя турнира. В турнире участвовало 40 игроков. Сколько было сыграно игр?
Ответ: __________
!
242
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ВАРИАНТ № 29
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Сколько банок краски необходимо купить для покраски поверхности площадью 20 м2, если
расход краски составляет 600 г/м2, а масса краски в одной банке 1,6 кг?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями: к каждому элементу
первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) площадь игровой комнаты
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 8,51 км2
Б) площадь стандартного тетрадного листа
2) 900 мм2
В) площадь почтовой марки
3) 338,25 см2
Г) площадь озера Сенеж в Московской области
4) 50 м2
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
Б
В
Г
На диаграмме показаны результаты тестирования учащихся. Тест состоял из 22 заданий. Каждый
столбец диаграммы показывает, сколько процентов от общего числа проходивших тестирование
составляют участники, верно решившие соответствующее число заданий. По вертикали указана
доля учащихся, верно решивших соответствующие число заданий, в процентах от общего числа проходивших тестирование, а по горизонтали – количество верно решённых заданий теста.
Учащиеся, верно решившие менее 8 заданий, тест не сдали.
12
10
Доля решивших (в %)
3
А
10,2
9,3
9,1
7,6
8
5,7
6
5,4
5,9
7,9
7,4
5,4
5,9
4,5
4
3,1
2
2
0,3
0
3,4
2,5
2,5
0,8 0,8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Количество верных ответов
Определите по диаграмме суммарный процент учащихся, не сдавших тестирование.
Ответ: ___________
243
4
Используя формулу для вычисления потенциальной энергии тела (в джоулях) E = mgh , где
m – масса тела (в килограммах), g = 9,8 – ускорение свободного падения в (м/c2), h – высота
(в метрах), на которой находится тело, относительно поверхности, найдите m (в килограммах),
если h = 20 м, а E = 392 Дж.
Ответ: ___________
5
Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 3. Результат округлите до десятых.
Ответ: ___________
6
Три фирмы предлагают услуги по грузоперевозкам. Стоимость услуг, предоставляемых фирмами, приведены в таблице. Необходимо перевезти 35 тонн груза на 800 км. Сколько рублей
нужно заплатить за самую дешёвую перевозку в одной из этих фирм?
Номер
фирмы
1
Стоимость перевозки одним
грузовиком (руб. на 100 км)
4000
Грузоподъёмность одного
грузовика (тонны)
6
2
4500
8
3
5800
10
Ответ: ___________
7
На рисунке изображены графики функций вида y = ax 2 + bx + c . Установите соответствие между
графиками этих функций и их точками экстремума (максимума или минимума).
Графики
А)
Б)
В)
Г)
y
y
y
y
1
1
1
1
0 1
0 1
0 1
x
x
x
0 1
x
Точки экстремума:
1) xmax = 4
2) xmin = −1
3) xmax = −2
4) xmin = 3
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
244
А
Б
В
Г
В классе 20 учеников. Из них 15 занимаются в секции легкой атлетики, а 10 по выходным посещают бассейн. Выберите утверждения, которые верны при указанных условиях.
1) В этом классе найдётся хотя бы 5 учеников, занимающихся в секции и посещающих бассейн.
2) Найдётся 10 учеников класса, которые не занимаются в секции и не посещают бассейн.
3) Не более 10 учеников класса занимаются в секции и посещают бассейн.
4) В этом классе не найдётся ни одного ученика, занимающегося только в секции.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 км × 1 км. Найдите
площадь озера Базовое, изображённого на плане. Ответ дайте в квадратных километрах с точностью до целого числа.
Оз. Базовое
1 км
Ответ: ___________
10 Лодочная станция имеет форму равнобедренной трапеции с боковой стороной 30 м и основаниями 38 м и 26 м. Большая сторона трапеции идёт вдоль берега озера, а три остальные стороны
нужно обнести забором. Найдите длину забора. Ответ дайте в метрах.
Ответ: ___________
11
Трубу цилиндрической формы требуется покрасить снаружи. Найдите
площадь окрашиваемой поверхности, если длина трубы 6 м, внешний
обхват трубы составляет 24 см, а торцы красить не надо. Ответ дайте
в квадратных сантиметрах.
Ответ: ___________
12
C
ABCDEFGH – правильный восьмиугольник. Точка O – центр опи-
B
санной около него окружности. Найдите угол BOD . Ответ дайте в
градусах.
Ответ: ___________
A
D
E
O
H
F
G
245
13
Объём конуса равен 72. Плоскость, проходящая через середину высоты
конуса параллельно плоскости основания, отсекла от конуса верхнюю
часть. Найдите объём оставшейся части.
Ответ: ___________
14 Найдите значение выражения 7,35 − 0,005 ⋅ 70 .
14
Ответ: ___________
15 В городе А живет 100 000 жителей. Из них 15% составляют дети и подростки. Среди взрослых
жителей 30% не работают по разным причинам. Сколько взрослых в городе не работают?
Ответ: ___________
16
Найдите значение выражения
(
)
2
13 − 1 − 14
52
.
Ответ: ___________
17
Найдите корень уравнения log 3
x
= −3 .
27
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений из
правого столбца. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
1)
А) log 5 x < 1 ;
Б)
В)
2 x + 10
> 0;
5− x
2)
x+5
> 0;
2 x − 10
3)
Г) 2 x−5 < 1 .
4)
–5
0
–5
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
246
А
Б
В
Г
5
x
5
x
5
x
5
x
19 Шестизначное число оканчивается цифрой 7. Если эту цифру переставить из конца в начало,
не изменяя порядка остальных цифр, то получится число, которое в 5 раз больше исходного.
Найдите исходное число.
Ответ: ___________
20 Автобус проехал 180 км за 2 часа. Во сколько раз должна уменьшиться его скорость, чтобы он
проехал 240 км за 4 часа?
Ответ: ___________
21
Жук за один ход заползает вверх по доске на 4 метра, но скатывается вниз на 1,5 м. За сколько
ходов жук впервые окажется на высоте 8 метров?
Ответ: ___________
!
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
247
ВАРИАНТ № 30
Ответом к каждому заданию является конечная десятичная дробь, или целое число, или последовательность цифр. Ответ сначала запишите в поле ответа в тексте работы, а затем
перенесите в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными
в бланке образцами. Единицы измерений писать не нужно.
1
Сколько банок краски необходимо купить для покраски поверхности площадью 24 м2, если
расход краски составляет 800 г/м2, а масса краски в одной банке 1,7 кг?
Ответ: ___________
2
Установите соответствие между величинами и их возможными значениями. К каждому элементу
первого столбца подберите соответствующий элемент второго столбца.
ЗНАЧЕНИЯ
ВЕЛИЧИНЫ А) Площадь Северного Ледовитого океана
Б) Радиус планеты Венера
В) Масса Луны
Г) Объём воды в озере Онежское
1)
2)
3)
4)
295 км3
6051,8 км
7,35 ⋅ 10²² кг
14,75 ⋅ 106 км2
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
3
А
Б
В
Г
На диаграмме показаны результаты тестирования учащихся. Тест состоял из 22 заданий. Каждый
столбец диаграммы показывает, сколько процентов от общего числа проходивших тестирование
составляют участники, верно решившие соответствующее число заданий. Учащиеся распределены на группы по количеству верно решённых заданий. По вертикали указана доля учащихся,
верно решивших соответствующие число заданий, в процентах от общего числа проходивших
тестирование, а по горизонтали – количество верно решённых заданий теста. Учащиеся верно
решившие более 18 заданий, были отобраны для участия в олимпиаде.
12
Доля решивших (в %)
10
10,2
9,3
9,1
7,6
8
5,7
6
5,4
5,9
7,4
5,4
5,9
4,5
4
3,1
2
2
0,3
0
3,4
2,5
2,5
0,8 0,8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Количество верных ответов
248
7,9
Определите по диаграмме, сколько заданий решили учащиеся в самой многочисленной группе
среди групп учащихся, отобранных на олимпиаду.
Ответ: ___________
4
Используя формулу для вычисления потенциальной энергии тела (в джоулях) E = mgh , где m
– масса тела (в килограммах), g = 9,8 – ускорение свободного падения в (м/c2), h – высота (в
метрах), на которой находится тело, относительно поверхности, найдите Е (в джоулях), если
m = 10 кг, а h = 14 м.
Ответ: ___________
5
Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
Ответ: ___________
6
Три фирмы предлагают услуги по грузоперевозкам. Стоимость услуг, предоставляемых фирмами, приведены в таблице. Необходимо перевезти 35 тонн груза на 800 км. Сколько рублей
нужно заплатить за самую дешёвую перевозку в одной из этих фирм?
Номер фирмы
Стоимость перевозки одним грузовиком
(руб. на 100 км)
Грузоподъёмность одного
грузовика (тонны)
1
4100
6
2
4500
8
3
5400
10
Ответ: ___________
7
На рисунке изображены графики функций вида y = ax 2 + bx + c . Установите соответствие между
графиками этих функций и их точками экстремума (максимума или минимума).
Графики
А)
А)
Б)
Б)
В)
В)
y
y
y
1
0 1
1
x
Г)
Г)
y
1
0 1
0 1
x
1
x
0 1
x
Точки экстремума:
1) xmin = 4
2) xmax = −1
3) xmin = −2
4) xmax = 3
249
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
8
А
Б
В
Г
В классе 22 учеников. Из них 15 занимаются в секции легкой атлетики, а 11 по выходным посещают бассейн. Выберите утверждения, которые верны при указанных условиях.
1)
2)
3)
4)
В этом классе найдётся хотя бы 4 ученика, занимающихся в секции и посещающих бассейн.
Найдётся 11 учеников класса, которые не занимаются в секции и не посещают бассейн.
Не более 11 учеников класса занимаются в секции и посещают бассейн.
В этом классе не найдётся ни одного ученика, занимающегося только в секции.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ___________
9
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 км × 1 км. Найдите
площадь озера Профильное, изображённого на плане. Ответ дайте в квадратных километрах с
точностью до целого числа.
1 км
Оз. Профильное
Ответ: ___________
10 Лодочная станция имеет форму равнобедренной трапеции с боковой стороной 40 м и основаниями 38 м и 34 м. Большее основание трапеции идёт вдоль берега озера, а три остальные
стороны нужно обнести забором. Найдите длину забора. Ответ дайте в метрах.
Ответ: ___________
11
Трубу цилиндрической формы требуется покрасить снаружи. Найдите
площадь окрашиваемой поверхности, если длина трубы 14 м, внешний
обхват трубы составляет 25 см, а торцы красить не надо. Ответ дайте
в квадратных сантиметрах.
Ответ: ___________
250
12
C
ABCDEFGH – правильный восьмиугольник. Точка O – центр описанной около него окружности. Найдите угол GOD. Ответ дайте в
градусах.
Ответ: ___________
B
D
A
E
O
H
F
G
13 Объём конуса равен 80. Плоскость, проходящая через середину высоты конуса, параллельно плоскости основания, отсекла от конуса верхнюю часть.
Найдите объём оставшейся части.
Ответ: ___________
14
8,56 − 0,008 ⋅ 70
.
16
Найдите значение выражения
Ответ: ___________
15
В городе А живет 200 000 жителей. Из них 20% составляют дети и подростки. Среди взрослых жителей 30% не работают по разным причинам.. Сколько взрослых в городе не работают?
Ответ: ___________
16 Найдите значение выражения
(
)
2
15 − 1 − 16
60
.
Ответ: ___________
17
Найдите корень уравнения log 2
x
= −3 .
8
Ответ: ___________
18
Каждому из четырёх неравенств в левом столбце соответствует одно из решений из
правого столбца. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
А) log 4 x < 1 ;
РЕШЕНИЯ
1)
Б)
2x + 8
<0;
4− x
2)
В)
x+4
< 0;
2x − 8
3)
Г) 4 x− 4 < 1 .
4)
–4
0
–4
4
x
4
x
4
x
4
x
251
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
А
Б
В
Г
19 Шестизначное число оканчивается цифрой 4. Если эту цифру переставить из конца числа в
начало, не изменяя порядка остальных цифр, то получится число, которое в 4 раза больше исходного. Найдите исходное число.
Ответ: ___________
20 Автобус проехал 160 км за 2 часа. Сколько километров он проедет за 3 часа, если его скорость
уменьшится в полтора раза?
Ответ: ___________
21 Муравей находится на дне колодца глубиной 30 метров. За день он поднимается на 18 метров,
а за ночь спускается вниз на 15 метров. Сколько дней понадобится муравью для того, чтобы
подняться до верха колодца?
Ответ: ___________
!
252
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ОТВЕТЫ
Глава 1. АЛГЕБРА, НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА,
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СТАТИСТИКА
§ 1. Числа и вычисления
1.1. Дроби
1. а) 19,5; б) 25,1; в) 0,068; г) 33,3; д) 29,74; е) 29. 2. а) 12,3; б) 19,35; в) 8,5; г) 198; д) 31; e) 23,4.
3. а) 2,33; б) 1,1; в) 0,6; г) 3,65. 4. а) 4,5625; б) 12,5; в) −16,191; г) −2,6525. 5. а) 5,5; б) 6,5; в) 1;
г) 3,4; д) 2; е) 2; ж) 2,625; з) 1; и) 1; к) 1,5; л) 4; м) 4. 6. а) 3,625; б) 0,08; в) 0,25; г) 0,05. 7. а) 49,5;
б) 29,9; в) −140; г) −420. 8. а) 2; б) 25; в) 1; г) 6; д) 7; e) 3. 9. а) 1,2; б) 1,5; в) 0,27; г) 0,35. 10. а) 1;
б) 23; в) 132; г) 4,5; д) 9,5. 11. а) −2; б) 4; в) −3; г) 5. 12. а) 0,3; б) 0,9; в) 0,09; г) 0,035. 13. а) –5;
б) −5; в) 1; г) −0,175. 14. а) −4; б) −18; в) −0,98; г) 1. 15. а) 0,25; б) −0,06; в) 0,365; г) 1,85.
Проверочная работа № 1
Вариант 1.
Вариант 2.
1. а) 0,2; б) 4,2; в) 87. 2. а) 0,5; б) 0,75; в) 27; г) 798.
1. а) 1003; б) 4,9; в) 189. 2. а) 4; б) 2,5; в) 1,25; г) 187.
1.2. Степень с целым показателем
16. а) 9; б) 343; в) 0,125; г) 0,008. 17. а) 27; б) 16; в) 0,04; г) 0,0625. 18. а) 1; б) 1; в) 4; г) 6.
19. а) 1; б) 1; в) 0,001; г) 10000. 20. а) 1; б) 1; в) 81; г) 0,0625. 21. а) 537; б) 0,7805; в) 8020,7;
г) 0,04097. 22. а) 288; б) 100; в) 32000; г) 0,0049. 23. а) 58; б) 124600; в) 521; г) −836. 24. а) 1900;
б) 0,075; в) 400; г) −0,011.
Проверочная работа № 2
Вариант 1
Вариант 2
1. а) 36; б) 256; 2. а) 116; б) 0,8612; 3. 0,959.
1. а) 0,04; б) 81; 2. а) 1040; б) 0,13108; 3. −0,9909.
1.3. Иррациональные числа
25. а) 120; б) 160; в) 0,03; г) 0,025; д) 2,9; е) 1,5. 26. а) 1,375; б) 2,25; в) 2,6; г) 8,5. 27. а) 36; б) 30;
в) 6,6; г) 0,3. 28. а) 7,8; б) 22,5; в) 2,9; г) 1,5. 29. а) 108; б) 2000; в) 112; г) 720. 30. а) 11; б) 4; в) 0,6;
г) 0,9. 31. а) 12,5; б) 20,25; в) 0,75; г) 0,08. 32. а) 17; б) 18; в) 1; г) 2,4. 33. а) 8; б) 21; в) 6; г) −50.
34. а) 72; б) 7; в) 345; г) 15.
Проверочная работа № 3
Вариант 1.
Вариант 2.
1. а) 1,2; б) 1,2; в) 60; г) 432. 2. а) 21; б) 2,25. 3. а) 13; б) 32; в) 45.
1. а) 1,4; б) 1,75; в) 42; г) 576. 2. а) 23,4; б) 0,75. 3. а) 15; б) 20; в) 150.
1.4. Логарифмы
35. а) 4; б) 3; в) −3; г) −1; д) 0; е) −5; ж) −2; з) 3. 36. 4. 37. 3. 38. а) 2; б) 2. 39. а) 2; б) 8; в) 0,125;
г) 6; д) −2,5; е) −1,5. 40. а) 1; б) 1; в) −1; г) 2. 41. а) 3; б) 5; в) 3; г) 5. 42. а) 3; б) 2; в) 2; г) −1.
43. а) 3; б) 5; в) 4; г) 0,5. 44. а) 0,04; б) 81; в) 64; г) 3; д) 33; е) 1; ж) 81; з) 125; и) 3; к) 13. 45. а) 1;
б) 1,25; в) 3; г) 2. 46. а) 3; б) 2; в) 4; г) 11,5.
Проверочная работа № 4
Вариант 1.
Вариант 2.
1. а) 3; б) −2; в) 0; г) 0,4; д) 0,5 2. а) 2; б) 1; в) 21; г) 250; д) 16.
1. а) 3; б) −3; в) 0; г) 0,125; д) 0,5. 2. а) 3; б) 4; в) 0,5; г) 243; д) 15.
253
1.5. Тригонометрические выражения
47. а) −1,5; б) −2; в) 4; г) 0; д) −3; е) −10,5; ж) 6; з) 13; и) 0; к) −24; л) −1,5; м) −30. 48. а) 15;
б) 0,25; в) 3; г) −0,125. 49. а) −6; б) −2; в) 151; г) −25. 50. −0,6. 51. 3. 52. −0,28. 53. 6. 54. 5. 55. −0,75.
Проверочная работа № 5
Вариант 1.
Вариант 2.
1. а) −6; б) 0; в) 9; г) −3; д) 21. 2. −2.
1. а) −12; б) −8; в) −12; г) −0,125; д) −13. 2. −5.
1.6. Координатная прямая
56. 3214. 57. 4123. 58. 4312. 59. 1423. 60. 2314. 61. 1243. 62. 3412. 63. 2134. 64. 1234. 65. 2143.
66. 1342. 67. 4213. 68. 4213. 69. 1342. 70. 3421. 71. 4231. 72. 3412.
1.7. Числа и их свойства
73. 13; 31. 74. 27. 75. 15; 24. 76. 23; 35; 47; 59. 77. 532. 78. 917; 973. 79. 307; 317; 327; 337; 347.
80. 102; 112; 122; 132; 142. 81. 1045. 82. 1076. 83. 4987; 6142; 8452; 9607. 84. 4621; 6931; 9241.
85. 1225; 2125. 86. 147; 357; 567; 777; 987. 87. 159; 234; 468; 543; 852. 88. 2406; 2460; 2608; 2680;
2846; 2864. 89. 2310; 4620. 90. 8190; 8610; 9240; 9450; 9870. 91. 14274; 16254; 91674. 92. 35472;
36792; 51792; 54792; 56472.
Проверочная работа № 6
Вариант 1.
Вариант 2.
1. 365. 2. 12122; 12221; 22121.
1. 976. 2. 114144; 141144; 411144.
§ 2. УРАВНЕНИЯ
93. а) −6; б) 4; в) 3; г) −3. 94. а) −2; б) −32; в) 42; г) 20. 95. а) 36; б) 126; в) 20; г) −700. 96. а) 25;
б) 20; в) −11; г) −5. 97. а) 3,4; б) 5; в) 1; г) 1,25 98. а) 4; б) 99; в) −36; г) −195. 99. а) −4; б) 4,5;
в) 1; г) 0,625. 100. а) −1,75; 1,75; б) −0,6; 0,6; в) −0,5; 0,5; г) −0,25; 0,25. 101. а) −1; 1; б) 0; в) −3;
3; г) −2; 2. 102. а) 0; 14; б) 0; 8; в) −62; 0; г) −9; 0; 103. а) 0; 3; б) −3; 0; в) 0; 18; г) −25; 0.
104. а) 0; 0,4; б) 0; 9; в) 0; 1,5; г) 0; 0,125; 105. а) 0; 10; б) −12; 0; в) 0; 2,5; г) 0; 3,5. 106. а) −4;
б) −0,5; в) 6; г) 0,2. 107. а) 1; 6; б) −6; −1; в) −2; 3; г) −3; 2. 108. а) 2; 8; б) −5; −3; в) 6; 8; г) −8; −3.
109. а) −1; 0,6; б) 0,2; 2; в) −0,75; 1; г) −9;1; д) −9; 6; е) −2; 0,4; ж) −6,5; −1; з) −3; 0,2; 110. а) 1; 9;
б) 0,5; 2; в) −1; 16; г) −1,5; 1,4. 111. а) −9; −2; б) −3; 5; в) −3; 1; г) 1,5; 4. 112. а) 0,75; 3; б) −0,2; 7;
в) −0,5; 3; г) −0,625; 2. 113. а) 5; б) 2,6; в) −5,75; г) 5,7. 114. а) 13; б) −25; в) −3; г) −3. 115. а) 11;
б) −3,4; в) 7,25; г) 1. 116. а) 2,5; б) −3; в) −39; г) −44. 117. а) 3; б) −7; в) 2; г) −13; д) 25; е) 169;
ж) 36; з) 196. 118. а) 0; б) 2; в) 1,5; г) 3,75; д) 5; е) 1,25. 119. а) −3,5; б) 0; в) 0,5; г) −1,5. 120. а) 81;
б) 0,125; в) −0,5; г) 40. 121. а) 2; б) 3,5; в) 3,6; г) 6. 122. а) 4,5; б) 10; в) 9; г) 3.
Проверочная работа № 7
Вариант 1
1. а) 1,4; б) 27; в) −1; г) 2. 2. а) −0,5; б) −9; в) 0,25; г) 8; д) 5; е) –5; ж) −4,5. 3. а) 9;
б) 5; в) 1; г) 2,5. 4. а) 6,5; б) −9; в) 0,25; г) 3,125.
1. а) 1,5; б) 54; в) −14,6; г) 1. 2. а) −0,5; б) −7; в) 0,75; г) 7; д) −2; е) 1; ж) 0,375.
Вариант 2
3. а) 8; б) 2; в) 7; г) −2. 4. а) −7,5; б) −0,5; в) 121; г) 3,2.
§ 3. НЕРАВЕНСТВА
123. а)
( −∞; 2] [7; + ∞ ) ;
4
б) − ;1 ; в)
3
254
[ −1,5; 1] ;
б)
г)
( −2; 3) ;
в)
[6; 7] ;
г)
( −∞; − 5) ( 7; + ∞ ) ;
( −∞; − 9 ) ( 3; + ∞ ) .
124. а)
( −∞; 3] [7; + ∞ ) ;
5
1
д) − ; 1 ; е) ∅ ; ж) −∞; − ( 2; + ∞ ) ;
7
9
3
и) − ; 3 ; к) ∅ ; л) ( −∞; − 0, 25 ) (1; + ∞ ) ; м) ( −∞; + ∞ ) . 125. а) [ 0; 2 ) ; б) ( −4; 3] ;
7
в) ( −∞; − 7] ( 5; + ∞ ) ; г) ( 7; 11) ; д) ( −3;12 ) ; е) ( −∞; − 9 ) (13; + ∞ ) ; ж) ( −∞; −15] (14; + ∞ ) ;
з)
( −∞; + ∞ ) ;
з) ( 0;18] . 126. а) ( −3; 1) (1; + ∞ ) ; б) ( −∞; 5] ; в) [ 6; + ∞ ) ; г) ( −2; 0 ) ( 0; + ∞ ) ; д) ( −∞; 0] ; е) ( −4; + ∞ ) ;
ж) [ −7; 5 ) ( 5; + ∞ ) ; з) (11; + ∞ ) ; и)
в) [ −1; + ∞ ) ; г)
( −∞; 4 ) ;
( −∞; − 3) ( −3; 12 ) ;
д) [ 0; + ∞ ) ; е) [5,5; + ∞ ) ; ж)
к)
( −∞; − 2 ) .
( −∞; − 1] ;
з)
127. а) (1; + ∞ ) ; б)
( −0,5; + ∞ ) .
128. а)
( −∞; 0] ;
( 4; + ∞ ) ;
б) ( 0; 3] ; в) [ 0,5; + ∞ ) ; г) ( 0; 16 ) ; д) ( −3; − 1] ; е) [ 4, 2; + ∞ ) ; ж) [1; + ∞ ) ; з) ( 2; 3) ; и) ( 0; 1) ; к) (1; + ∞ ) ;
л) ( −1; − 0,99] ; м) [ 2,3; + ∞ ) . 129. 4321. 130. 1243. 131. 4321. 132. 3124. 133. 3241. 134. 4213.
135. 2431. 136. 2413.
Проверочная работа № 8
Вариант 1.
Вариант 2.
2341
1243
§ 4. ТЕКСТОВЫЕ ЗАДАЧИ
4.1. Размеры и единицы измерения
137. 4213. 138. 1342. 139. 2134. 140. 2143. 141. 4321. 142. 3142. 143. 3412. 144. 4231. 145. 4321.
146. 3412. 147. 3421. 148. 4321. 149. 3412. 150. 1324.
4.2. Формулы
151. а) 31; б) 460. 152. а) 55; б) 59. 153. а) 2; б) 1125. 154. а) 40; б) 100. 155. а) 36; б) 2. 156. а) 45;
б) 15. 157. а) 21; б) 42. 158. а) 3; б) 343. 159. а) 48; б) 9. 160. а) 72800; б) 128000. 161. а) 10; б) 12.
162. а) 52; б) 7. 163. а) 90; б) 6. 164. а) 40; б) 36. 165. а) 84; б) 288. 166. а) 8; б) 20. 167. а) 2025;
б) 36100. 168. а) 4650; б) 3700. 169. а) 6000; б) 7500. 170. а) 500; б) 600.
Проверочная работа № 9
Вариант 1.
1. 0,5. 2. 3,75. 3. 8. 4. 1,97. 5. 3.
Вариант 2.
1. 32. 2. 3. 3. 10,2. 4. 2. 5. 5.
4.3. Простейшие текстовые задачи (округление)
171. а) 11; б) 6. 172. а) 23; б) 32. 173. а) 40; б) 25. 174. а) 17; б) 23. 175. а) 54; б) 42. 176. а) 11;
б) 14. 177. а) 9; б) 10. 178. а) 370; б) 560. 179. а) 175; б) 55. 180. а) 140400; б) 219000. 181. а) 78;
б) 222. 182. а) 7; б) 7. 183. а) 8; б) 13. 184. а) 34020; б) 57420. 185. а) 93; б) 100. 186. а) 30; б) 45.
187. а) 19,8; б) 7,5. 188. а) 105; б) 120. 189. а) 9; б) 7. 190. а) 264; б) 387. 191. а) 7320; б) 4575.
192. а) 35; б) 42,5. 193. а) 10; б) 18. 194. а) 11; б) 9. 195. а) 4,8; б) 16. 196. а) 12,5; б) 27.
Проверочная работа № 10
Вариант 1.
1. 69. 2. 276. 3. 25,6. 4. 5.
Вариант 2.
1. 76. 2. 806. 3. 115. 4. 17,5.
255
4.4. Простейшие текстовые задачи (части)
197. а) 65; б) 70. 198. а) 4; б) 3. 199. а) 72; б) 55. 200. а) 20; б) 35. 201. а) 45; б) 56. 202. а) 1200;
б) 540. 203. а) 96; б) 119. 204. а) 3; б) 60. 205. а) 119; б) 156. 206. а) 1755; б) 4760. 207. а) 477;
б) 364. 208. а) 16650; б) 18530. 209. а) 20,4; б) 18. 210. а) 25; б) 40. 211. а) 5100; б) 8000. 212. а) 145;
б) 150. 213. а) 5; б) 8. 214. а) 60; б) 80. 215. а) 1932; б) 2496. 216. а) 840; б) 1156. 217. а) 200; б) 425.
218. а) 7000; б) 8500. 219. а) 80; б) 300. 220. а) 120; б) 35. 221. а) 20; б) 44.
Проверочная работа № 11
Вариант 1.
1. 52. 2. 117,8. 3. 375. 4. 60.
Вариант 2.
1. 46. 2. 284,8. 3. 175. 4. 30.
4.5. Выбор оптимального варианта
222. 72998. 223. 145. 224. 35. 225. 6750. 226. 3024. 227. 8360. 228. 195000. 229. 135; 256. 230. 7488.
231. 10650. 232. 2. 233. 1375000. 234. 15. 235. 9900. 236. 57190. 237. 5925. 238. 2600.
Проверочная работа № 12
Вариант 1.
172000.
Вариант 2.
1612000.
4.6. Текстовые задачи (движение, работа, растворы)
239. а) 8; б) 5. 240. а) 90; б) 36. 241. а) 2; б) 100. 242. а) 89; б) 102. 243. а) 70; б) 60. 244. а) 72;
б) 96. 245. а) 2; б) 180. 246. а) 48; б) 50. 247. а) 11; б) 16. 248. а) 650; б) 625. 249. а) 360; б) 390.
250. а) 600; б) 900. 251. а) 15; б) 18. 252. а) 15; б) 16. 253. а) 12; б) 18. 254. а) 24; б) 15. 255. а) 3:1;
б) 4:1. 256. а) 66; б) 55. 257. а) 67,5; б) 89,6. 258. а) 67,5; б) 90. 259. а) 2,4; б) 12. 260. а) 12; б) 27.
261. а) 13; б) 18. 262. а) 8; б) 12. 263. а) 24; б) 10,5. 264. а) 30; б) 6. 265. а) 60; б) 13. 266. а) 8;
б) 14,4. 267. а) 8; б) 12. 268. а) 54; б) 72. 269. а) 8; б) 19. 270. а) 25; б) 20. 271. а) 17,5; б) 16.
272. а) 4:1; б) 3:2.
Проверочная работа № 13
Вариант 1.
Вариант 2.
1. 1,6. 2. 81. 3. 18. 4. 450. 5. 10.
1. 1. 2. 87,5. 3. 19. 4. 540. 5. 11.
4.7. Анализ утверждений
273. 14. 274. 24. 275. 14. 276. 34. 277. 23. 278. 124. 279. 24. 280. 24. 281. 23. 282. 13. 283. 234.
284. 34. 285. 3. 286. 23. 287. 24. 288. 23. 289. 12.
Проверочная работа № 14
Вариант 1.
Вариант 2.
24
24
4.8. Задачи на смекалку
290. 35. 291. 20. 292. 45. 293. 50. 294. 24. 295. 2. 296. 11. 297. 7. 298. 13. 299. 59. 300. 34. 301. 10.
302. 13. 303. 0. 304. 3. 305. 66. 306. 66. 307. 10. 308. 30. 309. 60. 310. 11. 311. 32. 312. 23. 313. 20.
314. 330. 315. 450.
256
§ 5. АНАЛИЗ ДИАГРАММ И ГРАФИКОВ
316. 2000. 317. 2,7. 318. 5. 319. 6. 320. 3. 321. −6. 322. 9. 323. 29. 324. 13. 325. 11. 326. 20. 327. 65.
328. −21. 329. 15. 330. 15. 331. 3456. 332. 1324. 333. 4312. 334. 4231. 335. 1423. 336. 1432. 337. 4321.
338. 3214. 339. 1423. 340. 1243. 341. 1324. 342. 4312. 343. 1432. 344. 3124. 345. 3241. 346. 4231.
347. 4123. 348. 2143. 349. 2143. 350. 2143. 351. 3241. 352. 3214. 353. 4123. 354. 2143.
Проверочная работа № 15
Вариант 1.
Вариант 2.
1. 1,4. 2. 3421.
1. 2,5. 2. 1342.
§ 6. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
355. а) 0,625; б) 0,15. 356. а) 0,6; б) 0,28. 357. а) 0,6; б) 0,125. 358. а) 0,6; б) 0,4. 359. а) 0,25; б)
0,5; в) 0,8; г) 0,75. 360. а) 0,2; б) 0,35. 361. а) 0,375; б) 0,25. 362. а) 0,98; б) 0,95; в) 0,986; г) 0,95.
363. а) 0,25; б) 0,275. 364. а) 0,27; б) 0,19. 365. а) 0,1; б) 0,8. 366. а) 0,93; б) 0,81. 367. а) 0,2; б) 0,25;
в) 0,1; г) 0,02. 368. а) 0,25; б) 0,75; в) 0,25; г) 0,875; д) 0,375. 369. а) 0,5; б) 0,25; в) 0,75; г) 0,25;
д) 0,17; е) 0,28. 370. а) 0,5; б) 0,5. 371. а) 0,4; б) 0,2; в) 0,6; г) 0,2. 372. а) 0,3; б) 0,3. 373. а) 0,33; б) 0,17.
374. а) 0,039; б) 0,021. 375. а) 0,054; б) 0,013. 376. 0,25. 377. а) 0,14; б) 0,23. 378. а) 0,49; б) 0,36.
379. а) 0,48; б) 0,53. 380. а) 0,096; б) 0,1029; в) 0,02048; г) 0,08. 381. а) 0,2; б) 0,75. 382. а) 0,64;
б) 0,19; в) 0,91; г) 0,2256.
Проверочная работа № 16
Вариант 1
Вариант 2
1. 0,25. 2. 0,8. 3. 0,56. 4. 0,4. 5. 0,56. 6. 0,2.
1. 0,55. 2. 0,96. 3. 0,4. 4. 0,25. 5. 0,8. 6. 0,2.
ГЛАВА 2. ГЕОМЕТРИЯ
§ 7. ПЛАНИМЕТРИЯ
7.1. Прикладные задачи по планиметрии
383. а) 110; б) 1400. 384. а) 15; б) 12. 385. а) 139; б) 95. 386. а) 197; б) 97. 387. а) 12; б) 16.
388. а) 1000; б) 1136. 389. а) 0,01; б) 0,78. 390. а) 6400; б) 6000. 391. а) 13; б) 12. 392. а) 15; б) 24.
393. а) 1,5; б) 2,5. 394. а) 2; б) 1,5. 395. а) 1,2; б) 4. 396. а) 150; б) 30. 397. а) 12; б) 8.
Проверочная работа № 17
Вариант 1.
Вариант 2.
1. 140. 2. 17. 3. 60. 4. 1728. 5. 15000.
1. 220. 2. 9. 3. 24. 4. 768. 5. 680.
398. а) 17,5; б) 12,5; в) 10; г) 13,5. 399. а) 21; б) 8; в) 16; г) 25. 400. а) 6; б) 12; в) 20; г) 12.
401. а) 27,5; б) 22; в) 21; г) 42. 402. а) 12,5; б) 15,5; в) 18; г) 14,5. 403. а) 12; б) 16; в) 15; г) 15.
404. 2. 405. 3. 406. 3. 407. 2.
Проверочная работа № 18
Вариант 1.
1. а) 8; б) 15; в) 22,5; г) 8,5. 2. 3.
Вариант 2.
1. а) 7,5; б) 18; в) 24; г) 17,5. 2. 3.
257
7.2. Углы и длины
408. а) 42; б) 68. 409. а) 80; б) 43. 410. а) 20; б) 63. 411. а) 130; б) 124. 412. а) 47; б) 150.
413. а) 108; б) 136. 414. а) 50; б) 85. 415. а) 86; б) 13. 416. а) 55; б) 35. 417. а) 80; б) 20. 418. а) 28; б) 87,5.
419. а) 76; б) 144. 420. а) 92; б) 58. 421. а) 63; б) 20. 422. а) 114; б) 68; в) 124; г) 48; д) 80; е) 145.
423. а) 78; б) 146; в) 30; г) 106. 424. а) 75; б) 60. 425. а) 135; б) 144. 426. а) 0,5; б) 0,8; в) 1; г) 0,75.
427. а) 20; б) 25. 428. а) 26; б) 7. 429. а) 6; б) 8. 430. а) 9; б) 10. 431. а) 0,28; б) 0,6. 432. а) 128;
б) 14. 433. а) 2; б) 6. 434. а) 3,2; б) 3,6. 435. а) 12; б) 9. 436. а) 20; б) 35. 437. а) 15; б) 10.
438. а) 30; б) 45. 439. а) 2,5; б) 0,5. 440. а) 36; б) 64. 441. а) 6; б) 7. 442. а) 0,25; б) 0,5625. 443. а) 3,5; б) 7.
444. а) 7; б) 5. 445. а) 12; б) 12. 446. а) 51; б) 56. 447. а) 10; б) 25. 448. а) 7,5; б) 2,5. 449. а) 10; б) 9,5.
450. а) 14,4; б) 13,44. 451. а) 3; б) 6. 452. а) 96; б) 24. 453. а) 10; б) 16. 454. а) 18; б) 19,5. 455. а) 3;
б) 5. 456. а) 6; б) 10. 457. а) 24; б) 10. 458. а) 13; б) 84. 459. а) 9; б) 8. 460. а) 5; б) 85. 461. а) 15; б) 3.
Проверочная работа № 19
Вариант 1
Вариант 2
1. 68. 2. 67. 3. 112. 4. 20. 5. 16. 6. 144. 7. 5. 8. 10.
1. 36. 2. 120. 3. 44. 4. −0,2. 5. 6. 6. 56. 7. 12. 8. 15.
7.3. Площади
462. а) 60; б) 34. 463. а) 60; б) 30. 464. а) 48; б) 168. 465. а) 45; б) 30. 466. а) 84; б) 126.
467. а) 31; б) 92. 468. а) 57; б) 112. 469. а) 240; б) 1320. 470. а) 4; б) 12. 471. а) 12; б) 6. 472. а) 5; б) 8.
473. а) 2940; б) 2028. 474. а) 3168; б) 3240. 475. а) 9; б) 8. 476. а) 42; б) 96. 477. а) 32; б) 8.
478. а) 120; б) 64. 479. а) 18; б) 91. 480. а) 70; б) 30. 481. а) 23; б) 12. 482. а) 31; б) 40.
Проверочная работа № 20
Вариант 1
Вариант 2
1. 120. 2. 33. 3. 50. 4. 10,5. 5. 10. 6. 32. 7. 276. 8. 72.
1. 15. 2. 24. 3. 60. 4. 5. 5. 40,5. 6. 20. 7. 528. 8. 92.
7.3. Окружность
483. а) 47; б) 78. 484. а) 66; б) 31. 485. а) 85; б) 75; в) 27; г) 52. 486. а) 140; б) 53. 487. а) 45; б) 146.
488. а) 200; б) 110. 489. а) 60; б) 10. 490. а) 160; б) 3. 491. а) 135; б) 52. 492. а) 8; б) 76. 493. а) 68;
б) 36. 494. а) 10; б) 75. 495. а) 54; б) 38. 496. а) 17,5; б) 19,5. 497. а) 121; б) 93. 498. а) 79; б) 57.
499. а) 10; б) 12. 500. а) 13; б) 16. 501. а) 135; б) 45; в) 22,5; г) 45; д) 90; е) 90.
Проверочная работа № 21
Вариант 1
Вариант 2
1. 78. 2. 57. 3. 62. 4. 260. 5. 144. 6. 16.
1. 150. 2. 30. 3. 126. 4. 6. 5. 48. 6. 6.
§ 8. СТЕРЕОМЕТРИЯ
8.1. Прикладные задачи по стереометрии
502. а) 18; б) 27; в) 11. 503. а) 24; б) 36; в) 14. 504. а) 10; б) 15; в) 7. 505. а) 8; б) 12; в) 6. 506. а) 6;
б) 9; в) 5. 507. а) 8000; б) 12500. 508. а) 94,5; б) 140. 509. а) 3; б) 8. 510. а) 86; б) 56; в) 72; г) 84.
511. а) 44; б) 20; в) 32; г) 28. 512. а) 31,5; б) 99. 513. а) 11250; б) 5400. 514. а) 16; б) 140. 515. а) 9600;
б) 12600. 516. а) 18000; б) 74400. 517. а) 8; б) 6,75. 518. а) 128; б) 54. 519. а) 375; б) 375.
258
Проверочная работа № 22
Вариант 1.
Вариант 2.
1. 45. 2. 154. 3. 13,5.
1. 17. 2. 308. 3. 32.
8.2. Задачи по стереометрии
520. а) 7; б) 11. 521. а) 10; б) 30. 522. а) 96; б) 150. 523. а) 96; б) 216. 524. а) 366; б) 384.
525. а) 96; б) 630. 526. а) 192; б) 140. 527. а) 195; б) 765. 528. а) 8; б) 8. 529. а) 900; б) 144.
530. а) 128; б) 288. 531. а) 240; б) 390. 532. а) 1350; б) 336. 533. а) 112,5; б) 180. 534. а) 5; б) 4. 535. а) 4; б) 4.
536. а) 5; б) 3. 537. а) 17; б) 13. 538. а) 72; б) 40. 539. а) 12; б) 5. 540. а) 144; б) 216. 541. а) 480; б) 672.
542. а) 360; б) 1008. 543. а) 4; б) 5,5. 544. а) 2; б) 3. 545. а) 12; б) 16. 546. а) 28; б) 25. 547. а) 70;
б) 100. 548. а) 9; б) 6,75. 549. а) 24; б) 12. 550. а) 18; б) 32. 551. а) 112; б) 80. 552. а) 12,5; б) 4.
553. а) 5; б) 3. 554. а) 34; б) 192. 555. а) 192; б) 72. 556. а) 12,5; б) 4. 557. а) 7; б) 3. 558. а) 10; б) 3.
559. а) 27; б) 54. 560. а) 27; б) 64. 561. а) 4; б) 25.
Проверочная работа № 23
Вариант 1.
Вариант 2.
1. 120. 2. 600. 3. 60. 4. 5.
1. 180. 2. 252. 3. 128. 4. 5.
ГЛАВА 3. ТРЕНИРОВОЧНЫЕ ВАРИАНТЫ
Вариант № 1
1. 406,4. 2. 2431. 3. 18. 4. 85. 5. 0,1. 6. 8498. 7. 2134. 8. 24. 9. 18. 10. 120. 11. 4. 12. 68. 13. 3. 14. 125.
15. 12,5. 16. 11. 17. 1,5. 18. 2413. 19. 167; 497; 827. 20. 1,6. 21. 52.
Вариант № 2
1. 355,6. 2. 3142. 3. −6. 4. 97. 5. 0,3. 6. 21305. 7. 2341. 8. 34. 9. 16. 10. 105. 11. 3. 12. 76. 13. 7.
14. 0,64. 15. 20. 16. −42. 17. 1. 18. 4231. 19. 183; 365; 547; 729. 20. 1. 21. 18.
Вариант № 3
1. 27. 2. 2143. 3. −21. 4. 12,5. 5. 0,12. 6. 10965. 7. 4231. 8. 14. 9. 12,5. 10. 5. 11. 297. 12. 119. 13. 144.
14. 27,2. 15. 102. 16. −50. 17. 25. 18. 4213. 19. 3528; 3564; 3672; 3708; 3780. 20. 81. 21. 480.
Вариант № 4
1. 16. 2. 1423. 3. 21. 4. 3. 5. 0,1. 6. 12076. 7. 3142. 8. 23. 9. 16,5. 10. 10. 11. 24. 12. 119. 13. 576.
14. 7,9. 15. 140. 16. 21. 17. −39. 18. 3124. 19. 3975. 20. 87,5. 21. 154.
Вариант № 5
1. 1798. 2. 3142. 3. 387,5. 4. 39,5. 5. 0,875. 6. 171600. 7. 1423. 8. 13. 9. 14,5. 10. 2. 11. 18. 12. 53.
13. 300. 14. 5,2. 15. 90000. 16. 0,0625. 17. 1. 18. 2314. 19. 2976. 20. 18. 21. 12.
Вариант № 6
1. 1906. 2. 3241. 3. 392,5. 4. 30,5. 5. 0,04. 6. 299342,4. 7. 2314. 8. 12. 9. 14,5. 10. 3. 11. 10. 12. 140.
13. 30. 14. 7,6. 15. 120000. 16. 81. 17. −5. 18. 3421. 19. 4320; 4032. 20. 19. 21. 9.
Вариант № 7
1. 2070. 2. 4123. 3. 200. 4. 212,5. 5. 0,25. 6. 64. 7. 4321. 8. 2. 9. 26. 10. 1400. 11. 20. 12. 55. 13. 15.
14. 5. 15. 3255. 16. 210. 17. 3. 18. 3124. 19. 333000; 330300; 303300. 20. 42. 21. 6.
259
Вариант № 8
1. 5000. 2. 3124. 3. 3. 4. 136,8. 5. 0,25. 6. 61,8. 7. 4123. 8. 23. 9. 26. 10. 4225. 11. 37,2. 12. 50. 13. 36.
14. 37,8. 15. 2125. 16. 540. 17. 2. 18. 3412. 19. 1110000; 1101000; 1011000. 20. 63. 21. 8.
Вариант № 9
1. 10550. 2. 1342. 3. 35. 4. 121,5. 5. 0,375. 6. 5. 7. 3412. 8. 13. 9. 13. 10. 280. 11. 75. 12. 35. 13. 42.
14. 25,2. 15. 6930. 16. 1260. 17. −2. 18. 3142. 19. 666000; 660600; 606600. 20. 90. 21. 5.
Вариант № 10
1. 6. 2. 4123. 3. 4. 4. 3,5. 5. 0,95. 6. 4231. 7. 24. 8. 14. 9. 19. 10. 150. 11. 41,6. 12. 105. 13. 25. 14. 3.
15. 140. 16. −9. 17. 3. 18. 2431. 19. 1600; 3125; 5400; 8575. 20. 20. 21. 8.
Вариант № 11
1. 5. 2. 3214. 3. 2. 4. 2,5. 5. 0,75. 6. 4123. 7. 13. 8. 2. 9. 32. 10. 30. 11. 16,5. 12. 85. 13. 81. 14. 5.
15. 720. 16. −5. 17. 2. 18. 4231. 19. 16875; 34992; 64827. 20. 39. 21. 17.
Вариант № 12
1. 8. 2. 2341. 3. 3. 4. 6,5. 5. 0,825. 6. 3412. 7. 1. 8. 12. 9. 10. 10. 60. 11. 16. 12. 66. 13. 64. 14. 12,5.
15. 47,5. 16. 7. 17. −1. 18. 2143. 19. 1323; 3136; 6125. 20. 37. 21. 5.
Вариант № 13
1. 148. 2. 2314. 3. 9. 4. 0,007. 5. 0,25. 6. 57. 7. 2431. 8. 1. 9. 12. 10. 8. 11. 18000. 12. 52. 13. 8. 14. 8.
15. 1530. 16. −1,5. 17. 2,5. 18. 3124. 19. 777. 20. 30. 21. 3.
Вариант № 14
1. 34. 2. 3142. 3. 0,8. 4. 0,135. 5. 0,1. 6. 48. 7. 3124. 8. 23. 9. 3. 10. 1,7. 11. 32000. 12. 68. 13. 3.
14. 12,8. 15. 5440. 16. −0,4. 17. 0,5. 18. 4312. 19. 578; 587; 758; 785; 857; 875. 20. 8. 21. 50.
Вариант № 15
1. 29. 2. 3241. 3. 18. 4. 0,0004. 5. 0,2. 6. 17. 7. 4312. 8. 14. 9. 32. 10. 1,5. 11. 12500. 12. 100. 13. 3,75.
14. 17. 15. 16800. 16. −0,75. 17. 1,6. 18. 2413. 19. 579; 597; 759; 795; 957; 975. 20. 60. 21. 0,8.
Вариант № 16
1. 230. 2. 4231. 3. 753. 4. 5. 5. 0,2. 6. 64100. 7. 4312. 8. 14. 9. 6. 10. 55. 11. 8. 12. 2. 13. 180. 14. 16,8.
15. 693,5. 16. 7. 17. 2. 18. 3124. 19. 3211. 20. 17. 21. 105.
Вариант № 17
1. 300. 2. 2134. 3. 755. 4. 7. 5. 0,3. 6. 52500. 7. 4213. 8. 13. 9. 12. 10. 20. 11. 6. 12. 6. 13. 36. 14. 2,6.
15. 513. 16. 5,5. 17. 0,6. 18. 3124. 19. 1133; 1331; 3113; 3311. 20. 10. 21. 78.
Вариант № 18
1. 20. 2. 2134. 3. 2. 4. 1,5. 5. 0,997. 6. 3024. 7. 1243. 8. 24. 9. 28. 10. 0,862. 11. 9. 12. 48. 13. 40.
14. 800. 15. 5000. 16. 420. 17. −3. 18. 4132. 19. 122112; 212112; 221112. 20. 48. 21. 70.
Вариант № 19
1. 9. 2. 4231. 3. 1. 4. 8. 5. 0,998. 6. 2040. 7. 4312. 8. 13. 9. 21. 10. 0,1502. 11. 16. 12. 12. 13. 80. 14. 3,8.
15. 12000. 16. 850. 17. 1. 18. 4132. 19. 122112; 212112; 221112. 20. 44,8. 21. 35.
Вариант № 20
1. 880. 2. 3214. 3. 4. 4. 200. 5. 0,4. 6. 42500. 7. 1432. 8. 24. 9. 15. 10. 120. 11. 18. 12. 25. 13. 3. 14. 10.
15. 300. 16. 150. 17. 3. 18. 4231. 19. 63036; 63630; 69696. 20. 24. 21. 60.
260
Вариант № 21
1. 685. 2. 2134. 3. 15. 4. 180. 5. 0,6. 6. 52500. 7. 1432. 8. 12. 9. 20. 10. 150. 11. 48. 12. 12,5. 13. 2.
14. 7. 15. 220. 16. 15. 17. 11. 18. 3412. 19. 46464; 46420; 42020. 20. 2,4. 21. 20.
Вариант № 22
1. 8. 2. 1432. 3. 65. 4. 4. 5. 0,3. 6. 250. 7. 4321. 8. 14. 9. 12. 10. 18. 11. 31. 12. 36. 13. 24. 14. −1,5.
15. 976,5. 16. −0,8. 17. −0,6. 18. 2413. 19. 917; 973. 20. 14. 21. 10.
Вариант № 23
1. 9. 2. 4231. 3. 15. 4. 2,5. 5. 0,1. 6. 320. 7. 3124. 8. 14. 9. 8. 10. 26,25. 11. 28. 12. 12. 13. 28. 14. 1.
15. 725. 16. 0,6. 17. 2,4. 18. 4312. 19. 532. 20. 16. 21. 35.
Вариант № 24
1. 10. 2. 4321. 3. 6. 4. 30. 5. 0,84. 6. 77070. 7. 2143. 8. 12. 9. 25. 10. 1000. 11. 96. 12. 2. 13. 2520.
14. −3. 15. 22. 16. 3. 17. −3. 18. 3214. 19. 147; 357; 567; 777; 987. 20. 2. 21. 21.
Вариант № 25
1. 12. 2. 2143. 3. 3. 4. 60. 5. 0,96. 6. 51380. 7. 2143. 8. 34. 9. 28. 10. 1340. 11. 150. 12. 2. 13. 2160.
14. 6. 15. 19. 16. 2. 17. 11. 18. 4123. 19. 159; 234; 468; 543; 852. 20. 3. 21. 18.
Вариант № 26
1. 22. 2. 2143. 3. 16. 4. 22. 5. 0,243. 6. 27900. 7. 4213. 8. 24. 9. 3. 10. 420. 11. 2000. 12. 1,6. 13. 35.
14. 12. 15. 2200. 16. −0,5. 17. 5,5. 18. 1423. 19. 331; 586; 841. 20. 18. 21. 31.
Вариант № 27
1. 11. 2. 3124. 3. 10. 4. 11,2. 5. 0,4116. 6. 29050. 7. 2143. 8. 4. 9. 2. 10. 170. 11. 168. 12. 9,1. 13. 12.
14. 18. 15. 5600. 16. 0,5. 17. 5. 18. 1243. 19. 199; 430; 661; 892. 20. 15. 21. 16.
Вариант № 28
1. 34. 2. 4321. 3. 18. 4. 6. 5. 0,288. 6. 30000. 7. 2413. 8. 2. 9. 4. 10. 32. 11. 288. 12. 4,2. 13. 16. 14. 256.
15. 4300. 16. 0,8. 17. 627. 18. 2341. 19. 105; 490; 875. 20. 18. 21. 39.
Вариант № 29
1. 8. 2. 4321. 3. 7. 4. 2. 5. 0,1. 6. 180000. 7. 2341. 8. 13. 9. 8. 10. 86. 11. 14400. 12. 90. 13. 63. 14. 0,5.
15. 25500. 16. −1. 17. 1. 18. 2143. 19. 142857. 20. 1,5. 21. 19.
Вариант № 30
1. 12. 2. 4231. 3. 20. 4. 1372. 5. 0,25. 6. 172800. 7. 2341. 8. 13. 9. 12. 10. 114. 11. 35000. 12. 135.
13. 70. 14. 0,5. 15. 48000. 16. −1. 17. 1. 18. 2413. 19. 102564. 20. 160. 21. 5.
261
СПРАВОЧНЫЕ МАТЕРИАЛЫ
АЛГЕБРА
Таблица квадратов целых чисел от 0 до 99
Десятки
Единицы
0
1
2
3
4
5
6
7
8
9
0
0
1
4
9
16
25
36
49
64
81
1
100
121
144
169
196
225
256
289
324
361
2
400
441
484
529
576
625
676
729
784
841
3
900
961
1024
1089
1156
1225
1296
1369
1444
1521
4
1600
1681
1764
1849
1936
2025
2116
2209
2304
2401
5
2500
2601
2704
2809
2916
3025
3136
3249
3364
3481
6
3600
3721
3844
3969
4096
4225
4356
4489
4624
4761
7
4900
5041
5184
5329
5476
5625
5776
5929
6084
6241
8
6400
6561
6724
6889
7056
7225
7396
7569
7744
7921
9
8100
8281
8464
8649
8836
9025
9216
9409
9604
9801
Свойства арифметического квадратного корня:
ab
=
a
a
при a ≥ 0, b > 0 .
=
b
b
a ⋅ b при a ≥ 0, b ≥ 0;
Корни квадратного уравнения ax 2 + bx + c= 0, a ≠ 0 :
x1 =
−b − b 2 − 4ac
−b + b 2 − 4ac
, x2 =
при b 2 − 4ac > 0 ;
2a
2a
x=
−b
0.
при b 2 − 4ac =
2a
Формулы сокращённого умножения:
(a + b) 2 =a 2 + 2ab + b 2 ;
(a − b)2 =a 2 − 2ab + b 2 ;
a 2 − b 2 = (a + b)(a − b) .
Степень и логарифм:
Свойства степени
при a > 0, b > 0
a−n =
n
1
a
n
a ⋅a =
a n+ m
an
am
an
m
=a
( )
m
n−m
= a nm
n
(ab)=
a n ⋅ bn
262
Свойства логарифма
при a > 0, a ≠ 1, b > 0, x > 0, y > 0
a log a b = b
log a a = 1
log a 1 = 0
log=
a xy log a x + log a y
x
log
log a x − log a y
=
a
y
log a b k = k log a b
ГЕОМЕТРИЯ
Средняя линия треугольника и трапеции
MN – ср. лин.
B
B
C
BC AD
MN AC
M
N
A
MN – ср. лин.
AC
MN =
2
C
M
N
A
D
MN AD
MN =
Теорема
Пифагора:
2
2
Длина окружности
C = 2πr
r
2
a +b =
c .
c
BC + AD
2
Площадь круга S = πr 2
a
α
b
Правильный треугольник
R=
a
R
S=
a 3
3
a
2
a 3
6
h=
a 3
2
a
h
r
3
r=
4
Площади фигур
Параллелограмм
b
S = aha
Треугольник
1
S = aha
2
=
S ab sin γ
ha
b
γ
a
ha
=
S
γ
1
ab sin γ
2
a
Трапеция
b
Ромб
a+b
=
S
⋅h
2
d1 , d 2 – диагонали
1
S = d1d 2
2
d1
ha
d2
a
Площади поверхностей и объемы тел
Прямоугольный параллелепипед
Прямая призма
h
c
b
Sосн
a
263
Пирамида
Конус
h
h
l
r
Sосн
Цилиндр
Шар
r
h
r
Тригонометрические функции
Прямоугольный треугольник
Тригонометрическая окружность
sin α =
c
a
c
b
cos α =
c
a
α
tg α =
b
1
Pα
cosα
sinα
α
1
a
b
Основное тригонометрическое тождество: sin 2 α + cos 2 α =1 .
Некоторые значения тригонометрических функций
α
0°
градусы
sin α
0
cos α
1
tg α
0
30°
45°
60°
1
2
3
2
3
3
2
2
2
2
3
2
1
2
1
3
90°
180°
270°
360°
1
0
−1
0
0
−1
0
1
–
0
–
0
Функции
Линейная функция
Производная функции в точке x0
y
y
α
y = kx + b
b
0
α
k = tgα
264
α
x
0
y = f(x)
x0
fʹ(x0) = tgα
x
СПИСОК ЛИТЕРАТУРЫ
1.
2.
3.
4.
5.
6.
7.
Демонстрационный вариант контрольных измерительных материалов единого государственного
экзамена 2024 года по МАТЕМАТИКЕ. (Сайт «ФИПИ»)
Спецификация контрольных измерительных материалов для проведения в 2024 году единого государственного экзамена по МАТЕМАТИКЕ Базовый уровень. (Сайт «ФИПИ»)
Федеральная образовательная программа среднего общего образования. (Приказ Министерства
просвещения Российской Федерации от 23.11.2022 № 1014 от 23.11.2022 г.)
Федеральный закон от 24.09.2022 № 371-ФЗ «О внесении изменений в Федеральный закон «Об
образовании в Российской Федерации» и статью 1 Федерального закона «Об обязательных требованиях в Российской Федерации».
Математика: алгебра и начала математического анализа., геометрия. Алгебра и начала математического анализа. 10–11 классы: учеб. для общеобразоват. организаций : базовый и углубл. уровни
/ [Ш.А. Алимов, Ю.И. Калягин, М.В. Ткачева и др.]. – 11-е изд. – М.: Просвещение. – 2023.
Геометрия. 10-11 классы: учеб. для общеобразоват. организаций : базовый и углубл. уровни / [Л.С.
Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 3-е изд. – М.: Просвещение. – 2016.
Сборник задач по математике для подготовительных курсов. Часть I. Алгебра и начала анализа. /
[С.Г. Кальней, Т.А. Олейник, А.А. Прокофьев]. – 7-е изд. – М.: МИЭТ. – 2008.
8. Пособие по математике для подготовительных курсов. Часть II. (Планиметрия) / А.А. Прокофьев.
– 4-е изд. перераб. и доп. – М.: МИЭТ. – 2007.
9. Пособие по математике для подготовительных курсов. Часть III. (Стереометрия) / А.А. Прокофьев.
– М.: МИЭТ. – 2001.
Интернет-ресурсы
1. https://fipi.ru
2. https://alexlarin.net
265
СОДЕРЖАНИЕ
Предисловие ...............................................................................................................................................
3
Глава 1. АЛГЕБРА, НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА,
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СТАТИСТИКА .......................................................................
4
§ 1. Числа и вычисления ..........................................................................................................................
4
1.1. Дроби .........................................................................................................................................
4
Проверочная работа № 1 ................................................................................................................
5
1.2. Степень с целым показателем ................................................................................................
6
Проверочная работа № 2 ................................................................................................................
7
1.3. Иррациональные числа ...........................................................................................................
7
Проверочная работа № 3 ................................................................................................................
8
1.4. Логарифмы ................................................................................................................................
8
Проверочная работа № 4 ................................................................................................................
9
1.5. Тригонометрические выражения ............................................................................................ 10
Проверочная работа № 5 ................................................................................................................ 10
1.6. Координатная прямая .............................................................................................................. 11
1.7. Числа и их свойства ................................................................................................................ 17
Проверочная работа № 6 ................................................................................................................ 18
§ 2. Уравнения............................................................................................................................................ 19
Проверочная работа № 7 ................................................................................................................ 22
§ 3. Неравенства ........................................................................................................................................ 23
Проверочная работа № 8 ................................................................................................................ 26
§ 4. Текстовые задачи ............................................................................................................................... 27
4.1. Размеры и единицы измерения. ............................................................................................. 27
4.2. Формулы .................................................................................................................................... 31
Проверочная работа № 9 ................................................................................................................ 34
4.3. Простейшие текстовые задачи (округление) ........................................................................ 35
Проверочная работа № 10 .............................................................................................................. 38
4.4. Простейшие текстовые задачи (части) .................................................................................. 39
Проверочная работа № 11 .............................................................................................................. 42
4.5. Выбор оптимального варианта............................................................................................... 42
Проверочная работа № 12 .............................................................................................................. 47
4.6. Текстовые задачи (движение, работа, растворы) ................................................................. 47
Проверочная работа № 13 .............................................................................................................. 53
4.7. Анализ утверждений ............................................................................................................... 53
Проверочная работа № 14 .............................................................................................................. 57
4.8. Задачи на смекалку .................................................................................................................. 57
§ 5. Анализ диаграмм и графиков........................................................................................................... 60
Проверочная работа № 15 .............................................................................................................. 75
266
§ 6. Теория вероятностей ......................................................................................................................... 77
Проверочная работа № 16 .............................................................................................................. 81
Глава 2. ГЕОМЕТРИЯ .............................................................................................................................. 83
§ 7. Планиметрия ....................................................................................................................................... 83
7.1. Прикладные задачи по планиметрии .................................................................................. 83
Проверочная работа № 17 ........................................................................................................... 86
Проверочная работа № 18 ........................................................................................................... 90
7.2. Углы и длины ......................................................................................................................... 91
Проверочная работа № 19 .............................................................................................................. 97
7.3. Площади .................................................................................................................................... 98
Проверочная работа № 20 .............................................................................................................. 100
7.4. Окружность ............................................................................................................................... 101
Проверочная работа № 21 .............................................................................................................. 103
§ 8. Стереометрия ...................................................................................................................................... 104
8.1. Прикладные задачи по стереометрии.................................................................................... 104
Проверочная работа № 22 .............................................................................................................. 108
8.2. Задачи по стереометрии .......................................................................................................... 109
Проверочная работа № 23 .............................................................................................................. 116
Глава 3. ТРЕНИРОВОЧНЫЕ ВАРИАНТЫ ............................................................................................ 117
Вариант № 1 .................................................................................................................................... 117
Вариант № 2 .................................................................................................................................... 121
Вариант № 3 .................................................................................................................................... 125
Вариант № 4 .................................................................................................................................... 129
Вариант № 5 .................................................................................................................................... 133
Вариант № 6 .................................................................................................................................... 137
Вариант № 7 .................................................................................................................................... 141
Вариант № 8 .................................................................................................................................... 145
Вариант № 9 .................................................................................................................................... 149
Вариант № 10 .................................................................................................................................. 153
Вариант № 11................................................................................................................................... 157
Вариант № 12 .................................................................................................................................. 161
Вариант № 13 .................................................................................................................................. 165
Вариант № 14 .................................................................................................................................. 170
Вариант № 15 .................................................................................................................................. 175
Вариант № 16 .................................................................................................................................. 180
Вариант № 17 .................................................................................................................................. 185
Вариант № 18 .................................................................................................................................. 190
Вариант № 19 .................................................................................................................................. 194
Вариант № 20 .................................................................................................................................. 198
267
Вариант № 21 .................................................................................................................................. 203
Вариант № 22 .................................................................................................................................. 208
Вариант № 23 .................................................................................................................................. 213
Вариант № 24 .................................................................................................................................. 218
Вариант № 25 .................................................................................................................................. 223
Вариант № 26 .................................................................................................................................. 228
Вариант № 27 .................................................................................................................................. 233
Вариант № 28 .................................................................................................................................. 238
Вариант № 29 .................................................................................................................................. 243
Вариант № 30 .................................................................................................................................. 248
Ответы............................................................................................................................................... 253
Справочные материалы................................................................................................................... 262
Список литературы ......................................................................................................................... 265
268