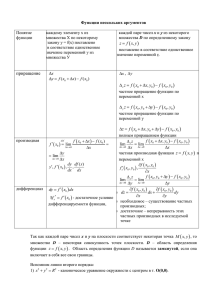
Дадим аргументу х приращение Δх, а аргументу у приращение Δу. Тогда функция z получит значение f (x x, y y) Величина z f (x x, y y) f ( x, y ) называется полным приращением функции в точке (х,у). Если задать только приращение х или у, то x z f (x y z f ( x, y x, y) f ( x, y) y) f ( x, y ) - частные приращения функции. Полное приращение функции в общем случае не равно суме частных приращений: z x z y z Найти полное и частные приращения функции z x y x z x y y z (x x) y x y x y x y x (y x y x x y y) x y y x y x y z ( x x) ( y y ) x y x y x y x y x y x y x y x y x y Действительно z x z y z Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной, при стремлении приращения переменной к нулю. zx , z y , z , x z , y f x ( xy), f y ( xy) zx zy z x lim x lim y x y 0 0 z y lim x 0 lim y f (x 0 f ( x, y x, y ) x f ( x, y ) y) y f ( x, y ) Из определения частной производной следует, что для нахождения производной zx нужно считать постоянной переменную у, а для нахождения производной z y нужно считать постоянной переменную х. При нахождении частных производных сохраняются известные ранее правила дифференцирования. Найти частные производные функции z x ln y y x z x zx zy z y ln y y 2 x x y 1 x Введем понятие частных производных второго порядка. Если частные производные zx z x и zy z y сами являются дифференцируемыми функциями, то можно найти их частные производные, которые называются частными производными второго порядка: z xx z yy f xx ( xy) f yy ( xy) 2 z x 2 2 z y 2 Можно также производные: определить смешанные 2 z xy f xy ( xy) z x y 2 z yx f yx ( xy) z y x Если частные производные второго порядка функции z=f(x,y) непрерывны в точке (х0,у0), то в этой точке смешанные производные равны: f xy ( x0 , y0 ) f yx ( x0 , y0 ) Вычислить частные производные второго порядка функции z 3x 2 x sin y в точке (1,0). z x zx 6 x sin y 2 z xx z x2 6 zy z yy 2 z xy z x y z y 2 z y 2 x cos y x sin y 2 cos y z yx z y x cos y z xx (1,0) 6 z xy (1,0) 0 z yy (1,0) z yx (1,0) 0 0