Лабораторная работа №9. ИСПОЛЬЗОВАНИЕ НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ СОГЛАСИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ ОБ ОДНОРОДНОСТИ

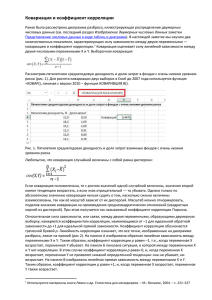
Лабораторная работа №9.
ИСПОЛЬЗОВАНИЕ НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ
СОГЛАСИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ ОБ ОДНОРОДНОСТИ
ВЫБОРОЧНЫХ ДАННЫХ.
Проверка однородности распределений.
Для проверки однородности обычно используются диаграммы
рассеяния. Это наиболее удобный способ визуального
исследования зависимости двух переменных, поскольку они
предоставляют больше информации, чем простое значение
коэффициента корреляции. Например, отсутствие однородности в
выборке, для которой была подсчитана корреляция, может исказить
значение коэффициента корреляции.
Предположим, вычисления производились для данных из
различных экспериментальных групп, но этот факт не был учтен, то
есть группировка не проводилась. Можно предположить, что
экспериментальные действия в одной из групп увеличили значения
обеих коррелированных переменных, и таким образом, данные из
каждой группы образуют отдельное «облако» на диаграмме
рассеяния.
Исследование диаграмм рассеяния позволяет определять
формы зависимостей, чтобы потом можно было выбрать
подходящий тип преобразования данных для их «линеаризации»
или выбора подходящего нелинейного уравнения подгонки. Кроме
того, важным преимуществом диаграмм рассеивания, является то,
что они позволяют находить «выбросы» (нетипичные данные),
которые искусственным образом увеличивают или уменьшают
(«смещают») коэффициент корреляции. Даже один выброс может
значительно увеличить коэффициент корреляции между двумя
переменными. Диаграмма рассеяния позволяет обнаруживать такие
аномалии.
В данной лабораторной работе мы будем использовать
простые диаграммы рассеивания, которые визуализируют
зависимость между двумя переменными. Данные изображаются
точками в двумерном пространстве, где оси соответствуют
переменным.
Для того, что бы получить диаграмму рассеяния, необходимо
выполнить следующие действия:
1. В системе Statistica открываем ранее созданный файл.
2. Выбираем пункт меню «Графика» – «Статистические 2Ь
графики»-«Диаграммы рассеяния».
3. Задайте в качестве переменных X и Y, названия
переменных вашей таблицы.
4. Нажмите ОК. По умолчанию будет построена диаграмма
рассеяния с графиком линейной регрессии.
5. Попытайтесь построить диаграмму без графика линейной
регрессии самостоятельно.
Построение корреляционных взаимосвязей (корреляционной
матрицы).
Ключевым
понятием,
описывающим
связи
между
переменными, является корреляция. В данной лабораторной работе
мы будем иметь дело с, так называемой, парной корреляцией.
Значение коэффициента парной корреляции изменяется в пределах
от –1 до +1. Крайние значения имеют особенный смысл. Значение –
1 означает полную отрицательную зависимость, значение +1
означает полную положительную зависимость, иными словами,
между наблюдаемыми переменными имеется точная линейная
зависимость
с
отрицательным
или
положительным
коэффициентом. Значение 0,00 интерпретируется как отсутствие
корреляции. Таким образом, корреляция определяет степень, с
которой значения двух переменных пропорциональны друг другу.
Две переменные положительно коррелированны, если при
увеличении одной переменной увеличиваются значения другой
переменной.
Две переменные отрицательно коррелированны, если при
увеличении одной переменной другая переменная уменьшается.
Коэффициент корреляции – безмерная величина и не зависит
от масштаба измерения.
Для того, что бы получить значение коэффициента
корреляции в программе Statistica необходимо выполнить
следующие действия:
1. в системе Statistica откройте ранее созданный файл с данными.
2. в стартовой панели выберите пункт меню «Статистика»\
«Основные статистики и таблицы».
3. в появившемся окне выберите процедуру «Корреляционные
матрицы» (Correlation matrices) и щелкните «ОК» (или просто
дважды щелкните на процедуре «Корреляционные матрицы»).
4. в появившемся диалоговом окне нажмите кнопку Summary:
Correlation matrix
и, в появившемся окне, выберите
переменные,
между
которыми
будете
оценивать
корреляционные связи.
5. Оцените полученную зависимость между переменными.