ЛабМножеств_лин_регрессия

Множественный линейный
корреляционно-регрессионный
анализ
ПРОДОЛЖЕНИЕ
Корреляционный анализ, разработанный К. Пирсоном и
Дж. Юлом, является одним методов статистического
анализа взаимозависимости нескольких признаков
(случайных величин).
Одним из основных показателей взаимозависимости двух
случайных величин является парный коэффициент
корреляции, служащий мерой линейной статистической
зависимости между этими величинами. Следовательно,
этот показатель соответствует своему прямому
назначению, когда статистическая связь между
соответствующими признаками в генеральной
совокупности линейна. То же самое касается частных и
совокупных коэффициентов корреляции. Одним из
требований, определяющий корреляционный метод,
является требование линейности статистической связи и
нормальность.
Множественная линейная регрессия
В случае, когда коэффициент детерминации мал
(степень этого определяется самим исследователем)
возникает вопрос об улучшении качества модели за счет
введения новых регулируемых переменных, приходя к
линейной модели вида
y=b0+b1x1+b2x2+…+akxk,
где x1,x2, …, xk – входные переменные, либо за счет
усложнения модели, делая ее квадратичной,
логарифмической, показательной, то есть, выбирая ее в
виде:
y  a 0  a 1x ,
2
либо
y  a 0  loga 1 x,
либо
a1
y  a0  x ,
Рассмотрим случай двух независимых
переменных.
Предположим что, зависимость между переменными
имеет вид
y=b0+b1x1+b2x2
(1)
где переменные x1 и x2 принимают заданные
фиксированные значения, причём между
переменными x1 и x2 нет линейной зависимости.
Результаты наблюдений (x1i, x2i, yi), i=1, 2, …, n,
представляются в виде
yi=b0+b1x1i+b2x2i+εi .
Оценки параметров модели (1) могут быть найдены
по формуле
b  A A AT Y
T
1
 y1 
 
где Y=  y 2  - вектор наблюдений
 
 
 yn 
 b0 
 
b=  b1 
 
 
b 
 n
— вектор МНК — оценок
параметров модели (1);
1 x 11 x 21 


1 x 12 x 22 

A=
 


1 x 1n x 2n 
Регрессивная матрица
Предположим, что ошибки наблюдений εi
независимы, имеют равные дисперсии и
нормально распределены. В этом случае можно
проверить гипотезу H0: b1=b2=0. Эта гипотеза
позволяет установить, находятся ли переменные x1
и x2 во взаимосвязи с y. Статистикой критерия для
проверки гипотезы H0 является отношение
SS D / 2
F
SS R /( n  3)
Если выборочное значение этой статистики
Fв> F1 (2, n  3) ,
то гипотеза H0 отклоняется; в противном случае
следует считать, что взаимосвязи y с переменными
x1 и x2 нет.
Мультиколлинеарность входных переменных
Рассмотрим такое неприятное явление для
регрессионного анализа, как мультиколлинеарность
независимых переменных. Мультиколлинеарностью
называется наличие линейной связи между
независимыми переменными, в нашем случае между
X1 и X2.
Мультиколлинеарность может проявляться в двух
видах: в функциональной зависимости между X1 и X2,
например X2=b0+b1X1, либо, наоборот. Определитель
информационной матрицы равен нулю, т.е. матрица
вырожденная. Такой вид мультиколлинеарности, как
правило, встречается крайне редко. Гораздо чаще
мультиколлинеарность наблюдается в стохастической
форме.
Оценку силы мультиколлинеарности можно
произвести, вычислив коэффициенты корреляции
между коэффициентами bi и bj .Для того, чтобы
оценки коэффициентов были независимыми,
необходимо, чтобы в матрице Фишера (XTX) только
диагональные элементы были отличны от нуля.
Пример. Данные, полученные из годовых
отчетов десяти предприятий: Y – себестоимость
товарной продукции (млн. руб.), X1 – объём
валовой продукции (млн. руб.) и X2 
производительность труда (тыс. руб. на чел.).
Таблица 1. Данные по 10 предприятиям
Y
2,1
2,8
3,2
4,5
4,8
4,9
5,5
6,5
12,1
15,0
X1
3
4
5
5
5
5
6
7
15
20
X2
1.8
1,5
1,4
1,3
1,3
1,5
1,6
1,2
1,3
1,2
Проведём корреляционный анализ
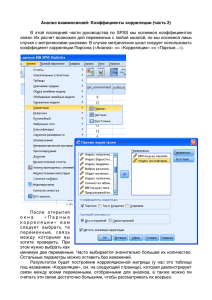
Раскрываем окно электронной таблицы и вводим
числовые данные. Для обозначения переменных
последовательно маркируем колонки и щелчком
правой кнопки мышки вызываем меню, из которого
выбираем пункт Modify column, где вводим нужные
имена столбцов (колонок). Сохраняем файл под
именем, например, factory (в нашей демоверсии нет
такой возможности). Получаем таблицу 1,
представленную на рис.1.
Появляется рабочее поле анализа множества
переменных со сводкой, в которой подтверждается,
что три переменные (по 10 наблюдений в каждой)
приняты к обработке. Нажимаем кнопку табличных
опций (вторая слева в нижнем ряду) и выбираем
Correlations. На экране выдаётся таблица
корреляций. В данной таблице первое число
является коэффициентом корреляции Пирсона,
второе (под первым) представляет количество
наблюдений, третий уровень значимости
Таблица 2. Таблица корреляций (Correlations)
X1
X1
X2
Y
-0.5650
(10)
0.0888
0.9872
(10)
0.0000
X2
-0.565
(10)
0.0888
-0.6050
(10)
0.0639
Y
0.9872
(10)
0.0000
-0.6050
(10)
0.0639
Correlation
Из полученных данных следует, что очень сильная
положительная связь наблюдается между переменными
Y (себестоимость товарной продукции) и X1 (объём
валовой продукции). Степень доверия к этой связи,
исходя из уровня значимости, почти 100%.
Другие связи менее выражены, но, однако заслуживают
внимания, т.к. доверие к ним более 90% (р<0.1). Это
отрицательная связь Y c X2 (производительность труда) и
отрицательная связь X1 и X2.
Можно построить диаграммы рассеивания на плоскости,
образуемых различными парами переменных. Для этого
нажимаем кнопку графических опций (третья слева в
нижнем ряду) и устанавливаем флажок Scatterplot Matrix
(матрица рассеивания) (см. рис 1.). Получаем
графическое отображение (см. рис. 2).
Рис. 1. Устанавливаем флажок Scatterplot
Matrix
Рис. 2. Диаграммы рассеивания на плоскости
Multiple Regression Analysis
Множественный регрессионный анализ
Зависимая переменная: Y
Parameter
Estimat
Standard T Statistic
(T –
(Параметры) (Оценки) Error
статистика)
CONSTANT
0,367639 0,388886 0,945365
X1
0,818195 0,065241 12,5411
X2
-0,146225 0,107285 -1,36296
P-Value
(P –значение)
0,3760
0,0000
0,2151
Analysis of Variance
(Дисперсионный анализ)
Source
(источник)
Model
Residual
Sum of Df Mean
Squares
Square
153,555 2 76,7775
3,14905 7 0,449864
F-Ratio
P-Value
170,67
0,0000
Total (Corr.)
156,704
9
R-squared = 97,9904 percent
R-squared (adjusted for d.f.) = 97,4163 percent
Standard Error of Est. = 0,670719
Mean absolute error = 0,496893
Durbin-Watson statistic = 0,963907
R-squared = 97,9904 процента
R-squared (откорректированный для d.f.) =
97,4163 процента
Стандартная Ошибка Оценки. = 0,670719
Средняя{Скупая} абсолютная погрешность =
0,496893
Durbin-Уотсон, статистический = 0,963907
The StatAdvisor
The output shows the results of fitting a multiple linear
regression model to describe the relationship between Y
and 2 independent variables. The equation of the fitted
model is
Y = 0,367639 + 0,818195*X1 - 0,146225*X2
Since the P-value in the ANOVA table is less than 0.01,
there is a statistically significant relationship between the
variables at the 99% confidence level.
The R-Squared statistic indicates that the model as fitted
explains 97,9904% of the variability in Y. The adjusted Rsquared statistic, which is more suitable for comparing
models with different numbers of independent variables, is
97,4163%. The standard error of the estimate shows the
standard deviation of the residuals to be 0,670719.
This value can be used to construct prediction limits for
new observations by selecting the Reports option from
the text menu. The mean absolute error (MAE) of
0,496893 is the average value of the residuals. The
Durbin-Watson (DW) statistic tests the residuals to
determine if there is any significant correlation based
on the order in which they occur in your data file. Since
the DW value is less than 1.4, there may be some
indication of serial correlation. Plot the residuals versus
row order to see if there is any pattern which can be
seen.
In determining whether the model can be
simplified, notice that the highest P-value on the
independent variables is 0,2151, belonging to X2.
Since the P-value is greater or equal to 0.10, that
term is not statistically significant at the 90% or
higher confidence level. Consequently, you should
consider removing X2 from the model. 95,0%
confidence intervals for coefficient estimates.
СтатКонсультант
Консультант показывает результаты построения
множественной линейной регрессии, чтобы описать
отношения между Y и 2 - мя независимыми
переменными. Уравнение регрессионной модели имеет
вид
Y = 0,367639 + 0,818195*X1 - 0,146225*X2.
Так как P-значение в ANOVA таблице меньше чем 0.01,
есть a статистически существенные отношения между
переменными в 99% - ый уровень надёжности.
R-Squared статистический указывает долю дисперсии
зависимой переменной, обусловленную изменением
независимых переменных, т.е. 97,9904 % изменчивости в
Y.
Отрегулированный R-squared статистический,
который является более подходящим для того,
чтобы сравнить модели с различным числом
независимых переменных, являются 97,4163 %.
Стандартная ошибка оценка показывает
стандартное отклонение ошибок, чтобы быть
0,670719. Эта ценность может использоваться,
чтобы строить пределы предсказания для новых
наблюдений, выбирая опцию Сообщений отменю
текста.
Средняя абсолютная ошибка (БОЛЬШЕ) 0,496893 средняя ценность остатков. Durbin-Уотсон
(СОБСТВЕННЫЙ ВЕС) статистические испытания остатков
к определите, есть ли любая существенная корреляция,
основанная на заказе {порядке} в котором они
происходят в вашем файле данных. Так как ценность
СОБСТВЕННОГО ВЕСА – меньше чем 1.4, может быть
некоторый признак последовательной корреляции.
График остатков против ряда заказывают, чтобы видеть,
есть ли любой образец который может быть замечен.
Заметим, что построенная модель может быть упрощена,
так как самое большое P-значение для независимых
переменных – 0,2151, принадлежит X2. Если P-значение
больше или равна 0.10, то элемент – статистически
несущественный в 90%-ом или более высокий уровень
надёжности.
Следовательно, Вы должны рассмотреть удаление X2 из
модели. доверительные интервалы на 95,0 % для
оценок коэффициента.
Lower
Parameter Standard Error
Upper Limit
Estimate
Limit
CONSTANT 0,367639 0,388886 -0,551933 1,28721
X1
0,818195 0,065241 0,663924 0,972466
X2
0,146225 0,107285 -0,399915 0,107465
Мультиколлинеарность
Матрица корреляции для оценок коэффициентов
модели
CONSTANT
X1
X2
CONSTANT
1,0000
-0,7208
0,2975
X1
-0,7208
1,0000
-0,7824
X2
0,2975
-0,7824
1,0000
СтатКонсультант
Эта таблица показывает оцененные корреляции между
коэффициентами в построенной модели. Эти
корреляции могут использоваться, чтобы обнаружить
присутствие серьезной мультиколлинеарности, то есть,
корреляция среди переменных. В этом случае, есть
одна корреляция с абсолютное значение больше чем
0.5 (исключая постоянный элемент CONSTANT).
ПРОДОЛЖЕНИЕ СЛЕДУЕТ