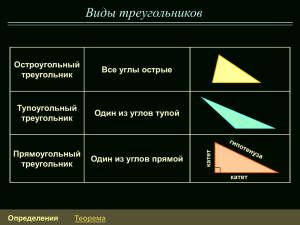
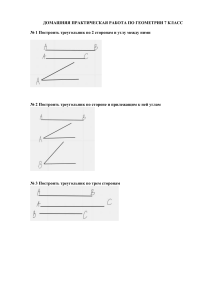
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ <<ОРСКИЙ ТЕХНИЧЕСКИЙ ТЕХНИКУМ ИМЕНИ А.И. СТЕЦЕНКО>> ФИЛИАЛ П.ЭНЕРГЕТИК Индивидуальный проект Тема: «Треугольники » Выполнил: Специальность: Группа: 5 Проверил: руководитель Николаева Наталья Юрьевна Актуальность На на уроках геометрии мы подробно познакомились с геометрической фигурой – треугольником. Оказалось, что мы многого не знали. Треугольник по праву считается простейшей из фигур: любая плоская, то есть простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки, не лежащие на одной прямой. Треугольник всегда имел широкое применение в практической жизни. Для того, чтобы узнать ещё больше об этой фигуре, поставила цель: я решила провести небольшое исследование, систематизировать и расширить знания о треугольнике в нашей жизни. Задачи проекта: 1.Используя толковые словари русского языка, найти значение термина треугольник. 2.Рассмотреть основные виды треугольников и дать определение, каждого из этих треугольников. 3.Изучить историю возникновения треугольника. 4.Узнать о применении треугольников в практической жизни. ОПРЕДЕЛЕНИЕ ТЕРМИНА «ТРЕУГОЛЬНИК» Определение слова «треугольник» в толковых словарях русского языка Толковый словарь Ожегова С.И. Геометрическая фигура — многоугольник с тремя углами, а также всякий предмет, устройство такой формы. В зависимости от величин углов различают следующие виды треугольников. Название Определение Остроугольный Треугольник, у которого все углы являются острыми. Прямоугольный Треугольник, у которого один из углов прямой. Тупоугольный Треугольник, у которого один из углов тупой. Рисунок В зависимости от соотношения длин сторон различают следующие виды треугольников. Название Определение Разносторонний Треугольник, у которого все стороны имеют различную длину. Равнобедренный Треугольник, у которого две его стороны равны между собой. Сторона, не равная двум другим, называется его основанием. Равносторонний Треугольник, у которого все три его стороны равны между собой. Рисунок История появления треугольника Изображение треугольников и задачи на треугольники встречаются в египетских папирусах, которым более 4000 лет, в старинных индийских книгах и других древних документах. Уже тогда была известна теорема, получившая впоследствии название теоремы Пифагора, которая применялась для построения прямых углов на местности с помощью веревочного треугольника со сторонами 3, 4, 5 (египетский треугольник). Древнее землемеры выполняли геометрические построения, измеряли длины и площади; астрологии рассчитывали расположение небесных светил – всё это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике. По Кандинскому, именно линия и цветовое пятно, а не сюжет являются носителями духовного начала, их сочетания рождают «внутренний звук», вызывающий отклик в душе зрителя. Наряду с треугольниками и квадратами композиции включали в себя круг как символ совершенства и полноты мироздания. ТРЕУГОЛЬНИК, самозвучащий музыкальный инструмент — стальной прут, согнутый в виде треугольника, по которому ударяют палочкой. Применяется в оркестрах и инструментальных ансамблях. . В В западной части Атлантического океана, у юго-восточных берегов Соединённых Штатов Америки, есть район, приблизительно напоминающий по форме треугольник. Стороны его тянутся от точки севернее Бермудских островов к югу Флориды, затем вдоль Багамских островов к острову ПуэртоРико, где снова поворачивают на север и возвращаются к Бермудам около 40 градуса западной долготы. Это – одно из самых удивительных и загадочных мест на Земле. В этом районе, обычно именуемом Бермудским треугольником, исчезли без следа (после 1945 года) более 100 самолётов и судов (в том числе подводных лодок) и более тысячи человек. 4. Солдатский треугольник. Солдатское письмо без конверта, свёрнутое уголком, которое отправлялось солдатами во время войны. ТРЕУГОЛЬНИК (лат. Triangulum), созвездие Северного полушария; с территории России лучше всего видно в конце лета, осенью и зимой. Треугольник Пенроуза невозможный объект. Плоский рисунок может обманывать, изображая невозможное. Закройте одну из вершин этого треугольника, и станет ясно, что одна из его сторон направлена к нам, а другая от нас, т.е. они не могут соединиться в пространстве. Пятнадцать бильярдных шаров, которые в начале игры выкладывают треугольником на столе не раскатываются. Заключение Треугольник - простейшая плоская фигура: три вершины и три стороны. Но с древнейших времен и до наших дней математики занимаются изучением треугольника. За это время было сделано много важных открытий и даже создана новая наука – тригонометрия. Исходя из всего этого, можно сделать вывод, что треугольник является важнейшей и неисчерпаемой фигурой в геометрии и в нашей жизни.