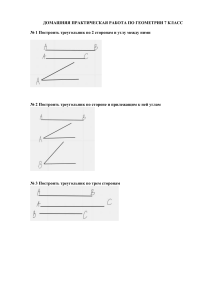
неравенством треугольника

Неравенство треугольника
Наверное, каждому из вас в детстве приходилось составлять треугольник из трех
палочек. И были случаи, что треугольник просто никак не желал складываться.
Одна палочка оказывалась длиннее других и ничего не получалось. В чем же
дело? Оказывается, не из любых трех отрезков можно сложить треугольник.
В каждом треугольнике любая сторона меньше суммы двух других сторон.
Это простое утверждение принято называть неравенством треугольника.
Оно как раз и дает ответ на вопрос: когда можно построить треугольник,
сторонами которого являются заданные отрезки a, b и c ? Такой треугольник
нельзя построить, если хотя бы один из этих отрезков больше или равен сумме
двух других. Чтобы треугольник с заданными длинами сторон существовал,
необходимо, чтобы было выполнено три неравенства: a<b+c, b<a+c и c<b+a , но
необязательно проверять справедливость всех трех неравенств. Достаточно
проверить только одно (какое? как выбрать нужное неравенство?), остальные
будут выполнены автоматически.
Равнобедренные треугольники.
а) В равнобедренном треугольнике длины двух сторон равны 3см и 7см.
Чему равна длина третьей стороны?
б) Найдите стороны равнобедренного треугольника, если у него одна
сторона меньше другой на 4, а периметр равен 16.
2.
Расстояние по воздуху, как и все расстояния в этой задаче, от Шалона до
Витри 30км, от Витри до Шомона 80км, от Шомона до Сэн-Кантэна 236км, от
Сэн-Кантэна до Ремса 86км, от Ремса до Шалона 40км. Каково расстояние от
Ремса до Шомона?
3.
Домики Винни-Пуха, Пятачка, Кролика и Совы расположены на окружности.
Где нужно построить домик для ослика Иа, чтобы сумма расстояний от него до
домиков была минимальной ?
4.
Турист хочет дойти от палатки до костра, набрав по дороге в речке ведро
воды. Считая положения палатки и костра заданными, а берег реки прямым,
придумайте, как ему идти, чтобы путь был самым коротким.
5.
Верно ли, что среди любых ста отрезков можно выбрать три, из которых
можно составить треугольник?
6.
В. треугольнике длины двух сторон равны 3, 14 и 0, 67. Найдите длину
третьей стороны, если известно, что она является целым числом.
7.
Чему равна площадь треугольника со сторонами 18, 17, 35?
8.
Точка O лежит внутри треугольника ABC. Докажите, что AO+OC<AB+BC.
9.
В результате измерения четырёх сторон и одной из диагоналей некоторого
четырёхугольника получились числа: 1; 2; 2,8; 5; 7,5. Чему равна длина
измеренной диагонали?
1.