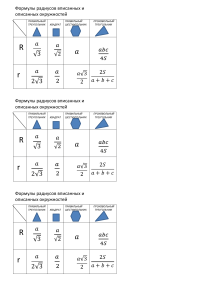
Калашникова София 8а ТФТЛ В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Дано: треугольник АВС, ∠С=90° Док-ть: a²+b²=c² Док-во: 1)Треугольник ABC, где ∠С=90°, повернем на C b a 90° градусов так чтобы он занял положение A'CB‘. 2)Проведём высоту B‘D 3)Рассмотрим четырёхугольник A‘АB‘В. Его можно разложить на равнобедренные треугольника САA' и СВВ‘, где ∠A'СА = ∠ВСВ' =90°. SCAA'=b²/2 => SCBB'=a²/2 SA'AB'B=(a²+b²)/2 4)Рассмотрим треугольники A'В'А и A'В'В. Они имеют общее основание A'B‘=с и высоты DA и DB, поэтому: SA'AB'B = c*DA/2+ c*DB/2 = c(DA+DB)/2 = c²/2 C b 5) Так как SA'AB'B=(a²+b²)/2 и SA'AB'B=c²/2, то (a²+b²)/2 = c²/2 a²+b²=c² a ч. т. д.