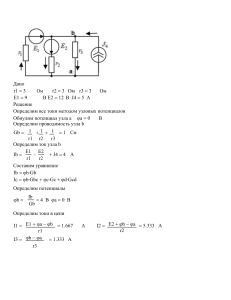
Волков В.А. ИОДО-325 Вариант 1522 Задача №5 Условие задачи. Для поперечного сечения (рис. 1) определить положение главных центральных осей и величины соответствующих главных моментов инерции. Исходные данные. ℎ⁄ 5 ⁄ 1 , мм 5 № схемы II ⁄ 5 Рис. 1. Заданная схема Дано: 5 мм; ℎ 5 25 мм; 5 мм; 5 25 мм; № схемы ‒II. Решение. 1. По исходным данным вычертим поперечное сечение в масштабе 1:1. 2. Составное сечение разобьем на 4 простые фигуры: 1) прямоугольник (основная площадь) с размерами: ширина 2 высота ℎ 2ℎ 50 мм; 25 50 75 мм 2) прямоугольник (дополнительная площадь) с размерами: ширина 3 высота ℎ 25 мм; 25 мм. 4) круг (дополнительная площадь) с диаметром 25 мм. 1 3. Проведем прямоугольную систему координат ′0 ′. Отметим на чертеже сечения центры тяжести каждой простой фигуры C1, C2, C3. 4. Определим координаты центров тяжести ( 25 мм; d 2 ) каждой простой фигуры: 12,5 мм; 2 − − 2 "# $ d , 32,5 мм; 37,5 мм; 12,5 мм; 2 2h − d 50 мм; 5. Определим положение центра тяжести сечения. Площади простых фигур: & ' & & 2ℎ) · 2 · π 2 4 3750 мм2 . 625 мм2 . 490,87 мм2 . Площадь всего сечения & & −& −& 2634,1 мм2 . Координаты центра тяжести всего сечения: & − & − & & & − & − & & 26,568 мм; 41,102 мм. 6. Отметим на чертеже центр тяжести «С» сечения с координатами ( С , С ). Проведем через центры тяжести простых фигур центральные оси , , параллельные осям , . 7. Определим моменты инерции простых фигур относительно их центральных осей. 2 Для прямоугольника 1): ./ .2 ℎ 12 50 ∙ 75 1,758 · 106 мм4 1,758 · 10 см4 ; 12 ℎ 50 ∙ 75 7,813 · 103 мм4 78,13 см4 ; 12 12 ./ 2 0. Для прямоугольника 2): ℎ 12 ./ 32552,1 мм 4 .2 ./ Для круга 3): 4 5 64 ./ 4255 64 ./ 3,2552 см 0. 2 1,9175 · 105 мм4 ./ 1,9175 см4 ; ./ .2 25 · 253 12 4 0. 2 8. Определим моменты инерции простых фигур относительно центральных осей сечения. Расстояния между параллельными центральными осями: 6 6 – 6 – – − − − 25 − 26,568 12,5 − 26,568 32,5 − 26,568 37,5 − 41,102 12,5 − 41,102 50 − 41,102 −1,568 мм; −14,068 мм; 5,932 мм. −3,602 мм; −28,602 мм; 8,898 мм; Определим моменты инерции простых фигур относительно центральных осей и . Для прямоугольника 1): . . ./ / 2 . .2 /2 & 6 & 6 & 1,758 · 108 7,813 · 103 '−3,602) · 3750 '−1,568) · 3750 −3,602 · '−1,568) · 3750 Для прямоугольника 2): 3 1,807 · 108 мм4 ; 7,905 · 103 мм4 ; 2,119 · 105 мм4 . ./ / . & .2 2 . 6 & /2 Для круга 3): . ./ / . . 3,2552 · 105 1,9175 · 105 6 & 1,9175 · 105 6 /2 '−28,602) ∙ 625 '−14,068) ∙ 625 −28,602 · '−14,068) ∙ 625 & .2 2 3,2552 · 105 & 5,439 · 103 мм4 ; 1,563 · 103 мм4 ; 2,515 · 103 мм4 . 8,898 · 490,87 5,932 · 490,87 8,898 · 5,932 · 490,87 5,804 · 105 мм5 ; 3,645 · 105 мм5 ; 2,591 · 105 мм5 9. Определим осевые и центробежный моменты инерции всего сечения относительно его центральных осей и : ./ .2 ./2 . . . / 2 /2 −. −. −. / 2 −. −. /2 1,807 · 108 − 5,439 · 103 − 5,804 · 105 / 7,905 · 103 − 1,563 · 103 − 3,645 · 105 2 −. 2,119 · 105 − 2,515 · 103 − 2,591 · 105 /2 10. Определение положения главных осей инерции −2./2 · 103 ) 6: ;' ) 6: ;' −2 · '−2,562 ) ./ − .2 1,205 · 108 − 5,978 · 103 α 2 2 → >, ? − оси 1,205 · 108 −2,562 · 103 −2,562 · 103 40,18° 11. Определим главные моменты инерции сечения. Вначале определим экстремальные значения главных центральных моментов инерции сечений: ./ .2 1,205 · 108 − 5,978 · 103 ± 2 2 1 1,484 · 108 8 3 3 ± ∙ I'1,205 · 10 − 5,978 · 10 ) 4'−2,562 · 10 ) мм5 ; J 2 3,189 · 103 Определим, какое значение (максимальное или минимальное) будет у главного момента инерции, взятого относительно главной оси >, расположенной под углом α к центральной оси . Для этого определим знак выражения .BCD 1 EF./ − .2 G 2 2 ∙ F./ − .2 G − cos 2O .K α 4./2 −7,247 · 10 8 .K > .Q .BCD .BRS 12. Выполним проверку проведенных вычислений: .T .T ./ .BCD .2 .BRS 1,205 · 108 1,484 · 108 5,978 · 103 3,189 · 103 4 1,484 · 108 мм5 3,189 · 103 мм5 1,802 · 108 ; 1,802 · 108 .