Учебная презентация (геометрические характеристики сечений)

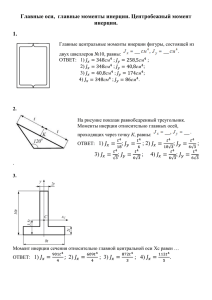
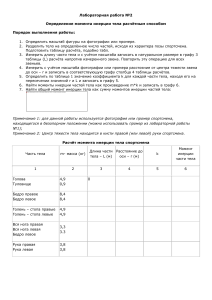
Геометрические характеристики
плоских сечений
Прочность при растяжении-сжатии зависит
от площади поперечного сечения А. Т.о. А –
геометрическая характеристика,
определяющая напряжения при
растяжении-сжатии. При изгибе, кручении
ситуация иная. Там напряжения зависят от
других характеристик поперечных сечений
стержней.
Пример
1
2
 2 > 1
z
Введем понятие статического момента:
y
dА

z
S y   zdA
A
S z   ydA
[см3]
A
Из теоретической механики известно:
y
Sz
Yc 
A
Zc 
Sy
A
Т.о. статические моменты относительно осей, проходящих через
центр тяжести сечения, равны нулю.
Оси, проходящие через центр тяжести, называются центральными
Введем понятие осевого момента инерции сечения:
I z   y 2 dA
A
I y   z 2 dA
[см4]
A
Центробежный момент инерции:
I zy   yzdA
A
Полярный момент инерции:
I     2 dA
A
Из рис. следует:
I     2 dA   ( z 2  y 2 )dA   z 2 dA   y 2 dA  I y  I z
A
A
A
I  I y  Iz
A
Моменты инерции простейших фигур
1. Прямоугольник
y
dA  b  dy

h
2
3
by
I z   y 2 da   y 2bdy 
dy
3
h
A

y
z
h
0
2
3
3
3
bh


b h h
    
12
3 8 8 
Рассуждая аналогично:
b
hb 3
Iy 
12
h
2
h

2

2. Треугольник
Оси z, y – центральные.
y
Из подобия треугольников:
2/3h
dy
y
by
0
1/3h
b
z
h
2

 h  y
3
  h;
by
b
2

 h  y b
3
 ;
by  
h
b2

dA  by dy   h  y dy;
h3

2. Треугольник
2
h
3
b 22
b 3
b 2

I z   y dA   y  h  y dy   y hdy   y dy 
h
3
h
h 3

h
A
2
2

3 2
h
3
1
 h
3
b2 y

h
h3 3
3
b y4

h 4
2
h
3
1
 h
3
2  8 3 1 3  b 16 4 1 4 
 b h  h    h  h  
9  27
27  4h  81
81 
bh 3
 ..... 
36
bh 3
Iz 
36
y
3. Круг
d
Ранее было:
I  I y  Iz
Iy  Iz 
2
dA  2d
z
R
I

R
I     2 dA   23d  2
A
0
Iy  Iz 
4
4
R
0
d 4
64
R 4
d

 R
2
2

d 4
32
4. Кольцо
y
I 


R
2
4
 r4

r
z
R
I y  Iz 
I
2



R
4
4
 r4

Моменты инерции относительно // осей
y
b
yС
dA
z
I z c , I y c , a, b
Определить:
z0
y0
zС
С
y
0
Дано:
I z , I y , I zy
I z c   y dA;
2
0
A
I y c   z02 dA;
a
A
z
I zc yc   y0 z0 dA;
A
I z    y0  a  dA   y02 dA  2a  y0 dA  a 2  dA
2
A
A
A
A
Статический момент = 0
относительно центральной оси
2
I

I

b
A
Аналогично:
y
yc
I z  I zc  a A
2
I zy   yzdA 
z  z0  b
y  y0  a
A
  z0  b  y0  a dA 
A
  z0 y0 dA  ab dA  b y 0 dA  a  z0 dA;
A
A
A
I zy  I zc yc  abA 
A
Последнее слагаемое м.б. > 0,  0.
Пример
Ранее было получено:
y
bh 3
Iz 
12
2
z
h
0
h
I z  I z c    bh 
2
bh 3 bh 3 bh 3



12
4
3
z1
b
bh 3
I z1 
3
Теорема
Центробежный момент инерции
Izy = 0, если одна из осей
является осью симметрии
сечения (фигуры).
y
dA
dA
I zy   yzdA 
A
y
y

z
A
пр
2
пр
ydA 
z
лев
A
лев
2
 z лев   zправ  0
-z
z
z
ydA 