SUPER

Оглавление
Введение ............................................................................................................................................... 2
1. Выборка и ее характеристики ......................................................................................................... 3
1.1. Эмпирическая функция распределения................................................................................... 3
1.2. Эмпирические (выборочные) моменты ................................................................................... 6
1.3. Примеры решения задач ........................................................................................................... 9
2. Теория точечных оценок ............................................................................................................... 14
2.1. Несмещенные оценки с минимальной дисперсией .............................................................. 14
2.2. Единственность Н.О.М.Д........................................................................................................ 17
2.3. Информационное количество Фишера .................................................................................. 18
2.4. Неравенство Крамера-Рао ....................................................................................................... 20
2.5. Эффективные оценки .............................................................................................................. 20
2.6. Экспоненциальное семейство распределений ...................................................................... 23
2.7. Улучшение неравенства Крамера – Рао. Неравенство Баттачария .................................... 24
2.8. Многомерный аналог неравенства Крамера−Рао ................................................................. 25
3. Методы нахождения оценок ......................................................................................................... 26
3.1. Оценки максимального правдоподобия ................................................................................ 26
3.2. Состоятельность оценки максимального правдоподобия ................................................... 29
3.3. Метод моментов ...................................................................................................................... 29
3.4. Примеры решения задач ......................................................................................................... 30
ПРИЛОЖЕНИЕ 1 ............................................................................................................................... 35
ПРИЛОЖЕНИЕ 2 ............................................................................................................................... 37
ПРИЛОЖЕНИЕ 3 ............................................................................................................................... 38
ПРИЛОЖЕНИЕ 4 ............................................................................................................................... 39
Список литературы ............................................................................................................................ 40
2
Введение
В методических указаниях излагаются основы математической статистики в
соответствии с программой этого курса для технических и экономических специальностей
вузов. Изложение ведется в строгой, но доступной пониманию форме. Основные понятия
иллюстрируются различными примерами практического содержания. В методических
указаниях достаточно полно освещены основные положения математической статистики в
соответствии с программой, утвержденной Минобразованием. Оно предназначено для
студентов технических и экономических специальностей вузов. Методические указания
посвящены математической статистике и некоторым ее применениям в технике и экономике и
в других исследованиях. В ней изложены основы выборочного метода, теории оценивания
вероятностных параметров.
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
3
1. Выборка и ее характеристики
1.1. Эмпирическая функция распределения
Исходным
материалом
для
всякого
статистического
исследования
служит
совокупность из n наблюдений, в результате которых случайная величина X приняла
значение x1 , , xn . В дальнейшем предполагаем, что испытания взаимно независимы и
произведены в неизменных условиях. Функция распределения F ( x) случайной величины X
неизвестна.
Известно лишь, что F ( x) принадлежит некоторому классу распределений Θ .
Набор наблюдений
x1 , , xn
называется повторной выборкой объема
n
из
совокупности Θ (или просто выборкой, если ясно о чем идет речь). При решении
статистических задач будем использовать различные функции от наблюдений.
Определение. Любая функция от результатов наблюдения называется статистикой.
Если статистика используется (или хотя бы претендует на использование) для
оценивания, то о ней говорят как об оценке.
Рассмотрим
выборку
x1 , , xn .
Перегруппировав
элементы
выборки
путем
расстановки их в возрастающем порядке так, что
x(1) ≤ x(2) ≤  ≤ x( n ) ,
получим упорядоченную выборку, которая называется вариационным (или статистическим)
рядом; величины x(i ) называют порядковыми статистиками.
Обозначим ν n ( x) ─ число выборочных значений не превосходящих x .
Функция
частоту события
*
F=
n ( x)
{ X < x}
ν n ( x)
=
n
число тех
, xi для которых
n
xi < x
представляет
в последовательности n наблюдений. Ее называют эмпирической
функцией распределения выборки.
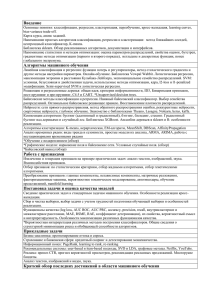
График функции распределения имеет вид (рисунок 1).
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
4
Рисунок 1 – График функции распределения
Эмпирическая функция распределения обладает всеми свойствами распределения:
1) 0 ≤ Fn* ( x) ≤ 1,
2) Fn* ( x) – неубывающая кусочно-постоянная функция.
Она является естественной оценкой теоретической функции распределения F ( x) (но
не совпадает с последней). Если все xi различны, то скачки эмпирической функции
распределения равны
1
j
и F ( x( j ) ) = . В общем случае скачок функции Fn* ( x) в точке x(i )
n
n
равен
хi ,
n j число тех
=
n
для которых xi = x j
n
j 1, n − 1 .
,=
Покажем, что при n → ∞, Fn* ( x) сходится по вероятности к F .
Теорема 1. Для õ∈ R и любого ε > 0 .
lim P( Fn* ( x) − F ( x) < ε ) =
1.
n →∞
Теорема Гливенко. Пусть F ( x) ─ функция распределения случайной величины X и
Fn* ( x) - эмпирическая функция распределения результатов n независимых наблюдений над
величиной X . Тогда при n → ∞
P  sup Fn* ( x) − F ( x) → 0  =
1.
 −∞< x <∞

(1.1)
Видим, что эта теорема устанавливает сходимость с вероятностью 1.
Теорема Гливенко устанавливает важный факт сближения эмпирической функции
распределения с теоретической, но не устанавливает, с какими вероятностями могут
возникать те или иные уклонения. Возникает задача определения функции распределения
величины
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
5
=
Dn
sup Fn* ( x) − F ( x) .
−∞< x <∞
Решение этой задачи было дано в 1933 г. Колмогоровым в виде следующей теоремы.
Теорема Колмогорова. Если F ( x) непрерывна, то при n → ∞
0, z ≤ 0;
 ∞
P{ nDn < z} → k ( z ) =

k −2 k 2 z 2
(
−
1)
e
, z > 0.
∑

 k = −∞
(1.2)
Теорема Колмогорова позволяет указать границы, в которых с большой вероятностью
будет заключена неизвестная функция распределения F ( x) . Если Zα подобрано так, что
1 − k ( Zα ) =
α , то неравенство
Fn* ( x) −
Zα
Z
< F ( x) < Fn* ( x) + α
n
n
выполняется сразу для всех x с вероятностью, близкой к 1 − α . Действительно,
=
P( nD
P( n sup Fn* ( x) − F=
( x ) < Zα )
n < Zα )
=∀
P( x : Fn* ( x) −
Zα
Z
< F ( x) < Fn* ( x) + α ) ≈ k ( Zα ) =
1− α.
n
n
В случае, когда объем выборки очень велик, выборочные значения часто подвергают
группировке. Область возможных значений случайной величины (СВ) разделяют на N
непересекающихся интервалов и объединяют выборочные значения, попадающие в один и тот
же интервал, при этом считают все выборочные значения, попавшие в данный интервал,
равными середине интервала.
Статистическим аналогом плотности распределения непрерывной СВ X может
служить гистограмма, которая строится по выборке x1 , , xn следующим образом. Интервал
I , содержащий наблюдения, разбивают на N (обычно равных) интервалов hi и полагают при
õ ∈ hi
pn∗ ( x ) =
График
"эмпирической
число тех i, для которых xi ∈ hi
.
nhi
плотности"
pn∗ ( x)
обычно
называют
гистограммой.
Основанием для введения такой оценки служат приближенное равенство
P( x ∈
=
hi )
∫ p( x)dx ≈ p( x)h ,
i
hi
справедливое для õ ∈ hi и малых hi .
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
6
1.2. Эмпирические (выборочные) моменты
Эмпирическая функция распределения содержит всю статистическую информацию,
которая накоплена в процессе извлечения выборки. Статистические свойства выборки можно
характеризовать не только эмпирической функцией распределения (ФР), но и более грубо ─
выборочными моментами. Выборочные моменты будем обозначать звездочкой (в отличие от
моментов СВ).
Выборочный момент k -го порядка определяется по формуле
1 n k
∑ xi ,
n 1
àk* =
(1.3)
т.е. он равен среднему арифметическому k -x степеней выборочных значений.
Выборочный момент первого порядка
à1*= x=
1 n
∑ xi
n 1
(1.4)
называется выборочным средним.
Выборочные моменты k -го порядка служат оценкой моментов k -го порядка СВ X .
Аналогично оценкой k -го центрального момента =
α k M( X − MX ) k служат выборочные
моменты
=
α k*
1 n
∑ ( xi − x)k .
n 1
(1.5)
В случае k = 2 , получаем выборочную дисперсию
*
2
α=
s=
2
1 n
( xi − x) 2 .
∑
n 1
(1.6)
Выборочное среднее характеризует расположение выборки на действительной
прямой; выборочная дисперсия является мерой рассеяния выборочных значений относительно
среднего. Можно показать, что при достаточно общих ограничениях на неизвестную функцию
распределения F ( x) выборочные моменты близки к соответствующим теоретическим
характеристикам F ( x) :
; α k M( X − MX ) k .
α k = MÕ k =
Найдем сначала математическое ожидание и дисперсию выборочных моментов. Так
как xk – независимы и распределены так же, как и X , то:
M
=
x
1 n
xk M
=
X a1 ,
∑ M=
n 1
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
(1.7)
7
1
Dx
=
n2
Таким образом, M x = a1 , D x =
α2
n
DX α 2
.
=
n
n
n
x
∑ D=
k
1
(1.8)
.
Аналогично находим,
a2 k − ak2
Ma = ak , Da =
.
n
*
k
*
k
(1.9)
Действительно:
1
1
M
=
xik
=
xik M
=
x k ak ,
∑
∑
n
n
1
1
1
1
Dak* =
D ∑ xik =2 ∑ Dxik = DX k = (MX 2 k − (MX k ) 2 ) =
n
n
n
n
1
=
(a2 k − ak2 ).
n
M
=
ak* M
Несколько
сложнее
вычисляются
математическое
ожидание
и
дисперсии
центральных выборочных моментов. Ограничимся вычислением MS 2 и DS 2 .
2
=
S
1 n
)2
∑ ( xk − x=
n 1
(1)
1
)2
∑ ( yk − y=
n
(2)
2
1
yk2 − y .
∑
n
(1.10)
1 n
yk =
xk − Mxk , y =
∑ yi ,
n 1
n
1
∑1 ( yk − y=) ∑ ( xk − Mxk − n ∑ ( xk + Mxk ))=2
n
n
1
1
= ∑ ( xk − ∑ xk − (Mxk − Mxk )) 2 = ∑ ( xk − x) 2 .
n
n
1
1
n
2
1
1
( yk − y=
)2
( yk2 − 2 yk y + y=
)
∑
∑
n 1
n
2
2
1
2
1 2
1
yk2 − y ∑ yk + y =
n
yk2 − 2 y + y .
=
∑
∑
n
n
n
n
Так как
Myk = M( X k − MX k ) = 0,
Myk2 =M( X k − MX k ) 2 =α 2 ,
M=
yk yl Myk=
Myl 0, (k ≠ l ), òî
2
=
My
α2
1 n
=
Myk yl
.
2 ∑
n k ,l =1
n
Из последней формулы и (1.10) находим, что
2
M S =α 2 −
α2
n
=
n −1
α2.
n
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
(1.11)
8
В формуле (1.11) правая часть смещена относительно α 2 . Если вместо S
2
ввести
величину
n 2
1 n
=
S
∑ ( xk − x)2 ,
n −1
n −1 1
2
=
S1
2
то для нее получим MS 1 = α 2 .
2
Перейдем к вычислению DS . Из (1.10) находим
2
21
1  n

 4
S = 2  ∑ yk2  − 2 y  ∑ yk2  + y .
n  1
n


4
(1.12)
Так как случайные величины yk , k = 1 n независимы и Myk = 0 , то в правой части
равенства
4
My =
1
n4
n
∑
l1 , l2 , l3 , l4 =1
Myl yl yl yl
1
2
3
4
4
2 2
отличны от нуля только слагаемые M y = α 4 (их n ) и слагаемые My=
α l2 , l ≠ k (которых
l yk
Cn2=
C42 3n(n − 1) ). Поэтому
4
My =
α 4 + 3(n − 1)α 22
n3
.
 ( y 2 )2 
∑ k  = n2 M  1 y 2 ( y 2 )  = α + (n − 1)α 2 .
Аналогично находим nM 
∑ k  4
2



n
n


2
4
2
Отсюда и из (1.12) по формуле D
=
S
M S − (M S ) 2 получаем
2
α 4 − α 22 2(α 4 − 2α 22 ) α 4 − 3α 22
DS =
.
−
+
n
n2
n3
 1 
1
*
Можно показать, что Mα=
αν + k   , M(αν* − αν ) k =
k k .
ν
n 
n
Теорема. Если конечен теоретический момент a2k , то выборочный момент k -го
*
порядка a2k
сходится по вероятности, когда размер выборки неограниченно возрастает к
соответствующему k -му моменту исходного распределения.
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
9
1.3. Примеры решения задач
Задача №1.
Вычислить несмещенные оценки среднего значения µ , дисперсии σ 2 и стандартного
отклонения σ генеральной совокупности x , S 2 , S по выборкам (43, 51, 44, 47, 34) и (52, 42,
40, 38, 37).
Решение:
Для нахождения x , S 2 , S используем формулы:
x=
=
S2
1 n
∑ xi ,
n i =1
1 n
( xi − x) 2 ,
∑
n − 1 i =1
S = S2 .
Вычисления сумм оформим в таблицы 1 и 2.
Таблица1
Таблица2
i
xi
xi − x
( xi − x) 2
i
xi
xi − x
( xi − x) 2
1
2
3
4
5
52
42
40
38
37
10.2
0.2
-1.8
-3.8
-4.8
104.04
0.04
3.24
14.44
23.04
1
2
3
4
5
43
51
44
47
34
-0.8
7.2
0.2
3.2
-9.8
0.64
51.84
0.04
10.24
96.04
209
–––
144.8
219
–––
158.8
∑
x=
S2 =
219
= 43.8,
5
158.8
= 31.76,
5
S = 31.76 = 5.64,
∑
x=
S2 =
209
= 41.8,
5
148.8
= 29.76,
5
S = 29.76 = 5.45.
Задача №2
Вычислить несмещенные оценки параметров генеральной совокупности x , S 2 , S по
трем выборкам: x =(82, 70, 83, 80, 76, 81, 80, 76, 70, 79, 74, 77, 65, 80, 79), y =(-237, -209, -243,
-239, -221, -238, -238, -223, -207, -237, -216, -228, -193, -234, -229), z =(730, 626, 737, 716, 681,
721, 710, 680, 626, 708, 658, 690, 579, 714, 704).
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
10
Решение:
Выборки содержат мало повторяющихся элементов, поэтому вариационный ряд мы
составлять не будем. При вычислении можно использовать те же формулы, что и в примере 1,
или использовать следующие:
=
x
1 n
∑ ( xi − c) + c,
n i =1
1 n
( xi − c) 2 − ( x − c) 2 ,
∑
n i =1
2
n
S2 =
S .
n −1
Промежуточные вычисления сведены в таблицу 3.
2
=
S
Таблица3
xi
xi − cx
( xi − cx ) 2
yi
yi − c y
( yi − c y ) 2
zi
zi − cz
( zi − cz ) 2
82
70
83
80
76
81
80
76
70
79
74
77
65
80
79
8
-4
9
6
2
7
6
2
-4
5
0
3
-9
6
5
64
16
81
36
4
49
36
4
16
25
0
9
81
36
25
-237
-209
-243
-239
-221
-238
-238
-223
-207
-237
-216
-228
-193
-234
-229
-19
9
-25
-21
-3
-20
-20
-5
11
-19
2
-10
25
-16
-11
361
81
625
441
9
400
400
25
121
361
4
100
625
256
121
730
626
737
716
681
721
710
680
626
708
658
690
579
714
704
72
-32
79
58
23
63
52
21
-32
50
0
22
-79
56
46
5184
1024
6241
3364
529
3969
2704
441
1024
2500
0
484
6241
3136
2116
42
482
-122
3930
399
38957
∑
∑
xmin =65, xmax =83.
ymin =-243, ymax =-193.
Возьмем cx =74.
x=
∑
zmin =579, zmax =737.
Возьмем c y =-218.
42
+ 74 = 76.8 .
15
2
Sx =
−122
y = − 218 =
−226.13 .
15
Возьмем cz =658.
z=
399
+ 658 = 684.6 .
15
482
− (76.8 − 74) 2 = 32.13 − 7.84 = 24.29,
15
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
11
15
24.29 26.03,
=
14
26.03 5.1,
Sx =
=
S x2
=
3930
2
− ( −226.13 + 218 )= 262 − 66.15
= 195.85,
15
15
195.85 209.83,
S y2 =
=
14
209.83 14.49,
Sy =
=
2
S=
y
38957
2
− ( 684.6 − 658 ) = 2597.13 − 707.56 = 1889.57,
15
15
1889.57 2024.53,
S z2 =
=
14
2024.53 44.99.
Sz =
=
2
Sz =
Задача №3.
Вычислить несмещенные оценки параметров генеральной совокупности x , S 2 , S по
выборке (67, 68, 70, 76, 80, 87, 75, 79, 79, 73, 86, 78, 79, 67, 79, 82, 70, 83, 80, 76, 81, 80, 76, 70,
79, 74, 77, 65, 80, 79, 78, 75, 82, 85, 68, 72, 71, 72, 68, 86, 85, 71, 72, 76, 90, 95, 88, 86, 71, 87, 77,
73, 82, 74, 67, 82, 72, 74). Сначала составить вариационный ряд.
Решение:
Найдем xmin = 65 и xmax = 95 . Выберем началом первого интервала 65, а длиной
интервала - 5. Вычисления проводим по формулам:
1 n
1  m ( xi − c) 
(
)
−
+
≡
x
c
c
ni  k + c,
∑ i
∑
n i 1=
n  i 1 k
=

=
x
 xi − c 
∑

 ni
2
k 
i =1 
=
S
k 2 − ( x − c) 2 ,
n
2
m
где k ─ длина интервала, ni ─ количество попавших в i -тый интервал элементов выборки, c
─ произвольное число.
S2 =
2
n
S .
n −1
Промежуточные вычисления представлены в таблице 4.
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
12
Таблица4
Середина
интервала, xi
2
2
xi − c
xi − c
xi − c 
 xi − c 

Интервал
ni 
 ni


k
k
 k 
 k 
65-70
10
67.5
-2
-20
4
40
70-75
14
72.5
-1
-14
1
14
75-80
18
77.5
0
0
0
0
80-85
8
82.5
1
8
1
18
85-90
7
87.5
2
14
4
28
90-95
1
92.5
3
3
9
9
109
58
–––
–––
-9
–––
∑
Выберем c из середины интервала, в который вошло больше всего элементов, то есть
ni
c =77.5, k =5.
−9
x = ⋅ 5 + 77.5 =
76.7,
58
58
S 2 = ⋅ 46.36 =
47.17,
57
2
109
S = ⋅ 25 − (76.7 − 77.5) 2 =47 − 0.64 =46.36,
58
S =47.17 =
6.86.
Задача №4.
Вычислить несмещенные оценки параметров генеральной совокупности x , S 2 , S по
выборкам А и В, используя результаты, полученные в примере 3.
Выборка А: 0 4 2 0 5 1 1 3 0 2 2 4 3 2 3 3 0 4 5 1 3 1 5 2 0 2 2 3 2 2 2 6 2 1 3 1 3 1 5 4 5 5
3 2 2 0 2 1 1 3 2 3 5 3 5 2 5 2 1 1 2 3 4 3 2 3 2 4 2.
N=69.
Начало первого интервала: 0.
Длина интервала: 1.
Выборка В: 135 133 124 132 104 152 134 130 129 120 122 124 117 123 123 129 121 122
125 131 147 124 137 112 126 128 111 129 115 147 131 132 137 119 125 120 129 125 123 127 132
118 133 132 132 134 131 120 135 132 125 132 108 114 121 133 133 135 131 125 114 115 122 131
125 132 120 126 115 117 118 118 132 134 127 127 124 135 128 127 115 144 129 120 137 127 125
116 132 120 117 127 118 109 127 122 120 135 116 118 133 136 125 126 119 126 129 127 129 124
127 132 126 131 127 130 126 124 135 127 124 123 123 130 132 143 122 138 120 134 108 132 121
111 123 140 137 120 125 131 118 120 120 136 129 127 116 138 128 133 122 131 128 140 138 134
120 126 109 137 111 115 117 130 113 126 115 124 125 118 115 128 123 129 128 120 115 134 118
135 134.
N=181.
Начало первого интервала: 102.
Длина интервала: 4.
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
13
Решение:
Для нахождения x , S 2 , S используем формулы:
m
=
x
∑
i =1
xi − c
ni
k
k +c;
n
 xi − c 
∑

 ni
k 
2
i =1 
=
S
k 2 − ( x − c) 2 ;
n
2
m
S2 =
n
S2.
n −1
Для выборки А имеем:
x = 2.51,
S 2 = 2.2072,
n =69,
S2 =
69
⋅ 2.2072 = 2.2396.
68
Для выборки В имеем:
x = 126.02
S 2 = 65.9774,
n =181,
S2 =
181
⋅ 65.9774 = 66.3440.
180
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
14
2. Теория точечных оценок
2.1. Несмещенные оценки с минимальной дисперсией
Предположим, что о распределении СВ
X
известно, что оно принадлежит
некоторому параметрическому семейству распределений. В случае непрерывной СВ это
означает, что известен вид плотности p ( x | θ ) , но неизвестно значение параметра θ ,
определяющего конкретную плотность. Параметр θ может быть вектором. Например, для
нормального распределения θ = ( µ , σ )
=
p( x | θ )
1
exp{−( x − µ ) 2 / 2σ 2 }.
σ 2π
В случае дискретной СВ p ( x | θ ) будет обозначать вероятность P( X = x) . Например,
для пуассоновского распределения
p ( x=
|θ )
θx
x!
θ
e −=
, x 0,1, 2,3,  .
Пусть τ (θ ) – некоторый числовой параметр, представляющий для нас интерес.
Например, τ (θ ) = θ , τ ( µ , σ ) = µ , τ ( µ , σ ) = µ σ .
Рассмотрим
задачу
оценивания,
состоящую
в
построении
такой
функции
t = ( x1 , , xn ) , чтобы при подстановке вместо аргументов x1 , , xn данных выборки мы
получили числа, близкие к τ (θ ) . Такую близость можно обеспечить лишь в среднем. Поэтому
требования, предъявляемые к качеству оценок, формулируется в вероятностных терминах,
относящихся к распределению оценок, рассматриваемых как случайные величины. Это
требование, состоящее в том, чтобы значения оценки в большинстве опытов были близки к
значению оцениваемого параметра, можно сформулировать в виде следующего определения.
Определение. Оценка
t = ( x1 , , xn )
называется несмещенной для τ (θ ) , если
Mθ t ( x1 ,..., xn ) = τ (θ ) для всех θ , где Mθ – символ математического ожидания при условии,
что случайный вектор ( x1 , , xn ) имеет распределение L( x | θ ) = p ( x1 | θ )... p ( xn | θ ).
Например, как показано выше, x и S
2
─ несмещенные оценки для µ и σ 2
соответственно.
Но как правило, одно лишь требование несмещенности не выделяет оценку t ( x)
однозначно. Поэтому следующим желательным требованием является требование минимума
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
15
дисперсии этой оценки. Чтобы статистика могла служить хорошей оценкой данного
параметра τ (θ ) , необходимо, чтобы распределение этой статистики было сосредоточенно в
достаточной близости от неизвестного значения τ (θ ) , так, чтобы вероятность больших
отклонений этой статистики от τ (θ ) была достаточно мала. Тогда при систематическом
многократном применении этой статистики в качестве оценки данной характеристики в
среднем будет получаться достаточная точность. Вероятность больших отклонений будет
мала, и они будут встречаться редко. Таким образом, среди всех несмещенных оценок t ( x)
для τ (θ ) более желательной является та оценка, которая имеет минимальную дисперсию
Dθ=
(t ( x)) M(t ( x) − τ (θ )) 2 для всех θ .
Такие оценки называются несмещенными оценками с минимальной дисперсией
(Н.О.М.Д.).
Определение. Несмещенной оценкой с минимальной дисперсией называется такая
оценка t ∗ ( x1 , , xn ) , что Dt * ≤ Dt для всех θ , для любой несмещенной оценки t ( x1 , , xn )
параметра τ (θ ) . Уже эти требования, как правило, выделяют оценку t ( x) однозначно, если
такая оценка вообще существует. Существование же Н.О.М.Д. имеет место далеко не всегда,
так как дисперсия для этих оценок должна быть минимальной равномерно по θ . Это
обстоятельство является, пожалуй, самым серьезным аргументом против таких сильных
требований.
При
неограниченном
увеличении
числа
наблюдений,
т.е.
lim P( t ( x1 ,..., xn ) − τ (θ ) < ε ) =
1 для ∀ε > 0 .
n →∞
Итак, состоятельность оценки означает, что при достаточно большом количестве
наблюдений n со сколь угодно большой достоверностью отклонение оценки от истинного
значения параметра меньше любой наперед заданной величины.
Для того, чтобы несмещенная оценка была состоятельной, достаточно, чтобы
дисперсия оценки стремилась к нулю при n → ∞ (это следует из неравенства Чебышева).
Пример 1. Показать что оценки
а) x =
2
б) S
=
1 n
∑ xi - выборочное среднее,
n 1
1 n
∑ ( xi − x)2 - выборочная дисперсия,
n 1
являются состоятельными оценками.
Решение. По закону больших чисел
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
16
 n

 ∑ xi

− MX 1 < ε  → 1, n → ∞ ,т.е.
P 1
 n



оценка а) состоятельна, так как x =
2
б)=
S
1 n
∑ xi ;
n 1
2
2
1 n 2
1 n 2
(
2
)
x
−
x
x
+
x
=
xi − 2 x ∑ xi + nx=
∑
∑
i
i


n 1
n  1i

=
Первый
член
является
∑x
2
i
n
2
2
− 2 x + x=
средним
∑x
2
i
n
2
−x .
арифметическим
случайных
величин
xi2
следовательно, он сходится по вероятности к Mx12 , второй член сходится по вероятности
2
[ Mx1 ]2 . Это означает, что S по вероятности сходится к Mx12 − (Mx1 ) 2 =
Dx1 . Следовательно,
оценка является состоятельной, но она не является несмещенной.
Пример 2. (Существование нескольких несмещенных оценок).
x1 , , xn – независимые одинаково распределенные СВ, имеющие пуассоновское
распределение Pθ {x=
k=
}
1
2
Оценка
=
S1
θk
k!
e −θ .
1
( xi − x) 2 является несмещенной оценкой для дисперсии. Из того,
∑
n −1
что для пуассоновского распределения математическое ожидание и дисперсия равны θ и x
является несмещенной оценкой для θ следует, что x является несмещенной оценкой для
дисперсии θ . Кроме того, любая комбинация α x + (1 − α ) S12 является несмещенной оценкой
θ (α ∈ (−∞, ∞)) , т.е.
M(α x + (1 − α ) S12 ) = α M x + (1 − α )MS12 = αθ + (1 − α )θ = 0.
Однако оценка x имеет наименьшую дисперсию.
Пример 3. (когда не существует несмещенной оценки).
Производится одно наблюдение
x , где
x
– СВ, имеющая пуассоновское
распределение с неизвестным параметром θ
Pθ (=
x k=
)
θk
k!
e −θ , =
k 0,1, .
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
17
Показать, что для τ (θ ) =
1
не существует несмещенной оценки.
θ
Решение. Предположим, что t ( x)
является несмещенной оценкой τ (θ ) , т.е.
Mθ t ( x) = τ (θ ) , откуда
∞
t ( x)e −θ θ k 1
t ( x) k eθ 1 ∞ θ k
=
⇒ ∑
θ =
=
∑ .
θ
θ θ k 0 k!
k!
k!
0
=
k 0=
∞
∑
=
k
Окончательно
∞
t ( x) k
1
=
θ
θ k.
∑ k!
∑
k
(
1)!
+
k = −1
И как легко понять, не существует функции t ( x) , для которой последнее равенство
было бы справедливо для всех θ > 0 .
Пример 4. (когда несмещенная оценка абсурдна).
Случайная величина x имеет геометрическое распределение:
P{x = k} = q k p , k ≥ 0, p + q = 1
(число неудач, предшествующих первому успеху в последовательности испытаний Бернулли).
Несмещенной оценкой параметра p является оценка
1, x = 0,
t ( x) = 
0, x > 0.
Действительно,
∞
∑ t (k )q
k
p=
p,
∞
∑ t ( x)q
k
=
k 0=
k 0
1, k = 0,
=⇒
t (k ) =
1

0, k > 0.
Однако эта оценка абсурдна, т.к., например, если первый успех получен на втором
испытании, т.е. x = 1 , то абсурдно говорить, что вероятность успеха P = 0 .
2.2. Единственность Н.О.М.Д.
Докажем, что Н.О.М.Д. единственная в том смысле, что если t1 и t2 есть две
Н.О.М.Д. для τ (θ ) , то t1 = t2 с вероятностью единица.
В самом деле, рассмотрим новую оценку=
t3
1
(t1 + t2 ), для которой
2
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
18
M θ t3 =
Dt3=
1
(Mt1 + Mt2 ) = τ (θ ),
2
1
(Dt1 + Dt2 + 2 cov(t1 , t2 )).
4
Известно, что cov(t1 , t2 ) ≤ Dt1 Dt2 , причем знак равенства имеет место лишь тогда,
когда почти всюду
(t1 −=
τ ) k (θ )(t2 − τ ),
(2.1)
где k (θ ) ─ любая функция от θ . Если обозначить D
=
t1 D=
t2 V , то мы показали, что
cov(t1 , t2 ) ≤ V , а значит, Dt3 ≤ V , причем знак равенства имеет место, лишь когда выполнено
(2.1). Но, с другой стороны, t1 и t2 ─ Н.О.М.Д., т.е. =
V Dt1 ≤ Dt3 , поэтому Dt3 = V и
следовательно, выполнено (2.1).
Найдем k (θ ) . Имеем
=
=
V cov(
t1 , t2 ) k (θ )V , откуда k (θ ) = 1 и, значит, t1 = t2 почти
всюду.
2.3. Информационное количество Фишера
В дальнейшем мы будем предполагать, что неизвестный параметр θ принадлежит
открытому интервалу на прямой R . Множество X , для которых p ( x | θ ) ≠ 0 , не зависит от θ .
Эти условия, например, не выполняются для равномерного распределения на интервале (0, θ ) ,
где θ - неизвестный параметр, так как область, где p ( x | θ ) ≠ 0 , зависит от θ .
Пусть
X
– СВ с распределением
p ( x | θ ) . Количество информации о θ ,
содержащееся в случайной величине X , определяется по Фишеру как
 ∂ ln P 
 ∂ ln P 
I (θ ) M
Dθ 
,
=
=
θ 

 ∂θ 
 ∂θ 
2
 ∂ ln P 
т.к. Mθ 
= 0.
 ∂θ 
Действительно,
1 ⇒ ∫ p '( x | θ )dx =
0 ⇒
∫ p( x | θ )dx =
∫ p( x | θ )
p '( x | θ )
∂ ln P
 ∂ ln P 
dx =
0 ⇒ ∫
p ( x | θ )dx =
0 ⇒ Mθ 
0.
=
p( x | θ )
∂θ
 ∂θ 
Рассмотрим некоторые свойства информационного количества.
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
(2.2)
19
Свойство 1. Пусть I1 (θ ) и I 2 (θ ) ─ количества информации о θ содержащиеся в
независимых величинах
и
x1
x2
соответственно, а
I (θ )
количество информации,
содержащиеся в паре ( x1 , x2 ). Тогда I= I1 + I 2 .
Свойство 2. Пусть x1 , , xn – независимые одинаково распределенные величины и I
─ количество информации о θ , содержащейся в каждой из них. Тогда количество
информации в ( x1 , , xn ) равно nI .
Приведем эквивалентную форму количества информации. Легко видеть, что
1 ⇒ ∫ p '( x | θ )dx =
0 ⇒ ∫ p ''( x | θ )dx =
0.
∫ p ( x | θ )dx =
1
Далее,
∂2
∂  p '( x | θ )  p ( x | θ ) ⋅ p "( x | θ ) − ( p '( x | θ )) 2
=
=
=
ln
(
|
)
p
x
θ
∂θ 2
∂θ  p ( x | θ ) 
( p ( x | θ )) 2
2
p "( x | θ )  p '( x | θ ) 
.
=
−
p ( x | θ )  p ( x | θ ) 
 ∂2

Поэтому M  2 =
ln p ( x | θ ) 
∂ θ

∫ p "( x | θ )dx − I (θ ) , то есть
 ∂2

I (θ ) = −M  2 ln p ( x | θ )  .
 ∂θ

(2.3)
Во многих случаях использование последней формулы приводит к более простым
выкладкам.
Пример 1. Распределение Бернулли. Положим, что X имеет распределение Бернулли,
параметр которого θ неизвестен (0< θ <1). Определим количество информации I (θ ) о θ ,
содержащейся
в
X.
Так
как
X
принимает
два
значения
0
и
1,
то
ln p ( x | θ=
) x ln θ + (1 − x) ln(1 − θ ).
Так как MX = 0 , то информация по Фишеру
 ∂ 2 ln p ( x | θ )  θ
1−θ
1
1
1
=2 +
=+
=
I (θ ) =
M
.

2
2
∂θ
(1 − θ ) θ 1 − θ θ (1 − θ )

 θ
Пример 2. Нормальное распределение. Предположим, что X имеет нормальное
распределение с неизвестным средним µ и известной дисперсией σ 2 . Определим I ( µ )
СВ X :
1
( x − µ )2
2
ln=
p( x | µ )
ln 2πσ −
.
2
2σ 2
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
20
Следовательно,
получаем I ( µ ) =
1
σ2
∂ 2 ln p ( x | µ )
1
∂ ln p ( x | µ )
x−µ
= − 2 ; поэтому, учитывая (2.2),
= − 2 и
2
∂θ
∂θ
σ
σ
.
2.4. Неравенство Крамера-Рао
Если
x1 , , xn
– выборка, то плотность распределения СВ ( x1 , , xn ) равна
L( x1 ,..., xn | θ ) = p1 ( x1 | θ )... pn ( xn | θ ).
Для функции L Фишером предложен термин “функция правдоподобия”. (Если
рассматривать ее, как функцию от θ при фиксированном x ). Пусть θ - числовой параметр.
 ∂ ln L 
Величина I = Mθ 
 называется количеством информации (по Фишеру), содержащейся в
 ∂θ 
2
выборке.
Теорема 1. Неравенство Крамера-Рао.
Пусть t ( x) ─ несмещенная оценка для τ (θ ) . Тогда
Dθ t ≥
(τ '(θ )) 2
(τ '(θ )) 2
.
=
2
I
 ∂ ln L 
Mθ 

 ∂θ 
При этом знак равенства имеет место тогда и только тогда, когда
(2.4)
∂ ln L
имеет вид
∂θ
∂ ln L
= À(θ )(t ( x) − τ (θ )),
∂θ
где A(θ ) - некоторая функция, зависящая лишь от θ , t ( x) ─ несмещенная оценка для τ (θ ) ,
если Mθ t ( x1 ,..., xn ) = τ (θ ) для всех θ .
2.5. Эффективные оценки
Правая часть неравенства Крамера-Рао есть минимальная граница дисперсии для
каждого θ . Несмещенная оценка, для которых эта граница достигается, называются
эффективными оценками. Ясно, что эффективная оценка для τ (θ ) есть Н.О.М.Д. для τ (θ ) и,
значит, она единственна.
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
21
Теорема. Для того чтобы несмещенная оценка t = t ( x) для τ (θ ) была эффективной,
необходимо и достаточно, чтобы
∂ ln L
= À(θ )(t ( x) − τ (θ )),
∂θ
(2.5)
где À(θ ) ─ есть некоторая функция, зависящая лишь от θ . При этом
Dt =
τ '(θ )
.
A(θ )
(2.6)
Пример 1.
Показательное распределение =
p ( x | θ ) θ e −θ x , x > 0,
1.
=
L
n
eθ θ
∏θ =
− xi
∑ xi θ n e − nθ x ; =
e=
ln L n ln θ − nθ x ,
n −θ
i −1
∂ ln L n
1
=− nx =
− n( x − ),
∂θ
θ
θ
при τ (θ ) =
1
θ
; À = −n ; t = x получаем
∂ ln L
= À(t − τ (θ )).
∂θ
Следовательно, x ─ эффективная оценка для τ (θ ) =
1
θ
и=
Dx
2 .Пуассоновское распределение с параметром θ :=
p( x | θ )
τ '(θ )
1
.
=
A(θ ) nθ 2
θk
=
e −θ , x 0.2 .
k!
n
θ xi −θ  n 1  − nθ nx
=
e
∏ e θ ,
∏
1 xi ! 
i −1 xi !
 i=
=
L
∂ ln L
nx n
=−n +
= ( x − θ ),
∂θ
θ θ
при
A
=
τ '(θ ) θ
n
.
Dx =
, t x , τ=
(θ ) θ получаем, что x - эффективная оценка для θ и=
=
A(θ ) n
θ
3. Рассмотрим семейство распределений N (θ , σ 2 ) с известной дисперсией σ 2
p( x =
|θ )
В данном случае L( x1 ,...,=
xn | θ )
1
 1

exp  − 2 ( x − θ ) 2  .
σ 2π
 2σ

σn
(
∂ ln L 1
=
σ2
∂θ
1
2π
)
n
 1

exp  − 2 ( xi − θ ) 2  .
 2σ

∑ ( x − θ=)
i
n
σ2
(õ −θ ) .
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
22
∂ ln L
Последнее равенство совпадает с (2.5), если
= À(θ )(t ( x) − τ (θ )),
∂θ
n
A(θх)=
σ
2
, xt ( x)=
=
1
∑ i , τ (θ )= θ .
n
τ '(θ ) σ 2
Поэтому x есть Н.О.М.Д. для θ с дисперсией
.
Dt =
=
A(θ )
n
4. Рассмотрим семейство распределений N ( µ , θ 2 ) с известным средним µ .
В данном случае p ( x =
|θ )
=
L
1
 1

exp  − 2 ( x − µ ) 2  .
θ 2π
 2θ

1
θ
n
( 2π )
n /2
 1
exp  − 2
 2θ
∑ (x − µ)
i
2

.

n 1
n 1
∂ ln L

=
− + 3 ∑ ( xi − µ ) 2 = 3  ∑ ( xi − µ ) 2 − θ 2 )  .
∂θ
θ θ
θ n

∂ ln L
Это совпадает с (2.5), если
= À(θ )(t ( x) − τ (θ )),
∂θ
n
1
A(θ ) =3 , t ( x) = ∑ ( xi − µ ) 2 , τ (θ ) =
θ2 ,
n
θ
т.е.
t ( x)
=
1
( xi − µ ) 2 является несмещенной оценкой с минимальной дисперсией для θ 2 ,
∑
n
причем D
t ( x)
=
τ '(θ ) 2θ 4
.
=
A(θ )
n
5. Биноминальное распределение.
L(r | θ ) = Cnr ⋅ θ r ⋅ (1 − θ ) n − r , r = 0,1,..., n,
ln L= ln Cnr + r ln θ + (n − r ) ln(1 − θ ),
∂ ln L r n − r
n r

=−
=
 −θ .
∂θ
θ 1 − θ θ (1 − θ )  n

Таким образом, t =
r
есть Н.О.М.Д. для θ и
n
=
Dt
τ '(θ ) θ (1 − θ )
.
=
A(θ )
n
6. Для семейства распределений Коши.
p( x | θ ) =
1
1
.
π 1 + ( x − θ )2
Получаем
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
23
L ( x, θ ) =
1
π
n
n
1
∏ 1+ (x −θ )
1
2
,
i
ln L =
−n ln π − ∑ ln(1 + ( xi − θ ) 2 ),
n
xi − θ
∂ ln L
= 2∑
.
2
∂θ
1 1 + ( xi − θ )
Это равенство не может иметь форму (2.5), поэтому Н.О.М.Д. в этом случае не
существует.
Замечание 1. Из (2.5) видно, что если Н.О.М.Д. существует, то она существует лишь
для какой-то одной функции τ (θ ) параметра θ и не существует ни для какой другой функции
параметра θ .
2.6. Экспоненциальное семейство распределений
Для того, чтобы выполнялось соотношение
∂ ln L
= À(θ )(t ( x) − τ (θ )),
∂θ
необходимо и достаточно (при некоторых условиях гладкости), чтобы плотность P( x | θ )
имела вид
=
P ( x | θ ) exp{ A(θ ) B ( x) + C (θ )} .
Такое семейство распределений часто называют экспоненциальным семейством
распределений. Для этого семейства распределений Н. О. М. Д. Существует и равна
t ( x1 ,..., xn ) =
1 n
∑ B( xk ),
n 1
τ ' (θ )
C ' (θ )
; Dθ t =
.
τ (θ ) = − '
nA' (θ )
A (θ )
Действительно,
L( x1 ,...xn | θ ) = P( x1 | θ )...P( xn | θ ) ,
n
ln L( x1 ,..., xn | θ ) = ∑ ln P( xi | θ ) ,
1
∂ ln L
=
∂θ
n
(θ )
∑ A (θ ) B( x ) + nC=
'
i =1
'
i
nA' (θ )(
τ ' (θ )
1
C ' (θ )
.
B( xi ) + ' ) ; Dt =
∑
nA(θ )
n
A (θ )
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
24
2.7. Улучшение неравенства Крамера – Рао. Неравенство Баттачария
Можно найти лучшую (т.е. большую) нижнюю границу для дисперсии оценки, чем
правая часть, а неравенстве Крамера – Рао в случаях, когда последняя не достигается, т.е.
когда не существует эффективной оценки. Основное условие того, чтобы нижняя граница
дисперсии в неравенстве Крамера – Рао достигалась, состоит в существовании оценки t , для
которой t − τ (θ ) есть линейная (для каждого θ ) функция от
∂
1 ∂L
.
ln L =
∂θ
L ∂θ
Но даже если такая оценка не существует, может существовать оценка, для которой
t − τ (θ ) есть линейная функция от
1 ∂s L
1 ∂L 1 ∂ 2 L
.
,...,
;
L ∂θ s
L ∂θ L ∂θ 2
Именно этот факт приводит к следующим рассуждениям Баттачария (Bhattacharyya).
Положим
(k )
L
∂k L
dk
(k )
= k ; τ = k τ (θ ) .
∂θ
dθ
Теорема. Пусть t = t ( x) есть несмещенная оценка для τ (θ ) . Тогда
Dθ t ≥
где aij = Mθ (
s
∑cc a
i , j =1
i
j ij
,
(2.7)
L(i ) L( j )
) , i, j = 1,..., S , а коэффициенты ci = ci (θ ) определяются системой
L L
s
∑a
i =1
ij
= τ (i ) , i = 1, s .
(2.8)
Если матрица A = {aij } обратима и A−1 = {a ij } , то
Dθ t ≥
s
∑a τ
τ
ij ( i ) ( j )
.
(2.9)
i , j =1
Последнее неравенство есть неравенство Баттачария. Неравенства (2.7) и (2.9)
s
превращаются в равенство тогда и только тогда, когда t − τ (θ ) =
∑ ci
i =1
L(i )
при некоторых
L
ci = ci (θ ) .
Пример.
Рассмотрим нормальную модель N (θ , σ 2 ) . Здесь
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
25
)
L( x | θ
=
 1
exp − 2
n
( 2πσ )
 2σ
1
n
∑ (x −θ )
2
i
i =1

,

и можно проверить, что
1  2θσ 2 ∂L σ 4 ∂ 2 L 
σ2
2
+
=
−
−θ 2.
X
L  n ∂θ n 2 ∂θ 2 
n
∗
По критерию Баттачария отсюда следует, что статистика T=
X2 −
σ2
n
─ оптимальная
(то есть несмещенная с минимальной дисперсией) оценка для τ (θ ) = θ 2 .
2.8. Многомерный аналог неравенства Крамера−Рао
Будем предполагать, что θ = (θ1 ,..., θ r ) .
Теорема. Пусть t ( x) − несмещенная оценка для числовой функции τ (θ ) = τ (θ1 ,...,θ r ).
Тогда
Dθ t ≥
где aij = Mθ (
r
∑a cc
i , j =1
ij i
j
,
(2.10)
∂ ln L ∂ ln L
) , а коэффициенты ci = ci (θ ) удовлетворяют системе
∂θi ∂θi
r
∑a c
j =1
ij
j
=
∂τ
, i = 1, , r .
∂θi
Если матрица A = {aij } обратима и A−1 = {aij } , то Dθ t ≥ ∑ a ij
∂τ ∂τ
.
∂θi ∂θ j
При этом знак равенства достигается тогда и только тогда, когда оценка имеет вид
t ( x) − τ (θ ) =
∑ ci (θ )
∂ ln L
,
∂θi
где ci (θ ) − функции, зависящие лишь от θ .
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
26
3. Методы нахождения оценок
3.1. Оценки максимального правдоподобия
Предположим, что СВ X 1 ,..., X n образуют случайную выборку. Обозначим через
P( x | θ ) распределение вероятностей или плотностью распределения СВ X i . Здесь θ ─
скалярный или векторный параметр θ ∈ Ω . Совместное распределение случайных величин
обозначим через Ln ( x | θ ).
Предположим, что случайный вектор x = ( x1 ,...xn ) имеет дискретное распределение.
Если вероятность Ln ( x | θ ) получить наблюдаемое значение x велика при θ = θ 0 и мала при
остальных значениях θ , то естественно в качестве оценки θ взять θ 0 . Эта концепция
формализуется в следующем определении для каждого возможного вектора наблюдений x,
пусть θˆ θˆ( x1 ,...xn ) ∈ Ω обозначаем значение θ , для которого функция Ln ( x | θ ) принимает
=
максимальное значение, т.е.
L( x | θˆ) ≥ L( x | θ )
для всех
θ ∈ Ω , или, что то же
самое, L( x | θˆ) = max L( x | θ ) .
Такая оценка θˆ параметра θ называется оценкой максимального правдоподобия
(сокращенно о.м.п.).
Будем предполагать, что Ω ─ подмножество Евклидова пространства, и для каждого
x = ( x1 ,...xn ) максимум функции правдоподобия Ln ( x | θ ) достигается во внутренней точке
множества Ω . Отсюда следует, в частности, что о.м.п. θˆ удовлетворяет условию
∂
∂
∂
∂L
∂ ln L
L=(
L,...,
L) ,
= 0 или
= 0 при θ = θˆ ,
∂θ
∂θ1
∂θ3
∂θ
∂θ
когда θ ─ векторный параметр.
Замечание 1. Эффективная оценка для числового параметра θ может быть получена
методом максимального правдоподобия, так как
∂ ln L
= A(θ )(t ( x) − θ ) ,
∂θ
откуда следует, что решение (ln L)′ = 0 имеет вид θˆ = t ( x) .
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
27
Замечание 2. О.м.п. есть функция от достаточной статистики. Действительно, если
существует достаточная статистика для параметра θ , то
Ln ( x | θ ) = g (T ( x) | θ ) h( x),
(3.1)
отсюда
∂ ln Ln ( x | θ ) ∂
=
ln g (T ( x) | θ ) .
∂θ
∂θ
Пусть при θˆ функция правдоподобия Ln ( x | θ ) принимает максимальное значение.
Из (3.1) следует, что при θˆ функция g (T ( x) | θ ) также принимает максимальное значение. Так
как g (T ( x) | θ ) зависит от x только через функцию T ( x) , то и θˆ будет функцией от T ( x) .
Пример 1. Пусть x1 , , xn имеют распределение N ( µ , σ 2 ) в данном случае
=
Ln ( x | θ )
n
1
1
1
1
2
exp{− 2 ( x=
exp{− 2
∏
k − µ) }
n
n /2
2σ
2σ
σ (2π )
1 σ 2π
n
∑ (x
k
− µ )2 } .
1
Предположим, что параметры µ и σ 2 неизвестны.
Найдем о.м.п. θˆ = ( µˆ , σˆ 2 ) . Имеем
1
n
n
ln L =
− ln 2π − ln σ 2 −
2
2
2σ 2
∂
1
=
ln L
∂µ
σ2
n
∑ (x − µ) ,
2
i
i =1
n
− µ)
∑ (x =
k
0,
1
∂ ln L
n
1
=
− 2+ 4
2
∂σ
2σ
2σ
∑ (x
k
− µ )2 =
0,
откуда
µˆ= x=
1 n
1 n
2
ˆ
( xk − x) 2 .
xk , σ
=
∑
∑
n 1
n 1
Пример 2. Предположим, что СВ имеют равномерное распределение на интервале
(0, θ ) , причем значение параметра θ неизвестно
1
 , 0 ≤ x ≤θ,
p ( x | θ ) = θ
0, x ∉ [0, θ ],
1
1,..., n
 , xi ∈ [0, θ ], i =
L n ( x | θ ) = θ n
0,в остальных случаях.
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
(3.2)
28
Из (3.2) видно, что о.м.п. для θ является такое значение θ , при котором xi ≤ θ и при
котором функция 1/ θ n принимает максимальное значение. Так как 1/ θ n ─ убывающая
функция, то такой оценкой будет θˆ = max( x1 ,..., xn ) .
Пример 3. (когда не существует о.м.п.). Пусть
1
 ,0 < x <θ,
p ( x | θ ) = θ
0, x ∉ (0, θ ).
В этом примере значение θˆ = max( x1 ,..., xn ) не подходит, так как θ должно быть
строго больше каждого из xi , i = 1,..., n. Поскольку θ может выбрано как угодно близко к
max( x1 ,..., xn ) , но не может совпадать с ним, то из этого следует, что о.м.п. не существует.
Пример 4. (неединственность о.м.п.). Пусть СВ X 1 ,..., X n имеют равномерное
распределение на интервале ( θ , θ + 1 ), причем значение θ неизвестно ( −∞ < θ < ∞ )
1,для θ ≤ xi ≤ θ +1, i =1,..., n,
Ln ( x | θ ) = 
0,в остальных случаях.
(3.3)
Условие θ ≤ xi для i = 1,..., n эквивалентно условию θ ≤ min( x1 ,..., xn }. Аналогично,
xi ≤ θ + 1 , i = 1,..., n , эквивалентно условию θ ≥ max( xi ) − 1 , т.е. (3.2) имеет вид
1, max( x1 ,... xn ) − 1 ≤ θ ≤ min( x1 ,..., xn )
Ln ( x | θ ) = 
0,в остальных случаях.
Таким образом, любое значение θ из интервала [max( x1 ,...xn ) − 1, min( x1 ,..., xn )] ,
является о.м.п.
Свойство 1. Если параметры θ
и τ = g (θ )
связаны взаимно однозначной
зависимостью, то их о.м.п. связаны той же зависимостью. Пусть θ = h(τ ) обозначает
обратную к τ = g (θ ) функцию. Тогда выражая через новый параметр τ
максимального
правдоподобия τ
правдоподобия
получаем
Ln ( x | h(τ )).
будет такое значение τ , при котором
Оценкой
функцию
максимального
Ln ( x | h(τ ))
принимает
максимальное значение при θ = θˆ , то из этого следует, что Ln ( x | h(τ )) принимает
максимальное значение при h(τ ) = θ . Таким образом, о.м.п. τ должна удовлетворять
следующему уравнению h(τ ) = θˆ , что эквивалентно τ = g (θˆ) , что и требовалось доказать.
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
29
Пример 5. В примере 1 мы нашли о.м.п. µ̂ и σˆ 2 . Определим теперь о.м.п. для σ и
Mx 2 . Из свойства 1 сразу следует, что о.м.п. для σ будет корень квадратный из выборочной
2
дисперсии σˆ 2 . Далее, так как Mx=
σ 2 + µ 2 , то о.м.п. для Mx 2 будет σˆ 2 + µˆ 2 .
3.2. Состоятельность оценки максимального правдоподобия
Обозначим через Ω множество значений неизвестного параметра θ . Будем считать,
что множество X тех x , для которых p ( x | θ ) ≠ 0 , не зависит от θ . Так как нас не интересуют
те x , для которых p ( x | θ ) = 0 , то окончательно будем считать, что функция p ( x | θ )
определена на X × Ω .
Обозначим через θ 0 истинное значение параметра θ и через Ω0 ─ некоторую
окрестность θ 0 , Ω0 ∈ Ω . Можно показать, что при довольно общих предложениях о.м.п. θˆn :
1) состоятельна, т.е. при n → ∞ Pθ0 { θˆn − θ 0 > ε } → 0 для произвольного ε ;
1
2) асимптотически нормальна N (θ 0 , , B0−1 ) , т.е. распределение случайного вектора
n
n (θˆn − θ 0 ) сходится к многомерному нормальному распределению N (0, B0−1 ) , где
=
B0 B=
θ )}, bij (θ ) Mθ (
(θ 0 ), B(θ ) {bij (=
∂
∂
ln p
ln p );
∂θi
∂θ j
3) асимптотически эффективна, т.е. при n → ∞ effθ (θ n ) → 1 для всех θ , где по
определению эффективность н.о. t есть
effθ (t ) =
1
Dθ t −1Mθ (
∂ ln L 2
)
∂θ
.
Отметим, что всегда 0 ≤ effθ (t ) ≤ 1 , и эффективность оценки t равна единице для всех
θ , тогда и только тогда, когда сама оценка t является эффективной.
3.3. Метод моментов
Если распределение генеральной совокупности зависит от r неизвестных параметров
θ1 ,...,θ r и существует первые r моментов распределения
=
ak a=
1, , r ,
k (θ1 ,..., θ r ), k
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
30
то приравняв выборочные моменты α k∗ к теоретическим и решая систему уравнений
α k = α k (θ1 ,...,θ r ) ( k = 1, , r ), относительно θ i , найдем оценки θˆi неизвестных параметров.
Они будут являться функциями выборочных моментов.
P
P
→ ak (n → ∞) , то θˆi 
Поскольку α k ∗ 
→θi , т.е. оценки, полученные методом
моментов, состоятельны.
Пример 1. Пусть X 1 ,... X n ─ независимые случайные величины с плотностью
P( x)
распределения=
1
θ1
exp{−
( x − θ2 )
θ1
} , если x ≥ θ 2 и P( x) = 0 в противном случае.
Найдем оценки для неизвестных параметров θ1 , θ 2 . Для этого вычислим первые два
момента распределения:
α=
1
1
θ1
∞
∫ xe
θ
− ( x −θ 2 )/θ1
dx= θ1 + θ 2 ,
α2 =
θ 22 + 2θ1θ 2 + 2θ12 .
2
Приравнивая теоретические моменты выборочным и решая систему уравнений
∗
α1=
θˆ1 + θˆ2 ,
 ∗
2
2
α 2 =2θˆ1 + 2θˆ1θˆ2 + θˆ2 ,
находим
=
θˆ1
α 2∗ − (α1∗ ) 2 ,
θˆ2 =
α1∗ − α 2∗ − (α1∗ ) 2 .
3.4. Примеры решения задач
Задача №1.
Найти методом максимального правдоподобия по выборке x1 , x2 ...xn точную оценку
параметра для плотности распределения Вейбулла:
α
=
f ( x) αθ xα -1e-θ x , x=
> 0, α 2 ,
x1 = 2, x 2 = 5, x3 = 6, x 4 = 8, x5 = 10 .
Решение:
Запишем функцию правдоподобия:
L=
( x1 ,..., x5 , θ ) f ( x1 , θ ) f ( x2 , θ )=
⋅ ... ⋅ f ( xn , θ ) 2θ 2e −4θ 2θ 5e −25θ 2θ 6e −36θ 2θ 8e −64θ ×
25θ
=
×2θ 10e −100θ 4θ e −4θ 10θ e −=
12θ e −36θ 16θ e −64θ 20θ e −100θ 153600θ 5e −229θ .
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
31
Для удобства прологарифмируем функцию:
ln L( x1 ,..., x5 , θ ) = ln(153600θ 5e −229θ ) = ln153600 + 5ln θ − 229θ = 5ln θ − 229θ + 11.94 .
Для нахождения максимума функции правдоподобия найдем её производную по
параметру θ и найдем уравнение правдоподобия:
∂
ln L( x1 ,..., x5 , θ ) = 0 ,
∂θ
1
∂
(5ln θ − 229θ + 11.94) =5 − 229 =0 .
∂θ
θ
Отсюда
5
= 229 ⇒ θˆ=
θ
5
= 0.02 .
229
Задача №2.
Найти методом моментов по выборке 25.3, 23.1, 28.4, 26.9, 30.5, 22.8, 19.7 точечные
оценки параметров для плотности распределения:
λ λx
f ( x)
=
Γ(3 2)
e- λ x , x > 0.
Решение:
M=
M1 (λ=
)
1
+∞
∞
−∞
0
3
3
λ 2 x2
∫ xf ( x, λ )dx= ∫ Γ(3 2) e
+∞
−λ x
dx=
∞
3
t2
3 / 2 ⋅ Γ(3 2 + 1) 3
=
t λ x=
e − t dt=
=
;
∫
λ 0 Γ(3 2)
Γ(3 2) ⋅ λ
2λ
1
∞
∞
λ α xα +1 − λ x
1 t α +1 − t
M=
M 2 (λ , α =
) ∫ xf ( x, λ )dx= ∫
e dx= =
t λ x= 2 ∫
e dt=
2
λ 0 Γ(α )
Γ(α )
−∞
0
1 Γ(α + 2) α (α + 1) 15
;
= 2 = =
λ Γ(α )
λ2
4λ 2
D(λ , α ) = M 2 (λ , α ) − M12 (λ , α ) =
15
9
6
3
− 2 = 2 = 2.
2
4λ
4λ
4λ
2λ
Среднее выборочное значение:
x=
1 n
1
(19.7 + 22.8 + 23.1 + 25.3 + 26.9 + 28.4 + 30.5)= 25.2 .
xi ⇒ x=
∑
7
n i =1
Дисперсия:
2
S=
1 n
1
2
( xi − x ) 2 ⇒ S =
(5.52 + 2.42 + 2.12 + 0.12 + 1.7 2 + 3.22 + 5.32=
) 11.66 .
∑
7
n i =1
Тогда имеем
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
32
=
λˆ
=
λˆ
x
x2
ˆ
=
α
,
,
S2
S2
25.2
25.22
= 2.15;=
αˆ = 54.3 .
11.66
11.66
Задача №3.
СВ X принимает два значения 1 и 0 с вероятностями P{x = 1}= λ , P{x = 0}= 1 − λ .
Пусть в результате m испытаний исход x = 1 осуществился k раз, а исход x = 0
осуществился m − k раз. Требуется получить оценку вероятности λ по результатам опыта.
Решение:
В
данном
примере
функция
правдоподобия
определяется
биномиальным
распределением L=
(λ ) λ k (1 − λ ) m −k . Уравнение правдоподобия принимает вид
k m−k
∂
ln L(λˆ ) =−
0.
=
∂λˆ
λˆ 1 − λˆ
k
Отсюда получаем решение λˆ = . Следовательно, оценкой вероятности P{x= 1}= λ
m
является относительная частота
k
исхода x = 1 .
m
Задача №4.
Некоторая нормально распределенная СВ
λ
измеряется независимо двумя
неравноточными приборами, которые осуществляют измерения без систематических ошибок,
но с разными дисперсиями D1 и D 2 . Нужно указать результирующую погрешность измерения
СВ λ .
Решение:
Обозначим показания первого и второго приборов соответственно через η1 и η2 .
Можем записать η1= λ + ξ1 , η2= λ + ξ 2 , где ξ1 , ξ2 - независимые нормально распределенные
СВ с нулевыми математическими ожиданиями и дисперсиями D1 , D 2 .
Нетрудно убедиться, что функция правдоподобия СВ λ определяется выражением
L ( λ=
) p (η1 ,η 2 | λ=
)
 (η − λ ) 2 (η 2 − λ ) 2 
−
exp  − 1
.
2πσ 1σ 2
2D1
2D 2 

1
Уравнение правдоподобия принимает вид
(η − λˆ ) (η 2 − λˆ )
∂
+
= 0.
ln L(λˆ ) = 1
D1
D2
∂λˆ
Отсюда находим
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
33
=
λˆ
D2
D1
η1 +
η2 .
D1 + D 2
D1 + D 2
Дисперсия такой оценки равна
Dλˆ =
D1D 2
.
D1 + D 2
Задача №5.
Под наблюдение поставлено N = 8 изделий. Наблюдения ведутся до отказа всех
изделий, при появлении отказа отказавшее изделие не заменяется новым. Наработки до отказа
в часах каждого из них приведены ниже.
N
N
xi
xi
1 100 5
520
2 170 6
680
3 250 7
1200
4 400 8
1500
Известно, что наработки подчинены экспоненциальному закону:
=
f ( x) λ e − λ x , x ≥ 0.
Для данных условий нужно определить точечную оценку λ̂ параметра λ .
Решение:
Для данного типа наблюдений справедлива формула
λˆ =
N −1
N
∑x
i =1
.
i
Подставляя в это выражение указанные значения, получаем:
λˆ
8 −1
= 0.00166 (1/÷).
100 + 170 + 250 + 400 + 520 + 680 + 1200 + 1500
Задача №6.
Под наблюдение поставлено N = 20 приборов. За время испытания ( T = 2000 ч)
отказало восемь приборов, время наработки до отказа каждого из них, равные xi , приведены в
предыдущей задаче. Известно, что наработки подчинены экспоненциальному закону.
Необходимо определить оценку λ̂ параметра λ .
Решение:
Для данного типа наблюдений справедлива формула
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
34
λˆ =
d
d
∑ x + ( N − d )T
i =1
,
i
где d - количество отказавших приборов. Из задачи 5 имеем
d
∑x
i =1
i
= 4820 . Подставляя
заданные величины в формулу для λ̂ , находим:
=
λˆ
8
8
= = 0.00028 (1/÷).
4820 + (20 − 8) ⋅ 2000 28820
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
35
ПРИЛОЖЕНИЕ 1
=
Таблица значений функции
ϕ ( õ)
 x2 
1
exp  − 
2π
 2
6
7
3982 3980
3939 3932
3857 3847
3739 3726
3589 3572
3410 3391
3209 3187
2989 2966
2756 2732
2516 2492
2275 2251
2036 2012
1804 1781
1582 1561
1374 1354
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
0
0,3989
3970
3910
3814
3683
3521
3332
3123
2897
2661
0,2420
2179
1942
1714
1497
1
3989
3965
3902
3802
3668
3503
3312
3101
2874
2637
2396
2155
1919
1691
1476
2
3989
3961
3894
3790
3652
3485
3292
3079
2850
2613
2371
2131
1895
1669
1456
3
3988
3956
3885
3778
3637
3467
3271
3056
2827
2589
2347
2107
1872
1647
1435
4
3986
3951
3876
3765
3621
3448
3251
3034
2803
2565
2323
2083
1849
1626
1415
5
3984
3945
3867
3752
3605
3429
3230
ЗОН
2780
2541
2299
2059
1826
1604
1394
1,5
1295
1276
1257
1238
3219
1200
1182
1,6
1109
1092
1074
1057
1040
1023
1,7
0940
0925
0909
0893
0878
1,8
0790
0775
0761
0748
1,9
0656
0644
0632
0,0540 0529
2,0
8
3977
3925
3836
3712
3555
3372
3166
2943
2709
2468
2227
1989
1758
1539
1334
9
3973
3918
3825
3697
3538
3352
3144
2920
2685
2444
2203
1965
1736
1518
1315
1163
1145
1127
006
0989
0973
0957
0863
0848
0833
0818
0804
0734
0721
0707
0694
0681
0669
0620
0608
0596
0584
0573
0562
0551
0519
0508
0498
0488
0478
0468
0459
0449
2,1
0440
0431
0422
0413
0404
0396
0387
0379
0371
0363
2,2
0355
0347
0339
0332
0325
0317
0310
0303
0297
0290
2,3
0283
0277
0270
0264
0258
0252
0246
0241
0235
0229
2,4
0224
0219
0213
0208
0203
0198
0194
0189
0184
0180
2,5
0175
0171
0167
0163
0158
0154
0151
0147
0143
0139
2,6
0136
0132
0129
0126
0122
0119
0116
0113
0110
0107
2,7
0104
0101
0099
0096
0093
0091
0088
0086
0084
0081
2,8
0079
0077
0075
0073
0071
0069
0067
0065
0063
0061
2,9
0060
0058
0056
0055
0053
0051
0050
0048
0047
0043
3,0
0,004
0043
0042
0040
0039
0038
0037
0036
0035
0034
3,1
0033
0032
0031
0030
0029
0028
0027
0026
0025
0025
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
36
Продолжение таблицы значений функции
=
ϕ ( õ)
 x2 
1
exp  − 
2π
 2
3,2
0024
0023
0022
0022
0021
0020
0020
0019
0018
0018
3,3
0017
0017
0016
0016
0015
0015
0014
0014
0013
0013
3,4
0012
0012
0012
0011
0011
0010
0010
0010
0009
0009
3,5
0009
0008
0008
0008
0008
0007
0007
0007
0007
0006
3,6
0006
0006
0006
0005
0005
0005
0005
0005
0005
0004
3,7
0004
0004
0004
0004
0004
0004
0003
0003
0003
0003
3,8
0003
0003
0003
0003
0003
0002
0002
0002
0002
0002
3,9
0002
0002
0002
0002
0002
0002
0002
0002
0001
0001
Оглавление
Сидняев Н.И., Мельникова Ю.С. «Оценки статистических параметров распределений»
ПРИЛОЖЕНИЕ 2
Критические точки распределения χ 2 Пирсона
Число
степеней
свободы k
0.01
0.025
0.05
0.95
0.975
0.99
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
6.6
9.2
11.3
13.3
15.1
16.8
18.5
20.1
21.7
23.2
24.7
26.2
27.7
29.1
30.6
32.0
33.4
34.8
36.2
37.6
38.9
40.3
41.6
43.0
44.3
45.6
47.0
48.3
49.6
50.9
5.0
7.4
9.4
11.1
12.8
14.4
16.0
17.5
19.0
20.5
21.9
23.3
24.7
26.1
27.5
28.8
30.2
31.5
32.9
34.2
35.5
36.8
38.1
39.4
40.6
41.9
43.2
44.5
45.7
47.0
3.8
6.0
7.8
9.5
11.1
12.6
14.1
15.5
16.9
18.3
19.7
21.0
22.4
23.7
25.0
26.3
27.6
28.9
30.1
31.4
32.7
33.9
35.2
36.4
37.7
38.9
40.1
41.3
42.6
43.8
0.0039
0.103
0.352
0.711
1.15
1.64
2.17
2.73
3.33
3.94
4.57
5.23
5.89
6.57
7.26
7.96
8.67
9.39
10.1
10.9
11.6
12.3
13.1
13.8
14.6
15.4
16.2
16.9
17.7
18.5
0.00098
0.051
0.216
0.484
0.831
1.24
1.69
2.18
2.70
3.25
3.82
4.40
5.01
5.63
6.26
6.91
7.56
8.23
8.91
9.59
10.3
11.0
11.7
12.4
13.1
13.8
14.6
15.3
16.0
16.8
0.00016
0.020
0.115
0.297
0.554
0.872
1.24
1.65
2.09
2.56
3.05
3.57
4.11
4.66
5.23
5.81
6.41
7.01
7.63
8.26
8.90
9.54
10.2
10.9
11.5
12.2
12.9
13.6
14.3
15.0
Уровень значимости α
38
ПРИЛОЖЕНИЕ 3
Критические точки распределения Стьюдента tα,k
Число
Уровень значимости α (двусторонняя критическая область)
степеней
свободы
0.10
0.05
0.02
0.01
0.002
0.001
k
1
6.31
12.7
31 .82
63.7
318.3
637.0
2
2.92
4.30
6.97
9.92
22.33
31.6
3
2.35
З.18.
4.54
5.84
10.22
12.9
4
2.13
2.78
3.75
4.60
7.17
8.61
5
2.01
2.57
3.37
4.03
5.89
6.86
6
1.94
2.45
3.14
3.71
5.21
5.96
7
1.89
2.36
3.00
3.50
4.79
5.40
8
1.86
2.31
2.90
3.36
4.50
5.04
9
1..83
2.26
2.82
3.25
4.30
4.78
10
1.81
2.23
2.76
3.17
4.14
4.59
11
1.80
2.20
2.72
3.11
4.03
4.44
12
1.78
2.18
2.68
3.05
3.93
4.32
13
1.77
2.16
2.65
3.01
3.85
4.22
14
1.76
2.14
2.62
2.98
3.79
4.14
15
1.75
2.13
2.60
2.95
3.73
4.07
16
1.75
2.12
2.58
2.92
3.69
4.01
17
1.74
2.11
2.57
2.90
3.65
3.96
18
1.73
2.10
2.55
2.88
3.61
3.92
19
1.73
2.09
2.54
2.86
3.58
3.88
20
1.73
2.09
2.53
2.85
3.55
3.85
21
1.72
2.08
2.52
2.83
3.53
3.82
22
1.72
2.07
2.51
2.82
3.51
3.79.
23
1.71
2.07
2.50
2.81
3.49
3.77
24
1.71
2.06
2.49
2.80
3.47
3.74
25
1.71
2.06
2.49
2.79
3.45
3.72
26
1.71
2.06
2.48
2.78
3.44
3.71
27
1.71
2.05
2.47
2.77
3.42
3.69
28
1.70
2.05
2.46
2.76
3.40
3.66
29
1.70
2.05
2.46
2.76
3.40
3.66
30
1.70
2.04
2.46
2.75
3.39
3.65
40
1.68
2.02
2.42
2.70
3.31
3.55
60
1.67
2.00
2.39
2.66
3.23
3.46
120
1.66
1.98
2.36
2.62
3.17
3.37
∞
1.64
1.96
2.33
2.58
3.09
3.29
0.05
0.025
0.01
0.005
0.001
0.0005
Уровень значимости α
(односторонняя критическая область)
39
ПРИЛОЖЕНИЕ 4
1
Значения функции Лапласа Ô ( z ) =
2π
z
∫e
−
t2
2
dz
−∞
Z
Ф(z)
Z
Ф(z)
Z
Ф(z)
Z
Ф(z)
0.0
0.5000
1.6
0.9452
-3
0.0013
-1.4
0.0803
0.1
0.5398
1.7
0.9554
-2.9
0.0019
-1.3
0.0968
0.2
0.5793
1.8
0.9641
-2.8
0.0026
-1.2
0.1151
0.3
0.6179
1.9
0.9713
-2.7
0.0035
-1.1
0.1357
0.4
0.6554
2.0
0.9772
-2.6
0.0047
-1.0
0.1587
0.5
0.6915
2.1
0.9821
-2.5
0.0062
-0.9
0.1841
0.6
0.7257
2.2
0.9861
-2.4
0.0082
-0.8
0.2119
0.7
0.7580
2.3
0.9893
-2.3
0.0107
-0.7
0.2420
0.8
0.7881
2.4
0.9918
-2.2
0.0139
-0.6
0.2743
0.9
0.8159
2.5
0.9838
-2.1
0.0179
-0.5
0.3085
1.0
0.8413
2.6
0.9953
-2.0
0.0228
-0.4
0.3446
1.1
0.8643
2.7
0.9965
-1.9
0.0287
-0.3
0.3821
1.2
0.8849
2.8
0.9974
-1.8
0.0359
-0.2
0.4207
1.3
0.9032
2.9
0.9981
-1.7
0.0446
-0.1
0.4602
1.4
0.9192
3.0
0.9987
-1.6
0.0548
-0.0
0.5000
1.5
0.9332
-
-1.5
0.0668
40
Список литературы
1.
Сидняев
Н.И.
Теория
вероятностей
и
математическая
статистика:
учебник/Н.И.Сидняев. – М.: Издательство Юрайт; ИД Юрайт, 2011. – 219 с.
2. Сборник задач по математике для втузов. Ч.3. Теория вероятностей и
математическая статистика/Под ред. А.В.Ефимова – М.: Наука, 1990. – 428 с.
3. Руководство для инженеров по решению задач теории вероятностей/Под ред.
А.А.Свешникова – Ленинград: Судпромгиз, 1962. – 423 с.
4. Гурский Е.И. Сборник задач по теории вероятностей и математической
статистике/Е.И.Гурский – Минск: Высшая школа, 1975. – 250 с.
5. Сборник задач по теории вероятностей, математической статистике и теории
случайных функций/Под ред. А.А.Свешникова – М.: Наука, 1970. – 656 с.
6. Закс Л. Статистическое оценивание/Л.Закс – М.: Статистика, 1976. – 598 с.