Константинов Александр Алексеевич.
Группа: ОЭМИб-М10-20-1.
27.02.2022.
Практическое задание №1.
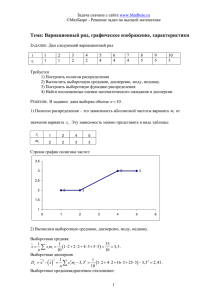
1. Построить полигон частот по заданному распределению выборки. Найти выборочное
среднее, выборочную дисперсию и СКО.
𝑥𝑖
𝑚𝑖
1
20
4
10
5
14
7
6
Расчетная таблица
x
1
4
5
7
Итого
Частота
𝑚𝑖
20
10
14
6
50
(𝑥 − 𝑥̅ )2 ∙ 𝑚𝑖
119,07
3,14
34,07
76,04
232,32
𝑥𝑚𝑖
20
40
70
42
172
В дискретном ряду выборочная средняя рассчитывается по формуле:
∑ 𝑥𝑖 𝑚𝑖
𝑥̅ =
∑ 𝑚𝑖
где 𝑥𝑖 – варианты значений признака; 𝑚𝑖 – частоты каждого из вариантов.
Для нашего задания:
∑ 𝑥𝑖 𝑚𝑖 172
𝑥̅ =
=
= 3,44
∑ 𝑚𝑖
50
Выборочная дисперсия для сгруппированных данных рассчитывается по формуле:
𝑆2 =
∑(𝑥𝑖 − 𝑥̅ )2 𝑚𝑖
∑ 𝑚𝑖
В нашем случае:
𝑆2 =
∑(𝑥𝑖 −𝑥̅ )2 𝑚𝑖
∑ 𝑚𝑖
=
232.32
50
≈ 4,65
Cреднеквадратическое отклонение S рассчитывается по формуле:
𝑆 = √𝑆 2 = √4,65 ≈ 2,16.
2. Построить полигон относительных частот по данному распределению выборки. Найти
выборочное среднее, выборочную дисперсию и СКО
𝑥𝑖
𝑚𝑖
𝑛
2
0,15
4
0,2
5
0,1
7
0,1
10
0,45
Расчетная таблица
x
2
4
5
7
10
Итого
𝑚𝑖
𝑛
0,15
0,20
0,10
0,10
0,45
1,00
𝑥
𝑚𝑖
𝑚𝑖
(𝑥 − 𝑥̅ )2 ∙
𝑛
𝑛
0,30
3,46
0,80
1,57
0,50
0,32
0,70
0,00
4,50
4,61
6,80
9,96
Выборочная средняя:
𝑥̅ =
Выборочная дисперсия 𝑆 2 =
∑ 𝑥𝑖 𝑚𝑖 6,8
=
= 6,8
∑ 𝑚𝑖
1,0
∑(𝑥𝑖 −𝑥̅ )2 𝑚𝑖
∑ 𝑚𝑖
=
9,96
1
= 9,96
Cреднеквадратическое отклонение S рассчитывается по формуле:
𝑆 = √𝑆 2 = √9,96 ≈ 3,16.
3. Из таблицы случайных чисел взяты 150 двузначных чисел (00 принимать за 100). Эти
числа были разбиты по десяткам на интервалы:
Δ𝑥𝑖
1-10
10-20
20-30
30-40
40-50
50-60
60-70
70-80
80-90
𝑚𝑖
16
15
19
13
14
19
14
11
13
90100
16
Построить гистограмму относительных частот и эмпирическую функцию распределения.
Найти выборочное среднее, выборочную дисперсию и СКО.
Расчетная таблица
𝑥𝑖
1
10
20
30
40
50
60
70
80
90
Итого
𝑥𝑖+1
10
20
30
40
50
60
70
80
90
100
Середин
а
интерва
ла
𝑥𝑖∗
5,50
15,00
25,00
35,00
45,00
55,00
65,00
75,00
85,00
95,00
Частот
а
𝑚𝑖∗
16
15
19
13
14
19
14
11
13
16
150
Накопле Относительн
нная
ая
частота
частота
𝑆𝑓
𝜔𝑖∗
0,11
16
0,10
31
0,13
50
0,09
63
0,09
77
0,13
96
0,09
110
0,07
121
0,09
134
0,11
150
1,00
Накопленна
я
относительн
ая
частота
𝜔𝑖нак
0,11
0,21
0,33
0,42
0,51
0,64
0,73
0,81
0,89
1,00
Плотность
относител
ь
ной
частоты
𝜔𝑖
ℎ𝑖
0,012
0,010
0,013
0,009
0,009
0,013
0,009
0,007
0,009
0,011
Относительная частота и плотность относительной частоты вычисляется по формулам
соответственно: 𝜔𝑖∗ =
𝜔𝑖нак
∑𝑖𝑖=1 𝜔𝑖∗ .
𝑛𝑖∗
𝑛
и
𝜔𝑖∗
ℎ
. Накопленные относительные частоты вычисляются по формуле:
=
Эмпирическая функция распределения находится по формуле:
𝑛𝑥
𝐹𝑛 (𝑥) =
𝑛
где
n – объем выборки,
𝑛𝑥 – количество наблюдений (вариантов) меньше x.
Когда результаты наблюдений представлены в виде интервального вариационного ряда,
то в качестве х принимают концы частичных интервалов, пользуясь данным выше
определением вычисляют значения эмпирической функции. Причем, при
𝑥 < 𝑥нач 𝐹(𝑥) = 0,
а при 𝑥 > 𝑥кон 𝐹(𝑥) = 1
Для задания получим таблицу:
x
F(x)
10
0,11
20
0,21
30
0,33
40
0,42
50
0,51
60
0,64
Эмпирическая функция распределения имеет вид:
70
0,73
80
0,81
90
0,89
100
1,00
0 при 𝑥 ≤ 1
0,11 при x = 10;
0,21 при x = 20;
0,33 при x = 30;
0,42 при x = 40;
∗ (x)
𝐹
= 0,51 при x = 50;
0,64 при x = 60;
0,73 при x = 70;
0,81 при x = 80;
0,89 при x = 90;
{ 1 при 𝑥 ≥ 100
Так как таблица определяет функцию распределения непрерывной случайной величины
не полностью, то при построении графика доопределяем функцию, соединяя точки графика,
соответствующие концам интервалов, отрезками.
Таблица для расчета числовых характеристик
Частота
𝑥𝑖 − 𝑥𝑖+1
1
10
10
20
20
30
30
40
40
50
50
60
60
70
70
80
80
90
90
100
Итого
𝑚𝑖
16
15
19
13
14
19
14
11
13
16
150
Средина
интервала
𝑥′
5,5
15
25
35
45
55
65
75
85
95
𝑥 ′ 𝑚𝑖
Выборочная средняя определяется по формуле
88
225
475
455
630
1045
910
825
1105
1520
7278,0
(𝑥 − 𝑥̅ )2 𝑚𝑖
29611,53
16853,86
10510,62
2376,28
173,47
797,82
3802,27
7713,09
17300,28
34566,25
123705,44
∑ 𝑥𝑖′ 𝑚𝑖
𝑥̅ =
∑ 𝑚𝑖
где 𝑥𝑖′ – середины интервалов; 𝑚𝑖 – частоты интервалов.
Выборочная средняя:
𝑥̅ =
∑(𝑥𝑖′ −𝑥̅ )2 ∙𝑚𝑖
Выборочная дисперсия: 𝑆 2 =
В нашем случае: 𝑆 2 =
123705,44
150
∑ 𝑥𝑖′ 𝑚𝑖 7278
=
= 48,52
∑ 𝑚𝑖
100
𝑛
≈ 824,7
4. В условии заданий не были найдены переменные m и n. Просьба в коментарии к этому
заданию ответить что делать в данной ситуации.
5. Измерение роста (в см) случайно отобранных 100 курсантов дали следующие
результаты:
Рост
Число
курсантов
158-162
2
162-166
2
166-170
36
170-174
25
174-178
15
178-182
12
182-186
8
Найти выборочную среднюю и выборочную дисперсию роста обследованных курсантов
Таблица для расчета числовых характеристик
Рост,
Частота
Средина
см.
интервала
𝑥𝑖 − 𝑥𝑖+1
𝑚𝑖
𝑥′
158
162
2
160
162
166
2
164
166
170
36
168
170
174
25
172
174
178
15
176
178
182
12
180
182
186
8
184
Итого
100
𝑥 ′ 𝑚𝑖
320
328
6048
4300
2640
2160
1472
17268,0
Выборочная средняя:
𝑥̅ =
Выборочная дисперсия: 𝑆 2 =
∑ 𝑥𝑖′ 𝑚𝑖
∑ 𝑚𝑖
3105б76
100
=
17268
100
≈ 31,06
= 172,68 см
(𝑥 − 𝑥̅ )2 𝑚𝑖
321,56
150,68
788,49
11,56
165,34
642,99
1025,14
3105,76