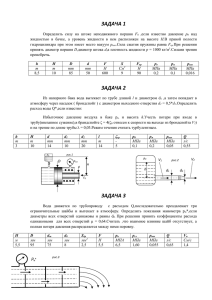
Задача №1 На рис.№1 представлено начальное положение гидравлической системы дистанционного управления (рабочая жидкость между поршнями не сжата). При перемещении ведущего поршня (его диаметр D) вправо жидкость постепенно сжимается и давление в ней повышается. Когда манометрическое давление рм достигает определённой величины, сила давления на ведомый поршень (его диаметр d) становится больше силы сопротивления F, приложенной к штоку ведомого поршня. С этого момента приходит в движение вправо и ведомый поршень. Диаметр соединительной части цилиндров δ, длина l. Требуется определить диаметр ведущего поршня D, необходимого для того, чтобы при заданной величине силы F ход L обоих поршней был один и тот же. Коэффициент объёмного сжатия рабочей жидкости принять βw= 0,0005 1/МПа. Дано: d, = 36 мм = 36·10-3 м. L, = 50 мм = 50·10-3 м. δ, = 16 мм = 16·10-3 м. l, = 2,2 м. F, = 23,7 кН = 23,7·103 Н. βw= 0,0005 1/МПа. L d δ D F l L Рис.1 1 Решение. Ведомый поршень начнёт движение вправо, когда сила давления на него жидкости станет равной силе трения F. рм d2 4 F Манометрическое давление рм, при котором начнётся движение ведомого поршня, будет ровняться: рм F 4 F 2 d d2 4 4 23,7 10 3 Рм 0,02 10 9 Н / м 2 3 2 3,14 (36 10 ) Для достижения этого давления первоначальный объём жидкости должен быть уменьшен на некоторую величину ΔW. При её сжатии на основании формулы коэффициента объёмного сжатия эта величина равна: ΔW=βw·W·Pм где, ΔW W – первоначальный объём жидкости, равный d2 4 L 2 4 l С другой стороны, при сжатии жидкости на величину ΔW ведущий поршень должен пройти некоторую величину ΔL: d2 W w W Pм L, 4 Откуда L w W Pм . d2 4 После начала движения обоих поршней объём жидкости, вытесняемой из левой полости в правую полость на основании этого условия, должно выполняться равенство: d2 d2 L L L 4 4 2 D2 L w W Pм 4 D2 4 D2 4 D2 4 d2 4 L D2 2 d2 L w L l Pм L 4 4 4 L D2 4 L w Pм L 1 w Pм d2 4 d2 4 L w L w 2 2 4 4 l Pм l Pм D 2 L 1 w Pм d 2 L w 2 l Pм Откуда искомая величина D будет равняться: D D d 2 L w 2 l Pм L 1 w Pм 36 10 3 2 2 50 10 3 0,0005 10 6 16 10 3 2,2 0,02 109 0,0396 м 50 10 3 1 0,0005 10 6 0,02 109 Требуемый диаметр поршня D = 0,0396 метра. 3 Задача №2 Вал диаметром D вращается во втулке длиной l с частотой n. При этом зазор между валом и втулкой толщиной δ заполнен маслом, имеющим плотность ρ и кинематическую вязкость υ (рис.2). Требуется определить величину вращающего момента М, обеспечивающего заданную частоту вращения. Дано: D = 200 мм = 0,2 м. l = 450 мм = 0,45 м δ = 1,5 мм = 0,0015 м ρ = 960 кг/м3 v = 0,15 см2/с = 0,15·10 -6 м2/с n = 100 1/мин. ≈ 1,67 1/с D δ l M Рис.2 4 Решение. При решении задачи применяем формулу Ньютона для силы F. F dV S dh Где, μ – динамический коэффициент вязкости жидкости, µ=ν·ρ, µ=0,15∙10-6∙960=0,000144 dV - градиент скорости. Поскольку толщина слоя масла, можно считать, dh что, скорости изменяются в нём по прямолинейному закону, при этом градиент dV V будет равняться , где V – скорость на поверхности вала, dh равна линейной скорости вращения: V D l 60 3,14 0,2 0,45 0,00471м 2 / с 60 dV V 0,00471 3,14 dh 0,0015 S – площадь соприкосновения слоёв, м2 S=π∙D∙l=3,14∙0,2∙0,45=0,2826 м2 Находим силу F по формуле Ньютона: F dV S 0,000144 3,14 0,2826 0,0001278 Н. ≈1,28∙10 -4Н. dh Искомый вращающий момент М равняется: M F D 0,0001278 0,2 0,00001278 1,28 10 5 Н м 2 2 5 Задача №3. Определить показания мановакуумметра Р, если к штоку поршня приложена сила F, его диаметр d, высота жидкости Н, плотность ρ. (рис.3) d H Рмв F Рис.3 Дано: F=0,2 кН=0,2∙103Н d=150 мм = 0,15м Н=2 м ρ=850 кг/м3 Решение. Искомая величина давления р определяется из равенства силы давления на поршень со стороны жидкости и силы приложенной к штоку. d2 р g H F 4 Отсюда, p 4 F gH d2 4 0,2 10 3 p 850 9,8 2 5336,57 Н/м2 3,14 0,15 2 6 Задача №4 Гидравлический повыситель давления (мультипликатор) (рис.4) имеет поршень диаметром D и скалку диаметром d. Требуется определить, под каким начальным давлением р1 должна подаваться жидкость под большой поршень, чтобы давление на выходе из мультипликатора было р2. Трением в уплотнениях и весом поршня со скалкой пренебречь. Р2 d D Р1 Рис.4 Дано: D=150 мм = 0,15 м. d=50 мм = 0,05 м. Р2= 8 МПа = 8∙106 Па. 7 Решение. Задача решается на основе уравнения равновесия сил гидростатического давления, действующих снизу на большой поршень и сверху на торец скалки. р1 D2 p2 4 D2 4 d p1 p 2 D Откуда 2 2 0,05 р1 8 10 888888,89 Па 0,89МПа 0,15 6 8 Задача №5 Вертикальный цилиндрический резервуар высотой Н и диаметром D закрывается полусферической крышкой, сообщающейся с атмосферой через трубу внутренним диаметром d (рис.5). резервуар заполнен мазутом плотность которого ρ=900 кг/м3. Требуется определить: 1. Высоту поднятия мазута h в трубе при повышении температуры на toС. 2. Усилие, отрывающее крышку резервуара при подъёме мазута на высоту h за счёт его разогрева. Коэффициент температурного расширения мазута принять равным βt=0,00072 1/оС. H h d D Рис.5 9 Дано: D= 2,5м H=3м d=300мм =0,3м t=20оС Решение. Определяем первоначальный объём мазута до его разогрева W D2 D 3,14 2,5 2 H 3 4 4 2,5 3 3 18,81м 3 Коэффициент температурного расширения определяется по формуле: t W W t Откуда приращение объёма мазута при его нагревании ΔW=βt∙W∙Δt= 0,00072∙18,81∙20=0,2709 м3 Этому приращению объёма будет соответствовать высота подъёма мазута в трубе равная h 4 W d2 h 4 0,2709 3,84 м 3,14 0,3 2 Усилие, открывающее крышку резервуара при подъёме мазута на высоту h равна весу мазута в объёме тела давления. Wпод Wпод D2 D 4 2 d2 D2 D d h D3 h h h 4 4 4 2 6 2 3,14 2,5 2 2,5 3,14 0,3 3,84 3,84 2,044 м 3 4 4 6 Искомая величина Ру=ρ∙g∙Wпод=900∙9,8∙2,044=18028,08 кг∙м/с2 10 Задача №6 Поршень диаметром D имеет n отверстий диаметром d каждое (рис.6). отверстия рассматривать как внешние цилиндрические насадки с коэффициентом расхода µ=0,82; плотность жидкости ρ=900 кг/м3. Определить скорость V перемещения поршня вниз, если к его штоку приложена сила F. Дано: D=55 мм =0,055м do=5 мм =0,005м ρ= 900 кг/м3 n= 3 F= 15 кН = 15000 Н µ= 0,82 F n- do n- do D Рис.6 11 Решение. Определим давление под поршнем Р F D 2 4 0 d 02 4 n d 2 o 4 F 4 15000 6367061,07 Па 2 D n do 3,14 0,055 2 3 0,005 2 2 4 3,14 0,005 2 0,0000196 м 2 4 Определим расход из отверстий под действием давления Q0 0 2 g Н 0 Q0 0,82 0,0000196 2 Р 2 6367061,07 0,00191м 3 / с 900 Суммарный расход из всех отверстий Q=n·Q0=3∙0,00191=0,00573 м3/с Скорость перемещения поршня V V Q 4Q 4 0,00573 2,41м / с 2 2 D D 3,14 0,055 2 4 12 Литература. 1. Гидравлика, гидромашины и гидроприводы./Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др.: Машиностроение, 1982. 2. Задачник по гидравлике, гидромашинам и гидроприводам. Учебное пособие для вузов / под ред. Б.Б.Некрасова. М.: Высшая школа, 1989. 3. Рабочая программа и задание на контрольные работы №1,2 с методическими указаниями для студентов III курса специальности. В.Т.СМ. РГОТУПС, Москва, 2002. 13