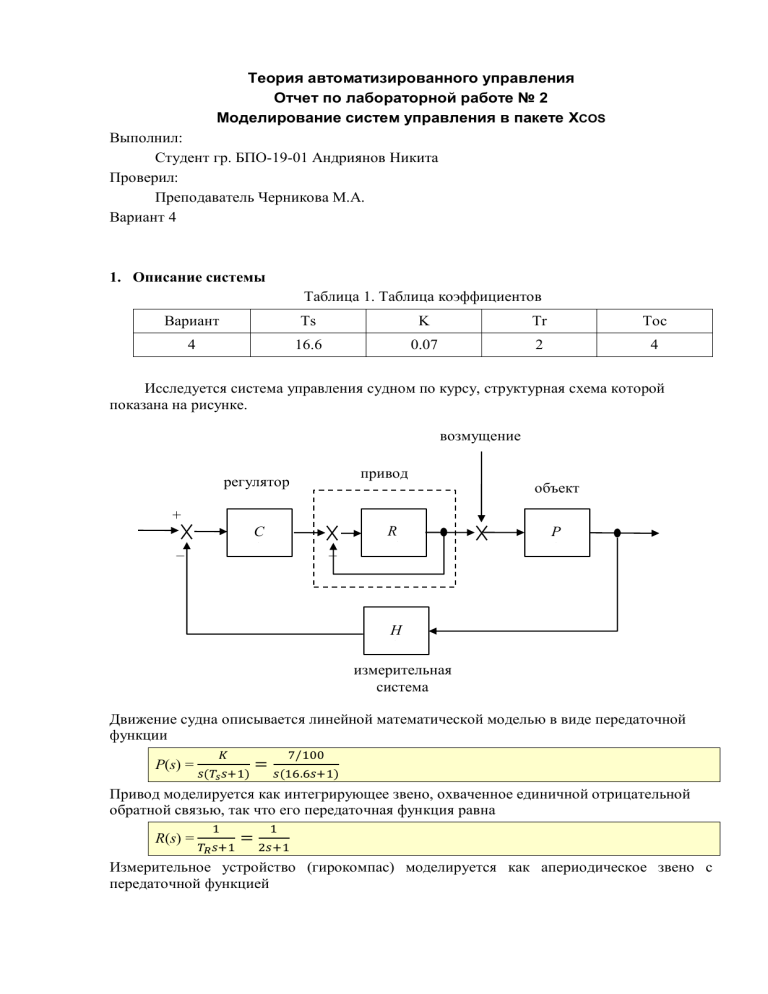
Теория автоматизированного управления Отчет по лабораторной работе № 2 Моделирование систем управления в пакете XCOS Выполнил: Студент гр. БПО-19-01 Андриянов Никита Проверил: Преподаватель Черникова М.А. Вариант 4 1. Описание системы Таблица 1. Таблица коэффициентов Вариант Ts K Tr Toc 4 16.6 0.07 2 4 Исследуется система управления судном по курсу, структурная схема которой показана на рисунке. возмущение привод регулятор объект + C (s – – R 0( P (s H (s измерительная система Движение судна описывается линейной математической моделью в виде передаточной функции P(s) = 𝐾 𝑠(𝑇𝑠 𝑠+1) = 7/100 𝑠(16.6𝑠+1) Привод моделируется как интегрирующее звено, охваченное единичной отрицательной обратной связью, так что его передаточная функция равна R(s) = 1 𝑇𝑅 𝑠+1 = 1 2𝑠+1 Измерительное устройство (гирокомпас) моделируется как апериодическое звено с передаточной функцией 1 H(s) = 𝑇𝑜𝑐 𝑠+1 = 1 4𝑠+1 2. Исследование системы с ПД-регулятором ● передаточная функция ПД-регулятора 13.53𝑠+0.7 C0(s) = 𝑠+1 ● модель Xcos системы с ПД-регулятором: ● переходные процессы в системе с ПД-регулятором при изменении курса на 10 градусов ● модель системы с ПД-регулятором с учетом внешнего возмущения ● переходные процессы в системе с ПД-регулятором при изменении курса на 10 градусов при действии возмущения ● передаточная функция по возмущению для системы с ПД-регулятором Wf0 = 0.0005271 +0.0036898s +0.0073795s² +0.0042169s³ -------------------------------------------------------------0.000369 +0.0146619s +0.1777108s² +0.9804217s³ +1.810241s⁴ +s⁵ судно с ПД-регулятором не вышло на заданный курс 10 градусов, потому что перадаточная функция в точке s=0 не содержит нуль, постоянные возмущения в установившемся режиме не компенсируются ● статический коэффициент усиления kf0= 1.4285714 ● установившееся значение сигнала выхода должно быть равно 𝜑∞ = 12.857143 потому что регулятор не содержит интегральный канал и в системе есть статическая ошибка при постоянном возмущении эти данные согласуются с результатами моделирования. 3. Исследование системы с ПИД-регулятором ● передаточная функция ПИД-регулятора 1 1 C(s) = = 𝑇𝑖 𝑠 200𝑠 ● модель системы с ПИД-регулятором с учетом внешнего возмущения ● передаточная функция по возмущению для системы с ПИД-регулятором Wf (s) = 0.0005271𝑠 +0.0036898𝑠² +0.0073795𝑠³ +0.0042169𝑠⁴ 0.0000026 +0.0003716𝑠 +0.0146619𝑠² +0.1777108𝑠³ +0.9804217𝑠⁴ +1.810241𝑠⁵ +𝑠⁶ при использовании ПИД-регулятора судно выходит на заданный курс, потому что перадаточная функция в точке s=0 содержит нуль, что соответствует АЧХ=0 на нулевой частоте, тогда постоянные возмущения в установившемся режиме компенсируются полностью ● статический коэффициент усиления kf0=0 ● установившееся значение сигнала выхода должно быть равно 𝜑∞ = 10 потому что регулятор содержит интегральный канал, поэтому в системе нет статической ошибки при постоянном возмущении эти данные согласуются с результатами моделирования. ● переходные процессы в системах с ПД- и ПИД-регуляторами ● при использовании ПИД-регулятора вместо ПД-регулятора (что улучшилось?) в системе нет статической ошибки при постоянном возмущении, возмущения в установившемся режиме компенсируются полностью ● при этом сигнал управления (как изменился?) изменился на необходимый заданный курс 10 градусов ● в то же время (что ухудшилось?) сигнал управления проходит до скачка, после чего устанавливается ● передаточная функция разомкнутой системы с ПИД-регулятором Wopen(s) = 0.00035 +0.04935𝑠 +0.9471𝑠² 𝑠² +23.6𝑠³ +130.2𝑠⁴ +240.4𝑠⁵ +132.8𝑠⁶ ● запасы устойчивости: по амплитуде gm= 18.582509 по фазе φm= 70.138686 Запасы являются достаточными как по амплитуде, так и по фазе. При изменении на заданные интервалы устойчивость системы потеряется. Однако данных значений достаточно, чтобы сохранять устойчивость при заданных условиях. Вывод Студент научился осваивать методы моделирования линейных систем в пакете XCOS. Исследуемая система с судном, движущимся на 10 градусов, работает оптимально под внешним воздействием с ПИД-системой. Потому что если регулятор содержит интегральный канал, то в системе нет статической ошибки при постоянном возмущении.









