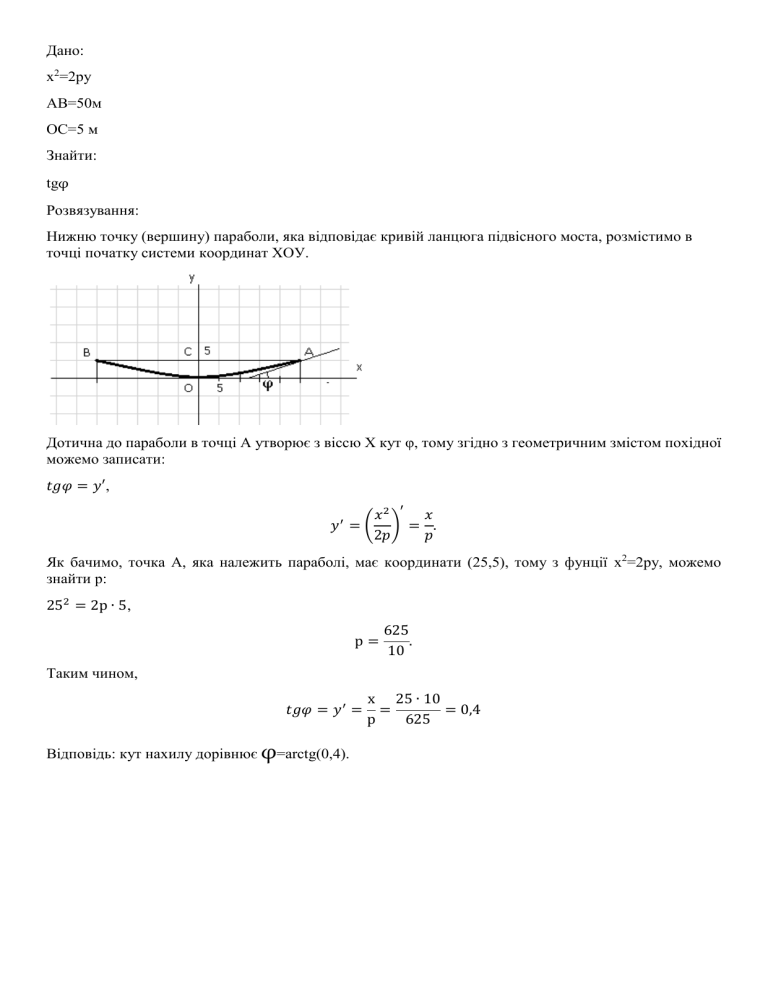
Дано: x2=2py АВ=50м ОС=5 м Знайти: tgφ Розвязування: Нижню точку (вершину) параболи, яка відповідає кривій ланцюга підвісного моста, розмістимо в точці початку системи координат ХОУ. Дотична до параболи в точці А утворює з віссю Х кут φ, тому згідно з геометричним змістом похідної можемо записати: 𝑡𝑔𝜑 = 𝑦′, ′ 𝑥2 𝑥 𝑦 =( ) = . 2𝑝 𝑝 ′ Як бачимо, точка А, яка належить параболі, має координати (25,5), тому з фунції x2=2py, можемо знайти р: 252 = 2р ∙ 5, р= 625 . 10 Таким чином, 𝑡𝑔𝜑 = 𝑦 ′ = Відповідь: кут нахилу дорівнює φ=arctg(0,4). х 25 ∙ 10 = = 0,4 р 625 Дано: 𝐼= 𝑘𝑠𝑖𝑛𝜑 . 𝑟2 R – радіус стола, r – відстань від світильника до краю стола, h – висота розміщення світильника над поверхнею стола, φ – кут нахилу проміня світла. Знайти: h для Imax Розв’язання: З малюнку бачимо, що 𝑠𝑖𝑛𝜑 = ℎ ℎ = . 𝑟 √ℎ2 + 𝑅 2 Тому 𝐼= 𝑘𝑠𝑖𝑛𝜑 𝑘ℎ 𝑘ℎ = = 2 𝑟 (ℎ2 + 𝑅 2 )√(ℎ2 + 𝑅 2 ) √(ℎ2 + 𝑅 2 )3 Щоб знайти наявність ектремумів, визначимо першу похідну І’(h): ′ I (h) = 3 k (√(h2 + R2 )3 − 2 ∙ √(h2 + R2 ) ∙ 2h ∙ h) 2 (√(h2 + R2 )3 ) k√(h2 + R2 )(h2 + R2 − 3h2 ) = = (h2 + R2 )3 k√(h2 + R2 )(R2 − 2h2 ) = . (h2 + R2 )3 Умовою наявності екстремуму є I′ = 0, це можливо лише при умові, що R2 − 2h2 = 0, R2 = 2h2 h= R √2 Дослідимо інтервали (0; R I′ ( ) = 2 I ′ (R) R √2 )і( R √2 ; +∞): R2 R2 k√( 4 + R2 ) (R2 − 2 ∙ 4 ) 3 R2 (4 + R2 ) R2 k 2 = > 0 − зростання функції 5 5 √( R2 ) 4 k√(R2 + R2 )(R2 − 2R2 ) k(−R2 ) = = < 0 − спадання функції. (R2 + R2 )3 √(2R2 )5 Робимо висновок, що при h = R √2 функція I′ (h) досягає свого мксимального значення. R Відповідь: максимум освітлення на краю стола буде при висоті h = світильника над поверхнею √2 стола . Це для розуміння – переписувать не треба)))) Для довідки: Троянда – плоска крива, її креслення схожий з малюнком квітки. Ця крива в полярній системі координат характеризується виразом: p = a sin k φ, де a і k – константи, що обумовлюють розмір (a) і чисельність пелюсток (k) обраної троянди. Вся лінія розміщена всередині окружності з радіусом а і при k > 1состоит з ідентичних за формою і розміром пелюсток. Чисельність пелюсток характеризується величиною k. При цілому k чисельність пелюсток буде k, коли k непарне і 2 k,- коли парне. Тобто, для нашого рівняння вже точно буде 8 пелюсток. 6.6 Побудувати графік функції, що задана в полярних координатах 𝜌 = 3 + 5𝑠𝑖𝑛4𝜑 рішення: 1) знайдемо ОВФ a) ρ≥0, тобто 3 + 5𝑠𝑖𝑛4𝜑 ≥ 0 5𝑠𝑖𝑛4𝜑 ≥ −3 3 5 3 4𝜑 ≥ (−1)𝑘 arcsin (− ) ± 2𝜋𝑘, 𝑘𝜖𝑍 5 𝑠𝑖𝑛4𝜑 ≥ − 1 3 𝜑≥ (−1)𝑘 3 𝜋 arcsin (− ) ± 𝑘, 𝑘𝜖𝑍 4 5 2 𝜑≥ (−1)𝑘 3 𝜋 arcsin (− ) ± 𝑘, 𝑘𝜖𝑍 4 5 2 𝜋 arcsin (− 5) ≈ − 20 або -9° 4 𝑏) − 1 ≤ 𝑠𝑖𝑛4𝜑 ≤ +1 𝜋 𝜋 − ± 2𝜋𝑘 ≤ 4𝜑 ≤ + ± 2𝜋𝑘, 𝑘 𝜖𝑍 2 2 𝜋 𝜋 𝜋 𝜋 − ± 𝑘 ≤ 𝜑 ≤ + ± 𝑘, 𝑘 𝜖𝑍 8 2 8 2 2) 𝜌 = 3 + 5𝑠𝑖𝑛4𝜑 є періодичною функцію Т=2π 𝜌(−𝜑) = 3 + 5sin 4(−𝜑) = 3 − 5𝑠𝑖𝑛4𝜑 – функція не є ні парною, ні непарною. 3) Побудуємо графік функції ρ=3+5sin4φ в декартовій системі координат Знайдемо точки перетину графіка з осями координат - ρ=0 3 + 5𝑠𝑖𝑛4𝜑 = 0 5𝑠𝑖𝑛4𝜑 = −3 3 5 3 4𝜑 = (−1)𝑘 arcsin (− ) + 2𝜋𝑘, 𝑘𝜖𝑍 5 𝑠𝑖𝑛4𝜑 = − 𝜑= (−1)𝑘 3 𝜋 arcsin (− ) + 𝑘, 𝑘𝜖𝑍 4 5 2 1 3 𝜋 𝜑1 = arcsin (− ) + 𝑘, 𝑘𝜖𝑍 4 5 2 1 3 𝜋 𝜋 𝜑2 = arcsin ( ) + + 𝑘, 𝑘𝜖𝑍 4 5 4 2 - 𝜑 = 0, ρ=3 𝜋 4) Дослідимо проміжки зростання та спадання на ділянці (0; 2 ) , а також знайдемо точки екстремума Перша похідна 𝜌′ = 20𝑐𝑜𝑠4𝜑 Умови існування −1 ≤ 𝑐𝑜𝑠4𝜑 ≤ +1 −𝜋 ± 2𝜋𝑘 ≤ 4𝜑 ≤ 0 ± 2𝜋𝑘, 𝑘 𝜖𝑍 𝜋 𝜋 𝜋 − ± 𝑘 ≤ 𝜑 ≤ 0 ± 𝑘, 𝑘 𝜖𝑍 4 2 2 Умова наявності екстремуму 𝜌′ = 0 20𝑐𝑜𝑠4𝜑 = 0 𝑐𝑜𝑠4𝜑 = 0 𝜋 4𝜑 = ± + 2𝜋𝑘, 𝑘 𝜖𝑍 2 𝜋 𝜋 𝜑 = ± + 𝑘, 𝑘 𝜖𝑍 8 4 𝜌′ (0) = 20𝑐𝑜𝑠0 = 20 > 0 𝜋 𝜋 𝜌′ ( ) = 20𝑐𝑜𝑠4 ( ) = −20 < 0 4 4 𝜋 𝜋 𝜌′ ( ) = 20𝑐𝑜𝑠4 ( ) = 20 > 0 2 2 𝜋 𝜋 𝜌 (− 20) = 3 + 5𝑠𝑖𝑛4 (− 4 ) =3 𝜋 𝜋 𝜌 ( 8 ) = 3 + 5𝑠𝑖𝑛4 ( 8 ) =8 𝜌(0) = 3 + 5𝑠𝑖𝑛0 =3 𝜋 𝜋 𝜌 ( 4 ) = 3 + 5sin(4 ∙ 4 ) =3 3𝜋 3𝜋 𝜌 ( ) = 3 + 5 sin (4 ∙ ) = −2 8 8 𝜋 інтервал [0; ] 8 Знак ρ’ + поведінка ρ ρ зростання 𝜋 8 0 max 𝜋 3𝜋 [ ; ] 8 8 - 3𝜋 8 0 min 8 спадання -2 [ 3𝜋 𝜋 ; ] 8 2 + зростання 5) Дослідимо проміжки опуклості та вигину і знайдемо точки перегину 𝑟′′ = 0 −80𝑠𝑖𝑛4𝜑 = 0 𝑠𝑖𝑛4𝜑 = 0 4𝜑 = 0 ± 𝜋𝑘, 𝑘 𝜖𝑍 𝜋 𝜑 = ± 𝑘, 𝑘 𝜖𝑍 4 А також −1 ≤ 𝑠𝑖𝑛4𝜑 ≤ +1 𝜋 𝜋 − + 2𝜋𝑘 ≤ 4𝜑 ≤ + 2𝜋𝑘, 𝑘 𝜖𝑍 2 2 𝜋 𝜋 𝜋 𝜋 − + 𝑘 ≤ 𝜑 ≤ + 𝑘, 𝑘 𝜖𝑍 8 2 8 2 інтервал 𝜋 [0; ] 4 𝜋 4 𝜋 𝜋 [ ; ] 4 2 Знак ρ’’ - 0 + перегин поведінка ρ ρ опукла 3 вогнута 6) Побудуємо графік функції Проведемо два кола, радіусами 2 (маленькі пелюстки) і 8 (великі пелюстки). Відкладемо критичні кути та на радіусах відкладемо відповідні точки для радіусів-векторів. Побудувавши пелюстки для кута кутів. 𝜋 8 3𝜋 і кута 8 , по аналогії накреслимо для інших критичних 6.4 Дослідити функцію 𝑥2 − 1 у= 2 𝑥 +1 та побудувати графік. Розв’язання: 1) ОВФ y(x) існує для будь-яких 𝑥 ∈ (−∞, +∞) Вертикальних асимптот і точок розриву немає. 2) Точки перетину графіка з осями координат: З віссю ОХ: у=0, 𝑥 2 − 1 = 0, 𝑥 2 = 1, 𝑥1 = −1, 𝑥2 = 1 З віссю ОY: x=0, 𝑦 = −1 Графік функції перетинає вісь ОХ в точках (-1,0) та (1,0) і вісь ОУ в точці (0,-1). 3) Періодичність та парність/непарність (𝑥+𝑇)2 −1 𝑥 2 +2𝑥𝑇+𝑇 2 −1 у(х+Т)= (𝑥+𝑇)2 +1 = 𝑥 2 +2𝑥𝑇+𝑇 2 +1 ≠ 𝑦(𝑥) + 𝑇 – неперіодична функція (−𝑥)2 −1 𝑥 2 −1 у(-х)= (−𝑥)2 +1 = 𝑥 2 +1 = 𝑦(𝑥) – парна функція, тому графік симетричний відносно осі ОУ. 4) Точок розриву немає, функція монотонна. 5) Інтервали монотонності, екстремуми у′ = (𝑥 2 − 1)′ ∙ (𝑥 2 + 1) − (𝑥 2 + 1)′ ∙ (𝑥 2 − 1) 2𝑥 ∙ (𝑥 2 + 1) − 2𝑥 ∙ (𝑥 2 − 1) = = (𝑥 2 + 1)2 (𝑥 2 + 1)2 2𝑥 ∙ (𝑥 2 + 1 − 𝑥 2 + 1) 4𝑥 = = 2 2 2 (𝑥 + 1) (𝑥 + 1)2 у′ = 0, якщо 4х=0, або х=0. Дослідимо знаки похідної зліва та справа від х=0. −4 = −1 < 0, ((−1)2 + 1)2 𝑦 ′ (−1) = 𝑦 ′ (1) = (12 4 =1>0 + 12 ) Інтервали монотонності матимуть вигляд: інтервали (−∞, 0) 0 (0, +∞) - 0 + Похідна Поведінка функції min, (-1) 6) Інтервали опуклості (4𝑥)′ ∙ (𝑥 2 + 1)2 − ((𝑥 2 + 1)2 )′ ∙ 4𝑥 4 ∙ (𝑥 2 + 1)2 − 16𝑥 2 ∙ (𝑥 2 + 1) у′ = = = (𝑥 2 + 1)4 (𝑥 2 + 1)4 ′ = (4𝑥 2 + 4 − 16𝑥 2 ) −12𝑥 2 + 4 = (𝑥 2 + 1)3 (𝑥 2 + 1)3 у′′ = 0, якщо −12𝑥 2 +4 (𝑥 2 +1)3 =0 −12𝑥 2 + 4 = 0 12𝑥 2 = 4 𝑥2 = 1 3 𝑥1 = − 1 , 𝑥2 = √3 1 . √3 Дослідимо знаки другої похідної на інтервалах (−∞, − (− ( 1 √3 1 , 1 ), 𝑦"(−1) = √3 1 ), 𝑦"(0) = √3 √3 , +∞), 𝑦"(1) = −12∙(−1)2 +4 ((−1)2 +1)3 −12∙(0)2 +4 ((0)2 +1)3 −12∙(1)2 +4 ((1)2 +1)3 = −8 8 = −1 < 0 4 =1=4>0 = −8 8 = −1 < 0 інтервали (−∞, − Друга похідна 1 ) √3 - (− 1 ) √3 (− 0 Поведінка функції 1 ) √3 0 -0,5 -0,5 7) Асимптоти y=kx+b – рівняння асимптоти 𝑦(𝑥) 𝑥→±∞ 𝑥 𝑘 = lim 𝑏 = lim (𝑦(𝑥) − 𝑘𝑥) 𝑥→±∞ 𝑥2 1 − 𝑥 −1 𝑥 −1 𝑥3 𝑥3 = 0 𝑘 = lim = lim = lim 𝑥→±∞ 𝑥(𝑥 2 + 1) 𝑥→±∞ 𝑥 3 + 𝑥 𝑥→±∞ 𝑥 3 𝑥 + 𝑥3 𝑥3 2 𝑥2 1 𝑥 −1 2− 2 𝑏 = lim 2 = lim 𝑥 2 𝑥 = 1 𝑥→±∞ 𝑥 + 1 𝑥→±∞ 𝑥 1 + 𝑥2 𝑥2 2 y=1 – горизонтальна асимптота. 8) Знайдемо додаткові точки і побудуємо графік у(-3)=у(3)=0,8 ( перегин 1 2 ) − 1 −2 1 1 √3 у(± ) = = 3 =− 2 4 2 1 √3 (± ) + 1 3 √3 у(-2)=у(2)=0,6 1 ) √3 √3 + , перегин (± 2 1 ( 1 √3 , +∞) - 6.7 Дослідити функцію , яка задана параметрично 𝑥 = 𝑡 2 , 𝑦 = 𝑡 3 та побудувати графік. Розв’язання: 1) ОВФ y(t) існує для будь-яких 𝑡 ∈ (−∞, +∞) x(t) існує для будь-яких t∈(-∞,+∞) Вертикальних асимптот і точок розриву немає. 2) Точки перетину графіка з осями координат: x=0, якщо t=0, тому 𝑦 = 0 . Графік проходить через початок координат. 3) Періодичність та парність/непарність у(t) – неперіодична функція, x(t) – неперіодична функція, 𝑥(−𝑡) = 𝑡 2 = 𝑥(𝑡) - парна функція 𝑦(−𝑡) = −𝑡 3 = −𝑦(𝑡) – непарна функція 𝑦2 = 𝑥3, 3 𝑥 = √𝑦 2 , 3 𝑥(−𝑦) = √𝑦 2 = 𝑥(𝑦) – парна функція, графік симетричний відносно осі ОX 4) Точок розриву немає, функція монотонна. 5) Інтервали монотонності, екстремуми 𝑥 ′ (𝑡) = 𝑑𝑥 у′ (𝑡) = 𝑑𝑦 ′ (𝑥) у 𝑑𝑡 𝑑𝑡 = 2𝑡, 𝑥 ′ = 0, 2𝑡 = 0, 𝑡 = 0 = 3𝑡 2 , 𝑦 ′ = 0, 3𝑡 2 = 0, 𝑡 = 0 𝑑𝑦 𝑑𝑦 𝑑𝑡 3𝑡 2 3𝑡 = = = = 𝑑𝑥 𝑑𝑥 2𝑡 2 𝑑𝑡 𝑑𝑦 Область зміни t Відповідна область зміни х Відповідна область зміни у Знак 𝑑𝑥 t<0 x<0 y<0 - t>0 x>0 y>0 + 6) Інтервали опуклості 𝑥 ′′ (𝑡) = у′ ′(𝑡) = 𝑑2 𝑥 𝑑𝑡 2 𝑑2 𝑦 𝑑𝑡 2 = 2, 𝑥 ′′ = 2, = 6𝑡, 𝑦 ′′ = 0, 6𝑡 = 0, 𝑡 = 0 𝑑2 𝑦 2 𝑑 𝑦 2 6𝑡 у′ ′(𝑥) = 2 = 𝑑𝑡2 = = 3𝑡 𝑑 𝑥 𝑑𝑥 2 𝑑𝑡 2 Характер зміни у(х) Область зміни t t<0 Відповідна область зміни х x<0 Відповідна область зміни у y<0 x>0 y>0 t>0 7) Асимптоти y=kx+b – рівняння асимптоти 𝑦(𝑥) 𝑥→±∞ 𝑥 𝑘 = lim 𝑏 = lim (𝑦(𝑥) − 𝑘𝑥) 𝑥→±∞ ±√𝑥 3 = lim (±√𝑥) = ± ∞ 𝑥→±∞ 𝑥→±∞ 𝑥 𝑘 = lim 𝑏 = lim (±√𝑥 3 ± ∞) = ±∞ 𝑥→±∞ Похилих та горизонтальних асимптот немає. 8) Знайдемо додаткові точки і побудуємо графік t=1, у(1)=x(1)=1 t=-1, у(-1)=-1, x(-1)=1 t=2, у(2)=8, x(2)=4 t=-2, у(-2)=8, x(-2)=4 Знак + 𝑑2 𝑦 𝑑𝑥 2 Характер зміни у(х) 6.7 Дослідити неявно задану функцію, перейшовши до полярної системи координат. (𝑥 2 + 𝑦 2 )2 = 3𝑥 2 − 𝑦 2 Розв’язання: 1) Перейдемо до полярних координат: 𝑥 = 𝜌𝑐𝑜𝑠𝜑. 𝑥 2 = 𝜌2 𝑐𝑜𝑠 2 𝜑 𝑦 = 𝜌𝑠𝑖𝑛𝜑, 𝑦 2 = 𝜌2 𝑠𝑖𝑛2 𝜑 𝑥 2 + 𝑦 2 = 𝜌2 𝑐𝑜𝑠 2 𝜑 + 𝜌2 𝑠𝑖𝑛2 𝜑 = 𝜌2 . Досліджуване рівняння прийме вигляд: 𝜌4 = 3𝜌2 𝑐𝑜𝑠 2 𝜑 − 𝜌2 𝑠𝑖𝑛2 𝜑 𝜌2 = 3𝑐𝑜𝑠 2 𝜑 − 𝑠𝑖𝑛2 𝜑 𝜌2 = 3(1 − 𝑠𝑖𝑛2 𝜑) − 𝑠𝑖𝑛2 𝜑 𝜌2 = 3 − 3𝑠𝑖𝑛2 𝜑 − 𝑠𝑖𝑛2 𝜑 𝜌2 = 3 − 4𝑠𝑖𝑛2 𝜑 𝜌1 = −√3 − 4𝑠𝑖𝑛2 𝜑 𝜌2 = √3 − 4𝑠𝑖𝑛2 𝜑 Відомо, що 𝜌≥0 тому досліджувати будемо функцію 𝜌(𝜑) = √3 − 4𝑠𝑖𝑛2 𝜑 2) ОВФ 3 − 4𝑠𝑖𝑛2 𝜑 ≥ 0 4𝑠𝑖𝑛2 𝜑 ≤ 3 𝑠𝑖𝑛2 𝜑 ≤ 𝑠𝑖𝑛𝜑 ≤ 𝜑 ≤ (−1)𝑘 𝑎𝑟𝑐𝑠𝑖𝑛 𝜑 ≤ (−1)𝑘 ∙ 3 4 √3 2 √3 + 2𝜋𝑘, 𝑘𝜖𝑍 2 𝜋 + 2𝜋𝑘, 𝑘𝜖𝑍 3 𝜋 𝜋 2𝜋 4𝜋 𝜌(𝜑) на інтервалі (0,2𝜋) існує в інтервалах (− , ) і ( , ). 3 3 3 3 Схематично, покажемо у вигляді заштрихованих області, в яких функція не існує. 3) 𝜌(𝜑) – періодична функція з періодом 2π. 𝜌(−𝜑) = √3 − 4𝑠𝑖𝑛2 (−𝜑) = √3 − 4𝑠𝑖𝑛2 𝜑 = 𝜌(𝜑) симетричний відносно осі ОУ. – функція парна, тому її графік 4) Точки перетину графіка з осями координат: Для φ=0, 𝜌(𝜑) = √3 . Для ρ=0, 𝜑 = (−1)𝑘 ∙ 𝜋 + 2𝜋𝑘, 𝑘𝜖𝑍 3 Таким чином, вісь ОХ графік перетинає в точках (−√3, 0) та (√3, 0), вісь ОУ графік перетинає в точці (0,0) і графік проходить через початок координат. 5) Інтервали монотонності, екстремуми 𝜌′ (𝜑) = −8𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑 2√3 − 4𝑠𝑖𝑛2 𝜑 = −2𝑠𝑖𝑛2𝜑 √3 − 4𝑠𝑖𝑛2 𝜑 𝜌′ = 0 при умові, що −2𝑠𝑖𝑛2𝜑 √3−4𝑠𝑖𝑛2 𝜑 = 0, 𝑠𝑖𝑛2𝜑 = 0, 2𝜑 = 𝜋𝑘, 𝑘𝜖𝑍 𝜋 𝜑 = 𝑘, 𝑘𝜖𝑍 2 Оскільки графік симетричний відносно осі ОУ, то достатньо визначитись з поведінкою функції на інтервалі 𝜋 𝜋 (− , ). 3 3 𝜌′ не існує при умові, що √3 − 4𝑠𝑖𝑛2 𝜑 ≤ 0, 𝜑 ≥ (−1)𝑘 ∙ 𝜋 + 2𝜋𝑘, 𝑘𝜖𝑍 3 Дослідимо знаки похідної на інтервалах 𝜋 (− 3 , 0) 𝜋 𝜌 (− 4 ) = 𝜋 𝜌′ ( 4 ) = (0, 3 ) 𝜋 4 2 sin(2∙ ) 𝜋 ′ 𝜋 4 √3−4𝑠𝑖𝑛2 (− ) 𝜋 4 𝜋 2 √3−4𝑠𝑖𝑛 ( ) 4 −2 sin(2∙ ) = 2 > 0, = −2 < 0, Інтервали монотонності матимуть вигляд: 𝜋 інтервали 𝜋 (− 3 , 0) 0 (0, 3 ) + 0 - Похідна Поведінка функції Max, √3 Таким чином, на графіку маємо коло з центром в точці (0,0) і радіусом √3 , що обмежує графік функції. 6) Інтервали опуклості та точки перегину 𝜌′′ (𝜑) = ( −2𝑠𝑖𝑛2𝜑 √3 − 4𝑠𝑖𝑛2 𝜑 = −2 𝑠𝑖𝑛2𝜑 ∙ (−8𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑) 2√3 − 4𝑠𝑖𝑛2 𝜑 = 3 − 4𝑠𝑖𝑛2 𝜑 2𝑐𝑜𝑠2𝜑 ∙ √3 − 4𝑠𝑖𝑛2 𝜑 − / ) = −2 2𝑐𝑜𝑠2𝜑 ∙ (3 − 4𝑠𝑖𝑛2 𝜑) − 𝑠𝑖𝑛2𝜑 ∙ (−2𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑) √3 − 4𝑠𝑖𝑛2 𝜑(3 − 4𝑠𝑖𝑛2 𝜑) = −4 = 3𝑐𝑜𝑠2𝜑 − 4𝑠𝑖𝑛2 𝜑𝑐𝑜𝑠2𝜑 + 𝑠𝑖𝑛2 2𝜑 √3 − 4𝑠𝑖𝑛2 𝜑(3 − 4𝑠𝑖𝑛2 𝜑) Виразимо чисельник через cosφ, застосовуючи тригонометричні тотожності: 3𝑐𝑜𝑠2𝜑 = 6 cos 2 𝜑 − 3 −4𝑠𝑖𝑛2 𝜑𝑐𝑜𝑠2𝜑 = −4(1 − 𝑐𝑜𝑠 2 𝜑)(2𝑐𝑜𝑠 2 𝜑 − 1) = 8𝑐𝑜𝑠 4 𝜑 − 12𝑐𝑜𝑠 2 𝜑 + 4 𝑠𝑖𝑛2 2𝜑 = 1 − 𝑐𝑜𝑠 2 2𝜑 = 1 − (2𝑐𝑜𝑠 2 𝜑 − 1)2 = 4𝑐𝑜𝑠 2 𝜑 − 4𝑐𝑜𝑠 4 𝜑 Чисельник матиме вигляд 3𝑐𝑜𝑠2𝜑 − 4𝑠𝑖𝑛2 𝜑𝑐𝑜𝑠2𝜑 + 𝑠𝑖𝑛2 2𝜑 = == 6 cos 2 𝜑 − 3 + 8𝑐𝑜𝑠 4 𝜑 − 12𝑐𝑜𝑠 2 𝜑 + 4 + 4𝑐𝑜𝑠 2 𝜑 − 4𝑐𝑜𝑠 4 𝜑 = = 4𝑐𝑜𝑠 4 𝜑 − 2𝑐𝑜𝑠 2 𝜑 + 1 𝜌′′ = 0, якщо 4𝑐𝑜𝑠 4 𝜑 − 2𝑐𝑜𝑠 2 𝜑 + 1 = 0 Чисельник не може дорівнювати 0, тому точок перегину немає. Оцінимо поведінку функції на інтервалі 𝜋 𝜋 (− , ). 3 3 ′′ 𝜌 = 𝜌′′ (0) = 4−2+1 √(3−0)3 = 3 √27 4𝑐𝑜𝑠 4 𝜑 − 2𝑐𝑜𝑠 2 𝜑 + 1 √(3 − 4𝑠𝑖𝑛2 𝜑)3 > 0 - вогнута 7) Знайдемо додаткові точки і побудуємо графік 𝜋 𝜋 1 2 2 𝜌 (± ) = √3 − 4𝑠𝑖𝑛 (± ) = √3 − 4 ∙ ( ) = 1 4 4 √2 𝜋 𝜋 1 2 2 √ 𝜌 (± ) = √3 − 4𝑠𝑖𝑛 (± ) = 3 − 4 ∙ ( ) = √2 6 6 2