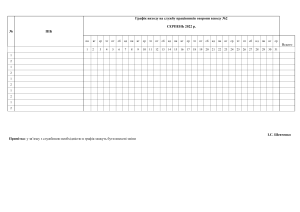
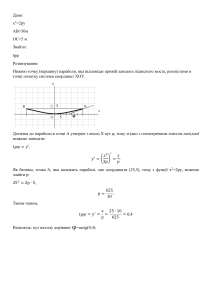
БУДЬОННІВСЬКА РАЙОННА У М. ДОНЕЦЬКУ РАДА ВІДДІЛ ОСВІТИ ДОНЕЦЬКА ЗАГАЛЬНООСВІТНЯ ШКОЛА І-ІІІ СТУПЕНІВ № 120 ДОНЕЦЬКОЇ МІСЬКОЇ РАДИ ДОНЕЦЬКОЇ ОБЛАСТІ Урок «Квадратична функція у=ах2+вх.+с, (а≠0), її графік і властивості.» 9 клас Підготував: учитель математики Н.П. Чешковська Епіграф уроку: «Перед людиною до розуму три шляхи: шлях роздумів- найшляхетніший, шлях наслідування –найлегший шлях, шлях особистого досвіду – найтяжчий шлях» Конфуцій Мета уроку: навчальна: - систематизувати та узагальнювати матеріал, опрацьований на попередніх уроках, повторити, уточнити нові поняття; - систематизувати та узагальнювати знання, отримані учнями в процесі вивчення теми. розвивальна: - розвивати увагу, мислення, пам'ять, культуру математичного мовлення; - вміння працювати самостійно, в парах, вміння спілкуватися, допомагати іншим, аналізувати ситуацію, оцінювати свої дії та дії інших учнів; - вміння і навички щодо розв'язування завдань та їх оформлення; - продовжувати розвивати загальноосвітні навички; - сприяти розвитку комунікативної, інформаційної, соціальної, полікультурної компетентностей, а також самоосвіти й саморозвитку продуктивної творчої діяльності. виховна: - виховувати уважність, кмітливість, акуратність, самостійність, дисциплінованість, самокритичність. працьовитість, Тип уроку: узагальнення та систематизація знань, умінь, навичок. Методи: словесні: розповідь, бесіда, використання ключових слів, коментар до використання вправ, самооцінка, взаємонавчання, методи мотивації, збудження інтересу; наочні: робота з роздавальним матеріалом, бланк самооцінювання. практичні: розв'язування вправ, самостійна робота, робота в парах, метод повторення, поступового ускладнення завдань. Оцінюється: рівень навчальних досягнень учнів. Організаційно-психологічна частина. Підготовка до свідомої навчальної праці: постановка мети, актуалізація опорних знань, умінь. Обладнання: картки з індивідуальними завданнями, комп'ютер, таблиці. Мультимедійна презентація, створена засобами POWER POINT (додаток 1). ХІД УРОКУ І.Організаційний момент Учитель вітається з учнями та перевіряє готовність до уроку. ІІ. Мотивація навчальної діяльності Сьогодні ми підіб’ємо підсумки вивчення теми «Квадратична функція у=ах2+вх.+с, (а≠0), її графік і властивості». Я сподіваюсь на успішну працю, що на уроці ми зможете показати свої знання вміння, кмітливість, то ж будьте уважними, думайте, запитуйте, пропонуйте, оскільки нам разом з вами йти шляхом до істини. Я хочу,щоб на цьому уроці ви показали наскільки ви компетентні в даній темі, тобто як ви володієте необхідною інформацією і вмієте застосувати набуті знання і досвід. Сьогодні на уроці алгебри ми будемо працювати разом і розраховую на вашу підтримку та допомогу. Кожному з вас хочу побажати,щоб на цьому уроці ви були «У»- успішними «С» - спокійними «П» - прогресивними «І» - ініціативними «Х» - хоробрими У класі ви розмістилися попарно, тому протягом уроку, якщо є бажання, можна всі питання обговорювати в парах. Підготуємо наші зошити до роботи. Пам’ятайте, що під час роботи з діловою документацією,її треба вести старанно, охайно, уважно ставитися до цієї справи. ІІІ.Актуалізація опорних знань Узагальнення і повторення раніше здобутих знань Розминка Рис.1 рис2. 1.Дайте означення квадратичної функції 2.Що є графіком квадратичної функції 3.Як визначити напрям гілок параболи? 4.Можливі способи побудови графіка функції у=ах2+вх.+с, (а≠0) 5.Назвіть формули для обчислення вершин параболи 6.Вісь симетрії параболи 7.Як знайти точки перетину параболи з осями координат 8.Назвіть область визначення функції (а>0) 9. Назвіть область визначення функції (а<0) 10.Назвіть проміжки зростання та спадання функцій (а>0) 11. Назвіть проміжки зростання та спадання функцій (а<0) Рис.3 Рис.4 12.Назвіть проміжки знак осталості функцій (рис. 3) 13.Нулі функції рис.3 14.Назвіть проміжки знак осталості функцій (рис. 4) 15.Нулі функції рис.4 ІV. Актуалізація знань і навичок Конкурс знавців квадратичної функції Учням пропонуються графіки квадратичних функцій, і за цими графіками треба відповісти на запитання: 1.вказати знак першого коефіцієнта; 2.вказати знак дискримінанта; 3. вказати, чому дорівнює знак вільного члену. Конкурс графоманів Встановіть відповідність між графіками функцій і формулами, які їх задають 1) у= х2-4 2) у= х2 + 4 3) у= 4 – х2 4) у= (х-4)2 5) у= (х- 4)2 -2 6) у= (х- 2)2 + 4 Відповідь. Запишіть двоцифровими числами: 1-ша цифра – номер функції; 2-га цифра - номер відповідного графіка Починаємо працювати У кого не вийшло – не хвилюйтесь, люди вчаться на своїх помилках V. Закріплення вмінь та навичок (Практикум. Розв’язування стандартної задачі) № 1. Побудуйте графік функції у= 3х-2х-х2 Користуючись графіком, знайдіть: А) множину значень функції; Б) проміжок, на якому функція спадає В) при яких значеннях х функція набуває додатих значень Розв’язування цікавої задачі №2. Малюємо графіками функцій: 3 при -5 ≤ х < - 2; (капелюх жовтого кольору, кольор віри та оптимузму ) у= - х2 + 7 при – 2 ≤ х ≤ 2; 3 при 2 ≤ х < 2 Розв’язування нестандартних вправ. Приклад № 3 Побудуйте графік функції У= (ОДЗ) х2 - 16 х2 - 4 Приклад № 4 На рисунку зображено графік квадратичної функції у=ах2+вх.+с, визначте знак кожного з параметрів а,в,с. у=ах2+вх.+с Рис7. Приклад № 5 Побудуйте параболу У= │х2 - 6х + 5│ VІ. Домашні завдання. Самостійна робота в 4 варіантах (додаток 2) VII. Підсумки уроку Закінчуючи урок, хочу подякувати вам за знання, вміння, способи діяльності, рецепти досягнення успіху. Діти на початку уроку я Вам запропонувала бути - успішними - спокійними - прогресивними - ініціативними - хоробрими Якими ви почували себе на цьому уроці. Діти оголошують картку самооцінки. З вашої самооцінки бачу, що кожен з вас досяг успіху. Хочу щоб Ви зрозуміли, що бажала я всім вам «Успіху». Успіх в розглянутій нами теми це і є ваша компетентність, ви володієте необхідною інформацією і вмієте застосовувати набуті знання і досвід. Емблемою нашого уроку обираю наш капелюшок жовтого кольору, кольору віри та оптимізму. Тому хочу подякувати вам за урок, ще раз побажати успіху, сказати,що я вірю у ваш успіх. На згадку про наш урок візьміть капелюшок з іще одним рецептом успіху. «Успіх це тільки 10 % таланту і 90% щоденної наполегливої праці.» Додаток 2 I варіант Виберіть правильний варіант відповіді 1 2 1. На якому з малюнків зображено графік функції у= x ? 3 y y 1 1 x 0 1 а) y 0 1 б) 3 2 1 x 0 в) y 1 x x 0 1 2 3 г) 2. Графік функції у=х2 +7 отримано з графіка функції у= х2: а) зсувом вгору на 7 одиниць; б) зсувом праворуч на 7 одиниць; в) зсувом ліворуч на 7 одиниць; г) зсувом вниз на 7 одиниць; 3. Знайдіть корені квадратного тричлена х2+7х+12. а) х1=6; х2=4; б) х1= – 5; х2=7; в) х1=3; х2= 4; г) х1= – 3; х2= – 4. 4. При яких значеннях b графік функції y=3x2+bx– 2 проходить через точку D(–1;5)? а) b=4; б) b=7; в) b= – 4; г) b= 5. Учень 9 класу ______________________________________ ( Прізвище, Ім’я ) А 1 2 3 4 Б В Г II варіант Виберіть правильний варіант відповіді 2 1. На якому з малюнків зображено графік функції у= x ? y 1 0 y 1 0 1 x -1 а) y 1 x y 0 1 б) 1 0 x в) x -1 г) 2. Графік функції у=х2 – 2 отримано з графіка функції у= х2: а) зсувом вгору на 2 одиниці; б) зсувом праворуч на 2 одиниці; в) зсувом ліворуч на 2 одиниці; г) зсувом вниз на 2 одиниці. 3. Знайдіть корені квадратного тричлена х2 – 8х – 9 . а) х1=9; х2= – 1; б) х1= – 5; х2=7; в) х1=3; х2= - 9; г) х1= – 3; х2= – 4. 4. Чи проходить графік функції y=x2– 5x+6 через точку А(–3;14)? а) можливо так, а можливо й ні; б) ні; в) так; г) не можна сказати. Учень 9 класу ______________________________________ ( Прізвище, Ім’я ) А 1 2 3 4 Б В Г ІІI варіант Виберіть правильний варіант відповіді 2 1. На якому з малюнків зображено графік функції у=2 x ? y 2 1 0 1 y 2 1 x y 2 1 x 0 1 а) y 1 x 0 1 2 1 б) x 0 в) г) 2. Графік функції у=3х2 – 1 отримано з графіка функції у= 3х2: а) зсувом вгору на 1 одиницю; б) зсувом праворуч на 1 одиницю; в) зсувом ліворуч на 1 одиницю; г) зсувом вниз на 1 одиницю. 3. Знайдіть корені квадратного тричлена х2– 7х– 8. а) х1=9; х2=1; б) х1= 8; х2= - 1; в) х1=3; х2= – 9; г) х1= – 3; х2= – 4. 4. Чи проходить графік функції y=x2– 7x+6 через точку В(–1;14)? а) можливо так, а можливо й ні; б) ні; в) так; г) не можна сказати. Учень 9 класу ______________________________________ ( Прізвище, Ім’я ) А 1 2 3 4 Б В Г IV варіант Виберіть правильний варіант відповіді 3 1. На якому з малюнків зображено графік функції у= ? y y y x 1 0 3 2 1 0 1 23 x 12 3 а) 3 2 1 x 0 1 23 x б) в) 3 3 2. Графік функції у= – 4 отримано з графіка функції у= : x x y 3 -1 x 0 г) а) зсувом вгору на 4 одиниці; б) зсувом праворуч на 4 одиниці; в) зсувом ліворуч на 4 одиниці; г) зсувом вниз на 4 одиниці. 3. Знайдіть корені квадратного тричлена х2+10х– 11. а) х1=–11; х2=1; б) х1= – 5; х2=7; в) х1=11; х2= – 1; г) х1= – 3; х2= – 4. 4. При яких значеннях b графік функції y=x2– bx– 2 проходить через точку С(1;4)? а) b=4; б) b=7; в) b= – 5; г) b= 5. Учень 9 класу ______________________________________ ( Прізвище, Ім’я ) А 1 2 3 4 Б В Г