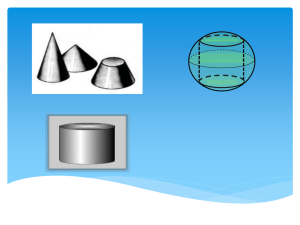
Конус-это объемная геометрическая фигура, образованная при помощи вращения Пирамиды по ее оси. Точку S называют вершиной конуса. Отрезок SO называют осью конуса. Расстояние от точки S до плоскости α (длину отрезка SO) называют высотой конуса. Круг с центром в точке O, лежащий на плоскости α, называют основанием конуса, радиус этого круга называют радиусом основания конуса, а саму плоскость α называют плоскостью основания конуса. Отрезки, соединяющие точку S с точками окружности, называют образующими конуса. Совокупность всех образующих конуса составляет боковую поверхность конуса (коническую поверхность). Полная поверхность конуса состоит из основания конуса и его боковой поверхности. Замечание. Все образующие конуса имеют одинаковую длину. У конуса с высотой h и радиусом основания r длина образующих равна (L) Формулы для объема, площади боковой и полной поверхности Sосн = πr2, Sбок= πrl Sполн = πr2 + πrl Усеченный конус образован путем вращения прямоугольной трапеции по ее оси R – радиус большего основания конуса, являющегося кругом, с центром в точке O1 и диаметром AD. r – радиус меньшего основания конуса с центром в точке O2, диаметр – отрезок BC. h (O1O2) – высота конуса; одновременно является высотой трапеции ABCD и осью симметрии обеих фигур. l (AB, CD и т.д.) – образующие конуса; это отрезки, соединяющие две точки на окружностях двух его оснований (с минимально возможным расстоянием). Одновременно являются боковыми сторонами трапеции (осевого сечения конуса). Осевое сечение усеченного конуса – это равнобедренная трапеция ABCD, образованная в результате пересечения конуса плоскостью, проходящей через его ось. Поверхность усеченного конуса – боковая поверхность и поверхность двух его оснований Формулы для объема, площади боковой и полной поверхности Sбок= π (r + r1)l ,