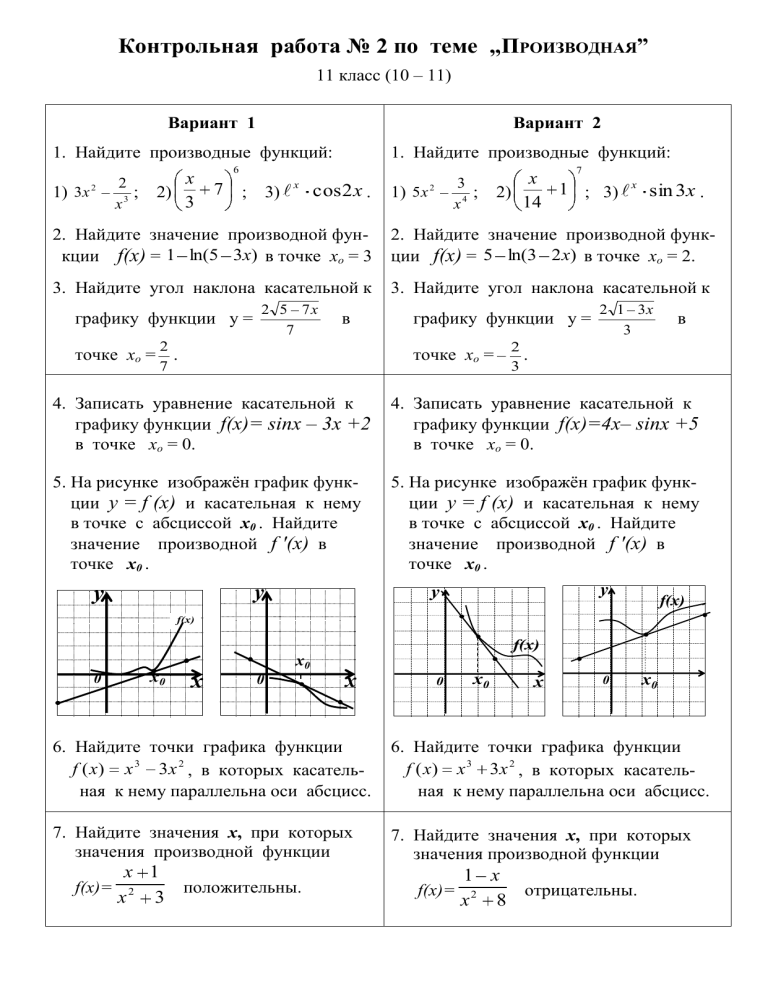
Контрольная работа № 2 по теме ,,ПРОИЗВОДНАЯ” 11 класс (10 – 11) Вариант 1 Вариант 2 1. Найдите производные функций: 1) 3x 2 2 ; x3 x 2) 3 1. Найдите производные функций: 6 7 7 ; 3) x cos 2 x . 3 ; x4 1) 5 x 2 x 1 ; 3) x sin 3x . 2) 14 2. Найдите значение производной функции f(х) = 1 ln(5 3x) в точке хо = 3 2. Найдите значение производной функции f(х) = 5 ln(3 2 x) в точке хо = 2. 3. Найдите угол наклона касательной к 3. Найдите угол наклона касательной к графику функции у = 2 5 7x 7 в 2 7 точке хо = . графику функции у = точке хо = 2 1 3x 3 в 2 . 3 4. Записать уравнение касательной к графику функции f(х)= sinx – 3x +2 в точке хо = 0. 4. Записать уравнение касательной к графику функции f(х)=4х– sinx +5 в точке хо = 0. 5. На рисунке изображён график функции у = f (x) и касательная к нему в точке с абсциссой х0 . Найдите значение производной f '(x) в точке х0 . 5. На рисунке изображён график функции у = f (x) и касательная к нему в точке с абсциссой х0 . Найдите значение производной f '(x) в точке х0 . y y y y f(x) f(x) f(x) x0 0 x0 x 0 x 0 x0 x 0 x0 6. Найдите точки графика функции f ( x) x 3 3x 2 , в которых касательная к нему параллельна оси абсцисс. 6. Найдите точки графика функции f ( x) x 3 3x 2 , в которых касательная к нему параллельна оси абсцисс. 7. Найдите значения х, при которых значения производной функции 7. Найдите значения х, при которых значения производной функции x 1 f(х)= 2 положительны. x 3 f(х)= 1 x отрицательны. x2 8