МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«Харьковский политехнический институт»
А. Н. Огурцов
ФЕРМЕНТАТИВНЫЙ КАТАЛИЗ
Учебное пособие
для студентов направления подготовки
051401 «Биотехнология»,
в том числе для иностранных студентов
Утверждено
редакционно-издательским
советом университета,
протокол № 1 от 24.06.2010 г.
Харьков НТУ «ХПИ» 2010
ББК 28.07
О 39
УДК 577.15
Рецензенты:
В. В. Давыдов, д-р. мед. наук, проф., зав. лаб. возрастной эндокринологии
и обмена веществ ГП "Институт охраны здоровья детей
и подростков АМН Украины"
Ю. В. Малюкин, д-р физ.-мат. наук, проф., зав. отд. нанокристаллических
материалов, зам. директора ИСМ НАН Украины
ВСТУПЛЕНИЕ
Навчальний посібник містить матеріали з основних питань ферментативного каталізу відповідно до програми підготовки студентів напряму
«Біотехнологія».
Призначено для студентів спеціальностей біотехнологічного профілю всіх
форм навчання.
Огурцов, А. Н.
О 39
Ферментативный катализ [Текст] : учеб. пособие / А. Н. Огурцов.
– Харьков : НТУ «ХПИ», 2010. – 304 с. – На рус. яз.
ISBN 978-966-593-843-9
Учебное пособие содержит материалы по основным вопросам ферментативного катализа в соответствии с программой подготовки студентов направления
«Биотехнология».
Предназначено для студентов специальностей биотехнологического профиля всех форм обучения.
Ил. 147.
Табл. 11.
Библиогр.: 29 назв.
ББК 28.07
ISBN 978-966-593-843-9
Ферментативные процессы являются основой биотехнологических
производств любой сложности. Биохимические преобразования под
управлением ферментов определяют как спектр получаемых продуктов
реакций, так и эффективность биотехнологического производства в целом. Сознательное управление сложными метаболическими процессами,
определяющими эффективность конкретного производства, требует от
биотехнолога как четкого представления физических явлений и принципов молекулярных аспектов функционирования ферментов, лежащих в
основе конкретного регламента, так и владения основами феноменологического анализа кинетики ферментативных реакций.
Предметом учебной дисциплины "Ферментативный катализ" являются биофизические и биохимические механизмы ферментативных процессов в живой клетке, и методы контроля и управления скоростью
протекания и специфичностью биокаталитических процессов. Курс
"Ферментативный катализ" состоит из трех разделов: теоретические основы биокатализа, механизмы ферментативных процессов и кинетика
ферментативных реакций.
Настоящее пособие вместе с пособием "Введение в биофизику: Физические основы биотехнологии" составляют теоретические основы последующего изучения таких курсов, как "Молекулярная биология",
© А.Н. Огурцов, 2010
3
Промышленная биотехнология", "Бионанотехнология", "Биологические
мембраны" и "Молекулярная биотехнология".
Научную основу курса "Ферментативный катализ" составляют физика, биохимия, биоколлоидная химия и биофизическая химия. Методическими основами курса являются лекции, в которых излагаются
основные положения каждого раздела, практические занятия и самостоятельная работа студентов, являющаяся основным способом усвоения материала в свободное от аудиторных занятий время.
Для самостоятельной работы выделяется больше половины общего
объема времени, предназначенного для изучения данной дисциплины.
Самостоятельная работа проводится по всем темам, входящим в дисциплину. В процессе самостоятельной работы студент учится самостоятельно
приобретать знания, которые затем используются в ходе выполнения индивидуального задания, практических занятий, при подготовке к выполнению контрольных работ и к экзамену.
Настоящее пособие подготовлено на основе адаптированных работ
[1–21], послуживших также источником иллюстраций, таким образом,
чтобы максимально облегчить усвоение курса "Ферментативный катализ"
студентам направления подготовки 051401 "Биотехнология". Перед работой с пособием следует внимательно изучить материал пособия [1], без
которого невозможно понимание явлений, определяющих биофизику
ферментативных процессов на молекулярном уровне.
В конце каждой главы приведены контрольные вопросы и задачи,
самостоятельная проработка которых облегчит усвоение курса "Ферментативный катализ" студентам направления подготовки 051401 "Биотехнология".
РАЗДЕЛ I
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ БИОКАТАЛИЗА
Жизнедеятельность организмов представляет собой одновременное
и согласованное функционирование огромного количества ферментов, их
ассоциатов и комплексов в различных клетках, тканях и органах организма, которые осуществляют метаболические преобразования и преобразуют энергию, создавая в результате своего функционирования
необходимые метаболиты, силы и потоки. Для описания сложных неравновесных процессов, обеспечивающих функционирование ферментов, необходимо сначала корректно определить фундаментальные физические и
физико-химические понятия и постулаты, на которых будет основываться
дальнейшее изложение.
Глава 1
КАТАЛИЗ И БИОКАТАЛИЗ
1.1. ОСНОВНЫЕ ПОНЯТИЯ ЭНЗИМОЛОГИИ
Ферменты (от латинского fermentum – закваска), энзимы (от греческого en – "в" и zyme – "закваска") или биокатализаторы, – это вещества
биологического происхождения, ускоряющие химические реакции.
Для того чтобы не смешивать слова различных языков, принято называть науку, изучающую ферменты и катализируемые ими реакции, энзимологией (от греческих слов en, zyme, logos).
4
5
Организованная последовательность процессов обмена веществ –
метаболизм – возможна при условии, что каждая клетка обеспечена собственным генетически заданным набором ферментов. В живой клетке
множество разнообразных соединений, но реакции между ними не беспорядочны, а образуют строго определенные, характерные для данной клетки метаболические пути – согласованные последовательности реакций.
Индивидуальность клетки в большой степени определяется уникальным набором ферментов, который она генетически запрограммирована производить. Нехватка какого-либо фермента или какой-нибудь его
дефект могут иметь очень серьезные отрицательные последствия для организма. Регуляция метаболических процессов ферментами обеспечивает
соответствие обмена веществ измененным условиям.
Почти все ферменты являются белками. Однако, известны также каталитически активные нуклеиновые кислоты – рибозимы.
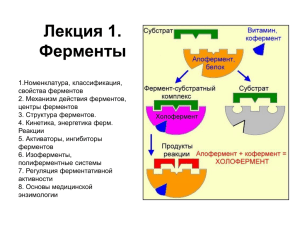
Вещество, на которое действует фермент, называется субстратом
(от латинского substratum – подстилка, основа).
Существуют сложные двух- и многокомпонентные ферменты, содержащие как белковые, так и небелковые компоненты.
Апоферментом (apoenzyme) называется белковый компонент такого
сложного фермента.
Кофактором (cofactor) называется небелковый компонент сложного фермента.
Ферментативной активностью обладает только комплекс апофермент-кофактор, который называется холоферментом (holoenzyme)
Апофермент + кофактор = холофермент.
Кофакторы можно разделить на две группы:
1) металлы (как правило – ионы металлов Zn2+, Mg2+, Mn2+, Fe2+,
Cu2+, K+, Na+),
2) сложные органические соединения.
Органические небелковые кофакторы называются коферментами
(coenzymes). Источником коферментов часто служат витамины.
6
Тип связи между ферментом и коферментом может быть различным. Иногда они существуют отдельно и связываются друг с другом во
время протекания реакции. Многие коферменты легко отделяются от холофермента и служат переносчиками отдельных атомов или групп атомов, отщепляемых ферментом от субстрата.
В других случаях кофактор и фермент связаны постоянно и иногда
прочными ковалентными связями. В последнем случае небелковая часть
фермента называется простетической группой (prosthetic group).
1.2. СПЕЦИФИКА БИОКАТАЛИЗАТОРОВ
Ферменты отличаются от других катализаторов тремя уникальными свойствами:
• высокой эффективностью действия,
• специфичностью действия,
• способностью к регуляции.
Скорость ферментативных реакций обычно в 106–1012 раз выше, чем
скорость соответствующих неферментативных реакций. Пример эффективности протекания реакции разложения перекиси водорода с участием
фермента каталазы приведен в таблице 1.
Таблица 1 – Эффективность протекания реакции разложения перекиси водорода
Относительная скорость реакЭнергия активации 2H 2 O 2 → 2H 2 O + O 2
Катализатор
ции, кДж/моль
при 300 К
Без катализатора
70
1
Pt (гетерогенный)
45
2 ⋅ 103
Ионы железа (гомогенный)
42
8 ⋅ 103
Каталаза (фермент)
7
9 ⋅ 1010
7
Активность фермента измеряется в международных единицах
(МЕ), соответствующих активности, превращающей 1 микромоль субстрата в минуту, или, как это было введено в 1973 году, в каталах (кат),
соответствующих активности, превращающей 1 моль субстрата в секунду.
Удельная активность выделенного фермента выражается в единицах
активности на единицу массы активного белка. Связь МЕ с каталом:
аргинин (Arg) или лизин (Lys) (рисунок 1). Тромбин (EC 3.4.21.5) – фермент, который участвует в процессе сворачивании крови, разрывает только аргинин-глицин (Arg-Gly) связь в определенной пептидной
последовательности.
1 кат = 1 моль субстрата/с = 60 моль/мин = 60⋅106 мкмоль/мин = 6⋅107 МЕ,
1 МЕ = 1 мкмоль/мин = 1/60 мкмоль/с = 1/60 мккат = 16,67 нкат.
Другие соотношения, используемые в энзимологии:
Число молей превращенного субстрата
,
мин
Число каталов
,
Удельная активность =
Масса активного белка, кг
Число оборотов =
Молярная активность =
Число каталов
.
Число молей фермента
Специфичность действия – способность выбирать определенный
субстрат и катализировать строго специфическую реакцию.
Для ферментов характерны:
а) высокая субстратная специфичность – даже если какая-то реакция может идти с разными соединениями, данный фермент будет
работать только с одним субстратом,
б) специфичность пути превращения (специфичность по типу реакции) – данный фермент катализирует только ту реакцию, для которой он предназначен. Например, фермент декарбоксилаза,
отщепляющий карбоксильную группу аминокислоты, не будет
отщеплять аминогруппу той же аминокислоты. Для этого есть
фермент трансаминаза.
Так, например, трипсин (EC 3.4.21.4) катализирует разрыв пептидной связи только с карбоксильной стороны от аминокислотных остатков
8
а
б
Рисунок 1 – Специфичность ферментов: а – трипсин разрывает связь со стороны карбоксильной группы от аргинина или лизина, б – тромбин специфично разрывает связь аргинин-глицин
Другой пример высокоспецифичного ферментного катализатора –
ДНК-полимераза (EC 2.7.7.7), которая синтезирует ДНК в строгом соответствии последовательностью нуклеотидов в другой ДНК, которая
используется как "эталон" (или шаблон, template). ДНК-полимераза "ошибается" (вставляет "ошибочный" нуклеотид) реже, чем один раз на миллион синтезов.
Каталитическая активность многих ферментов может изменяться в
зависимости от концентрации веществ-регуляторов больше, чем от концентрации их субстратов. Возможность регулирования активности ферментов делает их своеобразными организаторами обменных процессов в
клетке.
Особенность ферментативных реакций – мягкие условия протекания: температура ~37°С, нормальное атмосферное давление; pH, близкое к
нейтральному. В противоположность этому для эффективного химического катализа часто требуются высокие температура и давление, а также
экстремальные значения pH.
9
Ферменты могут преобразовывать энергию из одной формы в другую. Фермент миозин преобразует энергию химических связей АТФ в механическую энергию мышечных сокращений.
"Насосы" в биологических мембранах, которые можно рассматривать как ферменты, которые перемещают субстрат через мембрану, а не
химически изменяют его, создают градиенты химического или электрического потенциала, используя энергию АТФ. Например, на рисунке 2 представлена Ca2+-АТФаза (EC 3.6.1.38), которая используя энергию гидролиза
АТФ на АДФ и неорганический фосфат Pi для транспорта ионов Са2+ через мембрану, создает тем самым градиент ионов Са2+.
Молекулярные механизмы подобных ферментов-преобразователей
энергии включают в себя "конвейер" элементарных стадий – связывание
иона, механическое перемещение, освобождение иона, – что сопровождается взаимным превращением различных форм энергии.
Перечисленные особенности ферментов, отличающие их от других
типов катализаторов, объясняются особенностями пространственной организации глобулярных ферментных белков. Именно взаимное расположение в пространстве различных звеньев полипептидных цепей и
кофакторов и их пространственное перемещение в ходе ферментативной
реакции объясняют особенности и многообразие ферментов.
1.3. ЭНЕРГЕТИКА БИОХИМИЧЕСКИХ РЕАКЦИЙ
Рисунок 2 – Фермент Ca2+-АТФаза преобразующий энергию, используя энергию гидролиза АТФ для транспорта ионов Са2+ через мембрану, создает градиент ионов Са2+
10
В биохимических ферментативных реакциях, так же как и в любых
других химических реакциях, часть межатомных связей в субстрате разрывается (либо модифицируется), при этом возникают новые межатомные
связи, которые и отличают продукт каталитической реакции от субстрата.
Работу, которая совершается в биохимической реакции при ферментативном превращении веществ, называют химической работой.
Условно принято различать следующие формы энергии; механическую, электрическую, химическую и энергию излучения. При этом работа
и энергия – взаимосвязанные величины. Обе величины, энергия и работа,
измеряются в джоулях (1 Дж = 1 H/м). Устаревшая внесистемная единица
– калория (1 кал = 4,187 Дж).
Свободная энергия определяется как та часть энергии системы, которая может производить работу.
Система в состоянии производить работу, когда она переходит из
начального состояния в конечное с уменьшением энергии (химического
потенциала). Это абстрактное положение наиболее наглядно демонстрируется на примере совершения механической работы (рисунок 3): благодаря силе земного притяжения энергия предмета (потенциальная
механическая энергия), в данном случае энергия воды, тем выше, чем
дальше этот предмет удален от центра Земли.
11
той "движущей силой" биохимической реакции, которая совершает химическую работу.
МеханиВысота
м
ческая
ЭлекДж
тричес- Напряжение В=
Кл
кая
Изменение
Дж
Химисвободной
ческая
моль
энергии ΔG
а
б
Дж
м
(Высота)×
×(Вес)
Дж
Заряд
Кл
(Напряжение)×(Заряд)
Дж
Количество
вещества
моль
( ΔG )×(Количество вещества)
Дж
Фактор емкости (ФЕ)
Вес (масса)
в
Рисунок 3 – Разность потенциалов в различных видах работы: а – механическая
работа, б – электрическая работа, в – химическая работа
Совершаемая работа может рассматриваться как произведение двух
величин: фактора интенсивности или разности потенциалов, т.е. "движущей силы" процесса и фактора емкости (таблица 2).
В случае совершения электрической работы (рисунок 3(б)) фактор
интенсивности – электрическое напряжение, т. е. разность электрических
потенциалов источника тока и "земли", а фактор емкости – величина заряда.
Предположим, что превращение энергии в биохимических реакциях
следует тем же закономерностям. Тогда свободная энергия есть произведение разности химических потенциалов исходных веществ и продуктов
химической реакции (фактор интенсивности) на количество вещества
(в молях) (фактор емкости). Разность химических потенциалов и является
12
Работа =
(ФИ)·(ФЕ)
Единицы
измерения
Фактор инФормы
тенсивности
работы
(ФИ)
Единицы
измерения
Таблица 2 – Факторы интенсивности и емкости в различных видах
работы
Единицы
измерения
Перепад высот между высокой и низкой точками определяется как
разность потенциалов (ΔР). Поток воды самопроизвольно устремляется
вниз, по градиенту потенциала, и при этом совершает работу, например,
вращает колесо водяной мельницы.
Возможность спонтанного прохождения какого-либо процесса зависит от того, какой знак будет иметь разность химических потенциалов конечного и исходного состояния системы (ΔΡ = P2 – Р1). Если P2 меньше Р1
и ΔΡ – величина отрицательная, то процесс идет спонтанно и при этом
производится работа. Такой процесс носит название экзергонического.
Если разность потенциалов близка к нулю, то система находится в равновесии. В случае эндергонического процесса ΔΡ – величина положительная,
т. е. процесс не может идти самопроизвольно.
Для того чтобы реализовать эндергонический процесс, необходимо
энергетически сопрячь его с энергетически более эффективным экзергоническим процессом (воспользоваться принципом энергетического сопряжения).
Наиболее наглядно это можно продемонстрировать на примере механической работы (рисунок 4): когда две массы M1 и M2 связаны шнуром, M1 будет двигаться вверх, несмотря на то, что этот процесс
13
эндергонический, т.е. в сопряженной системе определяющим фактором
будет сумма разностей потенциалов двух процессов (ΔРЭФФ = ΔP1 + ΔP2).
Суммарный процесс возможен при условии, если ΔРЭФФ – величина отрицательная.
UM
Механическая работа сил потенциального гравитационного поля
по перенесению тела массой m на высоту h имеет вид
G G
WM = ∫ F d r = mgh .
0
h
Работа WE сил потенциального электростатического поля по перенесению заряда q вдоль цепи L между точками с разностью потенциалов Δϕ имеет вид
G G
WE = ∫ F d r = qΔϕ .
L
По аналогии с работой потенциальных сил, формально можно ввести работу химических сил W X , которая совершается в химической реакции, если использовать понятие химического потенциала μ и количества
а
б
в
г
Рисунок 4 – Примеры энергетических процессов: а – экзергонический процесс;
б – равновесный процесс; в – эндергонический процесс; г – энергетически сопряженный процесс
Благодаря энергетическому сопряжению возможно взаимопревращение одних форм работы и энергии в другие.
Например, в батарейке карманного фонарика экзергоническая химическая реакция создает электрический ток, который используется для
эндергонического процесса получения световой энергии в лампочке накаливания.
В мышцах химическая энергия трансформируется в механическую
работу и тепловую энергию.
G
Формально сила F определяется как градиент потенциальной энергии U , взятый с обратным знаком
G
F = − gradU .
14
вещества ν
WX = νΔμ .
Биохимические реакции протекают в конденсированной фазе, изменение объема системы в результате реакции пренебрежимо мало и, поэтому, несущественным становится различие между энтальпией H и
внутренней энергией U системы, а, значит, и между такими термодинамическими потенциалами как энергия Гиббса G и свободная энергия
Гельмгольца A . Оба этих потенциала в биофизике и биохимии принято
называть свободной энергией и обозначать изменение свободной энергии
биохимической реакции, как ΔG .
Изменение свободной энергии ( ΔG ) химической реакции зависит от
ряда факторов, в том числе от температуры и концентрации реагентов.
Все химические реакции сопровождаются выделением или поглощением тепла. Реакции первого типа называются экзотермическими, реакции второго типа – эндотермическими.
15
Мерой теплоты реакции служит изменение энтальпии ΔH , которая
соответствует теплообмену при постоянном давлении.
В случае экзотермических реакций система теряет тепло и ΔH –
величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔH – величина положительная.
Теплота реакции ΔH и изменение свободной энергии ΔG не всегда
имеют сравнимые значения. В действительности известны реакции, протекающие спонтанно ( ΔG < 0 ) несмотря на то, что являются эндотермическими ( ΔH > 0 ). Это происходит потому, что на прохождение реакции
оказывает влияние изменение степени упорядоченности системы.
Мерой изменения упорядоченности системы служит изменение энтропии ΔS . Энтропия системы тем выше, чем больше степень неупорядоченности (беспорядка) системы.
Таким образом, если процесс идет в направлении увеличения
неупорядоченности системы (а повседневный опыт показывает, что это
наиболее вероятный процесс), ΔS – величина положительная. Для увеличения степени порядка в системе ( ΔS > 0 ) необходимо затратить энергию.
Оба этих положения вытекают из фундаментального закона природы – второго начала термодинамики. Количественно зависимость между
изменениями энтальпии, энтропии и свободной энергии описывается
уравнением Гиббса-Гельмгольца
В результате увеличения степени упорядоченности ( ΔS < 0 ) член уравнения ( − TΔS ) – величина положительная, однако это с избытком компенсируется ростом энтальпии: в итоге происходит высоко экзергоническая
реакция ( ΔG 0 ).
ΔG = ΔH − TΔS .
Поясним зависимость этих трех величин на двух примерах (рисунок 5).
Пример 1. Взрыв гремучей смеси. Взрыв гремучей смеси – это
взаимодействие двух газов – кислорода и водорода – с образованием воды
2H 2 + O 2 = 2H 2 O .
Как и многие окислительно-восстановительные реакции это сильно
экзотермический процесс (т.е. ΔH 0 ). В то же время в результате реакции возрастает степень упорядоченности системы. Газ с его хаотически
мигрирующими молекулами перешел в более упорядоченное состояние –
жидкую фазу, при этом число молекул в системе уменьшилось на 1/3.
16
а
б
Рисунок 5 – Энтальпийный и энтропийный процессы: а – взрыв гремучей смеси; б – растворение NaCl в воде
17
Пример 2. Растворение в воде поваренной соли. При растворении
в воде поваренной соли ΔH > 0 – величина положительная, температура в
сосуде с раствором, т. е. в объеме раствора, снижается. Тем не менее, процесс идет спонтанно, поскольку степень упорядоченности системы
уменьшается. В исходном состоянии ионы Na+ и Cl– занимали фиксированные положения в кристаллической решетке. В растворе они перемещаются независимо друг от друга в произвольных направлениях.
Снижение упорядоченности ( ΔS > 0 ) означает, что член уравнения
( −T ΔS ) имеет знак минус. Это компенсирует ΔH и в целом ΔG – величина отрицательная. Такие процессы принято называть энтропийными.
Для стимуляции энергозатратных эндергонических процессов в
биосистемах используется энергия других высокоэнергетичных процессов, а именно:
1) разрыв химических связей,
2) поглощение света,
3) рекомбинация предварительно разделенных зарядов.
В биосистемах можно найти множество примеров использования
всех трех "источников" дополнительной энергии – энергии химических
связей, энергии света и электрической энергии.
Эти дополнительные "источники" используются главным образом
двумя способами:
1) чтобы активировать химические реакции,
2) для стимуляции механического движения.
Живые клетки не пользуются теми способами утилизации энергии,
которые использует человек. Человек обычно аккумулирует большое количество энергии, а затем использует этот запас. Примером такого подхода является двигатель автомобиля, в котором взрывное сгорание бензина
является источником механического движения. Клетки не используют
реакции, в которых выделяется много энергии, поскольку термическая
энергия быстро рассеивается, и наносистема не успевает её использовать.
18
При этом, однако, следует помнить, что при необходимости тепло в
большом количестве может продуцироваться живыми организмами,
причем на уровне всего организма. Значительное тепловыделение происходит либо в результате механического трения при работе клеток мускулатуры, либо вследствие химических экзотермических реакций при
интенсификации гидролиза молекул жиров.
Но на клеточном уровне энергия выделяется небольшими порциями
так, чтобы она могла быть контролируемо и эффективно использована.
Природные бионаномашины используют энергетическое сопряжение процессов. Так две химические реакции могут быть сопряжены, и экзергоническая реакция будет стимулировать эндергоническую.
Например, фермент пируват-киназа сопрягает реакции отщепления
фосфат-группы от фосфоэнолпирувата (экзергоническая реакция) и присоединения этой фосфат-группы к АДФ (эндергоническая реакция). Вторая реакция не происходит спонтанно, но, будучи сопряженной с первой,
весь процесс может протекать самопроизвольно.
Аналогично химические реакции зачастую сопрягаются с электрическими процессами, или же поглощение света используется для стимуляции химических реакций, или могут быть использованы другие
комбинации процессов. Ключевым моментом здесь является внутримолекулярный или межмолекулярный перенос энергии на нанорасстояния.
1.4. ОСНОВНЫЕ ПОНЯТИЯ ХИМИЧЕСКОГО КАТАЛИЗА
Катализом называется явление изменения скорости химической реакции в присутствии катализаторов.
Катализ называется положительным, если скорость реакции увеличивается, и отрицательным, если скорость уменьшается.
Катализ называется гомогенным, если реагенты и катализатор находятся в одной фазе, и гетерогенным, если – в разных фазах.
Катализатором называется вещество, которое участвует в химической реакции и изменяет её скорость, но не входит в состав конечных продуктов и остается неизменным после завершения химической реакции.
Катализатор, замедляющий реакцию, называется ингибитором.
19
Как уже говорилось выше, биологические катализаторы белковой
природы называют ферментами.
Поскольку катализатор не входит в состав как исходных веществ,
так и продуктов реакции, то он не может оказать влияние на изменение
энергии Гиббса ΔG . Следовательно, он не может вызвать протекание
реакций, для которых в данных условиях ΔG > 0 , а может лишь ускорить
скорость реакции в том случае, если ΔG < 0 (рисунок 6).
В состоянии равновесия (ΔG = 0) катализатор в равной степени ус-
Энергия
коряет как прямую, так и обратную реакции.
A = wK − w0 .
Часто скорость реакции без катализатора, w0 , настолько мала, что
вторым слагаемым пренебрегают:
A = wK .
Если реакция протекает вблизи состояния равновесия и является
двухсторонней, то за меру каталитической активности принимают скорость протекания реакции в прямом направлении.
Е'а Eа
ΔG
Реагенты
Продукты
Координата реакции
Рисунок 6 – Влияние катализатора на величину энергетического барьера
Механизм действия катализаторов связан с тем, что они образуют
промежуточные соединения с исходными веществами и тем самым изменяют путь реакции, причем новый путь характеризуется меньшей высотой энергетического барьера, т.е. меньшими энергиями активации Ea1, Ea 2
по сравнению с E a в исходной (некатализируемой) реакции (рисунок 7).
Поэтому встречающееся зачастую утверждение о том, что катализатор снижает энергию активации, не корректно, так как реакция в присутствии катализатора не идентична исходной реакции. Просто это
совершенно иная реакция, имеющая более низкий активационный барьер.
Каталитическая активность A характеризует изменение скорости
данной реакции, w , при введении в реакционную систему катализатора
20
а
б
Рисунок 7 – Влияние катализатора на энергетический профиль реакции:
а – энергетический профиль в отсутствие катализатора; б – энергетический профиль в
присутствии катализатора
Удельной каталитической активностью называется каталитическая активность, отнесенная к единице массы катализатора.
Селективностью (избирательностью) катализатора называется его
способность ускорять один из возможных путей реакции, если она может
протекать по разным направлениям с образованием различных продуктов.
Промежуточное химическое взаимодействие реагентов с катализатором может протекать слитно (рисунок 8(а)) или раздельно (рисунок 8(б)).
При слитном каталитическом процессе в состав активированного
комплекса входят катализатор и все реагирующие вещества.
21
Так элементарная реакция
В каждой последовательной стадии рвется только часть старых связей, поэтому энергии активации таких разрывов E2′ и E2′′ заметно меньше
A+B→D+E
энергии активации некатализируемой реакции E1 .
без катализатора протекает через активированный комплекс AB≠
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
≠
A + B → AB → D + E ,
а в присутствии катализатора – через активированный комплекс ABK ≠
A + B + K → ABK ≠ → D + E + K .
E
E
E1
E1
1
2
E2′
1
E2′′
E2
2
А+В+К
A+B+K
D+E+K
Координата реакции
AK + B
а
D+E+K
б
Рисунок 8 – Энергетический профиль реакции: а – при слитном каталитическом
процессе; б – при раздельном каталитическом процессе
Увеличение скорости при слитном механизме достигается в результате уменьшения энергии активации. При раздельном механизме каталитический процесс осуществляется поэтапно, в виде нескольких стадий.
Энергетический профиль реакционного пути характеризуется при
этом несколькими максимумами (активированные комплексы отдельных
стадий) и минимумами (продукты промежуточного взаимодействия).
Например, для случая, приведенного на рисунке 8(б),
A + K → AK ≠ → AK ,
AK + B → AKB≠ → D + E + K .
22
1. Что изучает энзимология?
2. Что такое ферменты?
3. Какова роль ферментов в клеточном метаболизме?
4. Что такое рибозимы?
5. Что такое субстрат?
6. Что называется апоферментом?
7. Что называется кофактором?
8. Что называется холоферментом?
9. В чём сходство и различие апофермента и кофактора?
10. В чём сходство и различие апофермента и холофермента?
11. В чём сходство и различие кофактора и холофермента?
12. Какие виды кофакторов вы знаете?
13. Что называется коферментом?
14. Что называется простетической группой?
15. Может ли апофермент быть простетической группой? Почему?
16. В чём отличие биокатализаторов от небиологических катализаторов?
17. Чем активность ферментов отличается от активности небиологических катализаторов?
18. В каких единицах измеряется активность фермента?
19. Что называется числом оборотов ферментативной реакции?
20. Что называется удельной активностью ферментативной реакции?
21. Что называется молярной активностью ферментативной реакции?
22. Сколько международных единиц ферментативной активности составляет один катал?
23. Что называется специфичностью действия фермента?
24. Что такое субстратная специфичность ферментов?
23
25. Чем специфичность ферментов отличается от специфичности небиологических катализаторов?
26. Что такое специфичность пути превращения ферментов?
27. Почему способность к регуляции отличает ферменты от небиологических катализаторов?
28. В каком температурном диапазоне работает большинство ферментов? Сравните с условиями работы небиологических катализаторов.
29. При каких значениях рН работает большинство ферментов?
Сравните с условиями работы небиологических катализаторов.
30. При каком значении атмосферного давления работает большинство ферментов? Сравните с условиями работы небиологических
катализаторов.
31. Приведите примеры преобразования ферментами энергии из одной формы в другую.
32. Какие процессы называются эндергоническими? Приведите пример биологического эндергонического процесса.
33. Какие процессы называются экзергоническими? Приведите пример биологического экзергонического процесса.
34. В чём заключается принцип энергетического сопряжения? Приведите примеры энергетически сопряженных биологических процессов.
35. Как изменение свободной энергии в ходе биологического процесса характеризует самопроизвольность этого процесса?
36. Запишите уравнение Гиббса-Гельмгольца. Какие вклады в свободную энергию учитывает это уравнение?
37. Какие процессы называются энтропийными? Приведите примеры.
38. В чём сходство и различие гомогенного и гетерогенного каталитических процессов?
39. Как изменяется путь реакции при наличии в системе катализатора?
40. В чём сходство и различие слитного и раздельного каталитических процессов?
24
Глава 2
КЛАССИФИКАЦИЯ ФЕРМЕНТОВ
2.1. ОСНОВЫ КЛАССИФИКАЦИИ ФЕРМЕНТОВ
На сегодняшний день известно более 10000 ферментов. Динамика
нарастания количества обнаруживаемых в природе ферментов представлена в таблице 3, а их классификация – в таблице 4.
И хотя в настоящее время считается, что известны все основные
ферменты, катализирующие химические реакции основных метаболических процессов в клетке, однако новые ферменты открывают регулярно.
Таблица 3 – Динамика нарастания количества обнаруженных в природе ферментов
Год 1930
Число ферментов
80
1947
1957
1962
1972
1975
1994
200
660
880
1770
2140
3200
Исторически многие ферменты имеют названия, которые ничего не
говорят о катализируемой реакции. Пример: рассмотренные выше ферменты трипсин и каталаза.
Большинство ферментов, напротив, названы по катализируемым реакциям и субстратам. Например, фермент, разрушающий АТФ, называется АТФаза, а фермент, синтезирующий АТФ – АТФ-синтетаза.
В этих случаях название фермента складывается либо из названия
субстрата с прибавлением суффикса -аза , либо суффикс добавляется к
названию катализируемой реакции.
Например, аргиназа катализирует гидролиз аргинина, фосфатаза
гидролизует фосфорные эфиры; дегидрогеназа катализирует отрыв водорода, гидролаза катализирует гидролиз, трансфераза переносит химические группы и т.д.
Для унификации номенклатуры ферментов разработана система
классификации с учетом реакционной и субстратной специфичности фер25
ментов. Все ферменты включены в Каталог ферментов (Enzyme Catalog,
EC) Номенклатурного Комитета Международного Общества Биохимии и
молекулярной Биологии (International Union of Biochemistry and Molecular
Biology) http://www.chem.qmul.ac.uk/iubmb/enzyme/ под своим классификационным номером, состоящим из четырех цифр.
Таблица 4 – Классы ферментов
№
Класс
Тип реакции
1 Оксидоредуктазы
2 Трансферазы
Важнейшие подклассы
Дегидрогеназы
Оксидазы
Пероксидазы
Редуктазы
Монооксигеназы
Диоксигеназы
С1-Трансферазы
Гликозилтрансферазы
Аминотрансферазы
Фосфотрансферазы
3 Гидролазы
Эстеразы
Гликозидазы
Пептидазы
Амидазы
Лиазы
4 ("синтазы")
С-С Лиазы
С-О Лиазы
С-N Лиазы
С-S Лиазы
5 Изомеразы
Эпимеразы
цис-трансизомеразы
Внутримолекулярные трансферазы
Лигазы
6 ("синтетазы")
С-С Лигазы
С-О Лигазы
С-N Лигазы
С-S Лигазы
26
Первая цифра указывает на принадлежность к одному из шести
главных классов. Следующие две определяют подкласс и подподкласс, а
последняя цифра – номер фермента в данном подподклассе. Например,
лактатдегидрогеназа имеет номер EC 1.1.1.27 (класс 1, оксидоредуктазы;
подкласс 1.1, донор электрона – группа СН–ОН; подподкласс 1.1.1, акцептор электрона – НАДФ+ (NADP+)).
В каждом из шести главных классов объединены ферменты, обладающие одинаковой реакционной специфичностью (таблица 4).
Оксидоредуктазы (класс 1) катализируют окислительно-восстановительные реакции.
Трансферазы (класс 2) переносят ту или иную функциональную
группу от одного субстрата на другой. Для оксидоредуктаз и трансфераз
необходим общий кофермент.
Гидролазы (класс 3) также участвуют в переносе групп, однако акцептором здесь всегда является молекула воды.
Лиазы (класс 4, называемые иногда "синтазами") катализируют расщепление или образование химических соединений, при этом образуются
или исчезают двойные связи.
Изомеразы (класс 5) перемещают группы в пределах молекулы без
изменения общей формулы субстрата.
Лигазы ("синтетазы", класс 6) катализируют энергозависимые реакции присоединения и поэтому их действие сопряжено с гидролизом нуклеозидтрифосфата (чаще всего АТФ).
2.2. ОКСИДОРЕДУКТАЗЫ
Существует несколько типов окислительно-восстановительных
ферментативных реакций. Ферменты класса 1 оксидоредуктазы переносят водород (протоны) или электроны и катализируют биологическое
окисление. В состав оксидоредуктаз входят специфические коферменты.
Оксидоредуктазы подразделяются на подклассы в соответствии с
донором, от которого переносится водород или электрон (подклассы обозначаются 1.n).
27
1.1. Оксидоредуктазы подкласса 1.1 действуют на СН–ОН группы в
молекулах доноров. Подподклассы определяются в соответствии с
акцептором, к которому идет перенос (подподклассы обозначаются 1.n.n).
1.1.1. Акцептором у оксидоредуктаз подподкласса 1.1.1 служит
НАД+ (никотинамид-аденин-динуклеотид, NAD+) или НАДФ+ (никотинамид-аденин-динуклеотид-фосфат, NADP+) (см. п. 6.3). Общее название
ферментов данного подподкласса – дегидрогеназы или редуктазы.
Например, фермент алкогольдегидрогеназа (EC 1.1.1.1) катализирует реакцию превращения этанола (спирта) в этаналь (ацетальдегид).
Фермент гидроксиметилглутарил-СоА-редуктаза (EC 1.1.1.34) в
метаболизме
холестерина
катализирует
реакцию
превращения
3-гидрокси-3-метил-глутарил-СоА в мевалонат.
1.2. Оксидоредуктазы подкласса 1.2 действуют на альдегидную или
кетонную группы в молекулах доноров.
1.2.1. Акцептором служит НАД+ или НАДФ+. Общее название ферментов данного подподкласса – дегидрогеназы.
Например, фермент альдегиддегидрогеназа (EC 1.2.1.3) в метаболизме этанола превращает этаналь в ацетат.
1.1.2. Акцептором служит цитохром.
1.1.3. Акцептором служит молекулярный кислород. Общее название
ферментов данного подподкласса – оксидазы. Оксидазы обычно присоединяют водород или электрон (из субстрата) к кислороду с образованием
пероксида водорода H2O2.
Например, фермент ксантиноксидаза (EC 1.1.3.22) в метаболизме
нуклеотидов превращает ксантин (2,6-диоксипурин) в мочевую кислоту
(2,6,8-триоксипурин).
Еще пример фермента этого подподкласса – глицеральдегид-3фосфатдегидрогеназа (ЕС 1.2.1.12) (см. стр. 186).
1.2.3. Акцептором служит молекулярный кислород.
1.2.4. Акцептором служит дисульфидная группа.
1.3. Оксидоредуктазы подкласса 1.3 действуют на –СН–СН– группы
в молекулах доноров.
1.4. Оксидоредуктазы подкласса 1.4 действуют на –СН–NН2 группы
в молекулах доноров.
1.5. Оксидоредуктазы подкласса 1.5 действуют на –СН–NН группы
в молекулах доноров.
1.6. Оксидоредуктазы подкласса 1.6 используют в качестве донора
НАДФН.
Например, компонентом комплекса I дыхательной цепи на внутренней митохондриальной мембране является фермент НАДФ-дегидрогеназа
(EC 1.6.5.3), который окисляет дигидропиридины в пиридины, образо-
28
29
вавшиеся электроны переносятся на убихиноны (коферменты Q), а протоны накапливаются в межмембранном пространстве митохондрии, образуя
трансмембранный протонный градиент.
1.11. Оксидоредуктазы подкласса 1.11 используют в качестве акцептора пероксид водорода H2O2.
Общее название ферментов данного подкласса – пероксидазы.
Обобщенно схему реакций, в которых окислителем является перекись водорода, можно записать в виде
Субстрат + Н2О2 → Окисленный субстрат + 2Н2О.
1.7. Оксидоредуктазы подкласса 1.7 используют в качестве доноров
другие азотистые соединения группы.
1.8. Оксидоредуктазы подкласса 1.8 используют в качестве доноров
серосодержащие группы.
1.9. Оксидоредуктазы подкласса 1.9 используют в качестве донора
группу гема.
Например, фермент цитохром-с-оксидаза (EC 1.9.3.1), входящий в
состав комплекса IV дыхательной цепи внутренней митохондриальной
мембраны, на котором перенос электрона с гемсодержащего белка цитохрома с на молекулярный кислород сопряжен с переносом протонов через
мембрану и созданием протонного градиента, окисляет ферропорфирин в
феррипорфирин.
1.10. Оксидоредуктазы подкласса 1.10 используют в качестве донора дифенол.
30
Например, гем-содержащий фермент каталаза (EC 1.11.1.6) катализирует превращение перекиси водорода в воду и кислород
2Н2О2 → О2 + 2Н2О.
1.13. Оксидоредуктазы подкласса 1.13 включают в окисляемый субстрат (донор электронов) молекулярный кислород. Общее название ферментов данного подкласса – оксигеназы.
1.14. Оксидоредуктазы подкласса 1.14 включают в два окисляемых
субстрата (доноры электронов) один атом кислорода.
Общее название ферментов данного подкласса – монооксигеназы,
гидроксилазы.
Например, фермент триптофан-5-монооксигеназа катализирует
присоединение гидроксильной группы к триптофану в положении 5.
1.15. Оксидоредуктазы подкласса 1.15 используют в качестве акцептора супероксид-радикал.
1.17. Оксидоредуктазы подкласса 1.17 используют в качестве донора –СН2-группу.
1.18. Оксидоредуктазы подкласса 1.18 используют в качестве донора восстановленный ферредоксин. Например, фермент нитрогеназа
31
(ЕС 1.18.6.1) катализирует разрыв молекулярных связей в молекуле азота
в азотфиксирующих бактериях и сине-зеленых водорослях.
2.3. ТРАНСФЕРАЗЫ
Трансферазы переносят группы атомов с помощью специфических
переносчиков, которые действуют как коферменты. Трансферазы участвуют в биохимических превращениях и могут переносить метильные, карбоксильные, амино-, сульфо-, формильные (С1) или фосфорильные
группы.
2.1. Трансферазы подкласса 2.1 переносят одноуглеродные группы
(С1-фрагменты).
2.1.1. Метилтрансферазы.
2.1.2. Трансферазы оксиметильных, формильных и родственных им
групп.
2.1.3. Карбоксилтрансферазы и карбомилтрансферазы.
2.2. Трансферазы подкласса 2.2 переносят альдегидные и кетонные
группы.
2.3. Ацилтрансферазы.
тидной цепи от тРНК, находящейся в Р-центре на аминогруппу, присоединенную к тРНК, находящейся в А-центре рибосомы.
2.4. Гликозилтрансферазы.
2.4.1. Трансферазы подподкласса 2.4.1 переносят остаток гексозы –
гексозилтрансферазы.
Например, фермент фосфорилаза (или гликогенфосфорилаза)
(EC 2.4.1.1) катализирует расщепление связи в субстрате с одновременным присоединением фосфатной группы к продукту реакции
(глюкоза)n + HPO42– → (глюкоза)n–1 + глюкоза-1-фосфат.
2.4.2. Трансферазы подподкласса 2.4.2 переносят остатки пентозы –
пентозилтрансферазы.
2.5. Трансферазы подкласса 2.5 переносят алкильные или арильные
группы.
2.6. Трансферазы подкласса 2.6 переносят азотсодержащие группы.
2.6.1. Аминотрансферазы или трансаминазы.
Например, фермент аспартаттрансаминаза (EC 2.6.1.1) переносит
аминогруппу с аспартата на 2-оксоглутарат с образованием глутамата.
2.3.1. Донором служит СоА.
Например, фермент ацетил-СоА-С-ацилтрансфераза (EC 2.3.1.16)
при высоких концентрациях молекул ацетил-СоА катализирует реакцию
присоединения ещё одной ацильной группы к ацетилу-СоА с образованием молекулы ацетоацетил-СоА.
2.3.2. Аминоацилтрансферазы. Например, фермент рибосомная
пептидилтрансфераза (EC 2.3.2.12) катализирует перенос растущей пеп32
2.6.2. Амидинотрансферазы.
2.6.3. Оксиминотрансферазы.
2.7. Трансферазы подкласса 2.7 переносят фосфоросодержащие
группы. Общее название ферментов данного подкласса – киназы или
фосфотрансферазы.
33
2.7.1. Акцептором служит спиртовая группа –СН–ОН. Ферментами
данного подподкласса являются, например, 6-фосфофруктокиназа (ЕС
2.7.1.11) (см. п. 8.5), протеинкиназа (EC 2.7.1.37), киназа фосфорилазы
(EC 2.7.1.38) и пируваткиназа (ЕС 2.7.1.40) (см. п. 8.5). Фермент глюкокиназа (или гексокиназа (ЕС 2.7.1.1)) переносит фосфатную группу от АТФ
на глюкозу, образуя молекулу глюкоза-6-фосфат.
2.7.2. Фосфотрансферазы, с карбоксильной группой (–СООН) в роли акцептора. Например, ферменты фосфоглицераткиназа (EC 2.7.2.3)
(см. п. 8.5), аспартаткиназа (EC 2.7.2.4) и ацетилглутаматкиназа
(EC 2.7.2.8).
2.7.3. Фосфотрансферазы, с азотсодержащими группами в роли акцептора, например, фермент креатинкиназа (EC 2.7.3.2).
2.7.4. Фосфотрансферазы, с фосфатной группой в роли акцептора.
Например, ферменты аденилаткиназа (EC 2.7.4.3) и нуклеозидфосфаткиназа (EC 2.7.4.4).
2.7.5. Фосфотрансферазы, катализирующие реакции кажущегося
внутримолекулярного переноса.
2.7.6. Фосфотрансферазы, катализирующие реакции переноса дифосфатных остатков.
Общее название ферментов данного подподкласса – пирофосфаттрансферазы.
2.7.7. Фосфотрансферазы, катализирующие реакции переноса нуклеотидов. Общее название ферментов данного подподкласса – нуклеотидилтрансферазы.
34
Например, ферменты ДНК-зависимая РНК-полимераза (РНК-полимераза) (EC 2.7.7.6), ДНК-зависимая ДНК-полимераза (ДНК-полимераза)
(EC 2.7.7.7), РНК-зависимая ДНК-полимераза (обратная транскриптаза
или ревертаза) (EC 2.7.7.49).
2.7.8. Фосфотрансферазы, катализирующие реакции переноса других замещенных фосфатных групп.
Например, этаноламинфосфотрансфераза (EC 2.7.8.1), 1-алкил-2ацетилглицерин-холинфосфотрансфераза (EC 2.7.8.16).
2.8. Трансферазы подкласса 2.8 переносят группы, содержащие серу.
2.8.1. Сульфидтрансферазы.
2.8.2. Сульфотрансферазы переносят группу –SO3H.
2.4. ГИДРОЛАЗЫ
Гидролазы катализируют гидролитическое расщепление и называются в соответствии с типом разрываемой связи.
3.1. Гидролазы подкласса 3.1 гидролизуют сложноэфирные связи.
Общее название ферментов данного подкласса – эстеразы.
3.1.1. Гидролазы эфиров карбоновых кислот. Например, фермент
триацилглицерин-липаза (EC 3.1.1.3) гидролизует триацилглицеролы.
35
Фермент ацетилхолинэстераза (EC 3.1.1.7) гидролизует ацетилхолин на холин и уксусную кислоту.
3.1.5. Гидролазы трифосфомоноэфиров.
3.1.6. Гидролазы сульфоэфиров.
3.1.21. Гидролазы ДНК. Например, ферменты дезоксирибонуклеаза I
(EC 3.1.21.1), специфическая дезоксирибонуклеаза (тип II) (эндонуклеаза
рестрикции или рестриктаза) (EC 3.1.21.4).
3.1.26–27. Гидролазы РНК.
3.2. Гидролазы подкласса 3.2 гидролизуют гликозидные связи. Общее название ферментов данного подкласса – гликозидазы.
Например, фермент α-гликозидаза (мальтоза) гидролизует молекулу мальтозы на две молекулы α-D-глюкозы
3.1.2. Гидролазы тиоловых эфиров.
3.1.3. Гидролазы фосфомоноэфиров. Общее название ферментов
данного подподкласса – фосфатазы.
Например, фермент щелочная фосфатаза (EC 3.1.3.1) катализирует
реакцию
3.1.4. Гидролазы фосфодиэфиров.
Общее название ферментов данного подподкласса – фосфодиэстеразы. Они гидролизуют фосфодиэфирную связь.
36
3.2.1. Гидролазы гликозидов. Например, α-амилаза (EC 3.2.1.1) и
лизоцим (3.2.1.17).
3.2.2. Гидролазы N-гликозильных соединений.
3.2.3. Гидролазы S-гликозильных соединений.
3.3. Гидролазы подкласса 3.3 гидролизуют простые эфирные связи.
3.4. Гидролазы подкласса 3.4 гидролизуют пептидные связи.
Общее название ферментов данного подкласса – пептидазы.
Некоторые из 99 подподклассов пептидаз.
3.4.11. Аминопептидазы (N-концевые экзопептидазы).
3.4.13. Дипептидазы (действуют только на дипептиды).
3.4.15. Пептидилдипептидазы (С-концевые экзопептидазы, освобождающие дипептид).
37
3.4.17. Карбоксипептидазы (С-концевые экзопептидазы).
3.4.21. Сериновые протеазы (эндопептидазы).
Например, ферменты химотрипсин (EC 3.4.21.1), трипсин (EC
3.4.21.4), тромбин (EC 3.4.21.5), различные факторы свертывания крови.
3.4.22. Цистеиновые протеиназы (эндопептидазы). Например, фермент папаин (EC 3.4.22.1).
3.4.23. Аспартатные протеиназы (эндопептидазы). Например, фермент пепсин А (EC 3.4.23.1), ренин (EC 3.4.23.15).
3.4.24. Металлопротеиназы (эндопептидазы). Например, фермент
коллагеназа (EC 3.4.24.7).
3.4.99. Другие пептидазы. Например, фермент сигнальная пептидаза (EC 3.4.99.36).
3.5. Гидролазы подкласса 3.5 гидролизуют C–N связи, отличные от
пептидных связей. Общее название ферментов данного подкласса – амидазы.
3.6. Гидролазы подкласса 3.6 гидролизуют ангидридные связи.
Например, ферменты
− нуклеозид-дифосфотаза (EC 3.6.1.6),
− миозин-АТФаза (EC 3.6.1.32),
− Н+-транспортирующая АТФ-синтаза (АТФ-синтаза,
комплекс V) (EC 3.6.1.34),
2.5. ЛИАЗЫ
Лиазы разрывают или образуют связи без участия окисления или
гидролиза.
4.1. Лиазы подкласса 4.1 образуют или расщепляют С–С связи. Общее название ферментов данного подкласса – углерод-углерод лиазы.
4.1.1. Карбокси-лиазы (карбоксилазы и декарбоксилазы).
Ферменты декарбоксилазы катализируют удаление СО2.
Например, фермент гидрокситриптофан декарбоксилаза катализирует образование серотонина из гидрокситриптофана.
4.1.2. Альдегид-лиазы – образуют альдегиды.
Например, фермент (EC 4.1.2.13) фруктозо-1,6-бисфосфат-альдолаза катализирует распад фруктозо-1,6-бисфосфата на глицеральдегид-3фосфат и дигидроксиацетон-3-фосфат (см. п. 8.5).
− Na+-K+-обменивающая АТФаза (Na+-K+-АТФаза)
(EC 3.6.1.37),
− Са2+-транспортирующая АТФаза (Са2+-АТФаза)
(EC 3.6.1.38).
3.7. Гидролазы подкласса 3.7 гидролизуют С–С связи. Например,
фумарилацетоацетаза (3.7.1.2).
3.8. Гидролазы подкласса 3.8 гидролизуют связи с участием галогенов.
3.8.1. В соединениях со связью углерод-галоген.
3.8.2. В соединениях со связью фосфор-галоген.
3.9. Гидролазы подкласса 3.9 гидролизуют Р–N связи.
4.1.3. Лигазы кетокислот образуют кетоны.
Например, фермент цитрат синтаза (EC 4.1.3.7) катализирует реакцию синтеза цитрата из оксалоацетата и ацетил-СоА без участия АТФ.
38
39
4.2. Лиазы подкласса 4.2 образуют или расщепляют С–О связи.
Общее название ферментов данного подкласса – углерод-кислород
лиазы.
4.2.1. Гидролиазы (гидратазы и дегидратазы).
Гидратазы – ферменты, катализирующие присоединение воды по
месту двойной связи.
Например, фермент фумарат гидратаза (фумараза) (EC 4.2.1.2) катализирует превращение фумарата в малат.
Дегидратазы – ферменты, катализирующие образование двойных
связей с образованием воды.
Например, фермент карбонат-дегидратаза (EC 4.2.1.1) (карбоангидраза) катализирует реакцию образования и разложения угольной кислоты.
лизирует реакцию дегидратации (отщепления молекулы воды) в которой
преобразуется фосфоглицерат в фосфоенолпируват (см. п. 8.5).
4.3. Лиазы подкласса 4.3 образуют или расщепляют С–N связи. Общее название ферментов данного подкласса – углерод-азот лиазы.
4.3.1. Аммиак-лиазы.
4.3.2. Амидин-лиазы.
Например, фермент аргиносукцинат-лиаза (EC 4.3.2.1) катализирует
превращение аргиносукцината в аргинин и фумарат.
4.4. Лиазы подкласса 4.4 образуют или расщепляют С–S связи.
4.5. Лиазы подкласса 4.5 образуют или расщепляют связи между углеродом и галогеном.
4.6. Лиазы подкласса 4.6 образуют или расщепляют С–Р связи.
Например, фермент аденилатциклаза (EC 4.6.1.1)
Фермент фосфопируватгидратаза или енолаза (ЕС 4.2.1.11) ката40
41
катализирует реакцию образования циклического аденозинмонофосфата
(цАМФ) из молекулы АТФ.
2.6. ИЗОМЕРАЗЫ
Изомеразы катализируют превращения изомеров, включая рацемизацию, цис-транс-изомеризацию, перемещение двойных связей, обмен
групп у асимметрического атома углерода, перемещение фосфатной группы к другому атому углерода и т. п.
5.3. Изомеразы подкласса 5.3 переносят электроны внутри молекулы – внутримолекулярные оксидоредуктазы.
Например, фермент триозофосфатизомераза (ЕС 5.3.1.1) катализирует реакцию взаимопревращения глицеральдегид-3-фосфата и дигидроксиацетонфосфата (см. п. 6.3), а фермент глюкозо-6-фосфатизомераза
(фосфоглюкоизомераза) (EC 5.3.1.9) катализирует взаимопревращение
глюкозо-6-фосфата и фруктозо-6-фосфата (см. п. 8.5).
5.1. Изомеразы подкласса 5.1 катализируют рацемизацию (рацемазы) или взаимопревращение эпимеров (эпимеразы).
Например, фермент рибулозофосфат-эпимераза (EC 5.1.3.1) катализирует взаимопревращение рибулозо-фосфата и ксилулозо-фосфата.
5.4. Изомеразы подкласса 5.4 переносят группы внутри молекулы –
внутримолекулярные трансферазы.
Общее название ферментов данного подкласса – мутазы.
Например, фермент фосфоглицератмутаза (EC 5.4.2.1) преобразует
3-фосфоглицерат в 2-фосфоглицерат перенося фосфатную группу внутри
молекулы глицерата (см. п. 8.5).
5.2. Изомеразы подкласса 5.2 катализируют цис-транс-изомеризацию. Общее название ферментов данного подкласса – цис-трансизомеразы.
Например, фермент ретинальизомераза (EC 5.2.1.3) катализирует
изомеризацию полностью транс-ретиналя в 11-цис-ретиналь.
5.5. Внутримолекулярные лиазы.
5.99. Прочие изомеразы. В частности, к этому подклассу относятся
ДНК-топоизомераза (ДНК-геликаза) (EC 5.99.1.2) и ДНК-топоизомераза
АТФ-гидролизующая (ДНК-гираза) (EC 5.99.1.3).
42
43
2.7. ЛИГАЗЫ
Лигазы являются ферментами, синтезирующими связи с помощью
макроэнергетических фосфоангидридных соединений. В качестве таких
компонентов может выступать АТФ или другое макроэнергетическое соединение, а также биотин в процессах ферментативного карбоксилирования.
6.1. Лигазы подкласса 6.1 образуют связи С–О. Например, ферменты (аминокислота)-тРНК-лигазы (аминоацил-тРНК-синтетазы)
(EC 6.1.1.n) присоединяют аминокислоту к соответствующей тРНК.
6.2. Лигазы подкласса 6.2 образуют связи С–S.
Например, фермент ацетил-СоА-лигаза (EC 6.2.1.1) катализирует
образование ацетил-СоА из ацетата и кофермента А.
6.3. Лигазы подкласса 6.3 образуют связи С–N.
Например, фермент глутамат-NH3-лигаза (глутаматсинтетаза)
(EC 6.3.1.2) катализирует образование глутамина из глутаминовой кислоты и аммиака.
6.4. Лигазы подкласса 6.4 образуют связи С–С.
Например, фермент пируват карбоксилаза (EC 6.4.1.1) катализирует
присоединение СО2 к пирувату, образуя оксалоацетат.
44
6.5. Лигазы подкласса 6.5 образуют связи Р–О. Например, фермент
ДНК-лигаза (EC 6.5.1.1).
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какие классы ферментов вы знаете?
2. Какие реакции катализируют оксидоредуктазы?
3. Как называются ферменты, которые катализируют окислительновосстановительные реакции? Приведите примеры.
4. Какие реакции катализируют трансферазы? Приведите примеры.
5. Как называются ферменты, которые катализируют перенос функциональной группы с одного субстрата на другой? Приведите
примеры.
6. Какие реакции катализируют гидролазы? Приведите примеры.
7. Как называются ферменты, которые катализируют гидролитические реакции? Приведите примеры.
8. Какие реакции катализируют лиазы? Приведите примеры.
9. Как называются ферменты, которые катализируют реакции расщепления или образования двойных связей? Приведите примеры.
10. Какие реакции катализируют изомеразы? Приведите примеры.
11. Как называются ферменты, которые катализируют реакции перенесения функциональных групп в пределах молекулы? Приведите
примеры.
12. Какие реакции катализируют лигазы? Приведите примеры.
13. Как называются ферменты, которые катализируют реакции присоединения, сопряженные с гидролизом нуклеозидтрифосфатов?
Приведите примеры.
45
цвиттер-ионы (диполярные ионы). В водном растворе аминокислоты находятся в виде цвиттер-ионов (рисунок 10(б)).
Глава 3
СТРОЕНИЕ АМИНОКИСЛОТ
COOH
COOH
3.1. КЛАССИФИКАЦИЯ АМИНОКИСЛОТ
H2N
Белки – это нерегулярные полимеры, мономерами которых являются α-L-аминокислоты.
Каждая аминокислота имеет аминогруппу, связанную с атомом углерода, с этим же атомом связана карбоксильная группа, водород и аминокислотный остаток. Такая конфигурация присутствует во всех
аминокислотах. Аминогруппа может быть присоединена к первому за
карбоксильной группой атому углерода или ко второму атому и т. д. (рисунок 9).
Атомы нумеруются греческими буквами, и в зависимости от того, к
какому по порядку атому присоединена аминокислота, её называют альфа-аминокислота, или бета-аминокислота и т. д. В состав белков входят
только альфа-аминокислоты.
а
H2N
H
R
R
H
CH
–
COO
+
NH3
R
а
б
Рисунок 10 – Структура аминокислот: а – L-конфигурация α-аминокислот;
б – схема цвиттер-иона
Существенно, что молекулы аминокислот могут отличаться своей
пространственной конфигурацией. Это явление называется стереизомерией. Такие молекулы называются D-изомерами и L-изомерами (правовращающими и левовращающими, соответственно) (рисунок 11).
D- и L-изомеры являются зеркальным отображением друг друга, и
иначе, чем через четвертое измерение они одна в другую перейти не могут. На схематических рисунках (например, на рисунке 10(а)) тот атом,
который находится ближе, перед плоскостью рисунка, принято изображать треугольной стрелкой, тот, что дальше, за плоскостью – пунктиром.
б
Рисунок 9 – Строение аминокислот: а – α-аминокислота; б – γ-аминокислота
Карбоксильная группа имеет кислотный характер, она диссоциирует
на ионы в водном растворе с образованием протона и отрицательно заряженной группы СОО¯, а аминогруппа (NH2) имеет основной характер, она
способна присоединять протон водорода, становясь положительно заряженной. В молекуле аминокислоты протон от карбоксильной группы может переносится на аминогруппу – такие образования называются
46
а
б
Рисунок 11 – Изомеры аминокислот: а – L-изомер; б – D-изомер
В живом организме все аминокислоты – L-изомеры, точнее 19 хиральных асимметричных L-аминокислот, а двадцатая аминокислота – гли47
глицин – не имеет хиральности. D-изомеры встречаются довольно редко и
имеют определенные функции, например, могут входить в состав антибиотиков.
Всего живая клетка использует 20 стандартных аминокислот (точнее, 19 аминокислот и одна иминокислота – пролин).
Обозначения аминокислот приведены в таблице 5, а схемы их аминокислотных остатков изображены на рисунке 12.
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Таблица 5 – Названия и обозначения аминокислот
Обозначения
Аминокислоты Амінокислоти
cyr symb
lat
Аланин
Аланін
Ала
A
Ala
Аргинин
Аргінін
Арг
R
Arg
Аспарагин
Аспарагін
Асн
N
Asn
Аспарагиновая Аспарагінова
Асп
D
Asp
кислота
кислота
Валин
Валін
Вал
V
Val
Гистидин
Гістидин
Гис
H
His
Глицин
Гліцин
Гли
G
Gly
Глутамин
Глутамін
Глн
Q
Gln
Глутаминовая
Глутамінова
Глу
E
Glu
кислота
кислота
Изолейцин
Ізолейцин
Иле
I
Ile
Лейцин
Лейцин
Лей
L
Leu
Лизин
Лізин
Лиз
K
Lys
Метионин
Метионін
Мет
M
Met
Пролин
Пролін
Про
P
Pro
Серин
Серин
Сер
S
Ser
Тирозин
Тирозин
Тир
Y
Tyr
Треонин
Треонін
Тре
T
Thr
Триптофан
Триптофан
Трп
W
Trp
Фенилаланин
Фенілаланін
Фен
F
Phe
Цистеин
Цистеїн
Цис
C
Cys
48
Amino acids
Alanine
Arginine
Aspargine
Aspartate
Valine
Histidine
Glycine
Glutamine
Glutamate
Isoleucine
Leucine
Lysine
Methionine
Proline
Serine
Tyrosine
Threonine
Tryptophan
Phenylalanine
Cysteine
Рисунок 12 – Боковые цепи стандартных аминокислотных остатков
В состав аминокислот входят центральный атом α-углерода, Сα, и
три боковые группы: аминогруппа, карбоксильная кислотная группа, и
боковая группа аминокислотного остатка. Каждая аминокислота присое49
диняется пептидной связью между аминогруппой и карбоксилом последующей аминокислоты в цепи.
Двадцать стандартных аминокислот, которые используются в биосинтезе белка, отличаются как химически, так и структурно. Комбинируя эти аминокислоты можно добиться как желаемой формы белковой
глобулы, так и того, чтобы данная глобула была устойчивым образованием.
Кроме того, необходимые для реализации той или иной биохимической реакции боковые группы могут быть размещены в необходимых местах белковой цепи.
Каждая из аминокислот обладает ей одной присущими специфическими свойствами.
Из четырех основных типов биомолекул – белков, нуклеиновых кислот, углеводов и липидов – белки наиболее многоцелевые объекты.
Важное качество белков – их модульность. Они организованы как
линейная цепь аминокислот, которая свернута в определенную структуру
(рисунок 13).
Одна из самых длинных из известных в настоящее время белковых
цепей – аминокислотная последовательность белка титина – имеет более
26 000 аминокислот. С другой стороны существуют пептиды длиной порядка десяти аминокислот – гормоны, которые используются для клеточной сигнализации. Средние же размеры тех водорастворимых белков, чья
концентрация в цитозоле клеток максимальна, составляет 200–500 аминокислот.
Классификация аминокислот. Аминокислоты подразделяют на:
• неполярные (глицин, пролин, аланин, валин, лейцин, изолейцин),
• ароматические (фенилаланин, тирозин, триптофан),
• полярные незаряженные (серин, треонин, цистеин, метионин, аспарагин, глутамин),
• заряженные (отрицательно заряженные: аспарагиновая кислота и глутаминовая кислота; положительно заряженные:
лизин и аргинин).
• гистидин в силу своей специфичности может быть отнесен
как к полярным незаряженным, так и к положительно заряженным аминокислотам.
3.2. СПЕЦИАЛЬНЫЕ АМИНОКИСЛОТЫ
Глицин и пролин. Аминокислоты глицин (Gly, рисунок 14) и пролин (Pro, рисунок 15) выполняют специфические структурные функции
при "строительстве" белковой глобулы.
Рисунок 13 – Схема аминокислотной цепи, которая сворачивается в компактную глобулярную структуру (находится в процессе белкового фолдинга)
50
Рисунок 14 – Схема аминокислоты глицин (Gly)
51
Глицин это самая маленькая аминокислота, не имеющая бокового
радикала. Вследствие этого полипептидная цепь в том месте, где расположен глицин, более лабильна (подвижна).
пептидной цепи двумя ковалентными связями (СН2–αС и СН2–N). Пролин
формирует жесткий изгиб (кинк) в белковой цепи. В коллагене такие кинки обеспечивают формирование тугой тройной белковой спирали.
К специальным аминокислотам можно отнести также аминокислоты
цистеин и метионин.
Цистеин и метионин. Аминокислоты цистеин и метионин содержат атомы серы (рисунки 17,18,20).
Цистеин (Cys) является наиболее реакционно-способной аминокислотой, он содержит тиольную (SH) группу.
Рисунок 15 – Схема аминокислоты пролин (Pro)
Глицин используется в тех местах белковой цепи, которые для достижения наиболее плотной конформации должны быть максимально изогнуты, и там, где другие аминокислоты просто не поместились бы
вследствие плотной упаковки окружающих атомов, как это имеет место,
например, в случае плотного тройного спирального жгута коллагена, изображенного на рисунке 16.
Рисунок 17 – Схема аминокислоты цистеин (Cys)
Два цистеина из разных участков белковой цепи способны образовать ковалентно связанный дисульфидный мостик.
Рисунок 16 – Структурные особенности глицина и пролина
Пролин является единственной циклической аминокислотой (точнее, пролин – это иминокислота), у которой радикал присоединен к поли52
Рисунок 18 – Схема аминокислоты метионин (Met)
53
Цистеин также (как и серин) используется в формировании каталитических активных центров ферментов. Цистеин эффективно взаимодействует c ионами металлов и используется при формировании металосвязывающих центров.
Метионин (Met) имеет гидрофобный атом серы. Именно с метионина (точнее с формилметионина (рисунок 19(а)) начинается синтез любой
белковой цепи.
Рисунок 20 – Структурные особенности цистеина и метионина
3.3. НЕПОЛЯРНЫЕ И АРОМАТИЧЕСКИЕ АМИНОКИСЛОТЫ
а
б
в
Рисунок 19 – Структурные схемы: а – формилметионин, б – гуанидин, в – имидазол
Метионин часто используется подобно гидрофобным алифатическим аминокислотам для обеспечения фолдинга белка.
Аланин, валин, лейцин и изолейцин. Аминокислоты аланин (Ala),
валин (Val), лейцин (Leu) и изолейцин (Ile) (рисунки 21 – 24) являются неполярными алифатическими аминокислотами, боковые цепи которых насыщены углеводородными группами и различаются формой и размером.
Аминокислоты аланин, валин, лейцин и изолейцин обеспечивают
относительную жесткость, негибкость, полипептидной цепи и являются
сильно гидрофобными.
Атом серы является нуклеофильным и может взаимодействовать с
некоторыми типами ионов металла.
Эти свойства цистеина и метионина используются в малом электрон-несущем белке ферредоксин (рисунок 20).
Дисульфидная связь показана в правом верхнем углу ферредоксина,
четыре цистеина удерживают кластер, состоящий из атома железа и четырех атомов серы (кластер показан темно-серым цветом в центре ферредоксина). Два метионина окружают кластер, стабилизируя его внутри
белка.
54
Рисунок 21 – Схема аминокислоты аланин (Ala)
55
Зачастую именно наличие этих гидрофобных аминокислот обеспечивает фолдинг белковой цепи. На рисунке 25 изображено положение
этих аминокислот внутри глобулы инсулина, образуя плотно упакованный
кластер внутри белка.
Рисунок 22 – Схема аминокислоты валин (Val)
Рисунок 23 – Схема аминокислоты изолейцин (Ile)
Рисунок 25 – Структурные особенности изолейцина, лейцина, аланина и валина
Хотя можно представить себе большое количество других подобных аминокислотных остатков, отличающихся числом и расположением
углеводородных групп, но только эти четыре аминокислоты кодируются
генетически в естественных биосистемах.
Рисунок 24 – Схема аминокислоты лейцин (Leu)
56
Фенилаланин, тирозин и триптофан. Аминокислотные остатки
фенилаланина (Phe), тирозина (Tyr) и триптофана (Trp) содержат ароматические группы (рисунки 26 – 29). Так же, как и в случае алифатических аминокислот, эти аминокислоты являются гидрофобными и также
обеспечивают фолдинг белковых цепей.
57
Ароматические кольца этих аминокислот часто располагаются
стопкой друг над другом или над основаниями ДНК (также имеющими
циклическую структуру) и используются для обеспечения специфичности
участков связывания данного белка с другими белковыми молекулами
или нуклеиновыми кислотами.
Тирозин, кроме ароматического кольца, имеет ещё и гидроксильную
группу. Этим обеспечиваются его особые свойства, которые используются для обеспечения взаимодействия с малыми органическими молекулами. Активные центры, в которых присутствует тирозин, одновременно
Рисунок 26 – Схема аминокислоты фенилаланин (Phe)
могут и связываться с гидрофобными участками лигандов, и образовывать водородные связи с лигандами.
На рисунке 29 представлена схема молекулы бактериального порина, погруженного в липидную мембрану. Мембрана изображена на рисунке схематически в виде серого прямоугольника.
Рисунок 27 – Схема аминокислоты тирозин (Tyr)
Рисунок 29 – Структурные особенности фенилаланина, тирозина и триптофана
Ароматические аминокислоты расположены по периметру порина,
образуя целые зоны на поверхности белка, которые взаимодействуют с
Рисунок 28 – Схема аминокислоты триптофан (Trp)
58
гидрофобной внутренней областью биомембраны.
59
3.4. ПОЛЯРНЫЕ НЕЗАРЯЖЕННЫЕ АМИНОКИСЛОТЫ
К полярным незаряженным аминокислотам относятся серин (Ser),
треонин (Thr), аспарагин (Asn), глутамин (Gln) и гистидин (His) (рисунки 30 – 34).
Аминокислотные остатки серина, треонина, гистидина, аспарагина
и глутамина участвуют в образовании водородных связей. Эти аминокислоты, как правило, располагаются на поверхности белковой глобулы, где
они взаимодействуют с окружающей водой (рисунок 35).
Рисунок 32 – Схема аминокислоты аспарагин (Asn)
Рисунок 30 – Схема аминокислоты серин (Ser)
Рисунок 33 – Схема аминокислоты глутамин (Glu)
Рисунок 31 – Схема аминокислоты треонин (Thr)
Рисунок 34 – Схема аминокислоты гистидин (His)
60
61
Полярные незаряженные аминокислоты часто используются для соединения белковых структур между собой и для формирования специфических взаимодействий с другими молекулами.
Гистидин выполняет особые функции. Он содержит имидазольную
группу (рисунок 19(в)), которая может принимать заряженную или нейтральную формы в слегка отличающихся условиях. В нейтральной форме
в гистидине сочетаются одновременно и электрофильный протонированый вторичный азот, который может быть донором водородной связи, и
сильно нуклеофильный третичный азот, который может быть акцептором водородной связи. Поскольку третичный азот зачастую протонируется в цитозоле, то гистидин иногда относят к положительно заряженным
аминокислотам.
Гистидин не часто используется в белках. Главным образом, он участвует в формировании специализированных каталитических активных
центров ферментов. Например, на рисунке 35 показано, как гистидин использован в протеолитическом ферменте трипсине для активации аминокислоты серин.
Обычно гидроксильная группа серина неактивна, но в активированной форме серин участвует в каталитических реакциях, в которых нужно
либо добавить, либо отвести атом водорода.
Гистидин также эффективно взаимодействует с ионами металлов и
используется для формирования специфических металл-связывающих
центров.
3.5. ЗАРЯЖЕННЫЕ АМИНОКИСЛОТЫ
К заряженным аминокислотам относят:
• отрицательно заряженные аминокислоты:
− аспарагиновая кислота (Asp),
− глутаминовая кислота (Glu),
• положительно заряженные аминокислоты:
− лизин (Lys),
− аргинин (Arg).
Аспарагиновая и глутаминовая кислота содержат карбоксильные
кислотные группы (рисунки 36–38).
Рисунок 35 – Структурные особенности гистидина, серина, аспарагина, треонина и глутамина
62
Рисунок 36 – Схема аспарагиновой кислоты (Asp)
63
Рисунок 37 – Схема глутаминовой кислоты (Glu)
В нормальных физиологических условиях при нейтральном рН эти
аминокислотные остатки ионизованы и отрицательно заряжены. Они характерны для поверхности белков (рисунок 38) и часто используются в
биохимическом катализе и для прочного связывания металлических катионов.
Рисунок 39 – Схема одного из четырех кальций-связывающих мотивов спиральпетля-спираль белка кальмодулин
Множество других отрицательно заряженных аминокислот расположены на поверхности белков, где они активно взаимодействуют с окружающей водой (рисунок 38).
Лизин и аргинин. Положительно заряженные аминокислоты лизин
и аргинин имеют основные группы на конце длинной углеводородной цепи (рисунки 40–42).
Рисунок 38 – Структурные особенности аспарагиновой и глутаминовой кислот
Кальций-связывающий регуляторный белок кальмодулин использует три кислотные (отрицательно заряженные) аминокислоты для связывания ионов кальция (рисунок 39).
64
Рисунок 40 – Схема аминокислоты лизин (Lys)
65
В частности, аргинин используется для связывания белков с нуклеиновыми кислотами – на рисунке 42 показан репрессорный белок, связанный с двойной спиралью ДНК.
Длинная гибкая углеводородная цепь аргинина также участвует в
гидрофобных взаимодействиях с другими гидрофобными молекулами.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
Рисунок 41 – Схема аминокислоты аргинин (Arg)
Аминогруппа на конце лизина и гуанидиновая (рисунок 19(б))
группа на конце аргинина ионизованы при физиологических условиях и
нормальном рН и несут положительный заряд. Лизин и аргинин располагаются на поверхности белковых глобул и используются для распознавания отрицательно заряженных молекул.
Рисунок 42 – Структурные особенности лизина и аргинина (темно-серым цветом изображена молекула ДНК)
66
1. Какие функциональные группы имеет каждая аминокислота?
2. В каких условиях молекулы аминокислот приобретают характер
цвиттерионов?
3. Перечислите неполярные аминокислоты.
4. Перечислите ароматические аминокислоты.
5. Перечислите полярные незаряженные аминокислоты.
6. Какие аминокислоты имеют в своем составе гидроксильную
группу?
7. В состав каких аминокислот входит атом серы?
8. Перечислите заряженные аминокислоты.
9. Перечислите структурные и функциональные особенности аминокислоты глицин.
10. Перечислите структурные и функциональные особенности аминокислоты пролин.
11. Перечислите структурные и функциональные особенности аминокислоты цистеин.
12. Перечислите структурные и функциональные особенности аминокислоты гистидин.
13. Перечислите структурные и функциональные особенности аминокислоты метионин.
14. Перечислите структурные и функциональные особенности аминокислоты триптофан.
15. Перечислите структурные и функциональные особенности аминокислоты серин.
16. Перечислите структурные и функциональные особенности аминокислоты фенилаланин.
67
Глава 4
Пептидная связь является жесткой, причем четыре атома, её образующие (Н–N–C=O), лежат в одной плоскости (рисунок 44).
СТРОЕНИЕ БЕЛКОВ
4.1. ПЕРВИЧНАЯ СТРУКТУРА БЕЛКА
Первичной структурой белка (рисунок 43(а)) называется последовательность расположения аминокислотных остатков в полипептидной
цепи.
Рисунок 44 – Пептидная связь. Межатомные расстояния даны в ангстремах
Электронная структура пептидной связи имеет характер резонанса,
охватывающего все четыре атома пептидной группы и обеспечивающего её жесткость, как если бы все связи имели свойства двойных. В результате пептидная цепь может относительно свободно вращаться только
относительно связей α-углеродов, обозначенных "А" и "В" на рисунке 45.
Рисунок 43 – Строение белковых структур: а – первичная структура белковой
цепи; б – α-спираль; в – β-структура
Рисунок 45 – Резонансы в пептидной связи
Макромолекулы белков состоят из одной или нескольких полипептидных цепей, построенных из аминокислотных остатков. На одном, Nконце цепи находится NH2-группа, на другом, С-конце – группа СООН.
Аминокислоты соединяются в полипептид с помощью ковалентных пептидных связей.
Вследствие образования пептидной связи группа H–N становится
потенциальным донором водородной связи, а группа О=С – её акцептором. Наглядно этот процесс можно представить как "перенос" электрона с
азота на кислород.
68
69
4.2. ВТОРИЧНАЯ СТРУКТУРА БЕЛКА
Для описания стереометрии аминокислотных остатков в белках используют так называемые карты Рамачандрана – геодезическое изобра-
Вторичной структурой белка называется упорядоченное строение
полипептидных цепей, обусловленное водородными связями между группами С=О и N–H разных аминокислот.
Жесткость пептидных связей между аминокислотами и топологические отличия в структуре аминокислотных остатков накладывают определенные стерические ограничения на вторичную структуру пептидной
цепи.
жение "разрешённых" и "запрещённых" комбинаций углов φ и ψ для
конкретных белковых конформаций (рисунки 46,47). Пример такого "картографического" изображения показан на рисунке 46(б). Если бы не накладывалось никаких ограничений на стереометрию полипептидной цепи,
Торсионные углы вращения вокруг связей N–Cα и Cα–C главной це-
то торсионные углы φ и ψ могли бы принимать любые значения. В этом
случае точка, соответствующая конформации того или иного аминокислотного остатка могла бы оказаться в любом месте карты Рамачандрана.
пи, показанные на рисунке 46(а), называют соответственно углами φ и ψ.
Стрелки на рисунке указывают направление вращения, ведущее к росту
угла поворота ближней к нам части цепи относительно более отдаленной
её части.
а
б
Рисунок 47 – Стерические ограничения в пептидной цепи: а – "разрешённые"
конформации; б – "запрещённая" конформация. 1 – φ = –90°, ψ = 120°; 2 – φ = –90°,
ψ = –60°; 3 – φ = +90°, ψ = –90°
В действительности допустимы вовсе не любые комбинации углов
а
б
Рисунок 46 – Конформации полипептидной цепи: а – главная цепь полипептида
и боковая группа цистеина на ней; б – карта Рамачандрана. Интенсивность окраски
пропорциональна "разрешённости" соответствующей комбинации торсионных углов
поворота φ и ψ в главной цепи (глубине энергетической "долины")
70
φ и ψ. Это связано с тем, что при изменении обоих углов изменяется и положение атомов в соседних аминокислотных остатках друг относительно
друга.
Сближение в пространстве атомов, особенно объемистых (кислорода, углерода, азота) приводит к их взаимному отталкиванию. Преодоление
этого отталкивания требует значительных энергетических затрат, что де71
лает такую конфигурацию полипептидной цепи неустойчивой, а соответствующую конформацию "запрещённой".
Стерические ограничения – тот факт, что два атома не могут быть в
одно и то же время в одном и том же месте – существенно уменьшает
число возможных комбинаций торсионных углов φ и ψ.
На рисунке 47(а) показаны примеры "разрешённых" конформаций,
соответствующих глубоким "долинам" на карте Рамачандрана, а на рисунке 47(б) энергетически невыгодная "запрещённая" конформация, соответствующая "плато" на карте Рамачандрана.
Периодичность чередования пептидных связей существенным образом определяет геометрию образуемых белковых структур. Именно свойства периодичности пептидных связей в аминокислотной цепи и то, каким
образом располагаются наружу белковой цепочки атомы водорода и
кислорода, определяют только ограниченное количество стабильных конформаций белковой цепи.
В частности, две конформации, представленные на рисунке 43, являются стабильными. В них сочетается минимальность длины цепи с максимальностью числа водородных связей между атомами разных
пептидных групп.
Первая конформация – это α-спираль (рисунки 43(б), 48 и 50(а)).
Цепь свернута в спираль таким образом, что каждый кислород пептидной
группы образует водородную связь с атомом водорода пептидной группы,
расположенной через три аминокислоты от данной (рисунки 48 и 50(а)).
Карта Рамачандрана для α-спиралей представлена на рисунке 49(а).
Вторая конформация – это β-структура, образованная несколькими, расположенными параллельно, цепями (рисунок 43(в)). Каждая из цепей вытянута ровно, а стабильность всей β-структуре обеспечивают
водородные связи между цепями, которые могут формировать как параллельные, так и антипараллельные структуры (рисунок 50(б,в)).
β-Структуры могут взаимодействовать между собой, образуя целые белковые листы. Карта Рамачандрана для β-структур представлена
на рисунке 49(б).
а
б
Рисунок 49 – Карты Рамачандрана: а – для α-спиралей; б – для β-структуры.
Цифрами указаны минимумы: 1 – правая α-спираль (основная); 2 – левая α-спираль
(редкая); 3 – β-структура
Карты
Рисунок 48 – Водородные связи в α-структуре
72
Рамачандрана
допускают
существование
двух
типов
α-спиралей – как правозакрученных (абсолютно доминируют в белках),
так и левозакрученных (практически не встречающихся). Левые спирали
энергетически менее предпочтительны вследствие дополнительных стерических проблем, возникающих из-за наличия боковых L-радикалов
аминокислот.
73
а
б
Рисунок 51 – Схематическое изображение вторичных структур: а – α-спирали,
б – β-структуры
Выделяют надвторичные (супервторичные) структуры (элементарные комплексы) – термодинамически или кинетически стабильные
комплексы α-спиралей и β-структур. В глобулярных белках обнаружены,
например, (β×β)-элементы (два параллельных β-слоя, соединенных сегментом "×"), складка Россмана (βαβαβ-элемент, который образуют два
сегмента α-спирали, вставленные между тремя параллельными β-цепями)
и β-меандр (слой из трех и более антипараллельных β-цепей, "Меандр" –
это название очень извилистой реки в Греции).
4.3. ТРЕТИЧНАЯ СТРУКТУРА БЕЛКА
Рисунок 50 – Вторичная структура белков: а – α-спираль; б – параллельная
β-структура; в – антипараллельная β-структура
α-Спирали образуют достаточно жесткие цилиндрические структуры. На рисунках α-спирали изображаются или как спиральные ленты
или как цилиндры, а β-структуры изображаются как плоские полосы (рисунок 51).
74
Основой функциональности белка, которая требует точной пространственной организации больших ансамблей аминокислот является
третичная структура.
Третичной структурой называют распределение в пространстве
всех атомов белковой молекулы.
Стабильность третичной структуры обусловлена четырьмя типами
взаимодействиями между радикалами.
75
1. Ковалентные связи между остатками двух цистеинов (дисульфидные
мостики) (рисунок 52).
2. Электростатические (ионные) взаимодействия между противоположно заряженными аминокислотными остатками (три радикала со
знаком "+" и два со знаком "–"). Например, положительно заряженная
аминогруппа лизина (NH3+ ) притягивается отрицательно заряженной
карбоксильной группой (СОО–) глутаминовой или аспарагиновой кислоты.
3. Водородные связи, в которых участвуют все аминокислоты, имеющие
гидроксильные, амидные или карбоксильные группы.
4. Гидрофобные взаимодействия между неполярными радикалами и
водным окружением.
труднее сформировать строго гидрофобное ядро. Начиная примерно с молекулярной массы 14–16 кДа, полипептидная цепь формирует два (или
более) домена.
Рисунок 52 – Образование дисульфидного мостика
Свойства этих взаимодействий будут подробно рассмотрены ниже.
Некоторые комбинации α- и β-структур, обеспечивающие функциональную специфичность белков, приведены на рисунке 53.
Третичная структура полностью задается первичной.
Определяющими при образовании третичной структуры являются
гидрофобные взаимодействия в силу неизбирательности (неспецифичности) и многочисленности. Гидрофобное ядро существует у большинства
белков. Решающую роль в стабилизации третичной структуры играет увеличение энтропии воды (растворителя) при сворачивании глобулы.
Свойственный белкам способ организации пространственной структуры – формирование гидрофобного ядра и мозаичной поверхности, содержащей как гидрофильные, так и гидрофобные элементы, –
ограничивает размеры глобулы, поскольку с увеличением её объема
Доменами называют области в третичной структуре белка с определенной структурной автономией. Часто структурная автономия доменов
76
77
Рисунок 53 – Комбинации α-спиралей, β-структур и соединяющих белковых
нитей определяют топологию белков: (1–5) – комбинации α-спиралей; (6–15) – комбинации β-структур; (16–20) – α/β комбинированные третичные структуры белков
дополняется функциональной. Так в ферментах зачастую каталитические
домены структурно отделены от регуляторных доменов.
Наличие доменов создает структурные предпосылки для большей
внутренней гибкости, динамики, белковых молекул, достигаемой смещением доменов относительно друг друга.
4.4. ЧЕТВЕРТИЧНАЯ СТРУКТУРА БЕЛКА
Четвертичной структурой белка называется агрегация двух или
большего числа полипептидных цепей, имеющих третичную структуру, в
олигомерную функционально значимую композицию.
Связи, образующие и поддерживающие четвертичную структуру, те
же самые, что и при образовании третичной структуры, кроме гидрофобных.
Четвертичную структуру имеют около половины белков, в том
числе гемоглобин, иммуноглобулин, инсулин. Почти все ДНК- и РНКполимеразы имеют четвертичную структуру. Множество ферментов имеют четвертичную структуру. Ниже мы подробно рассмотрим пример работы фермента лактатдегидрогеназа, который состоит из четырех
идентичных субъединиц.
Белок – это отдельный полипептид или агрегат нескольких полипептидов, выполняющий биологическую функцию.
Следует подчеркнуть, что полипептид – понятие химическое, а белок – понятие биологическое.
Например, иммуноглобулин состоит из четырех полипептидных цепей, которые по отдельности не являются белками, белок – только их
функциональный агрегат.
2. Архитектурная функция. В той же протеинкиназе А зона связывания субстрата образована двумя доменами, которые при взаимодействии с
фосфатной группой субстрата сближаются, закрывая его от окружающего
растворителя, так что реакция протекает при полном его отсутствии.
3. Обеспечение множественных взаимодействий белка с протяженными структурами. За счет существования четвертичной структуры иммуноглобулины (антитела) объединяют в одной молекуле два идентичных
центра связывания антигена. Кооперативность взаимодействия таких центров с макромолекулярными антигенами, например бактериальными
стенками, делает комплексы антиген-иммуноглобулин гораздо более
прочными, чем это наблюдалось бы для мономерного белка.
4. Регуляторная функция. Главная функциональная особенность четвертичной структуры, по-видимому, смысл её существования, состоит в
том, что относительно слабые взаимодействия между субъединицами, характер которых существенно зависит от третичной структуры каждой из
них, особенно удобны для регуляторных воздействий, управления активностью белков. Изменения в третичной структуре какого-либо домена,
вызванные его взаимодействием с субстратом или иным лигандом, вследствие относительной слабости междоменных контактов, передаются на
зону его контакта с другим доменом, изменяя характер этой зоны. Такое
изменение приводит к перестройке всей четвертичной структуры и
обеспечивает передачу эффекта от одного домена к другим.
Таким образом, иерархию белковых структур можно изобразить в
виде схемы, представленной на рисунке 54.
4.5. ФОЛДИНГ БЕЛКОВ
1. Объединение нескольких взаимосвязанных функций в единой структуре. Например, фермент протеинкиназа А состоит из двух субъединиц,
одна из которых катализирует перенос фосфата АТФ на белок, а другая
является регуляторной.
Синтезируемые в клетке полипептидные цепи, образованные в результате последовательного соединения аминокислотных остатков, представляют собой как бы полностью развернутые белковые молекулы. Для
того чтобы белок приобрел присущие ему функциональные свойства,
цепь должна определенным образом свернуться в пространстве, сформировав функционально активную (нативную) структуру.
78
79
Основные функции четвертичной структуры белка.
Несмотря на громадное число пространственных структур теоретически возможных для отдельной аминокислотной последовательности,
сворачивание (фолдинг) каждого белка приводит к образованию единственной нативной конформации.
а
б
в
г
Рисунок 54 – Иерархия белковых структур: а – первичная структура; 1 – аминокислоты; б – вторичные структуры; в – третичная структура; г – четвертичная структура
Парадокс Левинталя. В 1968 г. Сайрус Левинталь оценил время, за
которое белковая цепь смогла бы реализовать ту единственную из возможных конформаций, которая и является нативной, функциональной,
белковой конформацией.
Пусть каждый аминокислотный остаток имеет около 10 возможных
конформаций, тогда цепь из 100 остатков имеет порядка 10100 возможных
конформаций. Поэтому белок должен искать "свою" пространственную
структуру среди порядка 10100 возможных. И, поскольку переход из одной
конформации в другую занимает как минимум 10–13 секунды, простой перебор всех 10100 структур должен был бы занять порядка 1080 лет, на фоне
которых время жизни нашей Вселенной – 1010 лет – величина бесконечно
малая.
Таким образом, парадокс заключается в том, что, с одной стороны,
нативная пространственная структура по всем тестам ведет себя как самая стабильная из всех существующих структур цепи: белковая цепь по-
80
падает в нее при разных кинетических процессах (и при сворачивании на
рибосоме в процессе биосинтеза, и после прохода сквозь мембрану, и при
сворачивании в пробирке (ренатурации), – чем бы и как бы она ни была в
этой пробирке развернута). С другой стороны, нет никаких гарантий, что
эта структура – самая стабильная из всех возможных: у белковой цепи
просто нет времени на то, чтобы убедиться в этом.
Левинталь предположил, что самоорганизующийся белок следует
по какому-то специальному "пути сворачивания", и та структура, где этот
путь заканчивается, и является его нативной структурой. Нативная структура белка определяется не стабильностью, не термодинамикой, а кинетикой, т. е. она соответствует не глобальному, а наиболее быстро
достижимому минимуму свободной энергии цепи.
Сворачивание белковой цепи ведет к падению её энтропии (из-за
роста упорядоченности цепи) и энергии (из-за образования в цепи контактов между сближающимися звеньями). Падение энтропии повышает, а
падение энергии понижает свободную энергию цепи.
Если, по ходу сворачивания, цепь должна очень близко подойти к
своей финальной структуре перед тем, как начнут возникать стабилизирующие эту структуру контакты (т.е. цепь должна потерять почти всю
свою энтропию перед тем, как начнет выигрываться энергия), – то повышение свободной энергии на первом этапе фолдинга будет пропорциональным числу звеньев в цепи, т.е. очень большим, а сворачивание цепи –
чрезвычайно медленным. Именно такая картина (проигрыш всей энтропии до начала выигрыша энергии) лежит в основе "парадокса Левинталя",
утверждающего, что белковая цепь никак не может – даже за время жизни
Вселенной – найти свою самую стабильную структуру.
Однако, если путь сворачивания таков, что по ходу его падение энтропии практически тут же компенсируется падением энергии, – то он
не перекрыт высоким свободно-энергетическим барьером, и сворачивание
идет быстро. Кроме того, как мы видели выше, даже для одной аминокислоты в белковой цепи разрешены не все конформационные положения, а
только те, которые соответствуют минимумам на карте Рамачандрана
81
(рисунок 46(б)). Потому изначально ход фолдинга "управляется" "скатыванием" системы в энергетические "долины" карты Рамачандрана.
Образование пространственной структуры – процесс спонтанный,
не требующий ни дополнительной информации, ни источника энергии.
Структуру белка определяет его аминокислотная последовательность
(а значит генетический код), а не работа сложных синтезирующих машин
в клетке. Основная задача всех внутриклеточных приспособлений и помощников – оберегать сворачивающийся белок от нежелательных контактов, которые могут помешать формированию глобулы.
Полипептидная цепь строится путем последовательного роста на
рибосоме от N-конца к С-концу. Фолдинг белка начинается уже со стартовой конформации, поддерживаемой рибосомой. Поиск путей сворачивания идет последовательно с растущего N-концевого участка, при этом в
процессе сворачивания С-конец фиксирован.
Рибосома может способствовать определенному пути сворачивания. Благодаря существующей внутри клетки высоко координированной
системе регуляции, полипептидная цепь с самого момента своего "рождения", сходя с рибосомы, попадает под контроль факторов, которые, не изменяя специфического пути сворачивания (определяемого генетическим
кодом), обеспечивают оптимальные условия для реализации быстрого и
эффективного образования нативной пространственной структуры.
Однако, несмотря на "избранный" путь, определенный рибосомой,
те же пространственные структуры белков получаются и после транслокации более или менее развернутой цепи через биомембрану, и in vitro,
при сворачивании (ренатурации) целой белковой цепи из развернутого
состояния. Это значит, что детальная последовательность действий не
играет решающей роли при сворачивании белка.
Белковая цепь самопроизвольно сворачивается в функциональную
нативную конформацию, которая является энергетически наиболее выгодной, и все параметры которой задаются исключительно первичной
структурой белка. Эксперименты по денатурации и ренатурации белковой
цепи под действием обратимых изменений температуры, кислотности
среды или наличия особых химикалий, ослабляющих, например, дисуль-
фидные связи, показали, что сворачивание происходит самопроизвольно и
никакие дополнительные белковые и небелковые факторы не нужны для
фолдинга.
82
83
Стадии фолдинга. Процесс сворачивания имеет иерархическую
природу, в нем можно выделить четыре стадии.
1. Очень быстрое формирование элементов вторичной структуры, служащих как бы "зародышами" для образования более сложных архитектурных мотивов (за десятую долю микросекунды альфа-спираль
охватывает пептид из 20–30 остатков).
2. Специфическая быстрая ассоциация некоторых элементов вторичной
структуры с образованием супервторичной структуры: сочетания нескольких α-спиралей, нескольких β-цепей либо смешанные ассоциаты
данных элементов.
3. Формирование "расплавленной глобулы" (создание основных элементов третичной структуры – сочетание α-спиралей, β-тяжей, соединяющих петель и образование гидрофобного ядра молекулы) Молекула
приобретает пространственную структуру, близкую к структуре нативного белка. Вместе с тем, она ещё не обладает присущей данному белку
функциональной активностью. Это состояние отличается от нативного
меньшей степенью упорядоченности структуры (рисунок 55(а)).
а
б
Рисунок 55 – Схема формирования глобулы: а – расплавленная глобула; б – нативная глобула
В расплавленной глобуле существуют поры, в которые проникает вода. Отсутствие ряда специфических взаимодействий приводит к
тому, что ориентация подвижных петель несколько отличается от более "жесткой" финальной нативной структуры. В целом молекула более лабильна и склонна к "слипанию" (агрегации) с другими такими же
молекулами. Такая неспецифическая агрегация может уменьшать число молекул белка, находящихся на правильном пути сворачивания, то
есть снижать эффективность этого процесса. Как показали модельные
эксперименты, проведенные in vitro, образование "расплавленной
глобулы" происходит значительно быстрее, чем её переход в нативную
структуру.
4. Формирование нативной структуры белка (рисунок 55(б)). Эта стадия,
связанная с перебором разных конформаций отдельными радикалами
аминокислот, является, самой медленной стадией процесса сворачивания (от секунд до десятков минут).
Денатурация белка. Концепция "расплавленной глобулы" послужила ключом к пониманию особенностей процесса денатурации белков
(термической или под воздействием денатурантов, резко изменяющих рН
раствора). Экспериментально установлено, что денатурация малых белков
является кооперативным переходом с одновременным и резким,
"S-образным" изменением многих характеристик молекулы. Например,
резко изменяется энтальпия (рисунок 56), поэтому её производная C p
кость Cmax при температуре перехода Tm отсчитывается от середины отрезка ΔCp .
S-образность экспериментальных кривых показывает, что соответствующие характеристики молекулы изменяются в диапазоне от тех, что
характерны для нативного белка, до тех, что характерны для белка денатурированного. Узость этих S-образных кривых свидетельствует о кооперативности перехода, т.е. о том, что он охватывает сразу много
аминокислотных остатков. При таком переходе только начальное (нативное) и конечное (денатурированное) состояние наблюдаются в заметных
количествах, а "полуденатурированных" молекул практически нет. Иначе
говоря, переход "все-или-ничего" является микроскопическим аналогом
фазового перехода первого рода в макроскопических системах (например
– плавления кристалла). Однако – в отличие от истинного фазового перехода – S-образность белкового перехода "все-или-ничего" имеет не нулевую, а конечную ширину, так как этот переход охватывает не
макроскопическую, а микроскопическую, очень небольшую систему.
имеет максимум в области перехода. Скрытая теплота перехода Q изображена на рисунке 56(б) в виде заштрихованной области
Q=
T Tm
∫
Cp d T .
T Tm
Теплоемкость денатурированного белка выше теплоемкости нативной глобулы ( ΔCp ), поскольку в денатурированном белке гидрофобные
а
б
Рисунок 56 – Кривая плавления типичного белка: а – температурная зависимость энтальпии; б – температурная зависимость теплоемкости.
аминокислоты экспонированы в растворитель. Максимальная теплоем-
При повышении температуры сначала формируется расплавленная
глобула – порядок ещё сохранен, начинается только "раздвижение" элементов вторичной структуры, нековалентные связи между ними ослабе-
84
85
вают и в промежутки между ними начинают входить молекулы воды, но
боковые радикалы аминокислот ещё не освободились настолько, чтобы
быть способными к поворотной изомеризации. Такое начальное расширение глобулы энергетически невыгодно, поскольку при этом энергия глобулы растет (поскольку части глобулы уже расходятся, а энтропия ещё не
повышается. Поэтому, при таком малом расширении свободная энергия
глобулы растет. Когда же расширение достигает такой величины, что освобождаются боковые группы аминокислот и становится возможной их
поворотная изомеризация, это приводит к резкому росту энтропии и падению свободной энергии. Причем, поскольку все боковые группы аминокислот прикреплены к одной пептидной цепи, то "включение"
поворотной изомеризации происходит для всех боковых радикалов практически одновременно. В результате денатурация белка при изменении
внешних условий происходит не постепенно, а скачком, – по принципу
"всё или ничего".
То есть белок, не меняясь, терпит изменение внешних условий до
некоторого предела, – а потом плавится, как микроскопическое твердое
тело, весь сразу. Такая устойчивость и твердость белка, в свою очередь,
обеспечивает надежность его работы в организме.
Таким образом, фазовый переход между нативным и денатурированным состояниями объясняется скачкообразным ростом энтропии
(и прежде всего – энтропии боковых групп) при расширении глобулы, а
его фазовый, кооперативный характер связан с тем, что боковые группы
прикреплены к главной цепи и не могут раскрепощаться поодиночке.
Соответственно, фолдинг белковой цепи нагляднее всего представлять как запущенный обратно во времени процесс денатурации со всеми
этапами денатурации, но происходящими в обратном порядке.
Фолдинг гомологичных белков и белковая инженерия белков.
Не все белковые последовательности сворачиваются в стабильные
структуры. По современным оценкам только небольшая часть возможных комбинаций аминокислот способны формировать стабильные структуры. Исследователи считают, что есть всего лишь порядка 1000 способов
свернуть белковую нить в стабильную структуру.
86
Известно очень много примеров, когда подобные, гомологичные
аминокислотные последовательности сворачиваются в подобные трехмерные структуры, отличающиеся лишь в деталях.
Так, например, аминокислотная последовательность в гемоглобинах,
синтезируемых различными животными, варьируется очень сильно. Из
140-150 аминокислот аминокислотной цепи гемоглобина только две аминокислоты повторяются во всех вариативных формах: гистидин, который
напрямую скоординирован с активным ионом железа в геме, и фенилаланин, который необходим для правильной ориентации гема-кофактора. Все
другие аминокислоты могут изменяться, что позволяет модифицировать
функции гемоглобинов (например, сродство к кислороду может отличаться в 100 000 раз), или просто вследствие дрейфа генов.
Несмотря на такой огромный диапазон вариабельности гемоглобинов, все они принимают подобную трехмерную функциональную структуру в ходе фолдинга.
Предсказание структуры достаточно надежно для гомологичных
аминокислотных последовательностей. Для последовательностей с
30-40% идентичных аминокислот существует высокая вероятность того,
что их трехмерная структура будет подобна до такой степени, что возможно будет применить современные методики белкового моделирования. Это благоприятное для биотехнологии обстоятельство позволяет
предсказывать множество новых белковых структур.
Однако белковые инженеры сталкиваются с другого рода проблемой. Вышеупомянутая статистика справедлива только для природных
биомолекул, чья структура была оптимизирована эволюцией для эффективного фолдинга. Точечные изменения структуры могут быть фатальны для функциональности и фолдинга белка, хотя этот белок все ещё
будет демонстрировать высокую степень гомологичности к белкам демонстрирующим успешный фолдинг.
Поэтому, при попытках модификации существующего белка для
достижения новой функциональности, изменения следует вносить небольшими порциями, каждый раз проверяя, сохраняет ли измененный белок способность к функциональному фолдингу.
87
4.6. МЕХАНИЗМЫ РЕГУЛЯЦИИ ФОЛДИНГА
Самопроизвольный фолдинг является очень медленным процессом,
и нерационально синтезировать белковые цепи, которые долгое время не
будут принимать активную форму. Кроме того, фолдингу могут препятствовать процессы агрегации белковых цепей, чего не наблюдается
in vivo.
Для исключения агрегации расплавленных глобул в физиологических условиях синтеза полипептидной цепи в клетке задействованы специальные механизмы регуляции формирования пространственной
структуры белка.
Механизм регуляции скорости превращения расплавленной
глобулы в нативную структуру. Установление "оптимального набора"
специфических взаимодействий, стабилизирующих нативную конформацию, связано с необходимостью структурных перестроек, происходящих
относительно медленно. Скорость сворачивания и образование специфических для данного белка внутримолекулярных связей управляется ферментами.
Например, цис-транс-изомеризация пептидной связи, предшествующей остатку пролина, приводящая к повороту цепи на 180° вокруг
C–N связи, идет чрезвычайно медленно. In vivo она ускоряется благодаря
действию специального фермента – пептидил-пролил-цис/трансизомеразы. Другой фермент, ускоряющий процесс сворачивания – протеин-дисульфид-изомераза – катализирует образование и изомеризацию дисульфидных связей. Ускоряя стадии, лимитирующие скорость
сворачивания, ферменты способствуют удержанию белка на правильном
пути приобретения нативной структуры, снижая риск протеолитической
деградации и агрегации лабильных промежуточных форм.
ясь с развернутой или частично развернутой конформацией полипептидной цепи, не дают ей "запутаться", образовать неправильные структуры.
Они удерживают частично развернутый белок, способствуют его переносу в разные субклеточные образования, а также создают условия для его
эффективного сворачивания.
Эти белки получили название "молекулярные шапероны", образно
отражающее их функцию (chaperon – пожилая дама, сопровождающая
молодую девушку на балы, наставник, сопровождающий группу молодежи). К настоящему времени описано несколько классов шаперонов, различающихся по структуре и специфическим функциям.
Все шапероны являются так называемыми "белками теплового шока", синтез которых резко увеличивается в стрессовых для клетки ситуациях. Поэтому сокращенное название этих белков – hsp (heat shock
proteins). Однако и в нормальных условиях каждая клетка содержит определенный набор шаперонов, необходимых для её жизнедеятельности.
Классификация шаперонов основана на величине молекулярной массы
составляющих их субъединиц, которая варьирует от 10 кДа (hsp10) до 90
кДа (hsp90) и выше.
По характеру выполняемых этими белками функций их можно разделить на два больших семейства – шапероны, или hsp70 (рисунок 57), и
шаперонины, к которым относятся hsp60 и hsp10 (рисунок 58).
Механизм защиты полипептидной цепи от неспецифической
агрегации. В клетке существует особая категория белков, основной
функцией которых является обеспечение правильного характера сворачивания полипептидных цепей в нативную структуру. Эти белки, связыва-
Рисунок 57 – Схема шаперона hsp70. Шаперон состоит из двух доменов: левый
связывается с АТФ, в результате чего правый домен прикрепляется к полипептидной
цепи участком, окрашенным на рисунке белым цветом
88
89
Шапероны hsp70 связываются с отдельными участками полипептидной цепи и удерживают её в развернутом состоянии.
В клетках эукариот шапероны выполняют важную роль в транспорте белков через мембраны митохондрий, хлоропластов и эндоплазматического ретикулума. Такой транспорт необходим, так как многие белки
клеточных органелл синтезируются в цитоплазме, а окончательно сворачиваются в месте своей постоянной локализации, поэтому разворачивание
– обязательное условие проникновения белковой молекулы через мембрану. Митохондриальный матрикс содержит собственные шапероны,
"подхватывающие" пересекающий мембрану белок и способствующие его
"втягиванию" в митохондрию.
липептидной цепи, перешедшей на шаперонин с шаперона hsp70. Иногда
такую "пробирку" называют "ячейкой Анфинсена".
Шаперонины являются полостями с гидрофобной внутренней поверхностью. Вновь синтезированный белок, "притягиваемый" гидрофобностью внутренней поверхности полости шаперонина, входит внутрь этой
полости. После того как в канал молекулы шаперонина попадает полипептидная цепь, вход прикрывает hsp10 – белковое кольцо, построенное
из семи субъединиц, и единичная полипептидная цепь оказывается полностью изолированной. Присоединение "крышки" hsp10 индуцирует изменение конформации шаперонина, сопровождающееся поворотом доменов
из которых построены стены полости. Такое изменение конформации
приводит к тому, что многие из гидрофобных аминокислот "втягиваются"
в стены шаперонина, и увеличивается объем полости.
Белок, утратив стабилизирующие "опоры" в стенах шаперонина, теперь получает возможность реализовывать медленные стадии сворачивания с очень высоким выходом нативного белка.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
а
б
в
Рисунок 58 – Схема шаперонина hsp60: а – вид сверху; б – вид сбоку; в – разрез.
1 – гидрофобные участки; 2 – участок связывания АТФ; 3 – полость
В отличие от довольно просто построенных шаперонов (состоящих
из одного-двух доменов), шаперонины представляют собой сложные олигомерные структуры. Наиболее изученные hsp60 митохондрий, а также
клеток E. coli, построены из 14 субъединиц, организованных в два семичленных кольца, лежащих одно под другим.
В центре построенного таким образом цилиндра имеется полость –
канал (диаметром 45 ангстрем), в котором и происходит сворачивание по90
1. Что называется первичной структурой фермента?
2. Какие связи обеспечивают стабильность первичной структуры
фермента?
3. Какова роль резонансов в формировании пептидных связей? Какие атомы охватывает резонанс в пептидной связи?
4. Что называется вторичной структурой фермента?
5. Какие взаимодействия обеспечивают стабильность вторичной
структуры фермента?
6. В чем состоит специфика формирования вторичной структуры
фермента в случае α-спирали?
7. В чем состоит специфика формирования вторичной структуры
фермента в случае β-структуры?
8. Что называется третичной структурой фермента?
9. Какие взаимодействия обеспечивают стабильность третичной
структуры фермента?
91
10. Что называется доменом?
11. Как образуются дисульфидные мостики?
12. Что называется четвертичной структурой фермента?
13. Какие взаимодействия обеспечивают стабильность четвертичной
структуры белка?
14. В чем сходство и различие понятий белок и полипептид?
15. Каковы основные функции четвертичной структуры белка?
16. В чем заключается парадокс Левинталя?
17. Какие существуют стадии фолдинга молекулы фермента?
18. В чем сходство и отличие расплавленной и нативной глобулы молекулы фермента?
19. Перечислите механизмы регуляции формирования пространственной структуры фермента в ходе фолдинга.
20. Что такое молекулярные шапероны?
21. В чем сходство и различие шаперонов и шаперонинов?
Глава 5
ФИЗИЧЕСКИЕ ВЗАИМОДЕЙСТВИЯ В ФЕРМЕНТАХ
Природные биомолекулы сконструированы так, чтобы быть стабильными на протяжении биологически необходимого промежутка времени. Большинство ферментов в живой клетке функционируют всего
несколько секунд, и крайне редко создаются ферменты для работы в течении более чем одного года. Биомолекулярные комплексы собираются быстро, используются для специальных задач, а затем разбираются,
обеспечивая тем самым клетку исходными материалами для строительства новых структур. Правилом является планируемая при сборке пригодность для утилизации.
Для синтеза объектов с такими свойствами идеальными являются
органические молекулы на основе углерода. Органические молекулы
обеспечивают большой набор взаимодействий в водном окружении. Они
стабильны при физиологических температурах, но ковалентные связи в
них не слишком прочные, что позволяет осуществлять быструю пере92
стройку молекул в течение секунд. Комбинируя углерод с несколькими
другими атомами – кислородом, водородом, азотом, серой, фосфором –
может быть синтезировано бесконечное разнообразие молекул с различными химическими свойствами.
Структура и свойства органических молекул можно понять, используя простую эмпирическую модель, которой химики и биологи используют уже много десятилетий. Это конечно, не то полное описание, которое
обеспечивает квантовая механика, но этого достаточно для понимания тех
исходных взаимодействий, которые и формируют форму, и стабилизируют биомакромолекулы.
Такое упрощенное описание включает три основных модели.
Во-первых, ковалентное связывание соединяет атомы, формируя
стабильные структуры с определенной геометрией.
Во-вторых, несколько типов нековалентных сил контролируют
взаимодействия внутри молекул и между молекулами.
И, в-третьих, особые свойства воды кардинально модифицируют
форму и стабильность молекул. Характерная энергия различных взаимодействий приведена в таблице 6.
Таблица 6. Энергия взаимодействий в макромолекулах.
кал/моль
Ковалентная связь
> 50
Ван-дер-ваальсовые силы
<1
Водородная связь
1–7
Электростатические взаимодействия
1–6
Гидрофобные взаимодействия
2–3
0,6
Средняя тепловая энергия при 37°С
5.1. ОСОБЕННОСТИ КОВАЛЕНТНЫХ СВЯЗЕЙ
Самыми сильными взаимодействиями в биомолекулах являются ковалентные связи, которые образуются между атомами благодаря кванто93
вомеханическому обобществлению электронов. При физиологических
температурах ковалентные связи стабильны. Для того чтобы их сформировать или разорвать требуется значительная энергия.
Прочность большинства органических материалов определяется
именно ковалентными связями. Например, шелк формируется многими
длинными нитями (цепочками) ковалентно связанных атомов, сплетенными в жгуты. Прочность шелка определяется этими ковалентными связями. Эластичность шелка является следствием того, что отдельные
одномерно связанные нити легко скользят друг относительно друга, поскольку они не связаны ковалентно между собой.
Если же сформировать трехмерную систему ковалентных связей,
такую, как в углеродной решетке алмаза, образуется самый прочный из
минералов, который выдерживает максимальные нагрузки, приложенные
в любом направлении.
Ковалентные связи жесткие и направленные. Геометрия ковалентных связей определяется квантовомеханическим распределением электронной плотности в атомах.
Для описания структурных свойств большинства органических молекул пользуются наглядными моделями ковалентных связей в основе которых, конечно же, лежит строгое квантовомеханическое описание
межатомных взаимодействий. Эти модели сродни тем шаростержневым
конструкторам, из которых собирают объемные модели молекул.
Однако для более глубокого понимания природы ковалентных связей и при попытках встраивания в органические молекулы более экзотических атомов необходимо более детально изучать квантовую механику и
квантовую химию.
Атомы углерода (С) образуют четыре связи с окружающими атомами, формируя тетраэдрические структуры. В некоторых соединениях
углерод способен образовывать две (или даже три) связи с одним атомом,
образуя двойную связь. Кислород (О) образует две связи под углом порядка 100° или двойную связь с одним атомом. Азот (N) образует три
связи. Сера (S) образует две связи. Фосфор (Р) в биомолекулах участвует
в составе фосфатной группы, в которой он окружен четырьмя атомами
94
кислорода. Стабильные органические молекулы, как правило, имеют углеродный скелет, а присоединенные атомы азота и кислорода, как правило, пространственно разнесены и не соединены друг с другом ковалентно.
Кроме того, обычно менее стабильными являются молекулы, в которых
сильно искажена нормальная геометрия атомных орбиталей, например,
такой является треугольная молекула из трех атомов углерода.
Геометрия взаимодействий посредством ковалентных связей четко
определена и относительно жестка. Длина связей варьируется только на
доли ангстрема, а вариации углов между двумя связями редко превышают несколько градусов.
В то же время, для многих типов связей разрешено вращение вокруг
связей. Вообще говоря, хотя такое движение, как и все в квантовом мире,
является последовательными перескоками системы из одного состояния в
другое, но, поскольку барьеры при таких перескоках малы, то в молекулярной биологии одиночные связи принято рассматривать как оси вращения. Однако двойные и тройные связи, при образовании которых
обобществляются дополнительные электроны, являются жесткими.
В действительности все не так просто. Вышеперечисленные простые правила должны быть скорректированы с учетом явлений гибридизации и резонансов, которые объясняют некоторые необычные аномалии.
Резонансы существенно снижают гибкость молекулярных связей.
Примером этого является пептидная связь (рисунок 44).
Вследствие гибридизации вся пептидная группа является жестким
образованием, лежащим в одной плоскости, хотя могло бы показаться,
что в ней возможно вращение вдоль HN–CO связи.
Наглядно этот процесс можно представить как "перенос" электрона
с азота на кислород, при котором вместо одинарной HN–CO связи формируется двойная. В действительности электронная структура опять-таки
соответствует промежуточному между этими крайностями состоянию,
она имеет характер резонанса, охватывающего все четыре атома пептидной группы и обеспечивающего её жесткость, как если бы все связи
имели свойства двойных. В результате пептидная цепь может относи-
95
тельно свободно вращаться только относительно А и В связей αуглеродов (рисунок 45).
5.2. НЕКОВАЛЕНТНЫЕ ВЗАИМОДЕЙСТВИЯ
Нековалентные взаимодействия являются определяющими в формировании функциональной структуры биологических макромолекул и
клеточных компонентов. Силы нековалентных межмолекулярных взаимодействий являются короткодействующими – они проявляются на расстояниях менее 10–9м.
Нековалентные взаимодействия (таблица 6) подразделяют на:
(1)
(2)
(3)
(4)
электростатические (или ионные) взаимодействия,
ван-дер-ваальсовые силы,
водородную связь,
гидрофобные силы.
Рассмотрим взаимодействие двух молекул, одна из которых расположена в начале координат (рисунок 59).
F
FО
F=FО+FП
10–9
r0
а
r, м
FП
U
б
10–9
r0
r, м
Umin
Рисунок 59 – Межмолекулярное взаимодействие: а – сила межмолекулярного
взаимодействия; б – потенциальная энергия
96
Сила взаимодействия молекул – это равнодействующая сил притяжения FП (они преобладают на больших расстояниях) и сил отталкивания
FО (они доминируют на малых расстояниях). На расстоянии r = r0 эти силы уравновешивают друг друга и F = 0 .
Таким образом, расстояние r0 – это равновесное расстояние между
молекулами, на котором бы они находились в отсутствие теплового движения. Потенциальная энергия взаимодействия молекул U минимальна в
состоянии устойчивого равновесия при r = r0 (рисунок 59(б)).
Ван-дер-ваальсовые взаимодействия имеют электромагнитную
природу и определяются взаимодействием электрических диполей молекул.
В зависимости от того, обладают ли взаимодействующие молекулы
электрическим дипольным моментом или последний возникает вследствие поляризации оболочек, существуют различные типы ван-дерваальсовых сил:
1) диполь-дипольное взаимодействие полярных молекул,
2) индукционное взаимодействие диполя полярной молекулы с индуцированным диполем другой молекулы,
3) дисперсионное взаимодействие индуцированных диполей двух
молекул.
Диполь-дипольное взаимодействие дипольного момента полярной молекулы с электрическим полем, создаваемым другой полярной молекулой, может иметь характер притяжения (рисунок 60(а)) или
отталкивания (рисунок 60(б)) в зависимости от взаимной ориентации диполей. Таким образом, диполь-дипольное взаимодействие приводит к
ориентационной упорядоченности молекул. С другой стороны, тепловое
движение молекул разупорядочивает ориентацию молекул.
Поэтому диполь-дипольное взаимодействие зависит от температуры
– величина энергии диполь-дипольного взаимодействия, U dd , обратно
пропорциональна T .
97
Усредняя энергию взаимодействия двух диполей по всем возможным
взаимным ориентациям с учетом теплового движения, можно получить
выражение для средней энергии взаимодействия двух молекул с постоянными дипольными моментами μ1 и μ 2 , находящихся на расстоянии R
друг от друга
U dd ( R) = −
2
μ12μ 22 1
.
3k BT (4πε0 ) 2 R 6
–
+
–
+
а
в
д
–
+
+
–
б
г
е
Рисунок 60 – Схема ван-дер-ваальсовых взаимодействий: а,б – дипольдипольное взаимодействие; в,г – индукционное взаимодействие; д,е – дисперсионное
взаимодействие
Индукционное взаимодействие возникает тогда, когда молекула,
обладающая постоянным дипольным моментом (рисунок 60(в,г), черная
стрелка), наводит в другой молекуле, неполярной или полярной, так называемый индуцированный дипольный момент (рисунок 60(в,г), светлая
стрелка).
Взаимодействие постоянного диполя одной молекулы и наведенного
им диполя второй понижает потенциальную энергию системы на величину, называемую энергией индукционного взаимодействия
98
U ind ( R) = −
αμ 2 1
,
8π 2 ε 0 R 6
где α – поляризуемость молекулы, в которой индуцируется диполь.
Индукционное взаимодействие не зависит от температуры, так
как ориентация наведенного диполя не может быть произвольной, она однозначно определяется направлением постоянного диполя. Индукционное
взаимодействие существенно только для молекул со значительными поляризуемостями.
Дисперсионное взаимодействие индуцированных диполей характерно для атомов и молекул, у которых нет не только дипольного, но и
квадрупольного, октупольного и других электрических моментов. Осцилляция электронного облака молекулы позволяет рассматривать её как частицу, имеющую мгновенный дипольный момент, который постоянно
меняет свою величину и направление.
Предположим, что в данный момент времени (рисунок 60(д)) электронная конфигурация молекулы соответствует мгновенному диполю μ1 ,
представленному темной стрелкой. Этот диполь поляризует другую молекулу и индуцирует в ней мгновенный диполь μ 2 , изображенный светлой
стрелкой. Взаимодействие диполей обеспечивает притяжение молекул.
Хотя направление диполя в первой молекуле будет продолжать изменяться, индуцированный диполь во второй молекуле будет подстраиваться под эти изменения (рисунок 60(е)), и вследствие такой
корреляции эффект притяжения не усреднится до нуля.
Энергия дисперсионного взаимодействия пропорциональна поляризуемостям α1 и α 2 обеих молекул и, так же, как энергии дипольдипольного и индукционного взаимодействий, обратно пропорциональна
шестой степени расстояния между молекулами
U disp ( R ) = −
1
3I1I 2 α1α 2
,
2
16π 2( I1 + I 2 ) R 6
где I1 , I 2 – потенциалы ионизации двух молекул.
99
Ван-дер-ваальсовые взаимодействия хорошо описываются потенциалом Ленарда-Джонса (который часто называют потенциалом "(12,6)" –
"двенадцать-шесть") (рисунок 61(а)).
В этой форме параметр ε является глубиной минимума на кривой
(рисунок 61(а)), который соответствует равновесному расстоянию между
молекулами
Re = 6 2 ⋅ σ .
а
б
Рисунок 61 – Ван-дер-ваальсовое взаимодействие: а – потенциал ЛенардаДжонса, б – ван-дер-ваальсовое представление молекулярного комплекса
Зависимость потенциальной энергии V (R ) от расстояния R в потенциале Ленарда-Джонса имеет вид
V ( R) =
C12 C6
−
,
R12 R 6
где C12 и C6 – константы.
При малых R отталкивание (член +
C12
) преобладает над притяR12
C6
).
R6
Часто (12,6)-потенциал записывают в форме
жением (член −
Вместе ван-дер-ваальсовые силы притяжения и паулевские силы отталкивания удерживают атомы на некотором расстоянии друг от друга.
На рисунке 61(б) показан комплекс из двух близкорасположенных аминокислот, удерживаемых вместе ван-дер-ваальсовыми силами притяжения,
но предохраняемым от перекрытия молекул паулевскими силами отталкивания. Обычно эти пары сил визуализируют используя ван-дер-ваальсовое представление молекул (так называемую модель "spacefilling"). В вандер-ваальсовых моделях каждый атом изображается в виде сферы соответствующего радиуса так, чтобы изобразить пространственное расположение атомов, при котором достигается оптимальный баланс между вандер-ваальсовым притяжением и паулевским отталкиванием.
Вандерваальсово–паулевские взаимодействия существенно увеличивают стабильность биомолекул. Энергия каждого из взаимодействий
мала, но суммарно эти малые энергии складываются в значительную величину для всей биомолекулы.
Ван-дер-ваальсовые силы явно проявляются в виде трения и адгезии
(слипания) при соприкосновении двух поверхностей. Например, насекомые и ящерицы гекконы используют дисперсионные силы между поверхностями их лапок и вертикальными поверхностями стен, чтобы
перемещаться по ним.
Водородные связи. Водородные связи играют главную роль в обеспечении стабильности биомолекул и в обеспечении взаимодействия биомолекул между собой. Атом водорода, входящий в состав одной
молекулы M1A − H , образует вторую, обычно более слабую связь с ато-
⎧⎪⎛ σ ⎞12 ⎛ σ ⎞6 ⎫⎪
V ( R) = 4ε ⎨⎜ ⎟ − ⎜ ⎟ ⎬ .
⎝ R ⎠ ⎭⎪
⎪⎩⎝ R ⎠
мом B другой молекулы BM 2 , в результате чего обе молекулы объеди-
100
101
няются в комплекс M1A − H " BM 2 через так называемый водородный
мостик − A − H " B − (рисунок 62), в записи которого водородная связь
изображается пунктиром. Обычно RHB > rA − H .
А
H
B
r
RHB
R
а
б
Рисунок 62 – Схема образования водородной связи: а – водородный мостик
− A − H " B − , б – пример образования водородной связи между аминокислотами
Наибольшей стабильностью H -связь обладает при линейном расположении атомов − A − H " B − . Атомы A ( F, O, N, Cl ) и B в водородном
мостике обладают высокой электроотрицательностью. Атом B обычно
имеет неподеленную электронную пару. В процессе образования H -связи
электронный заряд с атома H "перетекает" на электроотрицательный
атом A , тем самым высвобождая s -орбиталь водорода ("оголяя" протон)
который эффективно притягивает электронное облако неподеленной
электронной пары атома B . Таким образом, механизм образования водородной связи двух электроотрицательных атомов через протон весьма
близок к донорно-акцепторному.
Современные квантовомеханические расчеты, выполненные с учетом
всех атомов молекулы, показали, что при образовании H -связи изменяется распределение электронной плотности не только у атомов, непосредственно образующих H -мостик, но и на всех остальных атомах, причем
полярность молекул возрастает, что усиливает их взаимодействие. Молекулы таких жидкостей, как HF, вода и спирты, могут при образовании
водородных связей выступать как акцепторы и доноры электронного заряда одновременно. В результате этого происходит ассоциация молекул –
образование димеров, тримеров, тетрамеров и т.д., пока тепловое движение не разрушит образовавшиеся кольца или цепочки молекул.
102
Наряду с межмолекулярной H -связью осуществляется и внутримолекулярная водородная связь. Образование её возможно при одновременном наличии в молекуле донорной группы A − H и акцепторной
группы, содержащей атом B .
Водородные связи функционально напоминают застежку-"липучку";
они, как многоразовый крепеж, могут соединяться и разъединятся в зависимости от необходимости.
Водородные связи слабее ковалентных и не так жестко ориентированы, но их энергия несколько больше, чем характерная термическая энергия при физиологических температурах, поэтому они являются
стабильными для биологических объектов. Поскольку они слабее ковалентных связей, их легче разорвать.
Поверхностное натяжение воды, приводящее к формированию дождевых капель, является физическим проявлением сильных водородных
связей между молекулами воды, в то же время в том, что вода является
жидкостью при комнатных температурах, проявляется та легкость, с которой образуются и рвутся водородные связи. Система водородных связей определяет уникальные свойства воды – самого распространенного
соединения в живых организмах (рисунок 63).
Вода заполняет клетки и межклеточные пространства и представляет собой ту среду, в которой осуществляются диффузия веществ,
химические реакции и взаимодействия макромолекул (белков и нуклеиновых кислот) друг с другом.
Кроме того, вода сама непосредственно участвует во многих химических реакциях клетки. Два свойства воды: способность образовывать
водородные связи и обратимая ионизация – оказываются весьма существенными для протекания внутриклеточных процессов.
Атомы кислорода и водорода обладают разным сродством к электрону (электроотрицательностью), и, хотя молекула воды в целом электрически нейтральна, на кислороде локализуется частичный отрицательный (2δ− ) , а на атомах водорода – частично положительный (δ+ )
заряды. Два электроотрицательных атома связываются через атом водорода, образуя водородную связь.
103
цитозин (G≡C), которые в честь Джеймса Уотсона и Френсиса Крика, открывших структуру ДНК, называют "уотсон-криковские пары".
Водородные связи намного слабее ковалентных. Энергия водородных связей в жидкой воде (т.е. энергия, необходимая для разрушения одной связи) составляет примерно 18,8 кДж/моль, тогда как энергия
ковалентных связей Н–О в молекулах воды примерно в 25 раз больше.
а
б
в
Рисунок 64 – Внутримолекулярные водородные связи в белках и нуклеиновых
кислотах: а – сила связи наибольшая при линейном расположении атомов, б – водородные связи между полипептидными цепями белков, в – азотистые основания цитозин и гуанин в ДНК спариваются, образуя водородные мостики
Молекулы в жидкой воде находятся в непрерывном тепловом движении, поэтому образующиеся водородные связи постоянно и быстро
разрываются и вновь восстанавливаются. Среднее время жизни водород-
Белки и нуклеиновые кислоты содержат большое число внутримолекулярных водородных связей, которые играют важную роль в организации структуры и функционировании этих макромолекул (рисунок 64).
В белках водородные связи между пептидными группами формируют вторичные структуры.
В нуклеиновых кислотах именно водородные связи обеспечивают
спаривание комплементарных нуклеиновых оснований. В ДНК такими
стандартными парами являются пары аденин-тимин (А=Т) и гуанин-
ной связи при комнатной температуре не превышает 1,5×10–9 с. Каждая
молекула воды может образовывать водородные связи с четырьмя соседними молекулами, однако при комнатной температуре каждая молекула
воды образует водородные связи в среднем с 3,4 других молекул. Любые
молекулы, между которыми возможны водородные связи, могут образовывать такие же связи с молекулами воды. Из-за такой конкуренции с молекулами воды водородные связи, образуемые между двумя молекулами в
водном растворе, относительно слабы (рисунок 65).
Аномально высокие (по сравнению с большинством других жидкостей) удельная теплоемкость и теплота испарения воды является следствием высокого межмолекулярного сцепления в воде, обусловленного
образованием водородных связей. Эти особенности воды важны для поддержания постоянства внутренней температуры живыми организмами.
104
105
Рисунок 63 – Молекулярные свойства воды: а – пространственное расположение химических связей; б – схема водородной связи; в – структура связей в жидкой
воде; г – длина связей; д – нерастворимость в воде гидрофобных (в частности, углеводородов) молекул; е – гидратация ионов и гидрофильных молекул
При изменении температуры внешней среды в клетке происходит поглощение или выделение тепла благодаря разрыву или новообразованию водородных связей между молекулами воды. Таким образом, колебания
температуры внутри клетки, несмотря на её резкие изменения во внешней
среде, ослабляются – вода выступает в роли термостата. Благодаря высокой теплоте испарения воды организмы могут эффективно защищаться
от перегрева, поскольку на испарение 1 г воды с поверхности листа или в
виде пота с поверхности кожи расходуется 2,26 кДж тепловой энергии.
дальнодействующими. Электростатические силы используются как на
малых расстояниях для связывания атомных групп, так и на больших расстояниях, для притяжения или отталкивания необходимых молекул. Они
не являются направленными и действуют симметрично во всех направлениях от заряженного центра.
а
Рисунок 65 – Эволюция водородных связей в водном растворе
Полярный характер молекулы воды делает её значительно лучшим
растворителем, чем большинство других общеизвестных жидкостей.
В воде растворяются очень многие вещества, причем растворимость некоторых веществ определяется способностью воды образовывать водородные связи с гидроксильными и карбоксильными группами других молекул.
Электростатические силы. Электростатические силы обеспечивают взаимодействие между полностью или частично заряженными функциональными группами (рисунок 66).
Электростатическое взаимодействие между атомами, имеющими
нескомпенсированный электрический заряд, играет важную роль в
стабилизации биомолекул. Электростатические взаимодействия являются
106
б
Рисунок 66 – Электростатическое взаимодействие в биомолекулах: а – вверху –
лизин и глутаминовая кислота притягиваются, внизу – лизин и аргинин отталкиваются; б – схема фермента супероксид-дисмутаза, обеспечивающего детоксикацию: 1 –
ионы меди и цинка в активном центре фермента связывают и химически модифицируют супероксиды (перекиси); 2 – гистидины, которые удерживают ионы металлов в
ферменте
Выделим некоторые виды электростатических взаимодействий, общих для всех биообъектов.
(1) Прежде всего, это солевые мостики, образующиеся между органическими группами, несущими формальный заряд (в этом они подобны
ионным связям в кристаллах неорганических солей). Солевые мостики
характерны для поверхностей белков, где они служат для стабилизации
структуры. Когда требуется дополнительные силы, в белки встраиваются
заряженные сульфатные или фосфатные группы.
(2) Во-вторых, белки часто включают в себя ионы металлов – от
легкого магния до тяжелых железа и кобальта – для стабилизации струк107
туры или для выполнения специфических химических функций (рисунок 66(б)).
Описанные выше силы легко понять, представив себе молекулу как
комбинацию атомов – следует просто просуммировать такие парные
межатомные вклады ковалентных связей, водородных связей, ван-дерваальсовых и электростатических сил, чтобы предсказать поведение биомолекулы.
При помещении в воду, однако, картина оказывается гораздо более
сложной. Возникающий в воде гидрофобный эффект определяет свойства биомолекул и взаимодействие между ними. Молекулы воды интенсивно взаимодействуют между собой, образуя водородные связи. Жидкая
вода образуется перемещающимися молекулами воды, которые постоянно
формируют и переформировывают водородные связи с соседними молекулами. Стабильность водного раствора определяется комбинацией эн-
тальпий ван-дер-ваальсовых и водородных связей и энтропии, которая
стремится увеличить число беспорядочно ориентированных молекул.
Водородные связи между молекулами воды энтальпически выгодны,
поскольку при этом образуется много стабилизирующих взаимодействий.
Они также энтропически выгодны, поскольку каждая молекула воды имеет неограниченное количество возможностей для взаимодействия со всеми остальными молекулами воды, причем все эти взаимодействия имеют
одинаковую энергию.
Любое воздействие, которое будет нарушать этот процесс должно
обеспечить эквивалентное количество энтальпии во взаимодействиях с
таким же количеством энтропического разнообразия, в противном случае
оно будет энергетически невыгодным.
Однако биомакромолекулы собраны главным образом из углерода,
который очень слабо взаимодействует с окружающей водой. Когда углеводородные молекулы помещаются в воду, молекулы воды, окружающие
углеводороды, теряют свою способность свободно формировать и перестраивать водородные связи с соседними молекулами воды.
С одной стороны, они, взаимодействуя с углеводородами и образуя
с ними слабые ван-дер-ваальсовые связи, проигрывают энергетически,
поскольку они теряют возможность образовывать водородные связи с теми молекулами воды, на чьем месте расположилась молекула углеводорода.
С другой стороны, молекулы воды, примыкающие к углеводороду,
стремятся максимально использовать оставшиеся возможные взаимодействия с соседними молекулами воды, а это ограничивает их способность к
свободному перемещению по водному раствору. Молекулы воды формируют клатратную конструкцию вокруг каждого углеводородного включения, что снижает энтропию, а значит, энергетически невыгодно
(рисунок 67).
Если теперь собрать эти углеводородные включения и сгруппировать их в одном месте (рисунок 67(б)), то ситуация улучшится. Общая
площадь поверхности углеводородной фазы, которая доступна молекулам
воды будет уменьшаться по мере ассоциирования углеводородных моле-
108
109
Часто ионы должны быть помещены в специфические химические
"контейнеры", которые обеспечивают необходимую ориентацию иона и
использование нужного электронного состояния иона.
Интенсивность электростатических взаимодействий снижается за
счет диэлектрического эффекта, который зависит от того, какие атомы
расположены между заряженными атомами и вокруг них.
Вода является сильным диэлектриком, сильно уменьшая электростатическое взаимодействие ионов. Белки, напротив, являются слабыми
диэлектриками.
Молекулы воды являются диполями – атом кислорода несет избыточный отрицательный заряд, а два атома водорода – избыточный положительный. Когда ионы помещаются в водный раствор, окружающие
молекулы воды разворачиваются. Это снижает воздействие данного иона
на другие ионы снижая силу электростатических взаимодействий в 81 раз.
Атомы в белках более фиксированы и не могут совершать такую динамическую реорганизацию.
5.3. ГИДРОФОБНЫЙ ЭФФЕКТ
кул. При этом множество молекул воды будут "освобождены" из клатратных корзинок в раствор. Углеводороды в свою очередь будут увеличивать
число дисперсионных связей между собой.
Все это снижает общую энергию системы и проявляется как гидрофобный эффект, собирающий углеводороды в единую фазу с возможно
большим числом освобожденных в раствор молекул воды. На молекулярном уровне гидрофобный эффект является движущей силой большинства
процессов самосборки в биомолекулярной механике.
а не какого-либо внутреннего взаимодействия между углеводородными
молекулами.
Рассмотрим подробнее молекулы белков, для которых гидрофобный
эффект является определяющим фактором сворачивания в функциональную третичную форму. Аминокислотные остатки, входящие в состав полипептидной цепи, условно разделяют на гидрофобные и гидрофильные.
В таблице 7 приведено изменение свободной энергии при перенесении
аминокислот из этилового спирта в воду.
Таблица 7 – Гидрофобность аминокислотных остатков – значение
ΔG (кДж/моль) при перенесении аминокислот из этанола в воду
Гидрофобные остатки
Trp
12,51
Ile
Tyr
Phe
Pro
Leu
12,40 12,00 11,09 10,85 10,10
Val
Lys
His
Met
7,06
6,27
5,85
5,45
Гидрофильные остатки
а
б
Рисунок 67 – Гидрофобное взаимодействие: а – неагрегированное, энергетически невыгодное состояние, водное окружение более упорядочено, энтропия ниже;
б – агрегированное, энергетически выгодное состояние, водное окружение менее упорядочено, энтропия выше; 1 – неполярное вещество; 2 – упорядоченные молекулы воды; 3 – молекулы воды, освобожденные в объем раствора
Иногда более удобно представлять себе гидрофобный эффект как
определенные гидрофобные взаимодействия, которые стабилизируют ассоциат углеводородных молекул.
Нужно только всегда помнить, что такие стабилизирующие взаимодействия являются следствием освобождения в раствор молекул воды,
110
Ala
Arg
Cys
Glu
Asp
Thr
Ser
Gly
Asn
Gln
3,05
3,05
2,71
2,3
2,26
1,84
0,17
0,00
–0,44
–0,42
Гибкая макромолекула белка в воде сворачивается в глобулу, поскольку термодинамически выгоден максимальный контакт полярных остатков с водным окружением, и, наоборот, минимальный контакт
неполярных остатков с водой.
Поскольку минимальной поверхностью при данном объеме обладает шар, то такое "стремление" неполярных радикалов образовать внутри
белковой молекулы некоторое подобие углеводородной капли, по форме
близкой к шарообразной, а гидрофильных и заряженных групп – сосредоточиться на поверхности белковой молекулы, приводит к формированию
компактной частицы – глобулы с гидрофобным ядром и гидрофильной
поверхностью. Зная общее число аминокислотных остатков в белке и отношение числа полярных аминокислот к неполярным, можно предсказать
форму глобулы (рисунок 68).
111
На рисунке 68 приведена теоретическая кривая (кривая Фишера)
значений b в зависимости от объема глобулы V , а также экспериментальные значения V и b для ряда белков. Экспериментальные точки располагаются вблизи кривой Фишера, однако, как правило, выше нее.
Глобула может быть сферической лишь при b = bs .
Если b > bs , т.е. полярных остатков в белке больше, чем необходимо
для того, чтобы покрыть гидрофобное ядро гидрофильным слоем, то глобула вытягивается в виде эллипсоида и имеет бóльшую площадь, чем в
случае сферы. На рисунке 68 такие белки обозначены кружками. Если b
значительно больше bs , то возникает фибриллярная структура (крестики
на рисунке 68).
Напротив, при b < bs гидрофильные остатки не полностью закрывают гидрофобные. Гидрофобные взаимодействия между такими участками ведут к агрегации белков и возникновению надмолекулярных
структур (треугольники на рисунке 68).
Таким образом, белки, для которых значения b
Рисунок 68 – Модель белка: а – форма белковой молекулы в зависимости от параметра b; б – кривая Фишера. Изменение V при агрегации обозначено стрелками
Если все остатки занимают одинаковые объемы, то в этом случае
отношение b числа гидрофильных остатков к гидрофобным равно для
сферической глобулы
bs =
Число гидрофильных аминокислот
3d
=
,
Число гидрофобных аминокислот (r0 − d )3
где r0 – радиус глобулы; d – толщина внешнего гидрофильного слоя, рав-
1) лежат выше кривой Фишера – представляют собой эллипсоиды и фибриллы,
2) лежат на кривой – представляют собой глобулы,
3) под кривой располагаются белки, образующие надмолекулярные четвертичные структуры.
Формирование гидрофобного ядра в глобулярных белках имеет
принципиальное значение для их функционирования. Благодаря гидрофобным взаимодействиям белки при большой молекулярной массе обладают сравнительно компактной структурой, при этом компактно
упакованная глобула находится в одной, наиболее устойчивой конформации.
Кроме гидрофобных сил глобулярную структуру белковой молекулы стабилизируют, конечно же, и система внутрибелковых нековалентных связей – ван-дер-ваальсовые силы, электростатические взаимодей-
ная ~0,4 нм.
112
113
ствия и водородные связи, и ковалентно связанные дисульфидные мостики между остатками цистеинов.
На рисунке 69 схематически представлены перечисленные выше
взаимодействия, стабилизирующие пространственную структуру белков.
изменения внутри белка, определяя жесткость конструкции и общий характер потенциальных барьеров для внутренних движений частей нативной структуры.
В то же время гидрофобные взаимодействия между боковыми
группами на отдельных участках основной цепи играют решающую роль
в процессах сворачивания глобулы из первичной аминокислотной
последовательности и в определении её общей формы.
В обоих случаях вода как растворитель имеет огромное значение,
облегчая полярные взаимодействия за счет образования водородных связей, как на поверхности, так и внутри макромолекулы.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
Рисунок 69 – Связи и взаимодействия, стабилизирующие пространственную
структуру белков: I – ионная; II – водородная; III – дисульфидная; IV – гидрофобные
взаимодействия
Таким образом, характер нативной (природной) конформации определяется не каким-либо одним эффектом, а представляет собой результат совместного тонко сбалансированного действия целого ряда
энергетических и энтропийных факторов.
Водородные связи, образованные между полярными группами и водой, и внутри глобулы, – главный фактор в обеспечении стабильности отдельных областей белка. Они ограничивают локальные конформационные
114
1. Перечислите нековалентные взаимодействия, стабилизирующие
функциональную структуру ферментов.
2. От чего зависит энергия диполь-дипольного взаимодействия?
3. От чего зависит энергия индукционного взаимодействия?
4. От чего зависит энергия дисперсионного взаимодействия?
5. Каковы особенности водородной связи по отношению к остальным видам нековалентных взаимодействий?
6. Где используются водородные связи при формировании функциональной структуры белков и ДНК?
7. Какие молекулярные свойства воды определяют её биологическую значимость?
8. Каковы особенности электростатических взаимодействий по отношению к остальным видам нековалентных взаимодействий?
9. Что такое гидрофобный эффект?
10. В чем отличие в поведении гидрофобных и гидрофильных аминокислот во время белкового фолдинга?
11. Что описывает кривая Фишера?
12. Каково должно быть соотношение гидрофильных аминокислот к
гидрофобным аминокислотам в белке, чтобы происходило спонтанное формирование фибриллярных белковых структур?
115
цию от такой же, но некаталитической, реакции, которая протекает в
водном растворе без участия катализаторов (рисунок 70).
РАЗДЕЛ II
МЕХАНИЗМЫ ФЕРМЕНТАТИВНЫХ ПРОЦЕССОВ
Рисунок 70 – Некаталитическая реакция (в отсутствие фермента)
При ферментативных превращениях происходит множество взаимосвязанных процессов и явлений на пути превращения субстрата в продукт
биохимической реакции под действием фермента. В молекулярном смысле под механизмом понимают молекулярные события, стимулирующие
превращение одних молекул в другие. Реальные механизмы ферментативных процессов, объясняющие работу конкретных ферментов, могут
различаться чрезвычайно, но все ферментативные реакции имеют ряд
общих особенностей, изложению которых и посвящен данный раздел
курса.
Вещества A и В в растворе окружены оболочкой из молекул воды
(гидратной оболочкой) и под действием теплового движения перемещаются случайным образом. Они могут вступать в реакцию друг с другом
только в том случае, когда сталкиваются в благоприятной ориентации,
что маловероятно и происходит редко. Для образования продуктов C и D
комплекс AВ, возникший в результате соударения молекул, должен образовать переходное состояние, для чего требуется, как правило, значительная энергия активации Ea . Поскольку получить эту энергию может
Подробно специфика и кинетика мультисубстратных ферментативных реакций изложена в пособии [4], и будет рассмотрена в третьем разделе курса, сейчас же нас будут интересовать исключительно
специфические особенности, которые отличают ферментативную реак-
только небольшая часть комплексов AВ, достижение переходного состояния – ещё более редкий случай, чем возникновение комплекса.
В растворе большая часть энергии активации расходуется на преодоление гидратных оболочек между A и В, в результате, в отсутствие
катализатора, образование продуктов происходит крайне редко и скорость
реакции – незначительна, даже когда реакция термодинамически допустима, т. е. ΔG < 0 .
Участие ферментов существенно повышает "эффективность" образования переходного состояния (рисунок 71). Ферменты специфически
связывают реагенты (свои субстраты) в активном центре.
Активным центром называется область молекулы фермента, в которой происходит связывание и превращение субстрата.
Связывание субстратов в активном центре приводит к тому, что
субстраты ориентируются таким образом, что приобретают оптимальное
положение для образования переходного состояния (рисунок 71(1–3)).
116
117
Глава 6
БИОКАТАЛИЗ
6.1. СПЕЦИФИКА ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
Рассмотрим бисубстратную ферментативную реакцию фермента E
с субстратами A и B с образованием продуктов C и D
E + A + B → EAB → ECD → E + C + D .
Сближение и необходимая ориентации реагентов значительно повышают вероятность образования продуктивного комплекса AB. Кроме
того, связывание субстрата в активном центре приводит к удалению гидратной оболочки субстрата. В результате удаления молекул воды в активном центре фермента во время катализа создаются совершенно другие
условия, чем в растворе (рисунок 71(3–5)). Таким образом, переходное
состояние в случае ферментативной реакции требует меньшей энергии
активации.
валентно присоединяются к аминокислотам фермента. Это явление называют ковалентным катализом.
Таким образом, отличие ферментативных реакций от неферментативных заключается в том, что в ходе ферментативных реакций
образуется фермент-субстратный комплекс, в котором происходит:
1)
2)
3)
4)
сближение и ориентация субстратов,
исключение из реакционной области молекул воды,
стабилизация переходного состояния,
перенос группы атомов.
Все эти события и действия происходят в активном центре фермента. В нем специфические аминокислоты располагаются в стратегически важных пространственных положениях, они идеально позиционированы для стабилизации переходного состояния молекулы субстрата.
Для примера на рисунке 72 в левой части приведена схема ферментсубстратного комплекса: цитохром Р450–камфора. В правой части рисунка 72 показана схема активного центра этого комплекса.
Рисунок 71 – Схема ферментативной реакции
Еще одним важным фактором является стабилизация переходного
состояния вследствие взаимодействия между аминокислотными остатками белка и субстратом (рисунок 71(4)).
Кроме того, многие ферменты во время катализа переносят специфические группы атомов с субстрата или на субстрат. Особенно часто
осуществляется перенос протонов. Этот ферментативный кислотноосновной катализ значительно более эффективен, чем обмен протонов с
кислотами и основаниями в растворе. Часто функциональные группы ко118
Рисунок 72 – Фермент-субстратный комплекс цитохром Р450–камфора (слева) и
схема активного центра этого комплекса (правая часть рисунка). Цитохромом Р450
называют группу гемсодержащих монооксигеназ
119
Активный центр формируется из фрагментов полипептидной цепи,
в том числе из отдельных аминокислот, содержащих разнообразные
функциональные группы. Некоторые из них принимают участие в сорбции субстрата на ферменте, другие – катализируют его химическое превращение. К каталитически активным радикалам белка относятся
нуклеофильные группы (имидазол гистидина, гидроксильная группа серина или тирозина, тиольная группа цистеина, ε-аминогруппа лизина, ионизированные карбоксилы аспарагиновой и глутаминовой кислот и др.) и
электрофилы (ион имидазола, неионизованные карбоксильные группы,
ионы металлов и т. п.).
В первичной структуре молекулы фермента группы активного центра обычно удалены друг от друга (рисунок 73).
тированы) в сближенном состоянии, удобном для "одновременного" их
взаимодействия с сорбированной молекулой субстрата.
В формировании активного центра принимают участие также молекулы воды, входящие в гидратационные слои, а в ряде случаев ионы металлов, связанные с белком, и органические кофакторы. Определенную
жесткость такой конструкции придают α-спирали, β-структуры и дисульфидные мостики.
Ферменты осуществляют химические трансформации, прокладывая
путь реакционной системе в необходимом направлении снижая препятствующие барьеры.
Протекание химической реакции можно образно сравнить с процессом "ломания" карандаша. Вначале карандаш прямой и твердый. Когда
мы начинаем его сгибать, карандаш сопротивляется, в нем нарастают напряжения. Наконец он ломается, и у нас в руках остаются два прямых и
твердых куска карандаша. Химическая реакция разрыва связи совершенно
аналогична. Когда мы расщепляем молекулу на две части, мы должны
приложить силу, чтобы ослабить связь.
И исходное состояние, и конечные фрагменты молекулы являются
стабильными, но промежуточное состояние, в котором химические связи
напряжены и растянуты, является нестабильным и энергетически невыгодным.
Ферменты снижают величину энергетического барьера в промежуточном состоянии,
(1) облегчая его формирование из исходного состояния субстрата,
(2) облегчая преобразование субстрата именно в необходимые продукты.
Рисунок 73 – Схема фермента лизоцим (ЕС 3.2.1.17). Вверху изображены компоненты активного центра; внизу – номера их положений в первичной структуре полипептидной цепи
Однако в третичной структуре аминокислотные остатки, принимающие участие в катализе, определенным образом фиксированы (ориен-
Так в примере с карандашом, если ногтем процарапать глубокую
поперечную бороздку на карандаше, то карандаш ломается гораздо легче,
причем именно в том месте, которое мы отметили. Мы "катализировали"
реакцию "слома" карандаша, "стабилизировав" ногтем промежуточное состояние (царапина), и облегчив начало "разлома" в нужном месте.
120
121
Совершенно аналогично ферменты создают такое молекулярное окружение, в котором переходное состояние стабилизируется и снижается
барьер (облегчается переход) к формированию продуктов реакции.
Следовательно, структурные особенности поверхностного слоя белковых глобул позволяют сосредоточить в активном центре большое
число различных по химической природе функциональных групп, способных не только сорбировать субстрат на ферменте, но и стимулировать
химическую трансформацию.
Часто активный центр помещается в "стандартном дефекте" макромолекулы белка – в стандартно расположенной (т. е. определяемой мотивом укладки цепи, а не боковыми группами) вмятине в архитектуре
белковой глобулы. Такая вмятина автоматически способствует окружению субстрата одновременно многими боковыми цепями белка.
Столь же обычным местом активного центра является место стыка
доменов.
Такое положение активного центра обусловливает формирование
особой среды, отличающейся от той, что окружает молекулы в растворе
(клетке). Среда активного центра отличается, как правило, сильно развитой микрогетерогенностью. Поверхностный слой белковой глобулы характеризуется повышенной микровязкостью.
Эффекты повышенной микровязкости особенно сильно развиты в
области активного центра. Здесь полипептидные цепи белка расположены
настолько жестко, что затрудняют не только поступательную диффузию в
глобулу, но также и вращательное движение связанной молекулы.
Механизмы, которые играют главную роль при связывании субстрата в активном центре фермента и образовании комплекса ферментсубстрат в воде:
1) образование ковалентных связей;
2) гидрофобные взаимодействия между неполярными (углеводородными) фрагментами субстратной молекулы и дегидратированными (хотя бы частично) областями поверхностного
слоя глобулы;
122
3) электростатические взаимодействия между заряженными
группами субстрата и ионизованными аминокислотными остатками полипептидных цепей;
4) образование водородных связей.
Исторически первой моделью, учитывающей образование ферментсубстратного комплекса ES , в которой непосредственное взаимодействие
фермента с субстратом обеспечивалось тождественностью формы субстрата S и вмятины в архитектуре фермента E , была модель "ключзамок" Эмиля Фишера (1890 г.) (рисунок 74(а)). Ниже (п. 7.2) мы рассмотрим механизм сближения и ориентации, который соответствует модели "ключ-замок" Эмиля Фишера.
а
б
Рисунок 74 – Модели фермент-субстратного связывания: а – модель "ключзамок" Фишера; б – Модель "рука-перчатка" Кошланда
Позже, в 1958 году, Даниэль Кошланд предложил модель "рукаперчатка" (рисунок 74(б)), которая учитывала тот факт, что связывание
субстрата S на ферменте E само по себе должно приводить к существенному изменению пространственной организации фермента.
Субстрат связывается с активным центром двумя или большим числом точек. Образованию весьма прочных "многоточечных" (хелатных)
комплексов способствует то, что полипептидные цепи белка и особенно
боковые группы аминокислотных остатков, находящихся в поверхностном слое, не зафиксированы слишком жестко и обладают определенной
123
подвижностью (гибкостью). В результате обеспечивается возможность
пространственной настройки отдельных сорбционных участков глобулы
на соответствующие (связываемые ими) фрагменты сорбируемой молекулы.
Сорбционный участок глобулы, способен принять конфигурацию,
отличную от равновесной (т. е. термодинамически устойчивой в отсутствие субстрата), чтобы обеспечить наибольший контакт фермента с
субстратом. В результате такого электронно-конформационного взаимодействия фермента с субстратом и формируется активный центр, в котором фермент и субстрат "подстроились" друг к другу. Такой механизм
называется механизмом индуцированного соответствия (п. 7.2).
6.2. ФОСФОРИЛИРОВАНИЕ БЕЛКОВ ФЕРМЕНТОМ
ПРОТЕИН-КИНАЗА А
В качестве примера рассмотрим работу фермента протеин-киназа А,
который осуществляет реакцию фосфорилирования многих белков.
Неактивная протеин-киназа А (ПКА) существует в цитоплазме
клетки в виде тетрамерного белка, состоящего из двух каталитических (С)
и двух регуляторных (R) доменов (рисунок 75).
Активация ("включение") протеин-киназы А осуществляется связыванием с регуляторными субъединицами специфического лиганда –
сигнальной молекулы циклического аденозинмонофосфата, цАМФ (рисунок 76).
Циклический аденозинмонофосфат образуется из АТФ в процессе
реакции, катализируемой ферментом аденилатциклазой (ЕС 4.6.1.1), и
выполняет роль медиатора внеклеточных сигналов в клетке животных.
В нашем случае цАМФ активирует протеин-киназу А.
Связывание цАМФ с регуляторным доменом индуцирует конформационное изменение в псевдосубстратной последовательности, сродство каталитических доменов к регуляторным резко снижается и каталитические домены освобождаются.
Таким образом, при росте концентрации цАМФ (в ответ на внешнее
событие) киназный тетрамер диссоциирует на две мономерные каталитические субъединицы и одну димерную регуляторную субъединицу (рисунок 75).
Когда внешний сигнал исчезает и уровень цАМФ снижается, активность протеин-киназы А "выключается", поскольку восстанавливаются
инактивные тетрамеры.
Рисунок 75 – Активация протеин-киназы А (ПКА), индуцированная лигандом
Каждый регуляторный домен имеет псевдосубстратную последовательность аминокислот, с которой связываются каталитические домены, иными словами регуляторные домены блокируют работу
каталитических доменов, ингибируют их активность.
Протеин-киназа А, как и остальные протеин-киназы, переносит
фосфатную группу с АТФ на оксиаминокислоты тирозин, серин или тре-
124
125
Рисунок 76 – Циклический аденозин монофосфат (цАМФ)
онин (рисунки 27, 30, 31), тем самым изменяя активность необходимых
белков (фосфорилирует их), в том числе и в ответ на внешнее воздействие.
Поэтому протеин-киназа А является мультисубстратным (бисубстратным) ферментом. Субстратами протеин-киназы А являются (1) АТФ
и (2) фосфорилируемый белок. Для реализации фосфорилирования должен образоваться тройной комплекс фермента с двумя субстратами.
Все протеин-киназы принадлежат к одному белковому семейству,
поэтому структура активного центра и механизм фосфорилирования у них
подобны.
Активный центр протеин-киназы А расположен на каталитической
субъединице, построенной из 240 аминокислот, которая называется киназное ядро (kinase core) (рисунок 77).
а
б
Рисунок 77 – Протеин-киназа А: а – схема киназного ядра; б – конформации
киназного ядра
Киназное ядро, состоящее из двух доменов – большого и малого,
разделенных глубокой щелью ("карманом"), связывает АТФ и белоксубстрат в этой щели (стандартный дефект) и активирует перенос фосфатной группы с АТФ на белок-субстрат.
126
Активный центр формируют аминокислотные остатки обеих доменов киназного ядра. Адениновое кольцо АТФ точно укладывается в основание щели между двумя доменами и фиксируется там "глициновой
крышкой", которая образована последовательностью Gly–X–Gly–X–X–
Gly–X–Val (X – любая аминокислота).
АТФ является общим субстратом для всех протеин-киназ, однако
каждая протеин-киназа распознает специфический белок-субстрат по специфической для него последовательности аминокислот. Для протеинкиназы А такая последовательность: Arg–Arg–X–Ser–Y, где Х – любая
аминокислота, Y – гидрофобная аминокислота.
Каталитическое ядро протеин-киназы А может принимать одну из
двух конформаций – "открытый карман" или "закрытый карман".
В "открытой" конформации субстраты могут "погрузиться" в карман и
связаться с активным центром. Связывание субстратов стимулирует конформационный переход молекулы фермента, карман закрывается глициновой крышкой и активируется перенос фосфатной группы с АТФ на
белок-субстрат. Это пример механизма "индуцированного соответствия"
(induced fit) фермента и субстрата, когда топология активного центра
фермента "подгоняется" под топологию субстрата.
Молекулы АДФ и фосфорилированного белка-субстрата теряют
сродство к ферменту после фосфорилирования, фермент претерпевает
конформационный переход в "открытую" форму, "поднимается" глициновая крышка, карман открывается, и модифицированные субстраты выходят из него.
Таким образом, в каталитическом цикле фосфорилирования белков
ферментом протеин-киназа А происходят все четыре процесса (стр. 119),
которые являются специфическими для ферментативных реакций.
6.3. ОСОБЕННОСТИ ФУНКЦИОНИРОВАНИЯ ФЕРМЕНТОВ
В ферментах реализовано множество различных приемов, позволяющих повысить каталитическую активность. На первый взгляд кажется,
что каждый активный центр должен быть устроен по-своему как результат эволюционного отбора.
127
Однако несколько общих функциональных принципов используются в конструкции активного центра большинства ферментов:
(1) снижение энтропии,
(2) химическая стабилизация переходного состояния (‡),
(3) использование специализированных химических инструментов.
структурой", единственное назначение которой – это точно расположить в
пространстве те несколько ключевых аминокислот, которые и осуществляют химическую трансформацию.
Триозофосфатизомераза катализирует реакцию изомеризации, удаляя два атома водорода от дигидроксиацетон-фосфата, а затем добавляя
эти же атомы в другие позиции в молекуле, образуя глицеральдегид-3фосфат.
Рассмотрим, например (рисунок 78), фермент триозофосфатизомеразу (ЕС 5.3.1.1).
Рисунок 78 – Фермент триозофосфатизомераза: 1 – молекула субстрата в активном центре фермента
Триозофосфатизомераза является ферментом, имеющим диффузионные ограничения скорости протекания реакции – это означает, что фермент производит химические трансформации с большей скоростью, чем
скорость диффузии субстратов к ферменту. Триозофосфатизомераза использует все приемы ферментативного катализа. Сам фермент представляет собой димер, состоящий из двух идентичных субъединиц, каждая из
которых имеет свой активный центр, в котором связывается молекула
субстрата.
Молекула фермента намного больше молекулы субстрата. Практически весь объем молекулы фермента является той необходимой "инфра128
Реакция осуществляется в два этапа (рисунок 79).
На первом этапе, изображенном в верхней части рисунка 79, глутаминовая кислота принимает на себя один из атомов водорода от субстрата, а гистидин добавляет к молекуле субстрата другой атом водорода.
На втором этапе, изображенном в нижней части рисунка 79, глутаминовая кислота присоединяет этот "лишний" атом водорода к субстрату,
но уже в другой позиции, а гистидин "отнимает" себе недостающий ему
атом водорода от субстрата, но не оттуда, куда он добавлял водород, а из
другой позиции.
Заметим, что фермент в итоге оказался в том же состоянии, что и до
начала реакции – со свободной глутаминовой кислотой и с атомом водорода, связанным с гистидином (хотя этот атом водорода уже не "тот самый", который был у гистидина изначально).
Таким образом, по завершении реакции, молекула фермента готова
к следующему преобразованию субстрата в продукт, когда диффузия
"доставит" субстрат к ферменту.
129
Фермент ускоряет химическую реакцию, стабилизируя переходное
состояние в обоих этапах.
Переходное состояние первого этапа показано на рисунке 80(б).
Глутаминовая кислота уже приняла на себя атом водорода, а гистидин
ещё не отдал свой водород субстрату. В результате субстрат оказался избыточно отрицательно заряженным (энергетически невыгодно), но этот
избыточный отрицательный заряд, сконцентрированный на одном из атомов кислорода, стабилизируется расположенным рядом положительно
заряженным лизином.
а
б
Рисунок 79 – Схема реакции изомеризации, катализируемая ферментом триозофосфатизомераза
Рисунок 80 – Схемы: а – ориентации субстрата в ферменте; б – стабилизации
переходного состояния
Фосфатная группа субстрата окружена набором аминокислот фермента, которые расположены в пространстве так, что они образуют "карман" в теле фермента (рисунок 80(а)).
Фосфатная группа молекулы субстрата точно позиционируется в
этом кармане благодаря системе водородных связей с окружающими
аминокислотами (показаны пунктиром на рисунке 80), при этом область
изомеризации оптимальным образом располагается по отношению к глутаминовой кислоте и гистидину активного центра фермента.
Уменьшение ферментами энтропии химических реакций. Ферменты ускоряют химические реакции, собирая все необходимые компоненты в нужном месте в нужное время.
Энтропия препятствует протеканию химических реакций, снижая
вероятность того, что реагирующие молекулы встретят друг друга и провзаимодействуют необходимым образом.
130
131
В бимолекулярных реакциях энтропия снижает вероятность
встречи обеих реагирующих молекул.
В реакциях требующих однозначной ориентации реагентов для преобразования химических связей, энтропия снижает вероятность выбора
такой строгой ориентации из большого числа других взаимных ориентаций реагентов.
Ферменты как раз и являются теми молекулярными приспособлениями, которые минимизируют энтропийный фактор, оптимально позиционируя реагенты в пространстве и стимулируя перенос функциональных групп в нужном направлении.
Активные центры топологически и химически соответствуют молекулам субстратов (комплементарны), образуя гидрофобные, электростатические, водородные и (редко) ковалентные связи субстрата с
ферментом. Фермент обычно контактирует с большей частью молекулы
субстрата, а некоторые ферменты полностью закрывают активный центр
со связанным субстратом, используя белковые петли и домены в качестве
"ворот" и "крышек".
Обычно активный центр содержит две области.
Первая – это область (карман, складка) специфичности, которая
распознает необходимый субстрат и прочно связывается с ним.
Вторая область является каталитической, в которой собственно и
происходят химические трансформации субстрата в продукт.
Область специфичности (которой зачастую является практически
весь активный центр) в большинстве ферментов является необходимым
компонентом, поскольку каталитический центр обычно стимулирует протекание достаточно экзотических химических преобразований и, при
этом, сама структура каталитического центра должна быть "подогнана"
под субстрат для оптимизации каталитического процесса, а не просто для
связывания субстрата.
Типичные "допуски" при "подгонке" ферментов и их субстратов составляют доли нанометров. Именно такая высокая точность обеспечивает
экстраординарную специфичность ферментов. Природные ферменты в
большинстве своем способны отличать молекулы субстратов, различаю132
щихся одним единственным атомом. Они также демонстрируют высокую
стереоспецифичность, четко разделяя левые и правые формы молекул
или синтезируя только одну из множества возможных форм продукта.
Стабилизация ферментами переходного состояния химических
реакций. После присоединения субстрата к ферменту фермент формирует белковое окружение, которое стимулирует необходимые химические
преобразования. Ферменты именно потому и способны катализировать
химические реакции, что они стабилизируют промежуточное, переходное
состояние реакции. Это достигается различными способами, выбор которых определяется спецификой конкретной реакции.
(1) Иногда химические группы соседних аминокислот или простетических групп воздействуют на субстрат, модифицируя его электронную
структуру и делая его (или некоторый его участок) более реакционноспособным.
Заряженные аминокислоты могут поляризовать близлежащие химические связи субстрата, облегчая преобразование связей определенного
атома или, наоборот, активируя определенный атом для его "атаки" на
конкретную химическую группу.
Водородная связь может стабилизировать ту конформацию субстрата, которая обычно редко встречается в молекуле свободного субстрата, но которая как раз и нужна для осуществления данной реакции.
(2) Во многих случаях формирование переходного состояния может
приводить к образованию нестабильных заряженных форм молекулы с
одним или несколькими атомами, находящимися в неоптимальном состоянии. Такое состояние может быть стабилизировано посредством размещения рядом с таким атомом противоположно заряженной
аминокислоты. В этом случае стабилизировать переходное состояние будет электростатическое взаимодействие.
(3) Ферменты могут также индуцировать геометрические напряжения в субстратах. В случае, когда геометрия субстрата изменяется в ходе
реакции, форма активного центра является комплементарной именно переходному состоянию субстрата, а не его исходной форме. В этом случае
связывание субстрата с таким активным центром фермента будет индуци-
133
ровать трансформацию субстрата из исходного состояния в переходное
состояние.
Использование ферментами химических инструментов для проведения реакций. Большинство ферментов используют специфические
химические инструменты для непосредственного химического воздействия не субстрат. Важно, что эти инструменты возвращаются в исходное
состояние после того, как фермент завершит химические преобразования
субстрата.
В этом и состоит определение катализатора: он может претерпевать некоторые изменения в ходе реакции, чем он собственно и способствует её интенсификации, но он обязательно возвращается в исходное
состояние, после чего он снова готов катализировать эту же реакцию.
(1) Ферменты обычно используют реакционноспособные аминокислоты для направленной химической модификации субстратов.
Например, многие ферменты используют определенные аминокислоты для переноса атома водорода в пределах молекулы.
В частности, для этого часто используется гистидин. При нормальных физиологических условиях достаточно легко удалить один из водородных атомов гистидина, а затем вернуть его на место.
Гистидин используется во многих реакциях, в которых перестраивается структура молекулы. На гистидин переносится атом водорода, а затем этот атом возвращается на молекулу субстрата, но уже в другую
позицию. В результате либо изменяется геометрия молекулы, либо смещается местоположение двойной связи в молекуле субстрата.
(2) В других реакциях требуется более "силовое" воздействие. В таких случаях аминокислоты ферментов, атакуя субстрат, формируют ковалентную связь с субстратом.
Как правило, получившееся переходное состояние является нестабильным и на следующем этапе реакции либо эта вновь сформированная
связь, либо одна из других нестабильных связей разрушается и образуется
необходимый продукт реакции.
Так, например в сериновой протеазе серин атакует пептидную связь
в субстрате, разрывая пептидную цепь, и образует нестабильную связь с
134
одним из фрагментов. После чего в активный центр входит молекула воды, диссоциирует на ОН– и Н+, ОН– взаимодействует с субстратом, нестабильная связь рвется и фермент возвращается в исходное состояние.
(3) В некоторых реакциях ферменты добавляют новые атомы и
функциональные группы к растущей молекуле.
Когда мы собираемся сделать новый табурет у себя дома, мы редко
используем действительно исходное сырье. В самом деле, мы не рубим
деревья (на древесину) и не добываем железную руду (чтобы сделать
гвозди). Мы просто идем в магазин строительных товаров и покупаем
нужные доски, брус и гвозди.
Аналогично и ферменты обычно строят новые молекулы из уже
предварительно синтезированных определенных химических групп, которые легко добавить к создаваемой молекуле. Многие молекулы являются
носителями таких специфических атомов и групп. На рисунке 81 приведены примеры таких молекул.
Рисунок 81 – Некоторые малые молекулы – переносчики химических групп. На
рисунке показаны: 1 – аденин; 2 – участки молекул, которые легко отдают химические
группы 3–5; 3 – фосфат-ион; 4 – гидрид-ион Н–; 5 – метильная группа
Серым цветом на рисунке 81 показаны "носители" на основе аденина, которые служат для распознавания этих молекул и фиксированного
135
связывания их с ферментами. Светло-серым цветом показаны те участки
молекул (2), которые легко отдают химические группы (3,4,5), а сами эти
группы (3,4,5) показаны темно-серым цветом.
АТФ (ATP) легко отдает фосфат (3), поскольку существует электростатическое отталкивание между отрицательно заряженными фосфатными группами. Никотинамидадениндинуклеотид, НАД (NAD), в форме
НАДН (рисунок 82) переносит гидрид-ион (Н–, атом водорода с дополнительным электроном).
Аденозилметионин (adoMet) переносит метильную группу СН3, которая присоединена к атому серы (рисунок 84). Когда метильная группа
удаляется с adoMet, атом серы переходит в более выгодное состояние, в
котором он связан с двумя, а не с тремя, соседними атомами.
Рисунок 84 – Схема молекулы adoMet
Рисунок 82 – Схема молекулы НАДН
Уход гидрид-иона с НАД (реакция НАДН→НАД⊕) переводит последний в более стабильную ароматическую структуру (рисунок 83).
Рисунок 83 – Схема молекулы НАД⊕
136
Различные молекулы-носители (коферменты) переносят различные
группы, присоединенные к носителям нестабильными связями. Коферменты, в свою очередь, должны быть предварительно синтезированы для
дальнейшего их использования ферментами.
(4) Для переноса всего лишь нескольких электронов в некоторых реакциях в ферментах, как правило, используются ионы металлов, поскольку они могут легко переключаться между разными зарядовыми
состояниями.
Ионы меди и цинка прочно удерживаются внутри небольших аминокислотных кластеров.
С другой стороны, ион железа, обычно захватывается в центре гема
– достаточно большой молекулярной структуры, которая, в свою очередь,
расположена внутри глубокого кармана в теле фермента.
Необычные атомы металла, такие как молибден и ванадий, используются тогда, когда необходимо приложить большую силу, как, например,
137
в случае разрыва молекулярных связей в молекуле азота, который катализирует фермент нитрогеназа (ЕС 1.18.6.1).
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что называется активным центром фермента?
2. Назовите четыре процесса, происходящие в фермент-субстратном
комплексе, которые отличают ферментативные реакции от неферментативных реакций.
3. Что такое "стандартный дефект" макромолекулы белка?
4. Какие четыре механизма играют главную роль при связывании
субстрата в активном центре фермента и образовании комплекса
фермент-субстрат в воде?
5. Какие две модели, учитывающие образование фермент-субстратного комплекса, были исторически первыми?
6. Опишите структуру фермента протеин-киназа А.
7. Какая структурная особенность регуляторных доменов позволяет
обратимо присоединять к ним каталитические субъединицы протеин-киназы А?
8. Опишите протекание реакции изомеризации с участием фермента
триозофосфатизомераза.
9. За счёт каких факторов снижается энтропия в ферментативных
реакциях?
10. Какие две функционально различные области поверхности
белковой молекулы обычно содержат в себе активные центры
ферментов?
11. Какими способами достигается стабилизация переходного состояния в ферментативных реакциях?
12. Какие существуют химические инструменты для химического
воздействия фермента на субстрат?
13. Какие функциональные группы переносят молекулы АТФ, НАД и
adoMet?
14. В каких случаях возникает необходимость использования ионов
металлов, которые встроены в молекулы ферментов?
138
Глава 7
МЕХАНИЗМЫ ФЕРМЕНТАТИВНОГО КАТАЛИЗА
7.1. МЕХАНИЗМЫ РЕГУЛЯЦИИ ФЕРМЕНТАТИВНОЙ АКТИВНОСТИ
Рассмотрим общие принципы регуляции функций белков вообще и
регуляции ферментативной активности в частности. Основные механизмы
управления каталитической активностью фермента связаны со следующими явлениями и процессами:
1) аллостерия;
2) кооперативность;
3) связывание с лигандами (ингибиторами, активаторами, эффекторами, индукторами);
4) существование белковых переключателей.
Аллостерия. Главным механизмом регулирования функции белков
является аллостерическое регулирование – изменение третичной или четвертичной структуры белка в ответ на связывание с любым лигандом
(ингибитором, активатором, субстратом или всеми тремя).
Принцип аллостерии был сформулирован Монодом с соавторами в
1965 году, причем они считали, что обнаружили второй после открытия
структуры ДНК секрет жизни.
Они определили аллостерические белки как белки, которые могут
находиться в двух (или более) стабильных структурных конформациях и
могут легко переключаться между этими состояниями.
Аллостерическим механизмом регуляции активности ферментов
называют регуляторный механизм, в котором контроль активности фермента реализуется путем изменения конформации белковой молекулы (изменением топологии третичной структуры глобулы), индуцируемого
связыванием метаболита-регулятора в особом (аллостерическом) центре, пространственно удаленном от активного центра (рисунок 85).
139
Изменение конформации молекулы фермента влечет за собой изменение каталитических характеристик активного центра.
Метаболит-регулятор, модифицирующий активность фермента подобным образом, называют аллостерическим эффектором.
Рисунок 85 – Схема функционирования аллостерического фермента: а – состояния аллостерического фермента зависят от его пространственной организации;
б – аллостерическая активация достигается связыванием активатора (положительного
эффектора); в – аллостерическая инактивация происходит благодаря связыванию ингибитора (отрицательного эффектора)
центрами, но и между центрами одного сорта (между активными или между аллостерическими центрами).
Аллостерические ферменты являются олигомерами, состоящими из
двух или более мономеров (рисунок 85). Аллостерические ферменты могут существовать в одном из двух обратимо связанных состояний – активном и неактивном.
Каждый лиганд (субстрат, эффектор), способный образовывать
комплекс с белком, может связываться с каждой белковой субъединицей
– субстрат в активном центре, эффектор в регуляторном.
Связывание эффектора с одной субъединицей (рисунок 85(б,в)) вызывает постепенное изменение конформации других субъединиц, приводящее в конечном счете к переходу аллостерического фермента в
активное состояние.
Обратный переход фермента из активного состояния в неактивное
сопровождается изменением субстрат–связывающей активности. В процессе превращения одной конформации в другую четвертичная структура
белка (число субъединиц, доменный состав фермента), как правило, остается неизменной.
Протеин-киназа А является исключением из этого правила. Связывание протеин-киназы А с лигандом (цАМФ) индуцирует аллостерическое освобождение каталитической субъединицы.
Многие мультидоменные ферменты претерпевают аллостерические
превращения, которые изменяют структуру и свойства субъединиц, но
не вызывают отделение субъединиц друг от друга.
При этом активность белка в состоянии с присоединенным лигандом
отличается от активности состояния без лиганда.
Например, шаперонин hsp60 (рисунок 58), состоящий из двух мультисубъединичных колец, может существовать в двух состояниях:
1) "напряженное" пептид-связывающее состояние,
2) "релаксированное" пептид-высвобождающее состояние.
Олигомерная молекула фермента, состоящая из нескольких субъединиц, может содержать несколько активных центров и несколько аллостерических центров для определенного эффектора. В таком олигомере
возможны взаимодействия не только между активным и аллостерическим
Связывание АТФ с одним из колец шаперонина вызывает расширение полости обеих колец и переключение в релаксированное состояние.
140
141
Аллостерические ферменты принимают участие в контроле метаболизма в виде мулътиферментных систем. Влияние на метаболизм достигается за счет обратной, положительной или отрицательной связи.
Связывание Са2+ с кальмодулином индуцирует изменение его конформации, в результате чего кальмодулин обвивается вокруг α-спиралей
различных белков, тем самым резко изменяя их активность.
Кооперативность. Кооперативностью называется явление, при котором связывание с белком одного лиганда изменяет величину сродства
белка по отношению к связыванию последующих лигандов.
Кооперативность позволяет мультидоменным белкам гораздо сильнее реагировать на изменения в концентрации лиганда, чем это следовало
бы из простого химического равновесия при данной концентрации.
В случае положительной кооперативности последующее связывание облегчается.
В случае отрицательной кооперативности последующее связывание ингибируется.
Например, связывание кислорода одним из четырех доменов гемоглобина индуцирует такие конформационные изменения, которые облегчают связывание кислорода с тремя оставшимися доменами –
положительная кооперативность.
Кальциевые переключатели. Работу кальциевых переключателей
рассмотрим на примере белков кальмодулинов.
Ионные насосы в клеточной мембране поддерживают низкую концентрацию ионов Ca2+ в цитозоле (<10–7 М), выкачивая ионы из клетки
или закачивая их в эндоплазматический ретикулум. Соотношение концентраций кальция в цитозоле и вне его достигает 10–100 раз.
Сенсорами увеличения концентрации кальция в цитозоле являются
2+
Са -связывающие белки, в частности принадлежащие к EF-handсемейству, все члены которого имеют мотив "спираль-петля-спираль", обсуждавшийся ранее (рисунок 39).
Основатель (прародитель) этого семейства белок кальмодулин присутствует во всех эукариотических клетках, как в виде субъединицы
сложных белков, так и индивидуально в виде мономера. Гантелеобразная
молекула кальмодулина содержит четыре Са2+-связывающих центра,
имеющих константу равновесия К ≈ 10–6 М (рисунок 86).
142
Рисунок 86 – Превращение, стимулируемое связыванием Са2+ с кальмодулином
Таким образом, кальмодулин и родственные ему EF-hand-белки
выполняют функцию переключающих белков (белков-переключателей),
изменяющих активность других белков согласованно с изменением концентрации кальция в цитозоле.
ГТФазы. Другую группу внутриклеточных белков-переключателей
составляет суперсемейство ГТФаз (рисунок 87).
К ГТФазам, в частности, принадлежат такие распространенные бел-
ки, как белок Ras и Gα-субъединица тримерного G-белка. И Ras, и Gα связываются с плазматической мембраной и играют ключевую роль в таких
ключевых клеточных процессах, как (1) клеточная сигнализация, (2) клеточное деление и (3) дифференциация. Другие члены этого суперсемейст143
ва ГТФаз принимают участие в (4) процессе синтеза белка, (5) в транспорте белков между ядром и цитоплазмой, (6) в формировании окаймленных пузырьков и их слиянии с определенной мембраной, (7) в
процессах реорганизации актинового цитоскелета.
Все ГТФазные переключающие белки существуют в двух формах:
(1) активная ("вкл") форма с присоединенной молекулой ГТФ
(гуанозинтрифосфат, GTP), которая управляет активностью
специфических белков,
(2) неактивная ("выкл") форма со связанной молекулой ГДФ
(гуанозиндифосфат, GDP).
Такими белками, например, являются белки GAP (GTPaseaccelerating proteins) и RGS (regulators of G-protein signaling), ускоряющие гидролиз ГТФ. Белки GDI (guanine nucleotide dissociation inhibitor),
напротив, замедляют гидролиз. Реактивация ГТФазного белкапереключателя ускоряется белками GEF (guanine nucleotide-exchange factors).
Циклическое фосфорилирование-дефосфорилирование. Одним
из наиболее распространенных механизмов регуляции активности белков
является фосфорилирование – присоединение или отсоединение фосфатной группы к оксиаминокислотам: тирозину, серину и треонину (рисунки 27, 30, 31).
Фосфорилирование катализируют протеин-киназы (трансферазы), а
дефосфорилирование – протеин-фосфотазы (гидролазы) (рисунок 88).
Рисунок 87 – Циклирование ГТФазы между активной и неактивной формами
ГТФазная активность этих белков-переключателей приводит к
медленному гидролизу ГТФ в ГДФ, "выключая" белок. Последующая замена ГДФ на ГТФ, восстанавливающая активную форму, происходит ещё
более медленно.
Такая активация белка носит временный характер и управляется
другими белками, осуществляющими аллостерическое регулирование
ГТФазного белка-переключателя.
Хотя обе реакции являются необратимыми, согласованная "работа"
киназ и фосфотаз образует своеобразный киназно-фосфотазный "переключатель", управляющий функциями многих клеточных белков.
144
145
Рисунок 88 – Регуляция активности белка киназно-фосфотазным переключателем
Фосфорилирование изменяет заряд белка, что, вообще говоря, приводит к изменению конформации белковой молекулы. Этот эффект может
значительно изменить силу связи лиганда с белком, что приводит к резкому усилению или ослаблению активности белка.
Тот факт, что киназы и фосфотазы составляют около 3% всех белков клетки дрожжей, подтверждает важность реакций фосфорилирования
и дефосфорилирования даже в простейших клетках.
Все классы белков, включая структурные белки, ферменты, мембранные каналы, сигнальные белки – регулируются киназно-фосфотазными переключателями.
Различные протеин-киназы и фосфотазы субстратно-специфичны к
различным белкам, что обеспечивает возможность регулировки различных метаболических реакций. Причем некоторые из этих ферментов действуют только на специфический белок, а некоторые специфичны к
достаточно широкому набору белков. В последнем случае реализуется
интегральная реакция различных белков в ответ на "срабатывание" одного "переключателя".
Часто субстратом киназ и фосфотаз бывают другие киназы и фосфотазы, что позволяет клетке создавать ферментативные каскады –
сложные взаимозависимые системы (сети) тонкой регулировки метаболических процессов.
Энтерокиназа (аминопептидаза, секретируемая клетками поверхности тонкого кишечника) превращает трипсиноген в трипсин, который в
свою очередь "обрезает" химотрипсиноген до химотрипсина. То, что эти
протеазы активируются таким сложным образом, защищает ткани печени
от "самопереваривания" ферментами, которые они же сами и синтезируют.
Например, фермент трипсин (рисунок 89) активизируется вырезанием регуляторного пептида, который блокирует каталитический центр,
находящийся внутри глубокой впадины на поверхности фермента.
Механизм регуляции белковой активности путем протеолитического разрезания полипептидной цепи. Протеолиз необратимо активирует или деактивирует некоторые белки. Механизм регуляции белковой
активности путем протеолитического разрезания полипептидной цепи
белка принципиально отличается от механизмов "включить-выключить".
Этот механизм наиболее часто используется для управления активностью
гормонов (например, инсулина) и пищеварительных протеаз.
Примером таких протеаз являются трипсин (ЕС 3.4.21.4) и химотрипсин (ЕС 3.4.21.1), которые синтезируются в клетках печени и секретируются в тонкий кишечник в виде неактивных зимогенов – трипсиногена
и химотрипсиногена, соответственно.
Это, в частности, важно в случае синтеза пищеварительных ферментов, которые, после синтеза в клетке, должны оставаться безопасными
(неактивными) до тех пор, пока они не секретируются из клетки.
Протеолитическое разрезание также используется для регуляции
свертывания крови, когда компоненты, формирующие сгусток (тромб)
присутствуют в крови в большой концентрации, но активируются только
в месте повреждения кровеносного сосуда. Это позволяет ассемблировать
тромб размером порядка миллиметра за время порядка секунды.
Разрезание также используется иммунной системой, когда молекулы
активизируются только в необходимом месте организма. Во всех этих
случаях белок синтезируется в форме профермента, с лишними сегмен-
146
147
Рисунок 89 – Активизация трипсина протеолитическим вырезанием регуляторного пептида
тами, которые блокируют активный центр или удерживают фермент в неактивной форме.
Протеолитические разрезание напоминает выдергивание чеки из
гранаты – активизация фермента происходит вследствие удаления блокирующего белкового сегмента.
Другим примером использования протеолитического разрезания
для формирования функциональной структуры белка является использование протеолитических систем в ходе биосинтеза малых белков, когда
сначала белок синтезируется в виде про-формы, значительно превышающей по размерам сам белок.
Примером использования такой методики является синтез и фолдинг инсулина.
Инсулин – это очень маленький белок, собранный из двух отдельных цепей А и В, соединенных дисульфидными мостиками (рисунок 90).
Рисунок 90 – Схема пептидных цепей инсулина
Средний фрагмент, образующийся из участков (3) и (4) необходим
для правильного самоассемблирования инсулина. Этот участок вырезается после завершения фолдинга. Финальный TAG кодон участка (5) является стоп-кодоном.
Рисунок 91 – Фрагмент генома человека с участками, кодирующими инсулин
Фрагмент генома человека, в котором закодирован инсулин показан
на рисунке 91. Он содержит два участка (2) и (5), кодирующих две полипептидные цепи А и В, входящие в молекулу инсулина, разделенные некодирующим сегментом.
Первоначально каждая из цепей синтезируется более длинной: первая полипептидная цепь содержит участки (1), (2) и (3), вторая – участки
(4) и (5).
Участок (1) является временной адресной последовательностью, которая направляет инсулин в секреторную систему клетки, выводит его за
пределы клетки, и затем удаляется.
Функциональная молекула инсулина, содержащая две полипептидные цепи, показана на рисунке 92.
Белковая нить, соответствующая участку (2) показана белым цветом, а участку (5) – серым. Черным показаны атомы серы, образующие
дисульфидный мостик между цепями А и В.
Стабильность инсулина в значительной степени обеспечивается
внутренними дисульфидными мостиками. Очень сложно (а может быть
и невозможно) спроектировать искусственный белок, имеющий размер
инсулина, который бы самопроизвольно сворачивался бы в единственную
функциональную конформацию.
148
149
Природа разрешила эту проблему просто – инсулин синтезируется в
составе полипептида значительно большей длины, фолдинг которого и
формирует пространственную структуру инсулина. Затем, после окончания фолдинга и образования дисульфидных мостиков, "лишние" участки
белка удаляются, а то, что остается после такой "стрижки", и является
функциональным инсулином.
Рисунок 92 – Схема молекулы инсулина: 1 – полипептид А, 2 – дисульфидный
мостик
7.2. МЕХАНИЗМЫ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
Электронно-конформационные взаимодействия в ферментативном катализе. Конформационные изменения в белковой глобуле
носят релаксационный характер и характеризуются целым набором различных времен. Они происходят, как правило, намного медленнее, чем
чисто электронные переходы.
Быстрые изменения электронного состояния молекулы белка (например, восстановление атома Fe3+ активного центра цитохрома) нарушают исходное равновесное конформационное состояние и приводят к
каскаду последовательных конформационно-релаксационных актов, носящих направленный характер. Именно это обстоятельство составляет физическую
основу
конформационно-релаксационной
концепции
ферментативного катализа Блюменфельда. Появление продукта реакции
150
рассматривается здесь как закономерный результат электронно-конформационных взаимодействий в комплексе фермент-субстрат.
Предполагают, что конформационные изменения ферментсубстратного комплекса, следующие за изменением электронного состояния субстрата в активном центре фермента, носят характер направленной
релаксации и включают процессы превращения молекул субстрата в молекулы продукта.
Элементарный акт ферментативной реакции заключается в конформационном изменении фермент-субстратного комплекса, а скорость
превращения субстрат-продукт определяется скоростью этого конформационного изменения.
Последовательность событий представляется следующим образом.
Изменение электронного состояния и локальные изменения геометрии активного центра и субстрата после сорбции субстрата S на ферменте E
происходят быстро за времена колебательной релаксации (10–12–10–13 с).
Они затрагивают только часть молекулы – выделенные химические связи
субстрата и функциональных групп активного центра, но не остальную
большую часть белковой глобулы.
Следовательно, в целом на этом этапе макромолекулярный комплекс находится в конформационно-неравновесном состоянии.
Затем происходит медленная релаксация фермент-субстратного
комплекса к новому равновесию и превращение субстрата в продукт:
~
S + E → SE * → EP ,
~
где E * – неравновесное, а E – новое равновесное конформационное состояние белковой глобулы фермента. Химическое изменение субстрата,
включающее перегруппировку атомов вслед за разрывом химических связей, реализуется здесь как часть конформационного изменения макромолекулярного комплекса.
На следующей стадии происходит распад комплекса фермент–
продукт:
~
~
EP → E + P .
151
Эта стадия также сопровождается быстрыми локальными изменениями в активном центре и сольватационными изменениями продуктов
реакции, переходящих в объем. Фермент остается в конформационном
~
состоянии E , которое после отрыва продукта становится неравновесным
и напряженным.
Наконец, на заключительном этапе происходит медленная конформационная релаксация свободной молекулы фермента к исходному равно~
весному состоянию: E → E .
Таким образом, конформационное изменение происходит в условиях существенной конформационной неравновесности. Координата реакции совпадает с координатой конформационной релаксации, которая
протекает по определенным степеням и носит направленный характер:
Именно наличие выделенных механических степеней свободы позволяет рассматривать смещения, происходящие в разных областях макромолекулы, как изменения, совершающиеся в один акт. Энергия,
сосредоточенная на этих медленно релаксирующих степенях свободы, не
диссипирует быстро в теплоту за счет размена по другим обычным степеням свободы, а используется фактически для обеспечения направленного
характера релаксационных процессов в ферментативном катализе.
С такой нетрадиционной точки зрения, теряет непосредственный
смысл использование понятий энергии и энтропии активации, как это делают в теории активированного комплекса. Зависимость скорости ферментативной реакции от температуры определяется не числом активных
молекул с энергией, достаточной для преодоления барьера, а влиянием
температуры на конформацию макромолекулы и, следовательно, на путь
и скорость её последующей релаксации.
Все молекулы субстрата, образовавшие "правильный" комплекс с
ферментом, претерпевают химическое превращение в результате самопроизвольной релаксации фермента к новому конформационному состоянию.
Конечно, с термодинамической точки зрения, общей движущей силой процесса является разность химических потенциалов субстрата и продукта. Однако она определяет лишь число встреч молекул фермента и
субстрата, но не сам активационный механизм превращения ферментсубстратного комплекса.
Таковы в основном современные представления об общих механизмах ферментативного катализа.
Понимание механизмов конкретных каталитических требует детального изучения электронных взаимодействий в активном центре между функциональными группами.
Эти взаимодействия осуществляются в целом на гораздо более коротких расстояниях по сравнению с нековалентными атом-атомными
взаимодействиями, определяющими характер внутримолекулярной динамики белковой глобулы фермента.
Кроме того, нековалентные фермент-субстратные взаимодействия
реализуются в системах, состоящих из многих сотен атомов, в то время
как электронные, чисто химические взаимодействия происходят в активном центре между ограниченным числом атомов, принадлежащих функциональным группам.
Нековалентные взаимодействия приводят к конформационным изменениям, характерные времена которых намного больше, чем времена
колебательной релаксации, сопровождающие чисто электронные переходы.
На первом этапе катализа определяющее значение приобретает характер структурно-динамического взаимодействия фермент-субстрат.
На втором этапе, после образования активного комплекса, основную роль уже играют квантовомеханические электронные процессы взаимодействия между ограниченным числом атомных групп в активном центре.
Следовательно, конформационно-динамические аспекты ферментативного катализа, связанные с формированием химически активной конфигурации, можно рассматривать независимо от квантовомеханической
природы элементарного акта разрыва связей субстрата в активном центре.
152
153
~
E → E* → E → E .
Это обстоятельство отражает природу ферментативного акта как следствие электронно-конформационных взаимодействий в молекуле белкафермента.
Термодинамика ферментативной реакции. Ферменты ускоряют
реакции, увеличивая их константы скорости. Обычно рассмотрение этого
эффекта проводят в рамках теории переходного состояния или активированного комплекса (рисунок 93).
Константа скорости равна
k =χ
⎛ ΔG ≠ ⎞
k BT
exp ⎜ −
⎟,
h
⎝ RT ⎠
где ΔG ≠ – разность значений свободных энергий для переходного и осk T
новного состояний; χ – трансмиссионный коэффициент (~1); B = ω опh
ределяет частоту тепловых флуктуаций. При k BT ≈ 0,025 эВ ω =1013 с–1, а
соответственно время сохранения переходного состояния составляет
~10–13 с.
Используя уравнение Гиббса-Гельмгольца, ΔG0≠ = ΔH 0≠ − T ΔS0≠ , получаем выражение
k =χ
Рисунок 93 – Изменение энергии реагентов вдоль координаты реакции
Считают, что реагенты, находящиеся исходно в основном состоянии, образуют комплекс, который активируется с образованием переходного состояния. Этому состоянию соответствует максимум на кривой
изменения энергии реагентов вдоль координаты реакции. Продукты реакции возникают при движении вдоль координаты реакции из переходного
состояния.
В теории активированного комплекса предполагается, что существует термодинамическое равновесие между переходным и основным состояниями, которому соответствует константа равновесия, равная
отношению концентраций активных комплексов и исходных реагентов.
Тогда по разности свободных энергий этих состояний можно найти концентрацию переходных комплексов, а затем скорость реакции путем умножения этой концентрации на константу скорости его распада k .
154
⎛ ΔH ≠ ⎞
⎛ ΔS ≠ ⎞
k BT
exp ⎜ −
⎟ exp ⎜
⎟.
h
⎝ RT ⎠
⎝ R ⎠
При образовании активного комплекса происходит снижение энтропии ( ΔS ≠ < 0 ) вследствие формирования вполне определенной взаимной ориентации молекулярных групп реагентов по сравнению с их
хаотическим расположением в исходном состоянии. Таким образом, энтропийный ( ΔS ≠ < 0 ) и энергетический ( ΔH ≠ > 0 ) факторы действуют в
направлении снижения скорости реакции.
Ускорение ферментативных реакций по сравнению с соответствующими неферментативными означает на языке формальной кинетики,
что величина активационного барьера ΔG ≠ в ферментативных реакциях
снижается. Это может происходить за счет снижения абсолютной величины S ≠ , а также за счет уменьшения энтальпии активации ΔH ≠ .
Понижение энтропийной части происходит в результате фиксации
субстрата на ферменте в конфигурации активных групп, обладающей и
более низкой энтропией по сравнению со свободным сочетанием реагентов. Следовательно, в таком комплексе, исходно близком к переходному
155
состоянию, уменьшение энтропии при образовании самого переходного
состояния не должно быть уже столь большим по абсолютной величине,
как в случае свободных реагентов. Роль энтропийного фактора
Эта система может быть переведена из начального в конечное состояние двумя путями:
⎛ ΔS ≠ ⎞
exp ⎜
⎟ 1,
⎝ R ⎠
1)
снижающего скорость реакции, уменьшается в ферментативном процессе
по сравнению с обычной реакцией.
Избыток энергии, выделяющейся при связывании субстрата, должен хотя бы частично переходить в теплоту, чтобы скомпенсировать
уменьшение энтропии при образовании комплекса. С энергетической точки зрения, происходящая стабилизация и уменьшение собственной энергии комплекса должны были бы замедлять катализ, где требуется
преодоление активационного барьера.
Однако в схемах энергетического катализа предполагают, что осуществляется не только (1) фиксация конфигурации субстрата, но и (2)
создание напряжения фермент-субстратного комплекса, способствующего реакции. При этом происходит и снижение энергии активации химической реакции за счет концентрации энергии напряжения на атакуемой
связи.
Энергия, необходимая для создания такого напряженного состояния
связи, черпается из энергии сорбции, которая, как предполагают, не расходуется полностью в теплоту, а может быть запасена в белковой части
фермента и сконцентрирована в области образовавшихся ферментсубстратных контактов.
Рассмотрим взаимодействие двух частиц: фермент X − E и субстрат
Y − R , каждая из которых имеет два реагирующих центра.
В первых центрах ( X и Y ) происходят химические превращения с
относительно высокой свободной энергией активации.
Вторые центры ( R и E ) обеспечивают ориентировку и фиксацию
двух частиц, на них происходят – сорбционные взаимодействия, которые
идут весьма быстро (с малой свободной энергией активации).
2)
156
X
E
X
E
+
+
Y
R
Y
R
→
→
X Y
E •R
X
E
→
X
E
+ Продукты ,
+ Продукты .
Первая реакция моделирует ферментативный, а вторая – обычный
гомогенно-каталитический процесс, в котором нековалентные (сорбционные) взаимодействия между группами R и E не реализуются.
Механизм сближения и ориентации. Пусть образование переходного состояния реакции (2) условно происходит через две стадии: на первой из них молекулы реагентов необходимо сблизить в положение с тесно
примыкающими реагирующими центрами X и Y . Лишь затем может идти собственно химическое взаимодействие. Поэтому условно свободную
энергию активации можно разделить на два члена:
≠
≠
ΔG ≠ = ΔGсближ
+ ΔGвнутр
.
≠
соответствует главным образом термодинамичеВеличина ΔGсближ
ски невыгодному понижению энтропии, обусловленному остановкой поступательного (для одной частицы), а также вращательного и других
движений, что необходимо для сближения и взаимной ориентации реагирующих частиц.
Последующее химическое взаимодействие (идущее "внутримолекулярно" в таком условно замороженном комплексе между реагентами) ха≠
.
рактеризуется свободной энергией активации ΔGвнутр
В реакции, протекающей по ферментативному пути (1) (исходное
состояние – фермент-субстратный комплекс), затраты свободной энергии
157
≠
типа ΔGсближ
в большей части должны отсутствовать. Дело в том, что в
комплексе XE•RY за счет свободной энергии сорбции Е•R погашено поступательное движение одной из частиц, а возможно (в зависимости от
конкретной модели) сориентированы по отношению друг к другу (хотя
бы частично) реакционные центры Х и Y.
Иными словами, при образовании фермент-субстратного комплекса
происходит перемещение вдоль координаты реакции одновременно также
и системы Х + Y. В результате исходное состояние ферментативной реакции (которое иногда называют комплекс Михаэлиса) уже содержит
некоторые элементы процесса активации, которые необходимы для
Для объяснения высокой эффективности ферментативного катализа
Эмиль Фишер предложил образное сравнение: "активный центр организован так, что субстрат входит в него как ключ в замок".
В свете современных представлений этого явно недостаточно. Если
говорить на языке Эмиля Фишера, то, во-первых, ключ должен был бы
быть плохо подогнанным к замку и, кроме того, нужно было бы принять
во внимание также и силу, которая ключ повернула бы.
Механизм, с помощью которого ферменты реализуют принцип
сближения и ориентации, иллюстрирует модель, представленная на рисунке 94.
достижения переходного состояния (XY) ≠ .
Для этого необходимо, чтобы строение активного центра в высшей
мере было комплементарно по отношению к той структуре молекуле субстрата, которую она должна принять в переходном состоянии реакции.
Именно поэтому активный центр фермента расположен обычно в
складках полипептидной цепи, образующих как бы "щель". Где-то в глубинных участках этой щели расположены аминокислотные остатки, взаимодействующие с субстратом.
Благодаря такой структуре активного центра при переходе молекулы субстрата из свободно движущегося состояния (из раствора) в сорбированное состояние (когда она "втискивается" в активный центр)
происходит необходимое для реакции "замораживание" вращательных
степеней свободы и сближение её с каталитически активными группами
белка.
Однако структурных предпосылок (налагающих требования к геометрии активного центра) недостаточно для катализа. Термодинамически
невыгодному процессу сближения и ориентации прежде всего нужна
движущая сила, благодаря которой суммарный процесс пошел бы спонтанно.
В ферментативном катализе роль такой движущей силы играет
свободная энергия сорбции субстрата на ферменте.
158
а
б
Рисунок 94 – Снижение свободной энергии активации химического превращения фермент-субстратного комплекса за счет эффекта сближения и ориентации
Пусть системе, изображенной на рисунке 94(а) присущи какие-то
определенные значения величин свободной энергии, характеризующих
сорбцию группы R на ферменте и последующее химическое взаимодействие Х и Y.
Для другого субстрата (рисунок 94(б)), содержащего в молекуле два
фрагмента R и R', способных сорбироваться на ферменте, потенциальная
свободная энергия сорбции в принципе должна быть термодинамически
более благоприятной. С другой стороны, образование ферментсубстратного комплекса в этом случае явно сопряжено с большими ограничениями как внешних, так и внутренних вращательных степеней свободы, чем в системе (а).
159
Поэтому рост свободной энергии сорбции, вообще говоря, компенсируется сопровождающими сорбцию потерями энтропии. Однако, системы (а) и (б) на рисунке 94 отличаются по свободной энергии активации
последующего химического взаимодействия Х + Y, протекающего в фермент-субстратном комплексе.
В модели, изображенной на рисунке 94(а), образованию переходного состояния (XY) ≠ должно предшествовать дальнейшее сближение и
ориентация реагирующих центров Х и Y, что потребует существенных
затрат энтропии и внесет, соответственно, термодинамически невыгодный
вклад в свободную энергию активации.
В структурно усложненной модели (рисунок 94(б)), обладающей
более высокой потенциальной энергией сорбции, реагирующие центры
уже сближены, а возможно (в зависимости от более конкретных условий
модели) и частично сориентированы. Следовательно, свободная энергия
активации, характеризующая превращение фермент-субстратного комплекса, будет в этом случае более благоприятной.
Механизм индуцированного соответствия. Согласно теории индуцированного соответствия, выдвинутой Кошландом, в свободном ферменте (в отсутствие субстрата) каталитически активные группы Х и Х'
расположены так, что они не могут одновременно взаимодействовать с
субстратным фрагментом Y (рисунок 95(а)).
Поскольку молекула фермента довольно гибкая, а субстрат имеет
жесткую структуру, энергетически менее предпочтительная, но каталитически активная конформация активного центра образуется лишь в фермент-субстратном комплексе (рисунок 95(б)). На образование её тратится
часть свободной энергии сорбции.
Впоследствии опыт полностью подтвердил эту гипотезу, но только
для тех белков, которым нужно скрыть обрабатываемый субстрат от конкурирующей с ним воды.
Для действия трипсина, например, этого не нужно, и в нем индуцированного соответствия субстрату не наблюдается: трипсин (а также –
химотрипсин, эластаза, субтилизин и др.) не деформируется и опознает
субстрат по простейшему принципу "ключ-замок".
Индуцированное соответствие достигается смещением либо крупных блоков, либо целых белковых доменов, а не полной перестройкой укладки белковой цепи. Эти смещения происходят в основном путем
мелких локальных деформаций.
Механизм "напряжения". Механизм напряжения (так называемая
модель "дыбы") предполагает, что силы сорбции используются для создания напряжений (деформаций) в молекулах реагирующих компонентов,
способствующих протеканию реакции (рисунок 96). Как молекулы субстрата, так и молекулы фермента могут претерпевать конформационные
изменения.
Рисунок 96 – Схема механизма "напряжения"
а
б
Рисунок 95 – Схема изменений в ферменте, индуцированных субстратом – механизм индуцированного соответствия
В модели "дыбы" предполагается, что активный центр устроен так,
что в результате деформации молекула субстрата активируется т. е.
160
161
приобретает некоторые свойства, важные для образования переходного
состояния реакции. В противном случае, когда жесткой является молекула субстрата, а конформационно лабилен фермент, схему катализа можно
представить так же, как для механизма индуцированного соответствия.
Индуцированное субстратом (или, в противном случае, ферментом)
искажение конформации можно представить как сжатие (или растяжение) связей или изменение углов между связями. В общем случае, рассматривая строение молекулы субстрата или фермента, под "напряжением
структуры" можно понимать также и десольватацию функциональных
групп, принимающих участие в химической реакции.
В реальных системах ни субстрат, ни фермент не являются жесткими молекулами. Поэтому при связывании претерпевают конформационные изменения, как правило, молекулы обоих реагентов. Поэтому
провести четкую грань между различными механизмами катализа не
представляется возможным.
Более того, даже обычный механизм ориентации реагирующих
групп (рисунок 94) в ряде случаев можно трактовать как создание некоторых напряжений в структуре молекул реагентов. Отличие между рассмотренными механизмами состоит лишь в используемых терминах (таких,
как "принудительная ориентация", "индуцированное соответствие", механизм "дыбы", "щелевой эффект" и т. п.) и некоторых частных предпосылках о строении активного центра.
Термодинамическая же сущность всех этих теорий одна: потенциальная свободная энергия связывания (сорбции) субстрата на
ферменте тратится на понижение барьера свободной энергии
активации последующей химической реакции.
бранных так, чтобы, связывая переходное состояние субстрата, они катализировали бы его химическое превращение.
Природные антитела (иммуноглобулины) – это белки, синтезируемые клетками иммунной системы для специфического распознавания и
маркировки (посредством присоединения молекулы антитела) антигенов,
таких как инфицирующие агенты (например, бактерии и вирусы) или определенные чуждые вещества (например, белки или полисахариды в
пыльце растений).
В ответ на появление антигенов организм вырабатывает большое
количество антител, каждое из которых может присоединяться к различным определенным выступающим участкам – антигенным детерминантам или эпитопам – антигенов.
Антитела работают как специфические сенсоры для антигенов, образуя комплексы антитело-антиген, которые стимулируют каскад защитных реакций в клетках иммунной системы.
Все антитела имеют Y-образную форму и образованы из двух идентичных "тяжелых" H-цепей (heavy) и двух идентичных "легких"
L-цепей (light) (рисунок 97). Каждая "рука" (arm) молекулы антитела образована одной H-цепью и одной L-цепью, связанных между собой дисульфидными мостиками. На конце каждой руки расположены шесть
полипептидных петель (по три на каждой цепи), образующих антигенсвязывающий карман – область связывания антигена – участок комплементарности, CDR (complementery-determinig region), к эпитопу антигена.
Механизм катализа за счет преимущественного связывания фермента с переходным (деформированным, напряженным) состоянием субстрата наиболее наглядно проявляется в каталитической функции "абзимов"
(antybody enzyme), или искусственных каталитических антител, ото-
Специфичность антител. Структура и последовательность этих
шести петель у разных антител чрезвычайно разнообразна, что обеспечивает высокую специфичность связывания антитела именно с комплементарным антигеном.
Взаимодействие антиген-связывающего кармана CDR антитела с
эпитопом антигена является комплементарным и топологически – форма
поверхности эпитопа точно совпадает с формой поверхности CDR (рисунок 97(в)), и химически – функциональные группы на обеих поверхностях
дополняют друг-друга при образовании парных нековалентных взаимо-
162
163
7.3. АБЗИМЫ
действий, таких, как водородные связи или электростатические взаимодействия.
а
в
б
г
Рисунок 97 – Антитело: а – схема молекулы антитела; б – структура антитела;
в – специфичность антител; г – В-клетки. 1 – антиген; 2 – H-цепь; 3 – L-цепь; 4 – антиген-связывающий карман CDR
Такой совершенный контакт между поверхностями, стабилизированный системой нековалентных связей, обеспечивает превосходную специфичность связывания антигенов антителами.
164
Специфичность антител настолько высока, что они могут различать
отдельные клетки и, в некоторых случаях, белки, которые отличаются
единственной аминокислотой.
Модификация антител. Антитела синтезируются белыми кровяными тельцами, называемыми В-лимфоцитами или В-клетками (рисунок 97(г)). Антитела расположены на поверхности этих клеток и являются
рецепторами, распознающими специфический антиген.
Связывание этих присоединенных антител данной В-клетки с соответствующим антигеном стимулирует В-клетку к началу размножения и
активного синтеза антител, которые выводятся в плазму крови и обладают
той же специфичностью, что и "сигнальные" антитела на поверхности
В-клетки. Антитела связываются с инфицирующими агентами, затем такие агрегаты либо поглощаются фагоцитами для протеолитической деградации ("клеточного переваривания"), либо деградируют в кровотоке с
помощью специфических ферментов.
В процессе размножения В-клеток у антител может происходить
модификация центров связывания. Те дочерние клетки, у антител которых
центры связывания более эффективны, чаще и прочнее связываются с антигенами и, тем самым, имеют преимущество в дальнейшем росте и размножении. Те же дочерние клетки, центры связывания которых
связываются с антигенами слабее, размножаются хуже. Так осуществляется отбор и "подгонка" иммунной системы под ксенобиотики.
Согласно клонально-селекционной теории чрезвычайное разнообразие антител объясняется тем, что в зародышевых клетках представлены не
целые гены легких и тяжелых цепей антител, а части, фрагменты этих генов. Там эти части собраны в "кассеты" – отдельно много сортов для каждого из трех фрагментов вариабельного домена тяжелой цепи, отдельно –
для легкой цепи; отдельно – константные домены каждой цепи; отдельно
– гибкие линкеры, связывающие домены антитела. При образовании соматических иммунных клеток эти фрагменты генов всячески перетасовываются, а кроме того ещё каким-то неизвестным образом мутируют в
своих гипервариабельных участках, после чего соединяются в целые гены
легких и тяжелых цепей антител.
165
Моноклональные антитела. В-клетки животного, инфицированного данным антигеном, синтезируют множество различных антител,
связывающихся с различными участками (антигенными детерминантами
или эпитопами) этого антигена. В большинстве случаев использование
такой однородной смеси разных антител не целесообразно, необходимо
выделить лишь одно характеристическое антитело. Для этого надо выделить ту единственную В-клетку, которая синтезирует это антитело, и, затем, культивировать её. Однако число актов деления В-клеток
ограничено, поэтому не удается синтезировать необходимое количество
антител.
В конце 70-х годов ХХ века эта проблема была решена. В-клетки
были соединены с "бессмертными" раковыми клетками. Такие комбинированные клетки можно культивировать, синтезируя нужное количество
антител. Такие антитела называются моноклональными антителами, поскольку они произведены клонированием идентичных комбинированных
клеток. Сегодня моноклональные антитела могут быть синтезированы для
практически любого мыслимого антигена.
Абзимы. Для целей ферментативного катализа используют абзимы
– антитела, синтезированные в ответ на введение антигенов, имитирующих переходное состояние каталитической реакции. Например, переходное (‡) состояние реакции изомеризации
представляет собой (в отличие от начального и конечного состояний)
плоскую систему из трех колец. Для выработки антител к переходному
состоянию такой формы в качестве антигена использовали подобную, но
стабильную молекулу, которая также имела три кольца в своей структуре.
166
Некоторые абзимы, синтезированные таким способом, способны
направить на снижение активационного барьера целевой реакции почти
всю энергию сорбции субстрата. И хотя имеющиеся абзимы – не очень
мощные ферменты (они ускоряют спонтанную реакцию максимум в
105 раз, а не в 1010–1012 раз, как естественные ферменты, а кроме того в
абзимы ещё не умеют встраивать доноры и акцепторы электронов), – возможность их создания подтверждает важность преимущественного связывания именно переходного состояния.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Перечислите основные механизмы регуляции ферментативной активности.
2. Что такое аллостерия?
3. Что называется кооперативностью?
4. В чем отличие положительной кооперативности от отрицательной
кооперативности?
5. Как белок кальмодулин участвует в работе кальциевых белковых
переключателей?
6. Какую реакцию катализируют ферменты ГТФазы? В каких клеточных процессах участвуют ГТФазы?
7. Какие белки управляют активностью ГТФаз?
8. Какие ферменты участвуют в работе киназно-фосфотазных белковых переключателей?
9. Что такое протеолитическое разрезание? Как протеолитическое
разрезание может управлять ферментативной активностью?
10. Какие взаимодействия играют главную роль при связывании субстрата в активном центре фермента?
167
11. В чем сходство и различие моделей фермент-субстратного связывания "ключ-замок" и "рука-перчатка"?
12. За счёт каких факторов происходит ускорение ферментативной
реакции в модели сближения и ориентации?
13. За счёт каких факторов происходит ускорение ферментативной
реакции в модели индуцированного соответствия?
14. За счёт каких факторов происходит ускорение ферментативной
реакции в модели "дыбы"?
15. Какую роль играет (на что расходуется) потенциальная свободная
энергия связывания (сорбции) субстрата в активном центре фермента?
16. Какой процесс является источником энергии для понижения
барьера свободной энергии активации в ферментативной реакции?
17. Что такое антиген? Что такое эпитоп антигена?
18. Из каких компонентов состоит молекула антитела?
19. Как устроен антиген-связывающий карман антитела?
20. Как происходит отбор и подгонка антител под ксенобиотики?
21. Что такое моноклональные антитела?
22. За счёт чего абзимы катализируют биохимические реакции?
Активный центр в субъединице лактатдегидрогеназы схематически
показан на рисунке 98. При этом пептидный остов белка изображен в виде
ленты, дополнительно представлены молекулы: субстрата – лактата, ко-
фермента НАД⊕ и три боковые цепи аминокислот, которые участвуют
непосредственно в катализе.
Глава 8
ПРИМЕРЫ ФЕРМЕНТАТИВНЫХ ПРОЦЕССОВ
8.1. КАТАЛИТИЧЕСКИЙ ЦИКЛ ЛАКТАТДЕГИДРОГЕНАЗЫ
Активной формой фермента лактатдегидрогеназа (ЕС 1.1.1.27) является тетрамер из четырех субъединиц. Каждая субъединица образована
пептидной цепью из 334 аминокислот (36 кДа). В тетрамере субъединицы
занимают эквивалентные положения; каждый мономер содержит активный центр.
Кроме того, выделена пептидная петля, образованная аминокислотными остатками 98-111. В отсутствие субстрата и кофермента эта
структура раскрыта, что обеспечивает свободный доступ к субстратсвя-
168
169
Рисунок 98 – Схема тетрамера лактатдегидрогеназы и её активного центра
зывающему участку. На рисунке представлен блокированный активный
центр в тройном комплексе фермент-лактат-НАД⊕.
Механизм действия лактатдегидрогеназы можно представить в виде каталитического цикла.
Лактатдегидрогеназа катализирует передачу восстановительного
эквивалента от лактата на НАД⊕ (NАD+) или от НАДН (NADH) на пируват
L-лактат + NAD+ ↔ пируват + NADH + H+.
Каталитический цикл лактатдегидрогеназы представлен на рисунке 99 в виде шести моментальных "снимков". Приведенные на схеме промежуточные стадии катализа очень кратковременны и поэтому строго не
доказаны. Однако их существование подтверждается множеством экспериментальных данных.
В активном центре лактатдегидрогеназы принимают участие многие аминокислотные остатки. Они способствуют присоединению субстратов и кофермента или непосредственно участвуют в одной из стадий
катализа.
На рисунке 99 показаны только три особенно важные боковые цепи
аминокислот:
• положительно заряженная гуанидиновая группа аргинина-171
связывает карбоксильную группу субстрата с помощью электростатического взаимодействия,
• имидазольная группа гистидина-195 принимает участие в кислотно-основном катализе,
• боковая цепь аргинина-109 важна для стабилизации переходного состояния.
В противоположность His-195, меняющему свой заряд во время катализа, оба упомянутых остатка аргинина протонированы постоянно.
Рисунок 99 – Лактатдегидрогеназа: каталитический цикл
170
171
Кроме этих трех остатков (Arg-109, Arg-171 и His-195) важную роль
играет пептидная петля 98-111, показанная схематически на рисунке 99.
её функция состоит в том, чтобы после связывания субстрата и кофермента закрыть активный центр и исключить доступ молекул воды во время
переноса электронов.
Рассмотрим теперь отдельные стадии катализируемого лактатдегидрогеназой восстановления пирувата: в свободном ферменте (рису-
8.2. РАСЩЕПЛЕНИЕ АЦЕТИЛХОЛИНА АЦЕТИЛХОЛИНЭСТЕРАЗОЙ
Ацетилхолин является нейромедиатором в нервно-мышечных синапсах позвоночных. Его структурная формула имеет вид
нок 99(1)). His-195 протонирован (обозначен символом ⊕). Кофермент
NADH связывается первым (рисунок 99(2)), а за ним – пируват (рисунок 99(3)). Важно, что в молекуле фермента карбонильная группа пирувата и никотинамидное кольцо кофермента в активированном состоянии
расположены друг относительно друга оптимально и такая ориентация
фиксирована (сближение и ориентирование субстратов).
Затем закрывается петля 98-111 над активным центром. Сильно пониженная полярность в области активного центра облегчает образование
переходного состояния (рисунок 99(4); доступ воды закрыт).
В переходном состоянии гидрид-ион H– переносится с кофермента
на карбонильный углерод (перенос группы). При этом временно образующийся энергетически невыгодный отрицательный заряд на кислороде
стабилизируется электростатическим взаимодействием с Arg-109 (стабилизация переходного состояния).
Одновременно осуществляется перенос протона с Нis-195 на атом
кислорода (перенос группы), приводя к образованию связанных с ферментом лактата и NAD+ (рисунок 99(5)). После открытия петли лактат диссоциирует с фермента и временно незаряженная имидазольная группа Нis195 снова присоединяет протон из окружающей воды (рисунок 99(6)).
Наконец, освобождается также окисленный кофермент NAD+ и снова достигается исходное состояние (рисунок 99(1)).
При окислении лактата в пируват протекают то же стадии, но в противоположном направлении. Входящий в уравнение реакции протон присоединяется не одновременно с NADH а после освобождения лактата, т.е.
между стадиями (5) и (6) предшествующего цикла.
Субстрат ацетилхолинэстеразы ацетилхолин связывается в активном центре определенным образом за счет образования ионной связи ме-
172
173
Активный центр фермента ацетилхолинэстераза (ЕС 3.1.1.7) состоит из двух функционально важных и пространственно разделенных мест:
1) связывающей области, куда входит СОО-группа, электростатически взаимодействующая с положительно заряженным азотом N+
субстрата;
2) каталитической области, ответственной за эстеразную активность фермента, в которую входят Ser, His, Tyr (рисунок 100(а)).
а
б
в
Рисунок 100 – Схема расщепления ацетилхолина ацетилхолинэстеразой
жду отрицательно заряженной СОО–-группой и положительно заряженным четвертичным атомом азота N+ субстрата.
В начале реакции ферментативного гидролиза ацетилхолина на холин и уксусную кислоту
протон гидроксильной группы тирозина активного центра связывается с
атомом кислорода ацетилхолина (будущая спиртовая группа продукта
реакции – холина), а протон-кислородная связь серина "растягивается" и
серин "активизируется" гистидином (рисунок 100(б)).
В результате увеличивается положительный заряд на углеродном
атоме ацетильной группы субстрата, который атакуется отрицательно заряженным кислородным атомом белка, появившемся в результате диссоциации спиртовой группы серина активного центра. Связь между С
(ацетила) и О (холина) разрывается с образованием в качестве промежуточного соединения ацетилсерина. Отщепляющийся от серина протон
связывается кислородным атомом диссоциированной гидроксильной
группы тирозина, и первоначальное состояние тирозина в активном центре восстанавливается.
Гидролиз ацетилсерина начинается с диссоциации молекулы воды за
счет взаимодействия протона с имидазольным кольцом гистидина активного центра. Освободившийся гидроксил атакует сложноэфирную связь
ацетилсерина. Результатом гидролиза является освобождение уксусной
кислоты.
Н+, временно связанный с азотом имидазольной группы His, освобождается и вновь связывается с О Ser. Так восстанавливается исходное
состояние всех трех аминокислотных остатков активного центра.
Образовавшиеся холин и уксусная кислота освобождаются из активного центра за счет диффузии (рисунок 100(в)). Все описанные выше
процессы протекают более или менее одновременно. Гидролиз ацетилхо174
лина происходит благодаря согласованному действию всех функциональных групп активного центра. Течение реакции определяется расстояниями между отдельными участками активного центра.
Модельные опыты, проведенные с аналогами субстратов, показывают, что реакция протекает наиболее благоприятно, если основная группа гистидина находится на расстоянии 0,5 нм от СОО– и если тирозин
расположен в 0,25 нм от боковой цепи серина. Это ещё раз доказывает
важность конформации активного центра для проявления активности.
Ацетилхолинэстераза локализована в синаптической щели, её молекулярная масса – 260000 Да, субъединичная структура – α 2β 2 Фермент характеризуется поразительно высоким числом оборотов, а
именно 25000 с–1. Это означает, что одна молекула ацетилхолина расщепляется за 40 мкс. Такое высокое число оборотов ацетилхолинэстеразы имеет очень важное значение для быстрого восстановления
поляризованного состояния постсинаптической мембраны. Синапсы
способны передавать тысячу импульсов в секунду только потому, что
постсинаптическая мембрана восстанавливает свою поляризованность
за доли миллисекунды.
8.3. РАСЩЕПЛЕНИЕ ПОЛИПЕПТИДНЫХ ЦЕПЕЙ СЕРИНОВЫМИ
ПРОТЕАЗАМИ
Сериновые протеазы разрезают полипептидные цепи, т.е. проводят
реакцию
Реакция гидролиза пептидной цепи, когда в среде достаточно много
воды, идет самопроизвольно, но очень медленно, за многие годы, – то есть
гидролиз (при наличии свободной воды) термодинамически выгоден, но
175
требует преодоления очень высокого активационного барьера. Если же
свободной воды в среде нет, то реакция идет в обратную сторону, в сторону синтеза полипептида и выделения воды (тоже очень медленно).
Ферментативная реакция гидролиза пептида (или, при отсутствии
свободной воды, реакции его синтеза из более мелких фрагментов) занимает доли секунды – фермент резко снижает активационный барьер реакции. Общий ход реакции показан на рисунке 101.
Фермент схематически изображен в виде прямоугольника, активация серина гистидином показана стрелкой, а на субстрате показан только
боковой радикал R той аминокислоты, которая определяет специфичность
фермент-субстратного связывания (рисунок 101(а)).
Активный центр сериновых протеаз включает в себя собственно
каталитический центр и субстрат-связывающий центр.
Катализ в сериновых протеазах непосредственно осуществляется
боковой цепью серина (в цепи химотрипсина это Ser195). Для того чтобы
серин мог катализировать гидролиз, его (серин) нужно активизировать.
Пока кислород находится в форме –ОН группы, он не активен, а активным он становится после утери Н+ и перехода в форму –О–. Этим отрывом протона от Ser195 занимаются два остальных члена "триады
переноса заряда" – His57 (он и принимает протон) и "вспомогательный"
Asp102. Любые замены этих трех аминокислот методами точечного мутагенеза прекращают каталитическую активность трипсиновых протеаз.
Реакция начинается со связывания N-концевой части субстрата в
активном центре фермента, при этом нарушается плоская топология разрываемой пептидной связи, избыточный отрицательный заряд скапливается на на кислороде группы С=О, атом С этой группы тетраэдризуется
(рисунок 101(б), тетраэдрическое переходное состояние первого этапа
ферментативной реакции). Протон активированной гидроксильной группы серина (находящийся уже на гистидине) переходит с донора His+ на N
(азот) С-части пептида. Пептидная связь рвется, С-концевой пептид выходит из активного центра, N-концевой пептид временно (но ковалентно)
связывается с кислородом серина (рисунок 101(в)). Затем в активный
центр входит молекула воды и под действием имидазольной группы гис-
тидина и С=О группы N-концевого пептида диссоциирует на протон Н+ и
ОН-группу (рисунок 101(г)).
176
177
а
б
в
г
д
е
Рисунок 101 – Схема ферментативного гидролиза пептида. Цифрами обозначены: 1 – оксианионовая дыра; 2 – специфический субстрат-связывающий карман;
3 – неспецифическая пептид-связывающая площадка
Гидроксильная группа присоединяется к С=О группе N-концевого
пептида, связанного с серином фермента, формируя "заготовку" СООН
группы на конце этого пептида (рисунок 101(д), тетраэдрическое переходное состояние второго этапа ферментативной реакции), а Н+ протонирует гистидин. Этот протонированный гистидин His+ затем становится
донором протона для серина.
Переход протона с гистидина на серин разрывает связь N-концевого
пептида с ферментом. N-концевой пептид выходит из активного центра, а
ОН-группа серина снова остается активированной гистидином (активация
показана стрелкой на рисунке 101(е)). Фермент вернулся в исходное
состояние.
Субстрат-связывающий центр состоит из (рисунок 101):
1) оксианионовой дыры, связывающей кислород расщепляемой
пептидной группы,
2) специфического субстрат-связывающего кармана, отвечающего
за распознавание той аминокислоты, по карбоксилу которой
производится расщепление пептида,
3) неспецифической пептид-связывающей площадки, обеспечивающей вместе с оксианионовой дырой правильную пространственную ориентацию расщепляемой пептидной группы относительно активированного О-атома боковой группы Ser195.
Схема, которая изображена на рисунке 101, и которая иллюстрирует
ход реакции гидролиза пептидной цепи сериновыми протеазами, была получена в результате многолетних исследований многих групп. Для её построения привлекались данные различных исследований, в частности:
(1) данные по катализу разных субстратов;
(2) данные по химическим модификациям фермента;
(3) данные сайт-специфического мутагенеза (которые показали,
какие аминокислоты фермента вовлечены в катализ);
(4) исследования ферментов в комплексе с конкурентными ингибиторами;
178
(5) рентгеноструктурные работы (определившие места образования водородных связей).
Для анализа ферментативной реакции (рисунок 101) сравним её с
аналогичной неферментативной самопроизвольной реакцией, протекающей в водном растворе (рисунок 102).
Рисунок 102 – Схема неферментативного гидролиза пептида в конгруэнтной
системе
Такого рода модельная система, в которой химические преобразования проходят через те же промежуточные соединения, что и в ферментативной реакции называется конгруэнтной.
Ферментативная реакция идет в две стадии:
1) сначала отщепляется С-концевой пептид и образуется комплекс N-концевого пептида с О-атомом серина (рисунок 101(б)),
2) затем этот N-пептид заменяет свою связь с О-атомом серина на связь с О-атомом воды (рисунок 101(д)).
А без фермента реакция идет в одну стадию, в которой одновременно отщепляется С-концевой пептид и образуется комплекс
N-концевого пептида с О-атомом воды.
179
И ферментативная, и неферментативная реакции идут через тетраэдрический активированный комплекс (или тетраэдрическое переходное
состояние), точнее, через активированный комплекс, в котором рядом с
тетраэдрическим С-атомом находится донор протона (His+ в ферменте
или ион гидроксония ОН3+ в воде).
То, что на пути ферментативной реакции находится два активированных комплекса (а не один, как в неферментативной) – не может, само
по себе, ускорить реакцию. Однако ускоряет её то, что активированный
фермент-субстратный комплекс более стабилен (именно нестабильность
переходного состояния и лимитирует скорость реакции), чем активированный комплекс в воде.
Переходное состояние на ферменте стабилизируется следующим
образом.
Во-первых, отрицательный заряд атома О–, образующийся при тетраэдризации С-атома, на ферменте втягивается в оксианионовую дыру,
где расположены два протона. Связь с этими положительно заряженными
протонами понижает свободную энергию отрицательного заряда O– и,
следовательно, энергию тетраэдризации С-атома по сравнению с неферментативной реакцией, где такой "дыры" нет, то есть приводит к понижению энергии (энтальпии) переходного состояния или к так называемому энтальпийному катализу.
Во-вторых, рядом с тетраэдрическим С-атомом расположен донор
протона His+, который примерно столь же стабилен, как "безпротонный"
His0. В воде роль донора протона должен играть ион ОН3+, – ион, концентрация которого, вследствие его нестабильности, в воде крайне мала (порядка 10–7 моля на литр). Встреча такого иона с пептидом маловероятна,
"вылавливание" этого иона из воды понижает энтропию и соответственно
повышает свободную энергию активированного комплекса. Поэтому в
воде энтропия препятствует одновременному участию в реакции всех
компонентов активированного комплекса (снижает вероятность их встречи), но на ферменте такого энтропийного ограничения нет – все эти
компоненты уже собраны вместе в фермент-субстратном комплексе.
Снижение энтропии за счет "вылавливания" фермента субстратом ком-
пенсируется его сорбцией в субстрат-связывающем кармане. Этот облегченный сбор всех компонентов активированного комплекса понижает его
свободную энергию на ферменте по сравнению с неферментативной реакцией, и приводит к так называемому энтропийному катализу.
В сумме, энтропийная и энтальпийная компоненты катализа ускоряют ферментативную реакцию примерно в 1010 раз по сравнению с неферментативной.
Если фермент-субстратный комплекс достаточно прочный, а концентрация субстрата достаточно велика, то энтропийный катализ понижает наблюдаемый порядок реакции по концентрации субстрата. Теперь
её скорость зависит лишь от концентрации фермента, а от концентрации
субстрата (или субстратов) в растворе не зависит. Этот эффект особенно
силен тогда, когда речь идет о реакции, в которую вовлечено несколько
молекул-субстратов (мультисубстратные реакции), например, при синтезе
пептида из двух фрагментов в отсутствии воды.
180
181
8.4. СТРУКТУРНЫЕ ОСОБЕННОСТИ ФЕРМЕНТОВ
Ферментативный гидролиз пептидов сериновыми протеазами чрезвычайно специфичен. Так химотрипсин разрезает полипептид только
после ароматических аминокислот, трипсин – после положительно заряженных аминокислот, эластаза – только после самых маленьких (аланин). Этот эффект (проявление механизма "ключ–замок") достигается
специфической структурой той части субстрат-связывающего "кармана"
(рисунок 103), куда помещается последняя (как на трипсине) или предпоследняя (как на папаине) перед точкой разрезания боковая группа R
пептида.
В активном центре эластазы размеры сорбционной области, где
происходит связывание метильной группы субстрата, намного меньше,
чем у химотрипсина. Это вызвано тем, что два глицина (Gly216 и Gly226),
расположенные у входа в карман химотрипсина, в случае эластазы замещены более объемными валином (Val216) и треонином (Thr226) (рисунок 103(в)).
Если сравнить субстрат-связывающий центр химотрипсина с трипсином, то размеры и форма сорбционного участка в активных центрах
обоих ферментов примерно одинаковы. Единственное различие в первичной структуре полипептидных фрагментов, образующих гидрофобный
карман, состоит в том, что в химотрипсине остаток 189 – это серин
Ser189, а в трипсине в соответствующем положении находится отрицательно заряженная аспарагиновая кислота Asp189.
а
б
в
Рисунок 103 – Схема специфического сайта субстрат-связывающего кармана в
разных сериновых протеазах: а – химотрипсин; б – трипсин; в – эластаза
глобулы используется как некая инфраструктура, с достаточно произвольной и, в некоторых случаях, даже рыхлой, разупорядоченной структурой, служащая только для того, чтобы точно сформировать
каталитические и сорбционные участки – точно расположить в пространстве компоненты этих участков.
Поэтому оказывается, что белки с совсем разной первичной структурой, и даже с совсем разной третичной структурой могут иметь одинаковые или очень сходные биохимические функции. Сериновые протеазы
являются классическим примером такого структурного принципа сочетания стабильных глобулярных структур, в которых точность подгонки молекулярных фрагментов не задана жестко, с несколькими локальными
участками биомолекулы, в которых реализуется заданный высокий уровень точности пространственного позиционирования атомов.
Два класса сериновых протеаз – типа трипсина и типа субтилизина
– не похожи ни по аминокислотной последовательности, ни по общей
форме (рисунок 104), и даже принадлежат к разным структурным классам
(трипсин – двухдоменный β-белок, субтилизин – однодоменный
α/β-белок).
Это приводит к тому, что в отличие от химотрипсина трипсин обнаруживает специфичность к гидролизу пептидных связей, образованных
положительно заряженными аминокислотами (Lys, Arg). Сорбция положительно заряженного субстрата на ферменте (вблизи каталитически активного нуклеофила активного центра) происходит в данном случае за
счет электростатических взаимодействий.
Изучение ферментативной деятельности белков показывает, что активный центр фермента занимает небольшую часть белковой глобулы, в
то время как остальная её часть служит лишь как бы твердым каркасом,
обеспечивающим "правильное" строение закрепленного на нем активного
центра.
Ферменты оптимизированы эволюцией так, чтобы только в нескольких определенных критических местах их структуры атомы располагались в точных пространственных позициях. Остальной объем белковой
субтилизина. Схематически изображены α-спирали, β-листы и β-цилиндры. Район активного центра показан треугольником
182
183
а
б
Рисунок 104 – Схема строения сериновых протеаз: а – типа трипсина; б – типа
Трипсин и субтилизин имеют одинаковую конфигурацию лишь
ключевых аминокислотных остатков в каталитическом центре (рисунок 105), причем не всех остатков целиком, а лишь их функциональноважных радикалов, но не имеют одинаковой конфигурации аминокислотных остатков даже в субстрат-связывающем кармане.
На рисунке 105 показаны фрагменты главной цепи (направление
хода цепи в этих фрагментах обозначены черными стрелками); шарами
(с N внутри) показано положение оксианионовых дыр, в которые помещаются H–Nα-группа глицина (Gly193) главной цепи субстрата в трипсине (рисунок 103(а)) или H–Nδ-группа бокового радикала аспарагина
(Asn155) субстрата в субтилизине (рисунок (103(б)).
Видно, что только пространственное расположение концов боковых
групп каталитической триады переноса заряда (Ser, His, Asp) (и, возможно, положение оксианионовой дыры) подобны в этих двух классах сериновых протеаз, в то время как значительные отличия наблюдаются даже
в ходе главной цепи у ключевых каталитических остатков His и Asp.
Более того, существуют протеазы, совершенно не похожие на сериновые протеазы даже в зоне каталитического центра, например, металлопротеазы типа карбоксипептидаз (ЕС 3.4.17.n).
В карбоксипептидазах ключевую роль в катализе играет встроенный
в белок ион Zn2+. Имея маленькие радиусы, многозарядные металлические ионы создают вокруг себя очень сильное электрическое поле. Это
позволяет им в металлопротеазах активировать молекулу воды (отщепляя
от нее Н+) с тем, чтобы та осуществила бы далее разрыв пептидной связи
(подобно тому, как показано на рисунке 102), и, одновременно, стабилизировать зарядом Zn2+ отрицательный заряд на тетраэдрическом переходном состоянии разрываемого пептида.
Таким образом, одна и та же химическая реакция может осуществляться совершенно разными белками. При этом одну и ту же ключевую
каталитическую роль – роль мощных "электрических резаков" – в одних
белках играют многозарядные металлические ионы, в других – органические кофакторы, легко принимающие электроны или протоны, в третьих
– активированные своим окружением (как в трипсине) боковые группы.
8.5. ФЕРМЕНТАТИВНЫЕ РЕАКЦИИ ГЛИКОЛИЗА
а
б
Рисунок 105 – Схема строения каталитических центров сериновых протеаз:
а – типа трипсина, б – типа субтилизина
184
Гликолиз осуществляют десять водорастворимых цитозольных
ферментов, в результате чего одна молекула глюкозы конвертируется в
две молекулы пирувата (рисунок 106). Все промежуточные вещества между глюкозой и пируватом являются фосфорилированными соединениями. Реакции 1, 3 и 10 являются необратимыми при физиологических
условиях.
Глюкоза, которую ткани получают из крови, в клетке также предварительно активируется путем фосфорилирования. В АТФ-зависимой реакции, катализируемой гексокиназой (ЕС 2.7.1.1) (реакция 1) глюкоза
превращается в глюкозо-6-фосфат. После изомеризации глюкозо-6фосфата в фруктозо-6-фосфат ферментом фосфоглюкоизомераза (глюкозо-6-фосфат изомераза (ЕС 5.3.1.9)) (реакция 2) последний вновь фосфорилируется с образованием фруктозо-1,6-бисфосфата.
185
Фосфофруктокиназа (ЕС 2.7.1.11), катализирующая эту стадию 3,
является важным ключевым ферментом гликолиза.
Рисунок 106 – Последовательность реакций гликолиза
186
До этого момента на одну молекулу глюкозы расходуются две молекулы АТФ. Фруктозо-1,6-бисфосфат расщепляется далее альдолазой
(ЕС 4.1.2.13) (реакция 4) на два фосфорилированных С3-фрагмента. Эти
фрагменты – глицеральдегид-3-фосфат и дигидроксиацетонфосфат – превращаются один в другой триозофосфатизомеразой (ЕС 5.3.1.1) (реакция 5) (рисунки 79, 80). Глицеральдегид-3-фосфат затем окисляется
глицеральдегид-З-фосфатдегидрогеназой (EC 1.2.1.12) (реакция 6) с образованием НАДН + Н+. В этой реакции в молекулу включается неорганический фосфат (так называемое "субстратное фосфорилирование") с
образованием 1,3-дифосфоглицерата.
Субстратным фосфорилированием называется перенос неорганического фосфата Pi на АДФ за счет высокого химического потенциала
(а не за счет окислительного фосфорилирования с использованием градиента электрохимического потенциала на биомембране). Такие процессы
потому и называются субстратным фосфорилированием, поскольку они
являются частью метаболического пути ("субстратной цепи").
Субстратное фосфорилирование реализуется только в двух реакциях – в реакции гликолиза и в реакции образования ГТФ в цитратном
цикле (цикле Кребса).
Промежуточное соединение 1,3-дифосфоглицерат содержит смешанную ангидридную связь, расщепление которой является высоко экзергоническим процессом. На следующей стадии 7 (катализируемой фосфоглицераткиназой (ЕС 2.7.2.3)) гидролиз этого соединения сопряжен с
образованием АТФ.
Следующий промежуточный продукт, гидролиз которого может
быть сопряжен с синтезом АТФ, образуется в реакции изомеризации
3-фосфоглицерата (полученного в результате реакции 7) в 2-фосфоглицерат в реакции 8 (фермент: фосфоглицератмутаза (ЕС 2.4.5.1)) и
последующего отщепления воды (реакция 9, фермент: енолаза (или фосфопируватгидратаза (ЕС 4.2.1.11))). Продукт представляет собой сложный эфир фосфорной кислоты и енольной формы пирувата и потому
называется фосфоенолпируватом (PEP). На последней стадии 10, которая
катализируется пируваткиназой (EС 2.7.1.40), образуются пируват и АТФ.
187
Наряду со стадией 6 и тиокиназной реакцией в цитратном цикле это третья реакция, позволяющая клеткам синтезировать АТФ независимо от
дыхательной цепи. Несмотря на образование АТФ она высоко экзергонична и потому необратима.
В ходе гликолиза синтезируется четыре молекулы АТФ в ходе
ферментативных реакций 7 и 10 (в которых, в отличие от синтеза АТФ в
митохондриях и хлоропластах, не используется протондвижущая сила).
При этом в реакциях 1 и 3 расходуется две молекулы АТФ. В результате
гликолиз одной молекулы глюкозы дает только две молекулы АТФ.
Чтобы точно уравнять реакцию гликолиза в правой части уравнения
следует учесть ещё четыре атома водорода (точнее, четыре протона и четыре электрона)
C6H12O6 → 2 CH3(CO)2COOH + 4 H+ + 4 e–.
Все четыре электрона и два из четырех протонов переносятся на две
молекулы электронного переносчика никотинамидадениндинуклеотида в
его окисленной форме НАД⊕, образуя их восстановленную форму НАДН
2 H+ + 4 e– +2 НАД⊕ → 2 НАДН.
Реакция 6, в которой образуются эти водородные атомы и переносятся на НАД+ катализируется ферментом глицеральдегид-3-фосфатдегидрогеназа. Полное уравнение гликолиза имеет вид
С6H12O6 + 2 НАД⊕ + 2 Pi2– + 2 АДФ3– → 2 C3Н4O3 + 2 НАДН + 2 АТФ4–.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какие компоненты полипептидной цепи формируют активный
центр фермента лактатдегидрогеназа?
2. Какую реакцию катализирует фермент лактатдегидрогеназа?
3. Какую функцию выполняет НАДН в каталитическом цикле
лактатдегидрогеназы?
4. Какую биологическую роль выполняет ацетилхолин?
188
5. Какие компоненты полипептидной цепи формируют активный
центр фермента ацетилхолинэстераза?
6. Какую реакцию катализирует фермент ацетилхолинэстераза?
7. Какую функцию выполняет аминокислота серин в каталитической
реакции расщепления ацетилхолина ацетилхолинэстеразой?
8. Какую реакцию катализируют сериновые протеазы?
9. Какие компоненты полипептидной цепи формируют активный
центр сериновых протеаз?
10. Как устроен субстрат-связывающий центр сериновой протеазы?
11. Чем отличается ферментативная реакция расщепления полипептидной цепи сериновой протеазой от аналогичной неферментативной реакции?
12. Какие особенности ферментативной реакции расщепления полипептидной цепи сериновой протеазой обеспечивает энтальпийный
катализ? И какие – энтропийный катализ?
13. Чем отличаются специфические сайты субстрат-связывающего
кармана в химотрипсине, трипсине и эластазе?
14. Для чего в катализаторах совмещается локальная точность расположения отдельных аминокислот с достаточно произвольной
структурой основной части белковой глобулы?
15. В состоянии ли ферменты, которые имеют полностью различную
первичную структуру, катализировать подобные реакции?
16. В состоянии ли белки, которые имеют различную третичную
структуру выполнять подобные биохимические функции?
17. Сколько ферментов принимает участие в гликолизе?
18. Образуются ли во время гликолиза нефосфорилированные
вещества?
19. Что такое субстратное фосфорилирование?
20. Сколько молекул АТФ синтезируется при гликолизе одной молекулы глюкозы?
189
РАЗДЕЛ III
КИНЕТИКА ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
Главный признак, отличающий живое от неживого, это движение,
постоянное развитие во времени. Особенности протекания во времени метаболических процессов в живых организмах представляют собой сложную суперпозицию индивидуальных кинетических характеристик тех
ферментов, которые входят в состав определенных метаболических цепей. Исследование количественных закономерностей развития биохимических процессов на молекулярном уровне во времени с участием
ферментов составляет предмет ферментативной кинетики. Среди задач
ферментативной кинетики главными являются выяснение механизмов,
определяющих скорости и природу ферментативных преобразований, выявление их лимитирующих стадий, количественное описание протекания
ферментативных реакций во времени с использованием молекулярных
представлений и базовых законов физической и химической кинетики.
Глава 9
ОСНОВЫ ФОРМАЛЬНОЙ КИНЕТИКИ
9.1. ОСОБЕННОСТЬ ФЕРМЕНТАТИВНОЙ КИНЕТИКИ
Основные трудности при исследовании ферментативных процессов
сопряжены не с их экспериментальным изучением (что часто имеет место), а с аналитическим выражением получаемых результатов.
190
Иногда аналитическое выражение имеет настолько сложный вид,
что это не позволяет объяснить исследуемый процесс.
Упрощенные схемы ферментативной кинетики служат одним из
лучших примеров того, как с помощью обоснованных приближений можно свести сложную задачу к понятному и решаемому варианту.
Кинетика химических реакций с участием ферментов принципиально отличается от обычных химических реакций.
Скорость большинства химических реакций пропорциональна концентрации реагентов в системе. Например, для реакции
A + B → Продукты
выражение для скорости реакции имеет вид
w=
d[ A] d[ B ]
=
= k[ A][ B ] .
dt
dt
В отличие от обычных химических реакций, скорости ферментативных реакций часто не зависят от концентрации субстрата.
Простое объяснение этого факта состоит в том, что для успешного
протекания реакции требуется образование фермент-субстратного комплекса; и при достаточно высокой концентрации субстрата фермент будет
"насыщен", так что практически весь фермент в любой данный момент
времени связан с субстратом.
Следовательно, скорость суммарного химического процесса достигнет максимально возможного значения, пропорционального концентрации фермента в системе, но независящего от концентрации
(избыточной) субстрата.
Рассмотрим простейшую бисубстратную ферментативную реакцию
A+ B+ E ↔ E + P+Q,
где A и B – два субстрата; P и Q – продукты; E – свободный фермент.
Общей моделью в этом случае будет схема, представленная на рисунке 107.
191
EA , EB , EAB , EPQ , EP и EQ – обозначают на рисунке 107 раз-
ные возможные комплексы фермента с субстратом (субстратами) и продуктом (продуктами). Математические выражения, описывающие эту
модель не пригодны ни для каких практических целей.
EP + Q
EA + B
A+ B+ E
E+ P+Q
EPQ
EAB
k1
k2
k−1
k−2
E + S → ES → E + P ,
← ←
где k1, k2 , k−1, k−2 – константы скоростей соответствующих реакций.
3. Третье упрощение. Ограничим период наблюдений только начальным этапом реакции до тех пор, пока не накопилось значительное количество продукта.
При этом можно не учитывать обратную реакцию между E и P ,
приводящую к образованию ES
k1
EB + A
EQ + P
Рисунок 107 – Общая схема бисубстратной ферментативной реакции
Михаэлис и Ментен предложили оригинальный подход, который в
рамках стационарной кинетики позволил существенным образом упростить описание кинетики ферментативных реакций.
9.2. ГИПОТЕЗА О СТАЦИОНАРНОСТИ
Покажем теперь, как Михаэлис и Ментен с помощью разумных упрощений получили кинетическую схему, пригодную для анализа огромного числа ферментативных реакций.
1. Первое упрощение. Считаем, что в реакции участвует только
один субстрат S , с которым взаимодействует фермент E .
Тогда останется схема
E + S ↔ ES ↔ EP ↔ E + P .
k2
E + S → ES → E + P .
←
k−1
4. Четвертое упрощение. Считаем, что концентрация фермента мала по сравнению с (начальной) концентрацией субстрата (избыток субстрата) и по сравнению с равновесной концентрацией продукта
[ E ]0 [ S ]0 .
Это предположение необходимо, чтобы сохранять концентрацию
фермент-субстратного комплекса постоянной, то есть для того, чтобы
состояние системы можно было рассматривать как стационарное.
Именно это, последнее, допущение о стационарном состоянии является самым "сильным" и необходимым для описания ферментативной
кинетики в сжатом виде.
Для того чтобы проанализировать процесс
k1
k2
E + S → ES → E + P ,
←
k−1
2. Второе упрощение. Считаем, что в реакции образуется только
одно промежуточное соединение. В этом случае кинетическую схему
процесса можно записать в виде
мы в последующих параграфах предварительно рассмотрим последовательно усложняемую формальную кинетическую схему.
192
193
9.3. ОДНОСТАДИЙНАЯ ОДНОКОМПОНЕНТНАЯ ПРЯМАЯ РЕАКЦИЯ
Рассмотрим простейший случай – одностадийную однокомпонентную прямую реакцию
где [ A]0 – концентрация вещества A в начальный момент времени t = 0 ;
[ A] – концентрация в момент времени t .
Графические зависимости концентрации реагентов от времени (кинетические кривые) представлены на рисунке 108.
k1
A→ B ,
для которой очевидно [ B ] = 1 − [ A] , и которая характеризуется скоростью
[A]0
[B] = 1 – [A]
исчезновения реагента A
d[ A]
= −k1[ A] .
dt
Для того чтобы решить это дифференциальное уравнение, разделяем переменные
k1 d t = −
[A]
0
Время, t
Рисунок 108 – Кинетические кривые одностадийной однокомпонентной прямой
реакции
d[ A]
[ A]
9.4. ПРЯМАЯ И ОБРАТНАЯ РЕАКЦИИ
и интегрируем части в пределах (0, t ) и ([ A]0 ,[ A]) соответственно
t
[ A]
0
[ A]0
∫ k1 d t = − ∫
d[ A]
,
[ A]
Двусторонней (обратимой) элементарной реакцией первого порядка
называется реакция, состоящая из прямой и обратной элементарных реакций первого порядка,
k1
k1t = −(ln[ A] − ln[ A]0 ) ,
A →← B ,
[ A]
k1t = ln 0 .
[ A]
где k1 и k −1 – константы скорости соответственно прямой и обратной
k−1
элементарных стадий. (Пример – реакция изомеризации).
Откуда получаем выражения для расчета константы скорости химической реакции и концентрации реагирующего вещества в любой момент
времени
1 [ A]
k1 = ln 0 ,
t [ A]
[ A] = [ A]0 exp(− k1t ),
194
k1
Для реакции A →← B уменьшение концентрации x = [ A]0 − [ A] вещеk−1
ства A равно увеличению концентрации x = [ B] − [ B]0 вещества B к моменту времени t . Следовательно
w=
1 d[ A] d x
=
.
(−1) d t
dt
195
Поскольку
dA
= −k1[ A] + k−1[ A] и [ A] = [ A]0 − x , [ B] = [ B]0 + x , то
dt
Разделяем переменные
dx
= (k1 + k−1 )d t
x∞ − x
dx
= k1 ([ A]0 − x) − k −1 ([ B ]0 + x) .
dt
и интегрируем
k1
→
←
k−1
При достаточно долгом t → ∞ протекании реакции A B наступа-
t
ет состояние равновесия, в котором x = x∞ = const . При этом скорость
прямой реакции равна скорости обратной реакции, соответственно скорость двусторонней реакции равна нулю
dx
dt
x
(k1 + k−1 )t = − ln( x∞ − x) 0 = − ln( x∞ − x) − (− ln x∞ ) = ln
= 0 . Следовательно
[ B ]0 + x∞ k1
=
.
[ A]0 − x∞ k−1
При этом
x∞
,
x∞ − x
x∞ − x
= exp[−(k1 + k−1 )t ] ,
x∞
k1 ([ A]0 − x∞ ) − k−1 ([ B]0 + x∞ ) = 0 ,
K=
dx
,
x −x
0 ∞
0
x = x∞
и состояние равновесие можно охарактеризовать константой равновесия
x
∫ (k1 + k−1)d t = ∫
x = x∞ (1 − exp[−(k1 + k−1 )t ]) .
Соответственно, получаем
[ A] = [ A]0 − x = [ A]0 − x∞ (1 − exp[−(k1 + k−1 )t ]) ,
[ B] = [ B]0 + x = [ B]0 + x∞ (1 − exp[−(k1 + k−1 )t ]) .
Для случая [ B]0 = 0 , т. е. в том случае, когда в начале реакции про-
x∞ =
Решим кинетическое уравнение
k1[ A]0 − k−1[ B ]0
.
k1 + k−1
dx
= k1 ([ A]0 − x) − k−1 ([ B]0 + x) :
dt
dx
= k1 ([ A]0 − x) − k−1 ([ B]0 + x) =
dt
= (k1[ A]0 − k−1[ B]0 ) − (k1 + k−1 ) x =
⎛ (k [ A] − k [ B] )
⎞
= (k1 + k−1 ) ⎜ 1 0 −1 0 − x ⎟ =
(k1 + k−1 )
⎝
⎠
дукта в системе нет, решения будут иметь вид
[ A] = [ A]0 −
[ B] =
k1[ A]0
(1 − exp[−(k1 + k−1 )t ]) ,
k1 + k−1
k1[ A]0
(1 − exp[−(k1 + k−1 )t ]).
k1 + k−1
Из-за обратной реакции [ A] не падает до нуля; конечные предельные концентрации A и B достигаются быстрее, чем в случае одностадийной однокомпонентной прямой реакции, который был рассмотрен ранее.
= (k1 + k−1 )( x∞ − x).
196
197
Зависимость концентрации исходного вещества [ A] и продукта ре-
d[ A]
= −k1[ A],
dt
d[ B ]
= k1[ A] − k2 [ B],
dt
d[ P ]
= k2[ B ].
dt
k1
акции [ B] от времени t для обратимой реакции первого порядка A →
←B
k−1
Концентрация
для случаев K > 1 и K < 1 представлена на рисунке 109.
A⇔B
K>1
k1>k–1
[A]
K<1
k1<k–1
Как было показано выше, решение первого уравнения системы имеет вид
[ A] = [ A]0 exp(− k1t ) .
[A]
x∞
Подставим это выражение во второе уравнение системы и получим
[B]
[B]
d[ B]
= k1[ A]0 exp(−k1t ) − k2 [ B] .
dt
x∞
Время, t
Время, t
Решение этого уравнения (без доказательства) имеет вид
[ B] =
Рисунок 109 – Зависимость концентрации исходного вещества и продукта реакции от времени (кинетические кривые) для обратимой реакции первого порядка
k1
k1
Заметим, что реакция A → B и реакция A→ B практически заканчи←
k−1
ваются прежде, чем концентрация какого-либо реагента станет постоянной.
9.5. ПОСЛЕДОВАТЕЛЬНЫЕ РЕАКЦИИ
Рассмотрим гомогенную реакцию в закрытой системе с двумя односторонними мономолекулярными элементарными стадиями
k1
k2
Проверим, так ли это, подставим это решение во второе уравнение системы и сократим k1[ A]0
[ A]0
k1
( −k1 exp(−k1t ) + k2 exp(−k2t ) ) =
k2 − k1
= k1[ A]0 exp(− k1t ) − k2 [ A]0
198
k1
( exp(−k1t ) − exp(−k2t ) ) ,
k2 − k1
1
( −k1 exp(−k1t ) + k2 exp(−k2t ) + k2 exp(−k1t ) − k2 exp(−k2t ) ) = exp(−k1t ) ,
k2 − k1
1
( k2 exp(−k1t ) − k1 exp(−k1t ) ) = exp(−k1t ) – получили тождество.
k2 − k1
Подставим [ B] =
A→ B → P .
В этом случае, для описания этой модели потребуется решить систему кинетических уравнений
k1[ A]0
( exp(−k1t ) − exp(−k2t ) ) .
k2 − k1
ния системы) в
k1[ A]0
( exp(−k1t ) − exp(−k2t ) ) (решение второго уравнеk2 − k1
d[ P ]
= k2[ B ] (третье уравнение системы)
dt
d[ P] k2 k1[ A]0
=
( exp(−k1t ) − exp(−k2t ) ) .
dt
k2 − k1
199
Полученное уравнение решим, используя соотношение материального баланса
Таким образом, в процессе существует момент времени, в который
концентрация промежуточного соединения B начинает уменьшаться.
[ A]0 − [ A] = [ B] + [ P] или [ P] = [ A]0 − [ A] − [ B] .
9.6. НЕКАТАЛИЗИРУЕМАЯ РЕАКЦИЯ С ОДНИМ ПРОМЕЖУТОЧНЫМ
СОЕДИНЕНИЕМ
Подставляем в [ P] = [ A]0 − [ A] − [ B ] выражения [ A] = [ A]0 exp(−k1t ) и
[ B] = [ A]0
k1
( exp(−k1t ) − exp(−k2t ) ) . В результате получаем
k2 − k1
Рассмотрим некатализируемую реакцию с одним промежуточным
соединением
k1
⎛
⎞
k1
k1
[ P] = [ A]0 ⎜1 − exp(−k1t ) −
exp(−k1t ) +
exp(−k2t ) ⎟ ,
k
k
k
k
−
−
⎝
⎠
2
1
2
1
⎛
⎞
k2
k1
[ P] = [ A]0 ⎜1 −
exp(− k1t ) +
exp(−k2t ) ⎟ .
k2 − k1
⎝ k2 − k1
⎠
На рисунке 110 приведены кинетические кривые в безразмерных
⎛ [X ]
⎞
координатах ⎜
, k1t ⎟ для случая k1 = 2k 2 , где X = A, B, P .
⎝ [ A]0
⎠
[A]
0
k−1
Схема этой реакции уже напоминает схему ферментативной реакции
k1
k2
E + S → ES → E + P
←
k−1
с тем отличием, что при завершении реакции реагент B не регенерируется.
Система кинетических уравнений для этой реакции:
d[ A]
d[ B]
,
= −k1[ A][ B ] + k−1[ X ] =
dt
dt
d[ X ]
= k1[ A][ B ] − k−1[ X ] − k2 [ X ],
dt
d[ P ]
= k2 [ X ],
dt
k 1 =2k 2
[P]
и уравнение материального баланса
[X]/[А]0
Относительная концентрация
1
k2
A + B→ X → P .
←
k1
[ P] = [ A]0 − [ A]0 exp(−k1t ) − [ A]0
( exp(−k1t ) − exp(−k2t ) ) ,
k2 − k1
[ A] 0 − [ A] = [ B] 0 − [ B] .
[B ]
Для системы четырех независимых уравнений с четырьмя неизвестными [ A],[ B],[ X ],[ P] решение существует, но его невозможно аналитиче0
1
2
3
k 1t
4
ски выразить для всех случаев. Типичный ход кинетических кривых для
случая k1 ≈ k −1 ≈ k 2 и [ A]0 ≈ [ B]0 приведен на рисунке 111.
Рисунок 110 – Кинетические кривые последовательной реакции
200
201
и уравнение материального баланса
[A]0
[B]0
[P]
[A]
[B]
[X]
0
Время, t
Рисунок 111 – Кинетические кривые для случая некатализируемой реакции с
одним промежуточным соединением
9.7. КАТАЛИТИЧЕСКАЯ РЕАКЦИЯ С ОДНИМ ПРОМЕЖУТОЧНЫМ
[ E ] 0 = [ E ] + [ ES ]
полностью описывают кинетическое поведение системы.
Хотя общего решения этой системы не существует, компьютерное
моделирование позволяет строить кинетические кривые для частных случаев.
На рисунке 112(а) приведены кинетические кривые для случая
k1 ≈ k −1 ≈ k 2 и [ S ]0 [ E ]0
Концентрация
[S]0
[P]
СОЕДИНЕНИЕМ
k1
k2
E + S → ES → E + P .
←
a
[S]
k−1
[ES]
Это уравнение описывает кинетическую схему ферментативной
реакции фермента E и субстрата S с образованием продукта реакции P .
Эта схема обычно служит отправной точкой в кинетике ферментативных реакций и отличается от предыдущего случая только тем, что в
конце реакции фермент (катализатор) регенерируется.
Система кинетических уравнений
d[ S ]
= − k1[ S ][ E ] + k−1[ ES ],
dt
d[ ES ]
= k1[ S ][ E ] − k−1[ ES ] − k2[ ES ],
dt
d[ P ]
= k2 [ ES ],
dt
d[ E ]
= −k1[ S ][ E ] + k−1[ ES ] + k2[ ES ],
dt
202
[E]0
0
Время, t
Концентрация
[E]0
[ES]
б
[P]
[E]
0
Время, t
Рисунок 112 – Изменение концентрации реагентов каталитической реакции от
времени: а – стационарное течение реакции; б – предстационарный интервал времени
203
Особенностью этого рисунка является то, что можно выделить два
характерных временных интервала:
1) "стационарный" интервал, в котором концентрация "промежуd[ ES ]
= 0 и скоточного" фермент-субстратного комплекса не меняется
dt
рость образования продукта является постоянной (угол наклона
зависимости [P] от времени приблизительно постоянен);
Величина
1
KM
характеризует прочность фермент-субстратного
комплекса – меньшее значение K M соответствует более прочному связыванию субстрата с ферментом.
9.8. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
2) "предстационарный" или "индукционный" интервал (рисунок 112(б)), предшествующий стационарному, в котором не выполняется
условие стационарности [ ES ] = const .
Задачи по ферментативной кинетике входят во вторую модульную
контрольную работу и в экзаменационные билеты по курсу "Ферментативный катализ". В качестве образца решения и оформления такого рода
заданий рекомендуется следующая задача.
Чем больше начальный избыток субстрата над ферментом
[ S ]0 [ E ]0 , тем короче индукционный участок.
ЗАДАЧА.
Для случая двух последовательных реакций первого порядка
d[ ES ]
= 0 , позволяет
dt
значительно упростить выражения кинетических уравнений.
Из выражения
Условие стационарности, т. е. [ ES ] = const и
d[ ES ]
= k1[ S ][ E ] − k−1[ ES ] − k2[ ES ] = 0
dt
непосредственно следует
k−1 + k2 [ E ][ S ]
=
.
k1
[ ES ]
Вид правой части уравнения соответствует выражению для константы равновесия для диссоциации комплекса [ ES ] на продукты [ E ] и
[S ] , которую в энзимологии называют константой Михаэлиса K M
KM =
[ E ][ S ] k−1 + k2
=
.
[ ES ]
k1
204
k1
k2
A → B → P показать, что выражение для зависимости концентрации
B
от времени имеет максимум
промежуточного вещества
[ B] max
⎛k
= [ A] 0 ⎜⎜ 2
⎝ k1
k2
⎞ k1 − k 2
⎟⎟
.
⎠
РЕШЕНИЕ.
Рассмотрим последовательную реакцию, состоящую из двух односторонних мономолекулярных элементарных стадий,
k1
k2
A→ B → P.
Система кинетических уравнений для этого случая имеет вид
d[ A]
= −k1[ A],
dt
d[ B ]
= k1[ A] − k2 [ B],
dt
d[ P ]
= k2[ B ].
dt
205
Для того чтобы решить первое дифференциальное уравнение системы,
разделяем переменные
d[ A]
k1 d t = −
[ A]
и интегрируем части в пределах (0, t ) и ([ A]0 ,[ A]) соответственно
t
[ A]
0
[ A ]0
∫ k1 d t = − ∫
d[ A]
,
[ A]
k1t = −(ln[ A] − ln[ A] 0 ) ,
k1t = ln
[ A]0
k1
( −k1 exp(−k1t ) + k2 exp(−k2t ) ) +
k2 − k1
+ k2 [ A]0
1
( −k1 exp(−k1t ) + k2 exp(−k2t ) + k2 exp(−k1t ) − k2 exp(−k2t ) ) = exp(−k1t ) ,
k2 − k1
1
(k 2 exp(−k1t ) − k1 exp(−k1t ) ) = exp(−k1t ) – тождество.
k 2 − k1
Подставим это выражение в третье уравнение системы
d[ P] k2 k1[ A]0
=
( exp(−k1t ) − exp(−k2t ) ) .
dt
k2 − k1
[ A] 0
.
[ A]
Откуда получаем решение первого кинетического уравнения системы
1 [ A] 0
k1 = ln
,
t
[ A]
[ A] = [ A] 0 exp(−k1t ),
Решение этого уравнения получим, используя соотношение материального баланса
[ A]0 − [ A] = [ B] + [ P] ,
откуда
где [ A]0 – концентрация вещества A в начальный момент времени t = 0 ;
[ P] = [ A]0 − [ A] − [ B] .
[ A] – концентрация в момент времени t .
Подставим выражение [ A] = [ A]0 exp(−k1t ) во второе уравнение системы и получим
Подставляем в [ P] = [ A]0 − [ A] − [ B ] выражения [ A] = [ A]0 exp(−k1t ) и
[ B] = [ A]0
d[ B ]
= k1[ A]0 exp(−k1t ) − k2 [ B] .
dt
Решение этого уравнения имеет вид
k [ A]
[ B] = 1 0 (exp(−k1t ) − exp(− k 2t ) ).
k 2 − k1
Действительно, подставим решение и сократим k1[ A]0
206
k1
( exp(−k1t ) − exp(−k2t ) ) = k1[ A]0 exp(−k1t ),
k2 − k1
k1
(exp(−k1t ) − exp(−k 2t ) ) . В результате получаем
k 2 − k1
[ P] = [ A]0 − [ A]0 exp(−k1t ) − [ A]0
k1
(exp(−k1t ) − exp(−k 2t ) ) ,
k 2 − k1
⎛
⎞
k1
k1
[ P] = [ A]0 ⎜⎜1 − exp(− k1t ) −
exp(−k1t ) +
exp(−k 2t ) ⎟⎟ ,
k
k
−
−
k
k
⎝
⎠
2
1
2
1
⎛
⎞
k2
k1
[ P] = [ A]0 ⎜⎜1 −
exp(−k1t ) +
exp(−k 2t ) ⎟⎟ .
k 2 − k1
⎝ k 2 − k1
⎠
207
На кинетической кривой для промежуточного вещества B имеется макd[ B]
симум. Его координаты получаем из условия
=0
dt
k1 [ A] 0
(exp(−k1t ) − exp(−k 2 t ) ) = 0
k 2 − k1
⎛
k1 [ A] 0 ⎜ ⎛ k 2
[ B] max (t max ) =
⎜⎜
k 2 − k1 ⎜ ⎜⎝ k1
⎝
⎛
k [ A] ⎜ ⎛ k
= 1 0 ⎜ ⎜⎜ 2
k 2 − k 1 ⎜ ⎝ k1
⎝
Следовательно
k [ A] ⎛ k
= 1 0 ⎜⎜ 2
k 2 − k1 ⎝ k1
exp(−k1t ) = exp(−k 2 t ) ,
откуда
(k 2 − k1 )t max = ln
⎛k
= [ A] 0 ⎜⎜ 2
⎝ k1
k2
k1
[ B] =
k1
ln (k 2 k1 )
=
.
k 2 − k1
Значение [ B] max (t max ) получим, подставив t max =
ln (k 2 k1 )
в выражение
k 2 − k1
ln ( k2 k1 ) ⎞
ln ( k2 k1 ) ⎞ ⎞
⎛
⎛
k1[ A]0 ⎛
⎜ exp ⎜ −k1
⎟ − exp ⎜ −k2
⎟⎟ =
k2 − k1 ⎝
k
k
k2 − k1 ⎠ ⎠
−
⎝
⎝
2
1 ⎠
k1 ⎤ ⎞
k2 ⎤ ⎞ ⎤
⎡
⎛ ⎡
⎛ ⎡
k1[ A]0 ⎢
⎜ ⎢⎛ k2 ⎞ k1 −k2 ⎥ ⎟
⎜ ⎢⎛ k2 ⎞ k1 −k2 ⎥ ⎟ ⎥
exp ⎜ ln ⎜ ⎟
.
=
− exp ⎜ ln ⎜ ⎟
⎢
⎥⎟
⎢
⎥ ⎟⎥
k2 − k1 ⎢
⎜ ⎢⎝ k1 ⎠
⎟
⎜ ⎢⎝ k1 ⎠
⎟⎥
⎢
⎥
⎥
⎦⎠
⎦ ⎠⎦
⎝ ⎣
⎝ ⎣
⎣
Далее,
⎛k
− ⎜⎜ 2
⎝ k1
k2
k2
⎞ k1 − k 2
⎟⎟
⎠
⎞
⎟
⎟=
⎟
⎠
⎞ k1 − k 2 ⎛ k 2
⎞ k [ A]
⎟⎟
⎜⎜ − 1⎟⎟ = 1 0
⎠
⎝ k1
⎠ k 2 − k1
⎛ k2
⎜⎜
⎝ k1
k2
⎞ k1 − k 2 ⎛ k 2 − k1 ⎞
⎟⎟
⎜⎜
⎟⎟ =
⎠
⎝ k1 ⎠
k2
⎞ k1 − k 2
⎟⎟
.
⎠
k2
⎛k
[ B] max (t max ) = [ A] 0 ⎜⎜ 2
⎝ k1
k2
⎞ k1 − k 2
⎟⎟
⎠
при t max =
ln(k 2 k1 )
.
k 2 − k1
ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОКОНТРОЛЯ
k1
1. Для простой равновесной кинетической схемы A→ B покажите, что
←
k−1
кинетическое уравнение для концентрации реагента A при условии:
в нулевой момент времени [ B]0 = 0 , имеет вид
[ A] = [ A]0 −
208
+1
порядка A → B → P выражение для зависимости концентрации промежуточного вещества B от времени имеет максимум
k1[ A]0
(exp(−k1t ) − exp(−k 2t ) ).
k 2 − k1
[ B]max (tmax ) =
k2
⎞ k1 − k 2
⎟⎟
⎠
k2
⎞
⎞ k1 − k 2 ⎟
⎟⎟
⎟=
⎠
⎟
⎠
ОТВЕТ.
Таким образом, для случая двух последовательных реакций первого
или
t max
k1
⎞ k1 − k 2 ⎛ k 2
⎟⎟
− ⎜⎜
⎠
⎝ k1
k1[ A]0
(1 − exp[−(k1 + k−1 )t ]) .
k1 + k−1
209
k1
Глава 10
k−1
СТАЦИОНАРНАЯ КИНЕТИКА МИХАЭЛИСА-МЕНТЕН
2. Для простой равновесной кинетической схемы A→ B покажите, что
←
кинетическое уравнение для концентрации реагента B при условии:
в нулевой момент времени [ B]0 = 0 , имеет вид
k [ A]
[ B] = 1 0 (1 − exp[−(k1 + k−1 )t ]) .
k1 + k−1
3. Для случая двух последовательных реакций первого порядка
k1
k2
A → B → P показать, что выражение для зависимости концентрации
реагента A от времени при начальном условии [ B]0 = [ P ]0 = 0 имеет
вид [ A] = [ A]0 exp(−k1t ) .
4. Для случая двух последовательных реакций первого порядка
k1
k2
A → B → P показать, что выражение для зависимости концентрации
промежуточного вещества B от времени при начальном условии
[ B]0 = [ P ]0 = 0 имеет вид
k [ A]
[ B] = 1 0 (exp(−k1t ) − exp(−k 2t ) ).
k 2 − k1
10.1. УРАВНЕНИЕ МИХАЭЛИСА
Перепишем константу Михаэлиса K M =
и воспользуемся уравнением материального баланса [ E ]0 = [ E ] + [ ES ] в
виде [ E ] = [ E ]0 − [ ES ] . Тогда [ ES ] = ([ E ]0 − ES ])
w=
d[ P]
k [E ] [S ]
= k2 [ ES ] = 2 0
dt
K M + [S ]
называется уравнением Михаэлиса
w=
k2[ E ]0 [ S ]
.
K M + [S ]
k2
A → B → P показать, что выражение для зависимости концентрации
продукта P от времени при начальном условии [ B]0 = [ P]0 = 0 име-
⎞
⎛
k2
k1
ет вид [ P] = [ A]0 ⎜⎜1 −
exp(−k1t ) +
exp(−k 2t ) ⎟⎟ .
k 2 − k1
⎠
⎝ k 2 − k1
6. Для случая двух последовательных реакций первого порядка
k1
[ E ]0 [ S ]
[S ]
или [ ES ] =
.
KM
K M + [S ]
Выражение для скорости появления продукта (скорости реакции)
5. Для случая двух последовательных реакций первого порядка
k1
[ E ][ S ]
[ E ][ S ]
в виде [ ES ] =
KM
[ ES ]
k2
A → B → P показать, что выражение для зависимости концентрации
промежуточного вещества B от времени имеет максимум при
ln(k 2 k1 )
t=
.
k 2 − k1
7. Запишите систему кинетических уравнений для некатализируемой
k1
k2
Зависимость скорости реакции от концентрации субстрата приведена на рисунке 113.
w
wmax
0,5wmax
[S]
KM
реакции A + B → X → P с одним промежуточным соединением.
←
Рисунок 113 – Зависимость скорости реакции от концентрации субстрата
210
211
k −1
Скорость не зависит от концентрации субстрата в присутствии избытка S и пропорциональна ей при низких концентрациях S .
Таким образом, простая кинетическая модель, описываемая уравнеk1
Преобразуем уравнение Михаэлиса в вид
1 K M + [S ]
=
,
w wmax [ S ]
k2
нием E + S → ES → E + P , может объяснить загадочное отсутствие кон←
k −1
центрационной зависимости, иногда наблюдаемое в ферментативных
реакциях.
При больших концентрациях субстрата скорость стремится к максимальному значению
wmax = k 2 [E ]0 ,
поэтому, уравнение Михаэлиса можно записать в виде
а затем в уравнение Лайнуивера-Берка (Lineweaver-Burk)
1 KM 1
1
=
+
.
w wmax [ S ] wmax
График уравнения Лайнуивера-Берка, представляющий собой пря⎛1 1 ⎞
мую в координатах ⎜ ,
⎟ , приведен на рисунке 114.
⎝ w [S ] ⎠
тангенс угла
наклона =
1
w
w [S ]
w = max
.
K M + [S ]
wmax
константа Ми2
= [ S ] – константа Михаэлиса равна концентрации субстра-
=
KM
wmax
Из уравнения Михаэлиса следует, что при w =
хаэлиса K M
та, при которой скорость (стационарной) реакции достигает половины
своего максимального значения.
1
wmax
1
[S ]
1
−
KM
10.2. ПРИБЛИЖЕНИЕ ЛАЙНУИВЕРА-БЕРКА
Уравнение Михаэлиса w =
wmax [ S ]
описывает гиперболу, и нахоK M + [S ]
ждение значений wmax и K M из зависимости w([S ]) требует набора данных во всем диапазоне концентраций.
Стандартным решением такой проблемы является приведение исследуемой зависимости к уравнению прямой путем преобразования координат. В энзимологии одним из наиболее популярных является подход,
предложенный Лайнуивером и Берком.
Рисунок 114 – График Лайнуивера-Берка
По графику уравнения Лайнуивера-Берка удобно определять wmax ,
K M и k 2 . Для этого продолжают прямую до пересечения её с осью абсцисс и ординат.
1. Значение максимальной скорости wmax равно обратной величине
отрезка, отсекаемого прямой Лайнуивера-Берка на оси ординат.
2. Значение константы Михаэлиса K M равно обратной величине
отрезка, отсекаемого прямой Лайнуивера-Берка на оси абсцисс.
212
213
10.3. СМЫСЛ ПАРАМЕТРОВ КИНЕТИКИ МИХАЭЛИСА-МЕНТЕН
Максимальная скорость ферментативной реакции wmax . По-
скольку wmax = k 2 [ E ]0 , то wmax можно использовать в качестве характеристики количества фермента, присутствующего в неизвестном растворе (для "оценки" активности фермента). Обычно wmax выражают в единицах ферментативной активности, например в международных единицах
МЕ (1 микромоль/с) при условии, что фермент насыщен субстратом.
На практике измерение активности в крови фермента аспартатаминотрансферазы позволяет в три раза увеличить достоверность диагностирования инфаркта миокарда, при котором резко повышается
активность этого фермента в сыворотке крови.
Константа Михаэлиса K M . Параметр K M в первую очередь ис-
пользуют для выявления специфичности действия фермента, поскольку
K M характеризует тенденцию фермент-субстратного комплекса к диссо-
Рисунок 115 – Схема, иллюстрирующая специфичность действия разных протеолитических ферментов
На рисунке 116 представлена схема фермента лизоцима, аминокислотная последовательность которого была определена с помощью предварительного протеолиза протеолитическими ферментами.
циации на фермент и субстрат.
Сравнивая значения K M для ряда различных субстратов, можно
определить, какой тип молекул наиболее прочно связывается с ферментом; как правило, к числу наиболее прочно связывающихся субстратов
(т.е. K M малы) относятся "природные" субстраты (субстраты, на которые
фермент действует in vivo).
Проводя такие исследования, можно, например, классифицировать
различные протеолитические ферменты (ферменты, которые гидролизируют белки) согласно тому, на какие участки полипептидной цепи они
действуют. На рисунке 115 представлена схема действия некоторых протеолитических ферментов. Например, химотрипсин расщепляет цепь, атакуя карбоксильный конец связи между тирозином и соседним
аминокислотным остатком. Проявление подобной специфичности часто
используется для расщепления белка по заданным участкам перед аминокислотным анализом. Проводя расщепление в нескольких различных (известных) участках и анализируя получающиеся при этом продукты,
можно установить аминокислотную последовательность в белке.
214
Рисунок 116 – Последовательность аминокислотных остатков в ферменте лизоцим (см. рисунок 73)
215
Константа скорости k 2 второго этапа реакции. Если концентрация
фермента известна (например при работе с очищенными ферментными
w
препаратами), то из wmax можно определить k2 = max .
[ E ]0
Параметр k 2 характеризует эффективность ферментативного катализа и используется для получения информации о его механизмах.
k 2 – каталитическая константа, часто обозначается как kcat или
kc – может рассматриваться как число молей продукта, образующихся в
единицу времени одним молем чистого фермента, насыщенного субстратом.
Числом превращения называется отношение k 2 к числу активных
центров в молекуле фермента. Таким образом, число превращения показывает количество молей продукта, образуемых в единицу времени (в 1 с)
на одном активном центре фермента, насыщенном субстратом.
Как показано в таблице 8, типичные значения чисел превращения
лежат в интервале 1–1 000 000.
Каталазная ферментативная система задействована в защитном механизме жука-бомбардира. На кончике брюшка этого жука находится
"реакторная железа", содержащая 25% H 2 O 2 . Если потревожить жука, то
каталазная реакция протекает так быстро, что за 1 с вода в "реакторной
железе" нагревается от комнатной температуры до 100°С и под действием
образующегося пара в нападающего выстреливается струя кипящей воды.
10.4. СНЯТИЕ ОГРАНИЧЕНИЙ МИХАЭЛИСА-МЕНТЕН ДЛЯ СЛУЧАЯ
ОБРАТНОЙ РЕАКЦИИ
Если обратная реакция между ферментом и продуктом возможна, то
схема реакции будет иметь вид
Число превращения
Химотрипсин
Рибонуклеаза
Карбоксипептидаза
Киназа
Каталаза
Пероксидаза
Карбоангидраза
1 000
100
100
1 000
5 000 000
10
36 000 000
Фермент каталаза, катализирующий реакцию 2H 2O 2 → 2H 2O + O 2 ,
обеспечивает одну из наиболее высоких скоростей превращения, известных для хорошо изученных ферментов.
216
k2
k−1
k−2
Скорость изменения концентрации фермент-субстратного комплекса
d[ ES ]
= k1[ E ][ S ] − (k−1 + k2 )[ ES ] + k−2[ E ][ P] .
dt
Таблица 8 – Числа превращения для некоторых ферментов
Фермент
k1
E + S → ES → E + P .
← ←
При стационарных условиях
d[ ES ]
= 0,
dt
следовательно
k1[ E ][ S ] − (k−1 + k2 )[ ES ] + k−2[ E ][ P] = 0 ,
[ ES ] =
k1[ S ] + k−2 [ P]
[E] .
k−1 + k2
Подставим в это уравнение выражение [ E ] = [ E ]0 − [ ES ] из уравнения материального баланса [ E ]0 = [ E ] + [ ES ] и получим
217
[ ES ] =
[ ES ] +
k1[ S ] + k−2 [ P]
([ E ]0 − [ ES ]) ,
k −1 + k 2
k1[ S ] + k−2[ P ]
k [ S ] + k −2 [ P ]
[ ES ] = 1
[ E ]0 ,
k−1 + k2
k−1 + k2
⎛ k [ S ] + k−2[ P ] ⎞ k1[ S ] + k−2 [ P]
[ ES ] ⎜1 + 1
[ E ]0 ,
⎟=
k−1 + k2 ⎠
k−1 + k2
⎝
⎛ k + k + k [ S ] + k−2[ P ] ⎞ k1[ S ] + k−2[ P ]
[ ES ] ⎜ −1 2 1
[ E ]0 ,
⎟=
k−1 + k2
k−1 + k2
⎝
⎠
k1[ S ] + k−2[ P]
[ ES ] =
[ E ]0 .
k−1 + k2 + k1[ S ] + k−2 [ P]
Скорость изменения концентрации продукта
d[ P]
= k2 [ ES ] − k−2 [ E ][ P ] = k2 [ ES ] − k−2 ([ E ]0 − [ ES ])[ P ] =
dt
= [ ES ](k2 + k−2[ P]) − k−2 [ E ]0 [ P] =
w=
=
(k1[ S ] + k−2 [ P])[ E ]0 (k2 + k−2[ P])
− k−2[ E ]0 [ P] =
k−1 + k2 + k1[ S ] + k−2[ P ]
⎛ (k [ S ] + k−2[ P])(k2 + k−2 [ P ])
⎞
= [ E ]0 ⎜ 1
− k−2[ P ] ⎟ =
⎠
⎝ k−1 + k2 + k1[ S ] + k−2 [ P ]
(k1k2 [ S ] − k−1k−2[ P ])[ E ]0
=
.
k−1 + k2 + k1[ S ] + k−2[ P ]
В начальный момент времени, когда продукт в системе отсутствует
( [ P] = 0 )
wпрямая =
k1k2 [ S ][ E ]0
k [ S ][ E ]0
wS [ S ]
,
= 2
= Smax
k−1 + k2 + k1[ S ] k−1 + k2 + [ S ] K M + [ S ]
k1
таким образом, уравнение принимает вид уравнения Михаэлиса.
Если концентрация субстрата падает до нуля [ S ] = 0 , то
218
wобратная =
(−k−1k−2 [ P])[ E ]0 −k−1[ P][ E ]0
wP [ P]
=
= Pmax
k−1 + k2 + k−2 [ P] k−1 + k2 + [ P] K M + [ P ]
k −2
и уравнение также принимает вид уравнения Михаэлиса по отношению к
продукту для обратной реакции.
Эти предельные случаи очень важны.
Во-первых, если ферментативная реакция действительно обратима,
то обратная реакция также является каталитической, и если в начале реакции в системе находится фермент и продукт, для обратной реакции
wmax и K MP определяются так же просто, как если бы измерялась скорость
прямой каталитической реакции.
Во-вторых, осложнения, обусловливаемые наличием обратной реакции, как правило, можно обойти, просто ограничивая измерения экспериментами, в которых [ P ] ≈ 0 .
Скорость образования продукта w обратимой ферментативной реакции уменьшается по двум причинам.
Во-первых, некоторое количество продукта в результате обратной
реакции превращается обратно в субстрат – вычитаемое k −1k −2 [ P] в
числителе выражения
w=
(k1k2 [ S ] − k−1k−2[ P ])[ E ]0
.
k−1 + k2 + k1[ S ] + k−2[ P ]
Во-вторых, увеличивается доля фермента, связанного в комплексе
EP с продуктом, который не может взаимодействовать с субстратом –
слагаемое k −2 [ P] в знаменателе.
Таким образом, обратимая ферментативная реакция
k1
k2
k−1
k−2
E + S → ES → E + P ,
← ←
219
описываемая уравнением w =
(k1k2 [ S ] − k−1k−2[ P ])[ E ]0
, служит примером
k−1 + k2 + k1[ S ] + k−2[ P ]
Далее
(k−1 + k3 )[ ES ] + k1[ ES ][ S ] = k1[ E ]0[ S ] − k1[ EP ][ S ] + k−3[ EP] ,
простой биологической регуляции на молекулярном уровне:
[ ES ] =
• продукт образуется быстро, только если его мало,
• продукт образуется медленнее, если концентрация [P] велика.
10.5. СНЯТИЕ ОГРАНИЧЕНИЙ МИХАЭЛИСА-МЕНТЕН ДЛЯ РЕАКЦИЙ
Подставляем это выражение во второе кинетическое уравнение системы
С ЧИСЛОМ ПРОМЕЖУТОЧНЫХ СОЕДИНЕНИЙ БОЛЬШЕ ОДНОГО
d[ EP ]
= k3[ ES ] − (k−3 + k2 )[ EP] = 0 ,
dt
k [ E ] [ S ] − k1[ EP ][ S ] + k −3 [ EP]
k3 1 0
− (k −3 + k 2 )[ EP] = 0
k −1 + k 3 + k1[ S ]
Будем считать теперь, что природа фермент субстратного комплекса изменяется в ходе протекания реакции
k1
k3
k−1
k−3
k1[ E ]0[ S ] − k1[ EP][ S ] + k−3[ EP]
.
k−1 + k3 + k1[ S ]
k2
E + S → ES → EP → E + P .
← ←
При стационарных условиях [ ES ] = const , [ EP] = const система кинетических уравнений будет иметь вид
d[ ES ]
= k1[ E ][ S ] + k−3[ EP] − (k−1 + k3 )[ ES ] = 0,
dt
d[ EP ]
= k3[ ES ] − (k−3 + k2 )[ EP ] = 0,
dt
d[ P ]
= k2 [ EP ].
w=
dt
и решаем его относительно [EP] . Выражение
k3 (k1[ E ]0 [ S ] − k1[ EP][ S ] + k−3[ EP ]) − (k−1 + k3 + k1[ S ])(k−3 + k2 )[ EP ]
=0
k−1 + k3 + k1[ S ]
выполняется, если числитель равен нулю.
k3k1[ E ]0[ S ] − k3k1[ EP ][ S ] + k3k−3[ EP] −
− (k−1k−3 + k−1k2 + k3k−3 + k3k2 + k1k−3[ S ] + k1k2 [ S ])[ EP ] = 0
или
k3k1[ E ]0 [ S ] − k3k1[ EP][ S ] + k3k−3[ EP] − k−1k−3[ EP] − k−1k2[ EP] −
Уравнение материального баланса
− k3k−3[ EP ] − k3k2[ EP] − k1k−3[ S ][ EP ] − k1k2 [ S ][ EP] = 0,
[ E ]0 = [ E ] + [ ES ] + [ EP] или [ E ] = [ E ]0 − [ ES ] − [ EP] .
Подставляем в первое кинетическое уравнение системы выражение
[ E ] = [ E ]0 − [ ES ] − [ EP]
0 = k1[ E ][ S ] + k−3[ EP] − (k−1 + k3 )[ ES ] =
= k1 ([ E ]0 − [ ES ] − [ EP ])[ S ] + k−3[ EP ] − (k−1 + k3 )[ ES ].
220
откуда
k3k1[ E ]0 [ S ] = [ EP ](+ k3k1[ S ] − k3k−3 + k−1k−3 + k−1k2 +
+ k3k−3 + k3k2 + k1k−3[ S ] + k1k2[ S ])
или
221
[ EP] =
Хотя смысл кажущихся K S и wmax в терминах констант скоростей
k3k1[ E ]0 [ S ]
.
k−1k−3 + k−1k2 + k3k2 + [ S ]k1 (k3 + k−3 + k2 )
элементарных реакций совершенно другой, экспериментальная зависи⎛1 1 ⎞
мость в координатах Лайнуивера-Берка ⎜ ,
⎟ по-прежнему описыва⎝ w [S ] ⎠
KS
, пересекающей ось ординат при
ется прямой с углом наклона
wmax
Подставляем это выражение в скорость образования продукта
w=
d[ P]
= k2 [ EP]
dt
значении y =
и получаем
w=
Таким образом, описанный вывод указывает на одну из самых серьезных слабостей стационарной кинетики ферментативных реакций, а
именно, на невозможность по данным стационарной кинетики детектировать наличие нескольких промежуточных соединений в реакции.
Это пример типичной проблемы, которая возникает при постановке
научных экспериментов, когда усложненная и детализированная теория
бесполезна, если экспериментальные данные не позволяют её проверить.
k3k2 k1[ E ]0[ S ]
.
k−1k−3 + k−1k2 + k3k2 + [ S ]k1 (k3 + k−3 + k2 )
Это выражение внешне подобно уравнению Михаэлиса
w=
wmax [ S ]
.
K M + [S ]
Действительно, если разделить
k1 (k 3 + k −3 + k 2 ) , то получим
числитель
и
знаменатель
на
k3k2 k1[ E ]0
[S ]
k1 (k3 + k−3 + k2 )
w [S ]
,
w=
= max
k−1k−3 + k−1k2 + k3k2
K
S + [S ]
+ [S ]
k1 (k3 + k−3 + k2 )
здесь wmax =
k3k2 k1[ E ]0
, а роль константы Михаэлиса выполняет выk1 (k3 + k−3 + k2 )
ражение K S =
k−1k−3 + k−1k2 + k3k2
.
k1 (k3 + k−3 + k2 )
Таким образом, введение второго промежуточного соединения в
основную кинетическую схему Михаэлиса-Ментен приводит к результату, который в кинетике стационарных реакций невозможно экспериментально отличить от упрощенного случая с одним промежуточным
соединением.
222
1
.
wmax
10.6. МУЛЬТИСУБСТРАТНЫЕ РЕАКЦИИ
Большинство ферментативных реакций в биологических системах
являются мультисубстратными. Рассмотрим особенности мультисубстратных реакций на примере бисубстратной реакции типа A + B → C + D .
Схематически такого типа реакции представлены на рисунке 117.
Большинство таких реакций заключается в переносе функциональных групп, таких как фосфорильная или аминогруппа, от одного субстрата к другому. В окислительно-восстановительных реакциях между
субстратами переносятся электроны.
Мультисубстратные реакции условно разделяют на два класса:
1) реакции с образованием тройного комплекса (реакции последовательного замещения (sequential displacement));
2) "пинг-понг"-реакции (реакции двойного замещения (double
displacement)).
223
ции. Лактатдегидрогеназа восстанавливает пируват в лактат, окисляя
при этом NADH в NAD+
В упорядоченных реакциях последовательного замещения кофермент NADH всегда присоединяется первым, а лактат всегда десорбирует первым. Эта последовательность схематически изображена на
рисунке 118 в виде, предложенном Клеландом.
NADH
Рисунок 117 – Схема бисубстратной ферментативной реакции: 1 – свободный
фермент Е; 2 – комплекс Е·А; 3 – Комплекс Е·А·В; 4 – Переходное состояние Е≠;
5 – Комплекс Е·С·D; 6 – комплекс E·D
В реакциях с образованием тройного комплекса все субстраты
должны быть сорбированы на ферменте, прежде чем, какой либо продукт
реакции будет десорбирован. Так, в бисубстратной реакции образуется
тройной комплекс: фермент и оба субстрата.
Реакции с образованием тройного комплекса бывают двух типов:
1) упорядоченные, в которых субстраты сорбируются на ферменте в
строго определенном порядке,
2) неупорядоченные (статистические), в которых порядок присоединения субстратов к ферменту произволен.
Фермент
Пируват
Лактат
Фермент-NADH-Пируват ⇔ Фермент-Лактат-NAD+
Фермент
Рисунок 118 – Схема Клеланда упорядоченной каталитической бисубстратной
реакции восстановления пирувата в лактат на лактатдегидрогеназе
Фермент-субстратный комплекс представляет собой тройной комплекс: сначала он состоит из фермента и субстратов, а затем из фермента
и продуктов.
В статистических (неупорядоченных) реакциях порядок, в котором
субстраты присоединяются к ферменту произволен. Например, креатинкиназа (ЕС 2.7.3.2) образует фосфокреатин и АДФ из креатина и АТФ
Например, многие ферменты, использующие NAD+ или NADH в
качестве субстратов, демонстрируют упорядоченный механизм. Рассмотренный в п. 8.1 пример каталитического цикла лактатдегидрогеназы
(ЕС 1.1.1.27) представляет собой характерный пример такого рода реак224
NAD+
225
Второй субстрат, α-кетоглютарат, сорбируется на модифицированном ферменте, присоединяет аминогруппу и продукт, глутаминовая кислота (глутамат), десорбирует с фермента.
Схема Клеланда этой реакции изображена на рисунке 119.
АТФ
Креатин
Фосфокреатин АДФ
Фермент
Фермент
Е-АТФ- ⇔ Е-АДФ-Креатин
-Фосфокреатин
Креатин АТФ
АДФ Фосфокреатин
Рисунок 119 – Схема Клеланда статистической каталитической бисубстратной
реакции образования фосфокреатина
В "пинг-понг" реакциях один или более продуктов реакции десорбирует ещё до того момента, когда все субстраты присоединятся к ферменту. Определяющей особенностью этого механизма является
существование промежуточного состояния фермента, в котором молекула фермента временно модифицирована.
Классическим примером такого механизма является реакция, в ко-
торой аминогруппа переносится между аминокислотой и α-кетокислотой.
Фермент аспартатаминотрансфераза (ЕС 2.6.1.1) катализирует перенос
аминогруппы от аспарагиновой кислоты (аспартата) к α-кетоглютарату.
аспартат
α-кетоглютарат
оксалоацетат
глутамат
Фермент
Фермент
Е
⇔ (Е-NH3) ⇔ (Е-NH3) ⇔ (Е-NH3) ⇔
E
(аспартат) (оксалоацетат)
(α-кетоглютарат) (глутамат)
Рисунок 120 – Схема Клеланда каталитической бисубстратной реакции типа
"пинг-понг"
Фермент работает как своего рода почтовый ящик, в котором первый субстрат (почтальон) оставил функциональную группу (почту), а второй субстрат (клиент) её забрал. Пустой почтовый ящик – это фермент, а
ящик с почтой – временная модифицированная форма этого фермента.
Субстраты сорбируют и десорбируют на ферменте как мячики настольного тенниса ударяются об игровой стол, поэтому такой механизм
получил название "пинг-понг"-механизм.
10.7. СНЯТИЕ ОГРАНИЧЕНИЙ МИХАЭЛИСА-МЕНТЕН ДЛЯ МУЛЬТИСУБСТРАТНЫХ РЕАКЦИИ
Приближение Лайнуивера-Берка позволяет различить упорядоченные, статистические и "пинг-понг" мультисубстратные реакции.
Схемы этих механизмов (для случая двух субстратов A и B и двух
продуктов P и Q ) имеют вид:
– статистический механизм
Схема Клеланда этой реакции представлена на рисунке 120. После
сорбции аспартата фермент присоединяет к себе аминогруппу, образуя
временную модифицированную форму. После этого первый продукт, оксалоацетат, десорбирует.
226
E + A ↔ EA
EP ↔ E + P
7
7
EAB ↔ EPQ
7
7
E + B ↔ EB
EQ ↔ E + Q,
227
– упорядоченный механизм
w=
E + A ↔ EA ↔ EAB ↔ EPQ ↔ EQ ↔ E + Q ,
– "пинг-понг" реакция
Уравнение вида w =
E + A ↔ EA ↔ EP ↔ E ′ + P,
E ′ + B ↔ EB ↔ EQ ↔ E + Q.
В реакции, происходящей по статистическому и упорядоченному
механизмам, образуется тройной комплекс – оба субстрата должны связаться с ферментом до того, как реакция произойдет.
В реакции типа "пинг-понг" фермент сначала связывается и осуществляет превращение первого субстрата, а затем происходит взаимодействие со вторым субстратом.
Оказалось, что кинетика реакций с образованием тройных комплексов описывается уравнением
w=
V [ A][ B]
,
C0 + C1[ A] + C 2 [ B ] + [ A][ B]
а кинетика "пинг-понг" реакций – уравнением
w=
V [ A][ B ]
V [ A]
V [ A]
=
≈
.
[
]
C
A
C1[ A] + C2 [ B ] + [ A][ B ]
1
+ C2 + [ A] C2 + [ A]
[ B]
V [ A][ B ]
,
C1[ A] + C 2 [ B] + [ A][ B]
хаэлиса, полученным при рассмотрении схемы Михаэлиса-Ментен для
реакции с одним субстратом.
Эта ситуация типична для любой ферментативной реакции (например, гидролиз эфиров), при которой одним из реагентов является вода,
например для многих ферментативных процессов в желудочно-кишечном
тракте (с ферментами трипсин, химотрипсин, пепсин и т.д.).
Кроме того, важной особенностью этих уравнений скоростей двухсубстратных реакций является то, что при постоянной концентрации второго субстрата (пусть, например, [ B] = const ) и изменении концентрации
первого субстрата A зависимость
w=
V [ A][ B]
V [ A]
V [ A]
=
≈
,
C0 + C1[ A] + C2[ B] + [ A][ B] C0 + C1[ A] + C + [ A] C2 + [ A]
2
[ B] [ B]
228
1
1
(зависимость Лайнуивераот
w
[ A]
Берка) описывается уравнением прямой.
Действительно, при [ B] = const уравнения
w=
V [ A][ B]
,
C0 + C1[ A] + C2 [ B] + [ A][ B]
w=
где C0 , C1 и C2 – комбинации разных констант скоростей в соответствующих механизмах.
Характерные особенности этих уравнений.
Первое, если один из субстратов присутствует в избытке, например
[ B]0 [ A]0 , то оба уравнения упрощаются до одинакового вида:
V [ A]
внешне совпадает с уравнением МиC 2 + [ A]
V [ A][ B]
C1[ A] + C2 [ B] + [ A][ B]
можно переписать в виде
1 C0 + C1[ A] + C2 [ B] + [ A][ B] ⎛ C0
C ⎞ 1 ⎛ C1
1⎞
=
=⎜
+ 2⎟
+⎜
+ ⎟,
w
V [ A][ B ]
⎝ V [ B ] V ⎠ [ A] ⎝ V [ B] V ⎠
1 C1[ A] + C2[ B ] + [ A][ B ] C2 1 ⎛ C1
1⎞
=
=
+
+
.
w
V [ A][ B ]
V [ A] ⎜⎝ V [ B] V ⎟⎠
229
Характер изменения зависимостей
1
1
, при проведении измеот
w
[ A]
1
w
рений с различными значениями постоянной концентрации [ B1 ] = const ,
[ B ] = const − растёт
[ B2 ] = const , [ B3 ] = const , [ B4 ] = const , [ B1 ] < [ B2 ] < [ B3 ] < [ B4 ] , будет различен в случаях реакций с образованием тройных комплексов и в "пингпонг" реакциях.
Действительно, в реакциях с образованием тройного комплекса поC ⎞
⎛ C
стоянная концентрация реагента B входит и в коэффициент ⎜ 0 + 2 ⎟
[
]
V
B
V ⎠
⎝
1
при
(тангенс угла наклона прямой) и в постоянный коэффициент
[ A]
⎛ C1
1⎞
+ ⎟.
⎜
⎝ V [ B] V ⎠
Поэтому увеличение концентрации B в ряду [ B1 ] < [ B2 ] < [ B3 ] < [ B4 ]
будет приводить одновременно и к смещению прямых вниз по оси
−
1
[ A]
1 C1C
−
V VC0
Рисунок 121 – Зависимости Лайнуивера-Берка для мультисубстратных реакций
с образованием тройного комплекса
Откуда получаем
⎛ C0
C0 ⎞
C1
C1
⎟⎟ ⋅ x =
⎜⎜
−
−
,
V
[
B
]
V
[
B
]
V
[
B
]
V
[ B1 ]
⎝
1
2 ⎠
2
1
,ик
w
уменьшению угла наклона (рисунок 121).
При этом прямые пересекаются в одной точке, координаты которой
можно легко получить, решив систему уравнений относительно коорди1
1
,
нат y = и x =
w
[ A]
C1
C0
C0 [ B2 ] − [ B1 ]
C [ B ] − [ B1 ]
x=− 1 2
.
V [ B1 ][ B2 ]
V [ B1 ][ B2 ]
Следовательно
x=−
⎛ C
⎛ C
C ⎞
1⎞
y1 = ⎜ 0 + 2 ⎟ ⋅ x + ⎜ 1 + ⎟ ,
⎝ V [ B1 ] V ⎠
⎝ V [ B1 ] V ⎠
⎛ C
⎛ C
C ⎞
1⎞
y2 = ⎜ 0 + 2 ⎟ ⋅ x + ⎜ 1 + ⎟ .
⎝ V [ B2 ] V ⎠
⎝ V [ B2 ] V ⎠
В точке пересечения y1 = y2
C1
,
C0
при котором
⎛ C
C
y = ⎜⎜ 0 + 2
⎝ V [ B1 ] V
⎞ ⎛ C1
⎟⎟ ⋅ ⎜⎜ −
⎠ ⎝ C0
⎞
C1
1 1 CC
⎟⎟ +
+ = − 1 2.
⎠ V [ B1 ] V V VC 0
Таким образом, координаты точки пересечения прямых
⎛ C0
⎛ C
⎛ C
C ⎞
1⎞ ⎛ C
C ⎞
1⎞
+ 2 ⎟⋅ x + ⎜ 1 + ⎟ = ⎜ 0 + 2 ⎟⋅ x +⎜ 1 + ⎟.
⎜
⎝ V [ B1 ] V ⎠
⎝ V [ B1 ] V ⎠ ⎝ V [ B2 ] V ⎠
⎝ V [ B2 ] V ⎠
230
1 1 C1C2
= −
w V VC0
C
1
=− 1 ,
[ A]
C0
231
не зависят от величин [ B1 ] и [ B2 ] . Семейство прямых всегда пересекается
в точке слева от оси ординат. А её положение относительно оси абсцисс
определяется соотношением между величинами C0 , C1 , C2 ,V и знаком
выражения
1 C1C 2
−
.
V VC0
В "пинг-понг" реакциях величина [B] входит только в постоянный
⎛ C
1⎞
коэффициент ⎜ 1 + ⎟ . Поэтому увеличение концентрации B в ряду
V
[
B
]
V
⎠
⎝
[ B1 ] < [ B2 ] < [ B3 ] < [ B4 ] будет приводить только к смещению прямых вниз
по оси
1
(рисунок 122). Мы получаем семейство параллельных прямых.
w
1
w
[ B ] = const − растёт
1
[ A]
Рисунок 122 – Зависимости Лайнуивера-Берка для мультисубстратных реакций
типа "пинг-понг"
Таким образом, использование представления Лайнуивера-Берка
позволяет различить механизмы мультисубстратных реакций с образованием тройного комплекса и "пинг-понг" реакций.
Для установления различий между статистическим и упорядоченными механизмами требуются дальнейшие исследования (например, ингибирования или изотопного обмена).
Таким образом, основную кинетическую схему Михаэлиса-Ментен
k1
k2
E + S → ES → E + P можно обобщить, (1) допуская возможность обратной
←
k−1
реакции фермента с продуктом, (2) присутствие многих промежуточных
232
соединений и (3) присутствие двух субстратов, способных реагировать
раздельно ("пинг-понг") или одновременно (образование тройного комплекса) с ферментом.
Алгебраические сложности можно легко обойти, используя зависи1
1
(которая соответствует прямой).
от
мость Лайнуивера-Берка
w
[ A]
При этом:
1) ингибирующее влияние продукта сводится к минимуму ограничением измерений начальных скоростей реакций (так, чтобы эффективная концентрация продукта [P] была равна нулю),
2) поскольку вид уравнения скорости одинаков для ситуации и с одним, и с большим числом промежуточных соединений, введение в
схему дополнительных промежуточных фермент-субстратных
комплексов или комплексов фермента с продуктом бессмысленно,
3) влияние второго субстрата подавляется проведением эксперимента при условиях, при которых концентрация одного из двух
субстратов постоянна или избыточна.
Простая схема Михаэлиса-Ментен определяет простейший механизм, которым можно объяснить зависимость скоростей ферментативных
реакций от концентрации субстрата и фермента.
Однако попытка обобщить эту схему и применить её к более реальным (и, следовательно, более сложным) ситуациям дает сравнительно
мало новой информации.
ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОКОНТРОЛЯ
k1
k2
k −1
k−2
1. Для случая каталитической реакции E + S → ES → E + P , в которой
← ←
учтена обратная реакция между ферментом и продуктом, показать,
что при стационарных условиях выражение для скорости изменения
(k k [ S ] − k −1k −2 [ P ])[ E ]0
концентрации продукта имеет вид w = 1 2
.
k −1 + k 2 + k1[ S ] + k −2 [ P ]
233
k1
k2
k−1
k−2
2. Для случая каталитической реакции E + S → ES → E + P , в которой
← ←
учтена обратная реакция между ферментом и продуктом, показать,
что при стационарных условиях в начальный момент времени, когда
продукт реакции практически отсутствует в системе, выражение для
скорости изменения концентрации продукта имеет вид
k k [ S ][ E ]0
.
w= 1 2
k −1 + k 2 + k1[ S ]
k1
k2
3. Из сравнения с моделью Михаэлиса-Ментен ( E + S → ES → E + P ) по←
k−1
казать,
каким
k1
k2
k−1
k−2
образом
в
случае
каталитической
реакции
E + S → ES → E + P (в которой учтена обратная реакция между фер← ←
ментом и продуктом) частичное превращение продукта реакции обратно в субстрат уменьшает скорость образования продукта
d[ P]
w=
.
dt
4. Запишите систему кинетических уравнений для реакции
k1
k3
k−1
k−3
k2
E + S → ES → EP → E + P , в которой изменяется природа фермент← ←
субстратного комплекса.
k1
k3
k−1
k−3
k2
продукта которых имеет вид w =
зать, что в приближении Лайнуивера-Берка (зависимость
6. Для случая мультисубстратных каталитических реакций с образованием тройных комплексов, выражение для скорости образования
234
1
1
от
w
[ A]
при постоянном значении [B] ) увеличение концентрации B в ряду
[ B1 ] < [ B2 ] < [ B3 ] < [ B4 ] будет приводить одновременно и к смещению
прямых вниз по оси
1
и к уменьшению угла наклона.
w
7. Для случая мультисубстратных каталитических реакций с образованием тройных комплексов, выражение для скорости образования
V [ A][ B]
продукта которых имеет вид w =
, покаC0 + C1[ A] + C 2 [ B ] + [ A][ B]
зать, что для набора различных постоянных концентраций
[ B] = const , прямые Лайнуивера-Берка пересекаются при значении
C
1
=− 1 .
[ A]
C0
8. Для случая мультисубстратных каталитических реакций с образованием тройных комплексов, выражение для скорости образования
V [ A][ B]
продукта которых имеет вид w =
, покаC0 + C1[ A] + C 2 [ B ] + [ A][ B]
зать, что для набора различных постоянных концентраций
[ B] = const , прямые Лайнуивера-Берка пересекаются при значении
5. Для случая каталитической реакции E + S → ES → EP → E + P , в кото← ←
рой природа фермент-субстратного комплекса изменяется в ходе
протекания реакции, показать, что при стационарных условиях выражение для скорости изменения концентрации продукта имеет вид
k 3 k 2 k1[ E ]0 [ S ]
.
w=
k −1k −3 + k −1k 2 + k 3 k 2 + [ S ]k1 (k3 + k −3 + k 2 )
V [ A][ B ]
, покаC0 + C1[ A] + C 2 [ B ] + [ A][ B]
1 1 C1C2
= −
.
w V VC0
9. Для случая мультисубстратных каталитических реакций типа "пингпонг", выражение для скорости образования продукта которых имеет
V [ A][ B]
вид w =
, показать, что для набора различных
C1[ A] + C 2 [ B ] + [ A][ B]
постоянных концентраций [ B] = const , прямые Лайнуивера-Берка параллельны друг другу.
235
Глава 11
РЕГУЛЯЦИЯ СКОРОСТЕЙ ФЕРМЕНТАТИВНЫХ
РЕАКЦИЙ
11.1. РЕГУЛЯЦИЯ ФЕРМЕНТАТИВНОЙ АКТИВНОСТИ
В присутствии обратной реакции схема Михаэлиса-Ментен регулирует количество продукта, поскольку скорость его образования падает с
ростом его концентрации. Такая "естественная" "само"-регуляция происходит во всех ферментативных реакциях, в которых катализируется превращение субстрата в продукт.
Однако, как известно, существуют другие типы регуляции ферментативной активности, основанные на присутствии в системе химических
соединений, эффекторов, самих по себе не являющихся субстратами или
продуктами, однако способных связываться с молекулой фермента на
участках, которые, вообще говоря, могут быть удалены от каталитического активного центра фермента.
Действие таких внешних регуляторов (эффекторов) обеспечивает
эффективный контроль за скоростями ферментативных реакций и служит средством биохимического отклика системы на изменение внешних
условий путем изменения скоростей соответствующих ферментативных
реакций.
Внешние регуляторы ферментативных реакций можно разделить на
две группы.
В первую группу входят внешние регуляторы, которые неспецифичны в структурном отношении – их активность коррелирует с некоторыми феноменологическими физико-химическими свойствами, такими,
как, например:
• поверхностное натяжение в их растворах,
• растворимость,
• степень ионизации
236
в большей степени, чем с присутствием в их структуре каких-либо специфических функциональных химических группировок.
Примеры таких веществ – лекарственные вещества-анестетики общего действия, такие, как хлороформ или диэтиловый эфир, физиологическая активность которых коррелирует с размером их молекул и с
растворимостью в органических неполярных растворителях.
К другому подвиду первой группы веществ относятся некоторые
наркотические и возбуждающие агенты, такие, как пикротоксин или димфлин, действие которых основано на неспецифическом связывании с
внешним слоем мембран и изменении ионной проницаемости синаптических мембран (нервных синапсов).
Вторую группу составляют эффекторы, действие которых основано на изменении ими каталитического действия ферментов в результате
специфического взаимодействия эффектора с молекулой фермента.
Благодаря тому, что скорости обычных химических реакций намного ниже скоростей каталитических реакций, избирательность действие таких специфических эффекторов обеспечивает эффект "химического
усиления", благодаря которому всего несколько молекул эффектора существенным образом влияют на выход продукта в масштабах клетки.
Эффекторы ферментативных реакций принято разделять на ингибиторы и активаторы.
Ингибиторы разделяют на обратимые и необратимые.
Обратимые ингибиторы не вносят в молекулу фермента какихлибо изменений после своей диссоциации.
Необратимые ингибиторы необратимо модифицируют целевой
фермент.
Различают конкурентное, неконкурентное и бесконкурентное ингибирование.
Схема фермент-субстратного комплекса в отсутствии ингибирования представлена в таблице 9 (1).
Конкурентным называется ингибирование, при котором молекула
ингибитора подобна молекуле субстрата (аналог субстрата) (таблица 9 (2)). Она блокирует активный центр фермента и полностью предот237
вращает связывание фермента с субстратом. Субстрат и ингибитор конкурируют за место связывания на ферменте.
субстратом которой является янтарная кислота (рисунок 123(г)) (сукцинат), так как они сходны по строению с субстратом.
Таблица 9 – Схемы ингибирования
Схема фермент-субстратного
Тип регуляции
комплекса
1
В отсутствии
ингибирования
2
Конкурентное
ингибирование
а
б
в
г
Рисунок 123 – Схемы строения: а – малоновой; б – щавелево-уксусной; в – глутаровой и г – янтарной (сукцинат) кислот
3
Аналог переходного
состояния
4
Неконкурентное
ингибирование
5
Суицидные субстраты
Другой пример, сульфаниламидные антибактериальные препараты
(рисунок 124(а)) имеют сходное строение с парааминобензойной кислотой
(рисунок 124(б)) и являются конкурентными ингибиторами в синтезе бактериями фолиевой кислоты (фактора роста бактерий).
а
6
б
Рисунок 124 – Схемы строения: а – сульфаниламидных антибактериальных
препаратов; б – парааминобензойной кислоты
Аллостерическое
ингибирование
Аналоги переходного состояния (таблица 9(3)) также действуют как
конкурентные ингибиторы.
Например (рисунок 123), малоновая (а), щавелево-уксусная (б) и
глутаровая (в) кислоты ингибируют фермент сукцинатдегидрогеназу,
238
У человека нет такого метаболического пути и в лечебных дозах
они не влияют на жизнедеятельность человека, оказывая общий бактериостатический эффект (нарушая в некоторой степени деятельность кишечной микрофлоры).
Неконкурентным называется ингибирование, при котором связывание фермента с ингибитором не влияет на связывание фермента с суб239
стратом, но ингибитор модифицирует функционально важную каталитическую группу фермента "отключая" фермент. Структура активного
центра изменяется, и каталитическое превращение не происходит (таблица 9(4)).
Неконкурентные ингибиторы, поскольку они модифицируют функциональные группы целевого фермента, действуют, как правило, необратимо.
В случае так называемых "суицидных субстратов" речь идет о субстратных аналогах, содержащих дополнительно реакционную группу
(таблица 9(5)). Вначале они связываются обратимо, а затем образуют ковалентное соединение с активным центром фермента. Поэтому ингибирование такими соединениями проявляется как неконкурентное. Известным
примером такого ингибитора является антибиотик пенициллин.
Бесконкурентным называется ингибирование, которое возникает,
когда ингибитор может связываться с ферментом только в виде его комплекса с субстратом.
Кинетическая схема ингибирования выглядит следующим образом
E
KI 7
EI
Здесь: K I =
KS
↔
↔
αK S
ES → E + P
7 K I′
.
EIS
Таблица 10 – Возможные случаи общего процесса ингибирования
ферментов
Предельное
условие
α→∞
Тип ингибирования
Механизм ингибирования
Конкурентное ин- Связывание фермента с ингибитором
гибирование
предотвращает связывание с субстратом
α =1
Неконкурентное
ингибирование
Связывание фермента с ингибитором не
влияет на связывание с субстратом, но
предотвращает образование продукта
KI = ∞
Бесконкурентное
ингибирование
Ингибитор связывается с ферментом
только после образования фермент-субстратного комплекса и предотвращает
образование продукта
α ≠ 1, α ≠ ∞
KI ≠ ∞
Смешанное ингибирование
Общий случай
[ E ][ S ]
– константа диссоциации комплекса ES , в реакции
[ ES ]
↔ ES → E + P
Для конкурентного ингибирования α = ∞ :
↔
Для неконкурентного ингибирования α = 1 :
E
KI 7
EI
ES ↔ E + S ,
K I′ – константа диссоциации комплекса EIS в реакции
EIS ↔ ES + I ,
αK S – константа диссоциации комплекса EIS в реакции
KS
E ↔
Для бесконкурентного ингибирования K I = ∞ :
EIS ↔ EI + S .
240
KS
E
KI 7
EI
[ E ][ I ]
– константа диссоциации комплекса EI , в реакции
[ EI ]
EI ↔ E + I ,
KS =
Предельные случаи этой схемы представлены в таблице 10.
241
.
KS
ES → E + P
.
↔ EIS
KS
ES → → E + P
7 K I′
.
EIS
И, наконец, существует аллостерическое ингибирование.
Аллостерические ингибиторы связываются с отдельными участками фермента вне активного центра. Такое связывание влечет за собой
конформационные изменения в молекуле фермента, которые приводят к
уменьшению его активности (таблица 9(6)).
Аллостерические эффекты встречаются практически только в случае олигомерных ферментов.
Аллостерические эффекты могут заключатся как в ингибировании,
так и в активации фермента, поэтому аллостерическое ингибирование –
это частный случай аллостерического механизма регуляции.
Общепринятая классификация ингибиторов основана на их влиянии
1
1
).
от
на зависимость Лайнуивера-Берка (зависимость
w
[S ]
11.2. КОНКУРЕНТНОЕ ИНГИБИРОВАНИЕ
В случае конкурентного ингибирования
k1
k2
E + S → ES → E + P,
←
k−1
k3
E + I → EI ,
←
общая схема каталитической реакции имеет следующий вид:
k2
E ↔ ES → E + P.
KI
[ E ]0 [ S ]0 , [ E ]0 [ I ]0 .
Уравнения скоростей в стационарном состоянии будут иметь вид
d[ ES ]
= −(k−1 + k2 )[ ES ] + k1[ E ][ S ] = 0,
dt
d[ EI ]
= −k−3[ EI ] + k3[ E ][ I ] = 0.
dt
Откуда получаем
[ E ][ S ] k −1 + k 2
= K S – константа Михаэлиса для субстрата S ,
=
k1
[ ES ]
[ E ][ I ] k −3
=
= K I – константа диссоциации комплекса EI .
k3
[ EI ]
Подставляем в эти выражения для констант значение
[ E ] = [ E ]0 − [ ES ] − [ EI ] , которое следует из уравнения материального баланса [ E ]0 = [ E ] + [ ES ] + [ EI ] .
k−3
KS
субстратом. Поэтому концентрация комплекса ES понижена и скорость
d[ P ]
реакции w =
= k2 [ ES ] (пропорциональная [ES ] ) падает.
dt
В стационарном случае субстрат и ингибитор присутствуют в системе в избытке
7
EI
Образование комплекса EI является кинетическим "тупиком" – из
него не образуются продукты. Ингибитор выводит из реакции некоторое
количество свободного фермента, который теперь не может связываться с
242
Получаем
KS =
[ S ]([ E ]0 − [ ES ] − [ EI ])
,
[ ES ]
KI =
[ I ]([ E ]0 − [ ES ] − [ EI ])
.
[ EI ]
Из последнего выражения следует
[ EI ] =
[ I ]([ E ]0 − [ ES ])
.
K I + [I ]
243
Подставляем [EI ] в K S =
[ S ]([ E ]0 − [ ES ] − [ EI ])
[ ES ]
⎛
[ I ]([ E ]0 − [ ES ]) ⎞
[ S ] ⋅ ⎜ [ E ]0 − [ ES ] −
⎟
KI + [I ]
⎝
⎠=
KS =
[ ES ]
[ S ][ I ][ E ]0 − [ S ][ I ][ ES ]
[ S ][ E ]0 − [ S ][ ES ] −
KI + [I ]
.
=
[ ES ]
Откуда получаем
Берем обратные величины от обеих частей уравнения
1 K I [S ] + K S [ I ] + K I K S
1
K ⎛ K + [I ] ⎞ 1
=
=
+ S ⎜ I
,
⎟⋅
w
wmax K I [ S ]
wmax wmax ⎝ K I ⎠ [ S ]
⎛
1
1
[I ] ⎞ K S 1
⎟⋅
=
+ ⎜⎜1 +
.
w wmax ⎝
K I ⎟⎠ wmax [ S ]
Сравним это выражение (уравнение прямой в координатах
1
1
и
)
w [S ]
для конкурентного ингибирования с формулой Лайнуивера-Берка в отсутствие ингибирования
1
1
K
1
=
+ S ⋅
.
w wmax wmax [ S ]
K I K S [ ES ] + K S [ ES ][ I ] = K I [ S ][ E ]0 + [ S ][ E ]0[ I ] − K I [ S ][ ES ] −
−[ S ][ ES ][ I ] − [ S ][ I ][ E ]0 + [ S ][ I ][ ES ]
Очевидно, что для разных (но постоянных) значений концентрации
конкурентного ингибитора [ I ] = const зависимость скорости реакции от
или
K I K S [ ES ] + K S [ ES ][ I ] = K I [ S ][ E ]0 − K I [ S ][ ES ] .
Таким образом
[ ES ] =
K I [ S ][ E ]0
.
K S [ I ] + K I [S ] + K I K S
Скорость получения продукта
d[ P]
k2 K I [ S ][ E ]0
w=
= k2 [ ES ] =
.
dt
K I [S ] + K S [ I ] + K I K S
При достаточно больших концентрациях [S ] скорость реакции приближается к предельной максимальной скорости wmax = k 2 [E ]0 , поэтому
концентрации в координатах Лайнуивера-Берка будет выглядеть как семейство прямых, отсекающих на оси ординат одинаковый отрезок, рав1
ный
, причем угол наклона прямых будет тем больше, чем больше
wmax
[I ] (рисунок 125).
1
w
[ I ] = const − растёт
( wmax ) −1
1
[S ]
можем записать
w=
wmax K I [ S ]
.
K I [S ] + K S [I ] + K I K S
244
Рисунок 125 – Зависимости Лайнуивера-Берка в случае конкурентного ингибирования
245
Поскольку: (1) ингибитор и субстрат конкурируют друг с другом за
один и тот же участок связывания на молекуле фермента и (2) в обоих
случаях связывание является обратимым, то при достаточно большом избытке [S ] относительно [I ] практически весь фермент будет находиться
продукты своим присутствием в составе фермент-субстратного комплекса.
В стационарных условиях система кинетических уравнений имеет
вид
в комплексе ES и скорость реакции будет равна той же максимальной
предельной скорости ферментативной реакции wmax .
d[ ES ]
= −(k−1 + k2 )[ ES ] + k1[ E ][ S ] − k3[ ES ][ I ] + k−3[ EIS ] = 0,
dt
d[ EI ]
= k3[ E ][ I ] + k−1[ EIS ] − k−3[ EI ] − k1[ EI ][ S ] = 0,
dt
d[ EIS ]
= k1[ EI ][ S ] + k3[ ES ][ I ] − (k−1 + k−3 )[ EIS ] = 0,
dt
d[ P ]
= k2[ ES ].
dt
При пониженных концентрациях [S ] ингибитор выводит некоторое
количество фермента из сферы реакции в виде комплекса EI , так что
концентрация ES (и, следовательно, скорость реакции w ) понижается.
11.3. НЕКОНКУРЕНТНОЕ И СМЕШАННОЕ ИНГИБИРОВАНИЕ
Для неконкурентного ингибирования
k1
k2
Запишем уравнение материального баланса
E + S → ES → E + P,
←
[ E ]0 = [ E ] + [ ES ] + [ EI ] + [ EIS ]
k−1
k3
E + I → EI ,
←
в виде
k−3
[ E ] = [ E ]0 − [ ES ] − [ EI ] − [ EIS ] .
k1
EI + S → EIS ,
←
k−1
Определим константы диссоциации
k3
ES + I → EIS .
←
Кинетическая схема ферментативной реакции в случае неконкурентного ингибирования имеет вид:
KS
KI =
7K I
7
[ ES ][ I ]
,
[ EIS ]
KS =
k2
E ↔ ES → E + P.
KI
[ E ][ I ]
,
[ EI ]
KI =
k−3
KS =
EI ↔ EIS
[ E ][ S ]
,
[ ES ]
[ EI ][ S ]
.
[ EIS ]
KS
При неконкурентном ингибировании ингибитор не влияет на связывание субстрата с ферментом, но препятствует превращению субстрата в
246
Очевидно
[ EI ]
[E]
, откуда следует система уравнений
=
[ EIS ] [ ES ]
247
[ EIS ] =
w = k 2 [ ES ] =
[ ES ][ I ]
,
KI
=
([ E ]0 − [ ES ] − [ EI ] − [ EIS ])[ EIS ] = [ ES ][ EI ],
[ EI ] =
K S [ EIS ] K S [ ES ][ I ]
=
.
K I [S ]
[S ]
=
Подставляем во второе уравнение этой системы выражения для
[EI ] и [EIS ] из первого и третьего уравнений и решаем второе уравнение
k 2 [ E ]0 [S ]
=
K [ I ] [ I ][ S ]
K S + [S ] + S
+
KI
KI
wmax [ S ]
,
K [ I ] [ I ][ S ]
+
K S + [S ] + S
KI
KI
где
относительно [ES ]
⎛
K S [ ES ][ I ] [ ES ][ I ] ⎞ [ ES ][ I ]
K [ ES ][ I ]
−
= [ ES ] S
,
⎜ [ E ]0 − [ ES ] −
⎟
K I [S ]
KI ⎠ KI
K I [S ]
⎝
wmax = k 2 [ E ]0 .
Выражение для обратной скорости
далее
[ E ]0 − [ ES ] −
K S [ ES ][ I ] [ ES ][ I ]
K
−
= [ ES ] S ,
[S ]
K I [S ]
KI
откуда получаем
1
=
w
=
K I [ S ][ E ] 0 − K I [ S ][ ES ] − K S [ ES ][ I ] − [ ES ][ I ][ S ] = K S K I [ ES ] ,
K S K I [ ES ] + K I [ S ][ ES ] + K S [ ES ][ I ] + [ ES ][ I ][ S ] = K I [ S ][ E ] 0 ,
[ ES ]( K S K I + K I [ S ] + K S [ I ] + [ I ][ S ]) = K I [ S ][ E ]0 ,
откуда следует
K I [ S ][ E ]0
[ ES ] =
=
K S K I + K I [ S ] + K S [ I ] + [ I ][ S ]
=
[ S ][ E ]0
.
K [ I ] [ I ][ S ]
K S + [S ] + S +
KI
KI
Таким образом, выражение для скорости образования продукта
имеет вид
248
1
будет иметь вид
w
K S [ I ] [ I ][ S ]
+
KI
KI
=
wmax [ S ]
K S + [S ] +
KS 1
1
[I ] KS 1 [I ] 1
+
+
+
=
wmax [ S ] wmax K I wmax [ S ] K I wmax
⎛ [I ] ⎞ ⎛ 1
K 1 ⎞
= ⎜1 +
+ S
⎟=
⎟⋅⎜
⎝ K I ⎠ ⎝ wmax wmax [ S ] ⎠
K ⋅ K + KS ⋅[I ] 1 KI + [I ] 1
.
= S I
+
[S ]
K I ⋅ wmax
K I wmax
Таким образом, это выражение представляет собой уравнение прямой в координатах Лайнуивера-Берка.
Концентрация неконкурентного ингибитора определяет как наклон
K I + [I ] K S
), так и постоянный коэффициент
прямой (множитель
K I wmax
K I + [I ] 1
в уравнении прямой.
K I wmax
В присутствии постоянной концентрации неконкурентного ингибитора ( [ I ] = const ) изменение зависимости Лайнуивера-Берка состоит в
249
увеличении угла наклона прямых и увеличении величины отрезка, отсекаемого на оси ординат прямыми Лайнуивера-Берка.
При этом все прямые пересекаются в точке, лежащей на оси абсцисс (рисунок 126).
1
w
1
w
[ I ] = const − растёт
[ I ] = const − растёт
1
[S ]
Рисунок 127 – Зависимости Лайнуивера-Берка в случае смешанного ингибирования
1
[S ]
1
−
KS
Рисунок 126 – Зависимости Лайнуивера-Берка в случае неконкурентного ингибирования
Координаты этой точки определяются равенством
1
wmax
+
KS 1
= 0,
wmax [ S ]
следовательно,
11.4. МЕТОД ДИКСОНА
Метод Диксона позволяет определять константу диссоциации K I
даже при отсутствии информации об абсолютном значении концентрации
субстрата.
Для этого перепишем выражения Лайнуивера-Берка для конкурентного (см. стр. 245)
⎛ [I ] ⎞ KS 1
1
1
=
+ ⎜1 +
⎟⋅
w wmax ⎝ K I ⎠ wmax [ S ]
и неконкурентного (см. стр. 249) ингибирования
1
1
=−
.
[S ]
KS
Конкурентное и неконкурентное ингибирование представляют собой два крайних случая ингибирования. На практике, большинство ферментативных реакций принадлежат к промежуточному случаю.
При этом характерная точка пересечения прямых в координатах
Лайнуивера-Берка находится в "промежуточном" положении (рисунок 127).
250
1 ⎛ [I ] ⎞ ⎛ 1
K 1 ⎞
= ⎜1 +
+ S
⎟
⎟⋅⎜
w ⎝ K I ⎠ ⎝ wmax wmax [ S ] ⎠
в следующем виде:
• конкурентное ингибирование:
1
1 ⎛ KS ⎞
KS
=
+
1+
[I ] ,
⎜
⎟
w wmax ⎝ [ S ] ⎠ wmax K I [ S ]
• неконкурентное ингибирование:
1
1 ⎛ KS ⎞
1 ⎛ KS ⎞
=
+
⋅[I ].
1+
1+
⎜
⎟
w wmax ⎝ [ S ] ⎠ wmax K I ⎜⎝ [ S ] ⎟⎠
251
Эти уравнения служат основой для построения зависимости Диксо1
на – зависимости
от концентрации ингибитора [I ] при постоянной конw
центрации субстрата [S ] .
следовательно, точка пересечения прямых Диксона лежит на оси абсцисс
(рисунок 128).
1
w
В случае неконкурентного ингибирования прямые Диксона пересекаются в точке, определяемой равенством
1 ⎛
KS ⎞
1
⎜1 +
⎟+
wmax ⎝ [ S ]1 ⎠ wmax K I
[S ]2
⎛
KS ⎞
⎜1 +
⎟ ⋅[I ] =
[
S ]1 ⎠
⎝
=
[S ]1
1 ⎛
KS ⎞
1
⎜1 +
⎟+
wmax ⎝ [ S ]2 ⎠ wmax K I
⎛
KS ⎞
⎜1 +
⎟ ⋅ [ I ],
[
S ]2 ⎠
⎝
[I ]
− KI
Рисунок 128 – Зависимости Диксона для случая неконкурентного ингибирова-
откуда следует
ния
1
1
1
1
+
+
[I ] =
[I ],
[ S ]1 [ S ]1 K I
[ S ]2 [ S ]2 K I
1
1
1
1
,
−
[I ] −
[I ] =
[ S ]1 K I
[ S ]2 K I
[ S ]2 [ S ]1
В случае конкурентного ингибирования прямые Диксона (рисунок 129) пересекаются в точке, определяемой равенством
1 ⎛
KS ⎞
KS
1 ⎛
KS ⎞
KS
[I ] =
[I ]
⎜1 +
⎟+
⎜1 +
⎟+
wmax ⎝ [ S ]1 ⎠ wmax K I [ S ]1
wmax ⎝ [ S ]2 ⎠ wmax K I [ S ]2
⎛ 1
⎛ 1
1 ⎞
1 ⎞
−
−
⎜
⎟ ⋅[I ] = −KI ⎜
⎟,
S
S
S
S
[
]
[
]
[
]
[
]1 ⎠
⎝ 2
⎝ 2
1⎠
или
и, наконец,
1
1
1
1
+
⋅[I ] =
+
⋅[I ],
[ S ]1 K I [ S ]1
[ S ]2 K I [ S ]2
[I ] = −K I .
откуда следует
При этом значении концентрация равна
1
1 ⎛ KS ⎞
1
1+
=
+
w wmax ⎜⎝ [ S ] ⎟⎠ wmax K I
1 ⎛ KS ⎞
1
1+
=
−
wmax ⎜⎝ [ S ] ⎟⎠ wmax K I
[I ] = −K I .
⎛ KS ⎞
⎜1 + [ S ] ⎟ ⋅ [ I ] =
⎝
⎠
⎛ KS ⎞
⎜1 + [ S ] ⎟ ⋅ K I =
⎝
⎠
1 ⎛ KS ⎞
1 ⎛ KS ⎞
1+
1+
=
−
= 0,
⎜
⎟
wmax ⎝ [ S ] ⎠ wmax ⎜⎝ [ S ] ⎟⎠
252
Следовательно, абсцисса пересечения прямых Диксона, так же как и
в случае неконкурентного ингибирования, равна − K I .
Но в случае конкурентного ингибирования ордината этой точки
равна
1
1 ⎛
KS ⎞
KS
1
,
=
KI =
⎜1 +
⎟−
w
wmax ⎝ [ S ]1 ⎠ wmax K I [ S ]1
wmax
253
а не нулю, как в случае неконкурентного ингибирования (рисунок 128).
1
w
Ферменты проявляют оптимальную активность при разных рН (рисунок 131), что позволяет осуществлять тонкую регулировку путей метаболизма либо самим организмом, либо в результате внешних воздействий
на организм.
[S ]2
[ S ]1
1
wmax
− KI
[I ]
Рисунок 129 – Зависимости Диксона для случая конкурентного ингибирования
Таким образом, графическое построение зависимостей Диксона позволяют экспериментально определить K I .
11.5. РН-РЕГУЛЯЦИЯ СКОРОСТЕЙ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
Типичная зависимость ферментативной активности от рН описывается колоколообразной кривой, как показано, например, на рисунке 130
для фермента гистидазы.
Рисунок 131 – Зависимость активности ферментов от рН
Простейший механизм влияния рН заключается в том, что фермент
может существовать в трех ионных формах EH 22+ , EH + и E , из которых
только в одной форме фермент способен к связыванию субстрата и к каталитическому превращению.
Примем для определенности, что каталитически активной является
форма EH + . Зависимость ферментативной активности от рН рассмотрим
на примере схемы
K1
K2
EH 22+ ↔ EH + ↔ E ,
для которой константы диссоциации
Рисунок 130 – Активность фермента гистидаза в зависимости от рН при действии на субстрат гистидин
254
K1 =
[ EH + ][ H + ]
,
[ EH 22+ ]
255
K2 =
[ E ][ H + ]
[ EH + ]
и уравнение материального баланса
Далее, для [ EH + ] :
[ E ]0 = [ E ] + [ EH + ] + [ EH 22+ ]
представляют собой систему трех уравнений с тремя неизвестными.
Выразим из уравнения материального баланса
⎛
⎞
[ H + ]2 [ E ]0
⋅[H + ]
[ E ]0 [ H + ] − ⎜
+
+ 2 ⎟
[
]
[
]
+
+
K
K
K
H
H
1
⎝ 1 2
⎠
[ EH + ] =
=
K2 + [H + ]
[ E ] = [ E ]0 − [ EH + ] − [ EH 22+ ]
и подставим в выражение для K 2 :
([ E ]0 − [ EH + ] − [ EH 22+ ])[ H + ]
K2 =
,
[ EH + ]
K 2 [ EH + ] + [ EH + ][ H + ] = [ E ]0 [ H + ] − [ EH 22+ ][ H + ] ,
=
[ E ]0 [ H + ]K1K 2 + K1[ E ]0 [ H + ]2 + [ E ]0[ H + ]3 − [ E ]0 [ H + ]3
=
( K 2 + [ H + ])( K1K 2 + K1[ H + ] + [ H + ]2 )
=
[ E ]0 [ H + ]K1K 2 + K1[ E ]0 [ H + ]2
=
( K 2 + [ H + ])( K1K 2 + K1[ H + ] + [ H + ]2 )
=
( K 2 + [ H + ])[ E ]0 [ H + ]K1
.
( K 2 + [ H + ])( K1K 2 + K1[ H + ] + [ H + ]2 )
Таким образом, зависимость концентрации однократно протонированной
формы фермента ( [ EH + ] ) от концентрации протонов в системе имеет вид
следовательно,
[ EH + ] =
[ E ]0 [ H + ] − [ EH 22+ ][ H + ]
.
[ EH + ] =
K2 + [H + ]
Подставим это выражение [ EH + ] в уравнение для K1
K1 =
+
+
[ H ] [ E ]0[ H ] − [ EH 22+ ][ H + ]
,
[ EH 22+ ]
K2 + [H + ]
И, наконец,
[ E ] = [ E ]0 − [ EH + ] − [ EH 22+ ] =
= [ E ]0 −
= [ E ]0
откуда следует соотношение
K1K 2[ EH 22+ ] + K1[ EH 22+ ][ H + ] = [ H + ]2 [ E ]0 − [ EH 22+ ][ H + ]2 ,
K1[ E ]0 [ H + ]
[ E ]0 [ H + ]2
−
=
K1K 2 + K1[ H + ] + [ H + ]2 K1K 2 + K1[ H + ] + [ H + ]2
K1K 2 + K1[ H + ] + [ H + ]2 − K1[ H + ] − [ H + ]2
.
K1K 2 + K1[ H + ] + [ H + ]2
Следовательно, для непротонированного фермента
и получим зависимость концентрации дважды протонированной формы
фермента ( [ EH 22+ ] ) от кислотности системы
[ EH 22+ ] =
K1[ E ]0[ H + ]
.
K1K 2 + K1[ H + ] + [ H + ]2
[ E ] = [ E ]0
K1K 2
.
K1K 2 + K1[ H + ] + [ H + ]2
[ E ]0 [ H + ]2
.
K1K 2 + K1[ H + ] + [ H + ]2
256
257
[ EH 22+ ]
[ H + ]2
=
,
[ E ]0
K1K 2 + K1[ H + ] + [ H + ]2
+
+
[ EH ]
K1[ H ]
=
,
[ E ]0
K1K 2 + K1[ H + ] + [ H + ]2
[E]
K1K 2
=
.
[ E ]0 K1K 2 + K1[ H + ] + [ H + ]2
Таким образом, если считать, что с субстратом может связываться и
Отностиельное содержание
указанных форм
Относительная доля каждой из форм фермента имеет вид
)
,
0
– максимальная скорость ферментативной реакции, которая бы
где wmax
наблюдалась, если бы весь фермент находился в активной форме EH + , а
оставшийся множитель
K1[ H + ]
характеризует долю общеK1K 2 + K1[ H + ] + [ H + ]2
го количества фермента, находящуюся в форме EH + .
На рисунке 132(а) представлено относительное содержание EH 22+ ,
EH
+
и E форм фермента при K1 = 10
−5
и K 2 = 10
−10
формулам
[ EH 22+ ]
[ E ]0
=
+ 2
[H ]
,
K1K 2 + K1[ H + ] + [ H + ]2
[ EH + ]
K1[ H + ]
=
,
[ E ]0
K1K 2 + K1[ H + ] + [ H + ]2
[E]
K1K 2
=
.
[ E ]0 K1K 2 + K1[ H + ] + [ H + ]2
258
, рассчитанное по
E
pK2
0,5
0,0
3
4
5
6
7
8
9
10
11
12
pH
а
Отностиельное содержание
указанных форм
(
wmax [ H + ] =
0
wmax
K1[ H + ]
K1K 2 + K1[ H + ] + [ H + ]2
EH
pK1
катализировать его превращение способна только форма EH + фермента,
и поскольку максимальная скорость реакции wmax пропорциональна этой
концентрации, то колоколообразная форма зависимости активности фермента от рН (рисунок 130) объясняется уравнением
+
2+
EH2
1,0
pK1 pK2
2+
EH2
1,0
EH
E
+
0,5
0,0
3
4
5
6
7
8
9
10
11
12
pH
б
Рисунок 132 – Зависимость относительного содержания различных форм фермента от рН для двух случаев: а – К1 = 10–5, К2 = 10–10; б – К1 = 10–7, К2 = 10–8
Относительное содержание EH 22+ , EH + и E форм фермента при
K1 = 10 −7 и K 2 = 10 −8 представлено на рисунке 132(б).
Максимум колоколообразной кривой найдем, приравняв нулю производную
⎞
d ⎛
K1[ H + ]
= 0.
+ ⎜
+
+ 2 ⎟
d[ H ] ⎝ K1K 2 + K1[ H ] + [ H ] ⎠
259
′
⎛ a( x) ⎞ a′( x) ⋅ b( x) − b′( x) ⋅ a( x)
, то достаточно приравПоскольку ⎜
⎟ =
(b( x)) 2
⎝ b( x ) ⎠
нять числитель нулю, то есть решить уравнение
K1 ( K1 K 2 + K1[ H + ] + [ H + ]2 ) − K1[ H + ]( K1 + 2[ H + ]) = 0
или
следовательно,
K1K 2[ H + ]оптим + K1[ H + ][ H + ]оптим + [ H + ]2 [ H + ]оптим =
2
,
= 2[ H + ]K1K 2 + 2[ H + ]K1[ H + ]оптим + 2[ H + ][ H + ]оптим
далее
K1K 2 [ H + ]оптим − K1[ H + ][ H + ]оптим + [ H + ]2 [ H + ]оптим −
2
− 2[ H + ]K1K 2 − 2[ H + ][ H + ]оптим
= 0.
K1 K 2 − [ H + ] 2 = 0 .
Таким образом, положение максимума кривой
[ H + ][ EH + ]
max
= K1K 2 = [ H + ]оптим .
Поскольку
(
)
2
Учитывая K1K 2 = [ H + ]оптим , получаем
2
[ H + ]3оптим − K1[ H + ][ H + ]оптим + [ H + ]2 [ H + ]оптим − 4[ H + ][ H + ]оптим
=0
и, сокращая [ H + ]оптим ,
1
1
pH оптим = − lg[ H + ]оптим = − (lg K1 + lg K 2 ) = (pK1 + pK 2 ) ,
2
2
то максимум колоколообразной кривой расположен при рН на середине
отрезка между рК1 и рК2 (рисунок 132).
Максимальное значение равно
⎛ [ EH + ] ⎞
K1[ H + ]оптим
=
.
⎜
⎟
+
+ 2
⎝ [ E ]0 ⎠max K1K 2 + K1[ H ]оптим + [ H ]оптим
Область рН, при которых активность фермента составляет более половины максимального значения, определим из условия
1
K1[ H + ]оптим
K1[ H + ]
=
,
2
2 K1K 2 + K1[ H + ]оптим + [ H + ]оптим
K1K 2 + K1[ H + ] + [ H + ]2
[ H + ]оптим ( K1K 2 + K1[ H + ] + [ H + ]2 ) =
2
),
= 2[ H + ]( K1K 2 + K1[ H + ]оптим + [ H + ]оптим
260
2
[ H + ]оптим
− K1[ H + ] + [ H + ]2 − 4[ H + ][ H + ]оптим = 0 ,
получим
(
)
2
[ H + ]2 − K1 + 4[ H + ]оптим ⋅ [ H + ] + [ H + ]оптим
= 0.
Корни этого уравнения дают значения [ H + ] , между которыми активность фермента превышает половину своего максимального значения.
11.6. АЛЛОСТЕРИЧЕСКАЯ РЕГУЛЯЦИЯ СКОРОСТЕЙ
ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
Субъединичная четвертичная структура аллостерических ферментов способствует повышению чувствительности системы и усилению обратной связи в механизмах регулирования. Такая структура способствует
увеличению чувствительности системы, так что малое изменение концентрации субстрата сильно влияет на скорость ферментативной реакции.
261
При этом характерный гиперболический ход зависимости скорости
ферментативной реакции от концентрации субстрата сменяется сигмоидной зависимостью. Так, например, на рисунке 133 схематически представлено изменение вида зависимости w от [S ] в ферментативной
реакции, происходящей под действием: (1) одиночной каталитической
единицы фермента аспартаттранскарбамилазы на субстрат аспартат
(кривая 1), и (2) под действием ассоциированного фермента, состоящего
из двух каталитических и трех регуляторных полипептидных субъединиц (кривая 2).
нии (relaxed, "расслабленное") и T -состоянии (tense, "напряженное").
Конформация R обладает высоким сродством к субстрату, а T – низким
(рисунок 134). Формы R и T могут переходить одна в другую.
В данной модели делается важное допущение, что для сохранения
симметрии димера обе субъединицы должны находиться в одном и том
же конформационном состоянии. То есть, разрешены состояния RR и TT ,
а состояние RT запрещено.
Рисунок 134 – Модель согласованного механизма аллостерических взаимодействий
Рисунок 133 – Зависимость скорости появления продукта от концентрации субстрата (аспартата)
Предложено много механизмов, объясняющих кинетические особенности аллостерических ферментов.
Обозначим [ R0 ] и [T0 ] – концентрации соответствующих форм, с
которыми не связаны молекулы субстрата, и L – константа аллостерического равновесия реакции R ↔ T в отсутствии субстрата. Тогда
L=
[T0 ]
[ R0 ]
Согласованный механизм аллостерических взаимодействий.
В 1965 г. Жак Моно, Джефри Уайман и Жан-Пьер Шанже предложили
объяснение кооперативности аллостерических эффектов в реакции связывания кислорода с гемоглобином.
Используя их подход, рассмотрим аллостерический фермент, состоящий из двух идентичных субъединиц, каждая с одним активным центром. Субъединицы могут находиться в двух конформациях – R -состоя-
Сделаем ещё одно допущение: пусть субстрат может присоединяться только к R -форме фермента. R -форму, связанную с одной молекулой
262
263
или
[T0 ] = L[ R0 ] .
субстрата обозначим R1 , а связанную с двумя молекулами субстрата – R2 .
Присоединение каждой молекулы субстрата характеризуется одной и той
же микроскопической константой диссоциации K R в реакциях
R0 + S ↔ R1 ,
R1 + S ↔ R2 .
Поскольку субстрат может связываться с любым из двух активных
центров на R0 и, с другой стороны, отщепляться от любого из двух активных центров на R2 , то константу диссоциации можно записать с одной
стороны в виде
KR =
2[ R0 ][ S ]
[ R1 ]
(или R1 =
Получим
⎛ [S ] ⎞
[ R0 ][ S ]
+ 2[ R0 ] ⋅ ⎜
⎟
KR
⎝ KR ⎠
где α =
[S ]
.
KR
В общем случае, если n – число субъединиц в молекуле фермента,
то доля Y активных центров занятых субстратом описывается уравнением
(без вывода)
2[ R0 ][ S ]
),
KR
а с другой стороны, в виде
KR =
[ R1 ][ S ]
2[ R2 ]
(или R2 =
Y=
[ R1 ][ S ]
).
2K R
Определим степень насыщения фермента Y , то есть число активных центров с присоединенными молекулами субстрата, отнесенное к
общему числу субстрат-связывающих центров
Y=
KR
[T ][ S ]
и (в общем случае) K T =
– константа диссоциации
KT
[TS ]
T -формы.
Зависимость Y от [ S ] выражается сигмоидной, а не гиперболиче-
скорости реакции от концентрации субстрата также будет сигмоидным,
поскольку
Подставим в это выражение соотношения
[T0 ] = L[ R0 ] ,
w = Y ⋅ wmax .
2[ R0 ][ S ]
,
KR
2
⎛ [S ] ⎞
[ R ][ S ] 2[ R0 ][ S ] [ S ]
⎟⎟ .
[ R2 ] = 1
=
= [ R0 ]⎜⎜
2K R
K R 2K R
⎝ KR ⎠
264
где c =
L ⋅ α ⋅ c ⋅ (1 + c ⋅ α) n−1 + α ⋅ (1 + α) n−1
,
L ⋅ (1 + c ⋅ α) n + (1 + α) n
ской кривой (рисунок 135).
Если число оборотов в расчете на один активный центр одинаково
для фермент-субстратных комплексов с R1 и R2 , то график зависимости
[ R1 ] + 2[ R2 ]
.
2([T0 ] + [ R0 ] + [ R1 ] + [ R2 ])
[ R1 ] =
2
[S ]
1+
[S ]
KR
Y=
=
⋅
=
2
2⎞
K
⎛
⎛ [S ] ⎞
R
⎛ [S ] ⎞
2[ R0 ][ S ]
L + ⎜1 +
2 ⎜ L[ R0 ] + [ R0 ] +
+ [ R0 ] ⋅ ⎜
⎟
⎟ ⎟
⎜
KR
⎝ KR ⎠
⎝ K R ⎠ ⎟⎠
⎝
1+ α
,
= α⋅
2
L + (1 + α )
2
Рассмотрим процесс связывания. В отсутствие субстрата почти все
молекулы фермента находятся в T -форме. В примере, показанном на ри-
265
сунке 135, на 105 молекул в T -форме приходится только одна молекула в
5
Степень насыщения Y
R -форме ( L = 10 ).
Добавление субстрата сдвигает конформационное равновесие в
сторону образования R -формы, поскольку именно R -форма связывает
субстрат. Когда субстрат присоединяется к одному активному центру,
второй активный центр должен быть также в R -форме, согласно основному постулату данной модели.
+ Активатор
1,0
L=10
0,8
3
L=10
0,6
4
0,4
L=10
+ Ингибитор
0,2
0,0
5
0
1x10
-3
2x10
-3
-3
сутствии ингибитора и повышается в присутствии активатора.
Рассмотренное ранее неконкурентное ингибирование можно рассматривать как аллостерическое торможение.
Среди аллостерических взаимодействий различают гомотропные
(взаимодействия между идентичными лигандами) и гетеротропные
(взаимодействия между различными лигандами).
В рассмотренной модели кооперативное связывание субстрата ферментом представляет собой гомотропный эффект, а влияние активатора
или ингибитора – гетеротропный. При согласованном механизме аллостерических взаимодействий гомотропные эффекты всегда положительны (кооперативны), а гетерогенные могут быть и положительными и
отрицательными.
3x10
Концентрация [S], M
Рисунок 135 – Зависимость степени насыщения активных центров фермента от
концентрации субстрата в модели согласованного механизма аллостерических взаимодействий при KR = 10–5 M
Другими словами, переход от T к R и обратно все субъединицы
фермента осуществляют согласованно. Следовательно, по мере добавления субстрата доля молекул фермента в R -форме прогрессивно возрастает, и связывание субстрата происходит кооперативно.
Предложенная модель согласованного механизма объясняет влияние аллостерических ингибиторов и активаторов. Аллостерический ингибитор связывается преимущественно с T -формой, тогда как
266
аллостерический активатор связывается преимущественно с R -формой.
Аллостерический ингибитор сдвигает конформационное равновесие
R ↔ T в сторону T , а аллостерический активатор – в сторону R . Эти эффекты можно выразить количественно через изменение константы аллостерического равновесия L . Аллостерический ингибитор повышает
величину L , тогда как аллостерический активатор понижает её. Эти эффекты показаны на рисунке 135.
Степень насыщения Y при всех значениях [ S ] снижается в при-
Последовательный механизм аллостерических взаимодействий.
Даниэль Кошланд разработал другую модель – последовательный механизм аллостерических взаимодействий (рисунок 136).
В основу модели Кошланда основу положены три постулата.
1. Каждая субъединица может существовать в одном из двух
возможных конформационных состояний ( R или T ).
2. Связывание субстрата изменяет форму той субъединицы, к
которой он присоединяется. Конформация другой субъединицы при
этом существенно не меняется.
3. Конформационные изменения, вызванные связыванием субстрата на одной субъединице, могут увеличивать или уменьшать
сродство к субстрату другой субъединицы той же молекулы фермента.
267
Связывание является кооперативным, если у RT -формы сродство к
субстрату выше, чем у TT -формы.
Модель простого последовательного механизма взаимодействия
отличается от модели согласованного механизма в нескольких отношениях.
11.7. АВТОИНГИБИРОВАНИЕ СУБСТРАТОМ
Другим средством регуляции скорости ферментативной реакции является торможение реакции при высокой концентрации субстрата, как это
имеет место в случае разложения мочевины уреазой (рисунок 137).
Рисунок 136 – Модель последовательного механизма кооперативного связывания субстрата аллостерическим ферментом
Во-первых, в отсутствие субстрата весь фермент находится в T форме. Переход от T -формы к R -форме индуцируется присоединением
субстрата.
Во-вторых, конформационный переход от T к R в разных субъединицах фермента происходит не согласованно, а последовательно. В модели согласованного механизма, напротив, наличие гибридной формы RT
исключается. Модель согласованного механизма исходит из важной роли
симметрии во взаимодействии субъединиц в олигомерных белках и потому предполагает её сохранение при аллостерических переходах.
В-третьих, в случае согласованного механизма гомотропные взаимодействия всегда должны быть положительными, тогда как в случае
последовательного механизма они могут быть либо положительными, либо отрицательными. Это зависит от структурных переходов, вызванных
присоединением первой молекулы субстрата.
Обе модели используются для описания различных аллостерических белков. Однако существуют аллостерические белки, для описания
которых требуются более сложные модели.
Рисунок 137 – Автоингибирование субстратом реакции разложения мочевины
уреазой: 1 – ожидаемая гиперболическая кривая в отсутствие ингибирования; 2 – экспериментальные данные, свидетельствующие о усилении ингибирования при повышенных концентрациях субстрата
Механизм этого процесса заключается в том, что связывание данного фермента со второй молекулой субстрата эффективно препятствует
осуществлению биокаталитической реакции:
k1
k2
E + S → ES → E + P ,
←
k−1
k3
ES + S → ES2 → реакции нет .
←
k−3
Схематически такая модель автоингибирования реакции при высокой концентрации субстрата представлена на рисунке 138.
268
269
нуивера-Берка в координатах
1
1
при очень малых концентрациях
,
w [S ]
субстрата [S ] .
а
б
1
w
Рисунок 138 – Схема ингибирования избытком субстрата: а – нормальное связывание субстрата S с ферментом E, превращение возможно; б – аномальное связывание, ни один из субстратов не превращается в продукт.
wK S′
Очевидное подобие этого механизма рассмотренной выше схеме
K1
1
wmax
K2
рН-регуляции EH 22+ ↔ EH + ↔ E позволяет нам использовать полученное
K S′
wmax K S′ [ S ]
,
[ S ] + K S′ [ S ] + K S K S′
субстратных комплексов ES и ES 2 : (вместо K1 =
График зависимости w =
[ EH + ][ H + ]
используем
[ EH 22+ ]
wmax K S′
[ ES ][ S ]
[ E ][ H ]
[ E ][ S ]
, вместо K 2 =
используем K S =
).
[ ES2 ]
[ ES ]
[ EH + ]
wmax K S′ [ S ]
wmax
wmax
w K′
=
=
≈ max S .
2
K
S
[
]
K S′ + [ S ]
K ′ [ S ] K S K S′ 1 + S +
[ S ] + K S′ [ S ] + K S K S′
[S ]
+ S
+
[ S ] K S′
K S′ [ S ] K S′ [ S ] K S′ [ S ]
2
1
, [ S ] (рисуw
определяют из обычной зависимости Лай-
Величину K S′ определяем из графика в координатах
нок 139). Величины K S и wmax
270
wmax K S′ [ S ]
, так же как и в случае
[ S ] + K S′ [ S ] + K S K S′
2
рН-регулирования, имеет колоколообразный вид. Максимум колоколообразной кривой находим, приравняв нулю производную
+
При высоких концентрациях субстрата
w=
Рисунок 139 – Зависимости 1/w от [S] для ферментативной реакции, ингибируемой высокой концентрацией субстрата
2
где вместо констант диссоциации для случая ионных форм фермента используем константы диссоциации моно- и бисубстратных фермент-
K S′ =
[S ]
KS
выше выражение для скорости реакции ES 2 ↔ ES ↔ E
w=
тангенс угла наклона
1 прямой
d ⎛
[S ]
⎜
d[ S ] ⎝ [ S ]2 + K S′ [ S ] + K S K S′
⎞
⎟=0
⎠
′
⎛ a ( x) ⎞ a′( x) ⋅ b( x) − b′( x) ⋅ a ( x)
⎟⎟ =
, то достаточно решить
Поскольку ⎜⎜
(b( x)) 2
⎝ b( x ) ⎠
уравнение
[ S ]2 + K S′ [ S ] + K S K S′ − [ S ]( K S′ + 2[ S ]) = 0
или
K S K S′ − [ S ]2 = 0 .
271
Откуда положение максимума кривой
зависимости Лайнуивера-Берка (зависимость
[ S ]wmax = K S K S′ .
Таким образом, в рассматриваемом механизме автоингибирования
(самоторможения) субстратом скорость реакции увеличивается при увеличении концентрации субстрата, но в присутствии избытка субстрата
скорость падает, обеспечивая простое средство прямой регуляции скорости образования продукта.
ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОКОНТРОЛЯ
1. Какие химические соединения называются эффекторами?
2. Назовите две группы внешних регуляторов ферментативных реакций.
3. В чем отличие обратимого и необратимого ингибирования?
4. В чем отличие конкурентного и неконкурентного ингибирования?
5. Какие субстраты называются суицидными?
6. Запишите общую схему каталитической реакции в присутствии
ингибитора.
7. Для случая конкурентного ингибирования каталитической реакk3
k1
k−3
k−1
k2
ции EI → E + S + I → ES → E + P , показать, что при стационарных
←
←
условиях выражение для скорости изменения концентрации
wmax K I [ S ]
k + k2
, где K S = −1
продукта имеет вид w =
K I [S ] + K S [ I ] + K I K S
k1
и KI =
k −3
.
k3
8. Для случая конкурентного ингибирования каталитической реакk3
k1
k−3
k−1
k2
ции EI → E + S + I → ES → E + P , показать, что в присутствии по←
←
стоянной
концентрации
ингибитора
272
[ I ] = const
изменение
1
1
) состоит
от
w
[S ]
в увеличении угла наклона прямых при неизменной величине
отрезка, отсекаемого на оси ординат.
9. Запишите координаты точки, в которой пересекаются прямые
Лайнуивера-Берка в случае конкурентного ингибирования?
10. Для случая неконкурентного ингибирования каталитической реакции показать, что при стационарных условиях выражение для
скорости изменения концентрации продукта имеет вид
K
1 ⎛
[I ] ⎞ ⎛ 1
1 ⎞
[ E ][ I ]
[ E ][ S ]
⎟⎟ , где K I =
⎟⎟ ⋅ ⎜⎜
и KS =
,
= ⎜⎜1 +
+ S
[ EI ]
[ ES ]
w ⎝
K I ⎠ ⎝ wmax wmax [ S ] ⎠
[ I ] и [ S ] – концентрации ингибитора и субстрата, соответствен-
но.
11. Для случая неконкурентного ингибирования каталитической реакции, выражение для скорости образования продукта которой
имеет вид
KI =
K 1 ⎞
1 ⎛ [I ] ⎞ ⎛ 1
[ S ][ E ]
⎟⎟ (где K S =
⎟⎟ ⋅ ⎜⎜
= ⎜⎜1 +
+ S
и
w ⎝
K I ⎠ ⎝ wmax wmax [ S ] ⎠
[ ES ]
[ E ][ I ]
– константы диссоциации комплексов ES и EI , со[ EI ]
ответственно), показать, что в присутствии постоянной концентрации неконкурентного ингибитора [ I ] = const изменение
зависимости Лайнуивера-Берка (зависимость
1
1
) состоит
от
w
[S ]
в увеличении угла наклона прямых при неизменной величине
отрезка, отсекаемого на оси абсцисс.
12. Запишите координаты точки, в которой пересекаются прямые
Лайнуивера-Берка в случае неконкурентного ингибирования?
13. В чем заключается преимущество метода Диксона?
14. Для случая неконкурентного ингибирования каталитической реакции показать, как методом Диксона определить значение кон[ E ][ I ]
станты K I =
диссоциации комплекса EI .
[ EI ]
273
15. Для случая конкурентного ингибирования каталитической реакции показать, как методом Диксона определить значение кон[ E ][ I ]
диссоциации комплекса EI .
станты K I =
[ EI ]
16. Сформулируйте простейший механизм, объясняющий колоколообразную форму зависимости ферментативной активности от
рН.
17. Для случая зависимости ферментативной активности от рН
K1
K2
EH 22+ ↔ EH + ↔ E , в которой только форма EH + является
каталитически активной, показать, что зависимость активности
фермента от рН описывается уравнением
wmax =
0
wmax
K1 [ H + ]
.
K 1 K 2 + K1 [ H + ] + [ H + ] 2
18. Для случая зависимости ферментативной активности от рН
K1
K2
EH 22+ ↔ EH + ↔ E , в которой только форма EH + является ката-
литически активной, и зависимость активности фермента от рН
описывается уравнением wmax =
0
wmax
K1[ H + ]
K1 K 2 + K1[ H + ] + [ H + ] 2
пока-
зать, что максимум кривой расположен при [ H + ]оптим = K1 K 2 .
19. Как изменяется ход зависимости скорости ферментативной реакции от концентрации субстрата в случае аллостерической регуляции ферментативной активности?
20. В чем специфика согласованного механизма аллостерических
взаимодействий?
21. В чем отличие гомотропных и гетеротропных аллостерических
взаимодействий?
22. Чем отличается модель простого последовательного механизма
взаимодействия от модели согласованного механизма?
23. В чем заключается механизм автоингибирования субстратом?
24. Как определяют константу диссоциации K S′ в случае автоингибирования субстратом?
274
Глава 12
ФЕРМЕНТАТИВНЫЕ РЕАКЦИИ В НЕСТАЦИОНАРНОМ
РЕЖИМЕ
12.1. НЕСТАЦИОНАРНАЯ КИНЕТИКА ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
Кинетические исследования ферментативных реакций, протекающих в стационарных условиях, обычно позволяют определить только два
параметра: константу Михаэлиса и максимальную скорость реакции. Поэтому стационарная кинетика может дать лишь предварительную информацию о детальном кинетическом механизма ферментативной реакции.
Стационарная кинетика отражает лишь лимитирующие стадии процесса
и практически не дает информации о быстрых, нелимитирующих стадиях
превращения субстрата в активном центре фермента.
Для того чтобы зарегистрировать промежуточные "короткоживущие" соединения и измерить константы скорости отдельных стадий необходимо измерить скорость приближения системы к стационарному
состоянию. Индивидуальные константы скорости могут быть измерены за
промежуток времени, в течение которого устанавливается это состояние.
Характерные времена установления равновесия 1–10–7 с. Для работы в таком предстационарном интервале времен требуется аппаратура
для быстрого смешивания и последующего наблюдения за ферментом и
субстратом. Кроме того, поскольку наблюдаемые события происходят на
самом ферменте, то на первый взгляд может показаться, что этот фермент должен присутствовать в количествах, сравнимых с количеством
субстрата. Однако детальный экспериментальный и теоретический анализ
показал, что в случае избытка концентрации фермента по сравнению с
субстратом, стационарное состояние не устанавливается. Если же в системе изначально присутствует избыток субстрата, то начальное нестационарное протекание реакции выходит затем на стационарный режим.
В этом смысле такую кинетику принято называть предстационарной.
В качестве примера рассмотрим схему ферментативной реакции с
участием одного промежуточного соединения
275
k1
k2
k−1
k−2
E + S → ES → E + P .
← ←
Чтобы найти предэкспоненциальный множитель C , продифференцируем выражение [ ES ] = C exp[−(k1[ S ]0 + k −1 + k 2 )t ]
d[ ES ]
= −(k1[ S ]0 + k−1 + k2 ) ⋅ C exp [ −(k1[ S ]0 + k−1 + k2 )t ]
dt
Кинетика данной реакции описывается системой уравнений:
d[ ES ]
= k1[ E ][ S ] − (k−1 + k2 )[ ES ] + k−2[ E ][ P] ,
dt
d[ P]
w=
= k2 [ ES ] − k−2 [ E ][ P ] ,
dt
[ E ]0 = [ E ] + [ ES ] ,
и подставим в уравнение
ченное выражение
−(k1[ S ]0 + k−1 + k2 ) ⋅ C exp [ −(k1[ S ]0 + k−1 + k2 )t ] +
[ S ]0 = [ S ] + [ ES ] + [ P] .
+ (k1[ S ]0 + k−1 + k2 )[ ES ] = k1[ E ]0[ S ]0 ,
Решение этой нелинейной системы уравнений можно существенно
упростить, если использовать некоторые условия экспериментального характера, позволяющие привести дифференциальные уравнения к линейному виду.
При большом избытке субстрата ( [ S ]0 [ E ]0 ) [ S ] ≈ [ S ]0 и неболь-
[ ES ] =
Подставляем [ E ] = [ E ]0 − [ ES ] в первое уравнение, переносим в левую часть члены с [ ES ] и получаем первое уравнение в виде
d[ ES ]
+ (k1[ S ]0 + k−1 + k2 )[ ES ] = k1[ E ]0[ S ]0 .
dt
Решение этого неоднородного уравнения имеет вид (без вывода)
[ ES ] = C exp[−(k1[ S ]0 + k −1 + k 2 )t ] .
276
k1[ E ]0 [ S ]0
+ C exp [ −(k1[ S ]0 + k−1 + k2 )t ] .
k1[ S ]0 + k−1 + k2
С учетом начальных условий ( [ ES ]0 = 0 при t = 0 ) получим:
C=−
шой глубине реакции ( [ P] ≈ 0 ) систему можно записать в виде
d[ ES ]
= k1[ E ][ S ]0 − (k−1 + k2 )[ ES ] ,
dt
d[ P]
= k2 [ ES ] ,
dt
[ E ]0 = [ E ] + [ ES ] .
d[ ES ]
+ (k1[ S ]0 + k−1 + k2 )[ ES ] = k1[ E ]0[ S ]0 полуdt
k1[ E ]0 [ S ]0
,
k1[ S ]0 + k −1 + k 2
откуда
[ ES ] =
k1[ E ]0[ S ]0
k1[ E ]0[ S ]0
exp [ −(k1[ S ]0 + k−1 + k2 )t ] .
−
k1[ S ]0 + k−1 + k2 k1[ S ]0 + k−1 + k2
После несложных преобразований, разделив числители и знаменатели в
дробях на k1 и вынеся k1 за скобки в выражении под экспонентой, получим
[ ES ] =
=
[ E ]0[ S ]0
k +k
[ S ]0 + −1 2
k1
⎛
⎧ ⎛
k + k ⎞ ⎫⎞
⎜⎜1 − exp ⎨−k1 ⎜ [ S ]0 + −1 2 ⎟ ⋅ t ⎬ ⎟⎟ =
k1 ⎠ ⎭ ⎠
⎩ ⎝
⎝
[ E ]0 [ S ]0
1 − exp {−k1 ([ S ]0 + K M ) ⋅ t} .
K M + [ S ]0
(
)
277
Как видно из последнего уравнения (рисунок 140(а)), концентрация
фермент-субстратного комплекса [ES ] возрастает со временем и стремит-
го комплекса имеет вид
ся к пределу
[ ES ] =
[ ES ]стац =
[ E ]0[ S ]0
,
K M + [ S ]0
[ E ]0 [S ]0
(1 − exp{−k1 K M ⋅ t}) .
KM
12.2. ОПРЕДЕЛЕНИЕ КОНСТАНТ СКОРОСТЕЙ ИЗ НЕСТАЦИОНАРНОЙ
КИНЕТИКИ
а само уравнение можно записать в виде
(
Из кинетики накопления фермент-субстратного комплекса [ES ]
)
[ ES ] = [ ES ]стац 1 − exp {−k1 ([ S ]0 + K M ) ⋅ t} .
может быть найдена константа скорости k1 и сумма констант скоростей
(k −1 + k 2 ) . Для этого введем функцию τ
а
[ES]/[E]0
1
б
[S]0
в
1
[S]0
τ
= k1[ S ]0 + k −1 + k 2
0,5[S]0
0,25[S]0
0,5[S]0
0,25[S]0
Тогда из уравнения [ ES ] =
получим
⎛
⎛ t ⎞⎞
[ ES ] = [ ES ]стац ⎜1 − exp ⎜ − ⎟ ⎟ .
⎝ τ ⎠⎠
⎝
Время, t
Рисунок 140 – Зависимость концентрации промежуточного соединения от времени в предстационарном режиме
Логарифмируем это соотношение
При [ S ]0 K M (рисунок 140(б)) зависимость от времени концен[ E ]0 [S ]0
(1 − exp{−k1 ([ S ] 0 + K M ) ⋅ t}) фермент-субстратнотрации [ ES ] =
K M + [S ]0
го комплекса имеет вид
[ ES ] = [ E ] 0 (1 − exp{−k1 [ S ] 0 ⋅ t}) .
При [ S ]0 K M (рисунок 140(в)) зависимость от времени концентрации [ ES ] =
[ E ]0 [S ]0
(1 − exp{−k1 ([ S ] 0 + K M ) ⋅ t}) фермент-субстратноK M + [S ]0
278
[ E ]0 [S ]0
(1 − exp{−k1 ([ S ] 0 + K M ) ⋅ t})
K M + [S ]0
t
ln([ ES ]стац − [ ES ]) = ln[ ES ]стац − ,
τ
и получаем
⎛
[ ES ] ⎞
t
1
ln ⎜1 −
⎟ = − = − ⋅t .
[
ES
]
τ
τ
стац ⎠
⎝
⎛
[ ES ] ⎞
Это выражения – уравнение прямой в координатах ln ⎜1 −
⎟ и t.
⎝ [ ES ]стац ⎠
279
По тангенсу угла наклона этой прямой определяем
Поскольку
1
τ
1
τ
.
= k1[ S ]0 + k −1 + k 2 , то если провести эксперименты при
различных начальных концентрациях субстрата [ S ]0 и определить для
каждого значения [ S ]0 величину
1
τ
, то можно построить график прямой в
1
координатах ( , [ S ]0 ), и найти k1 , как тангенс угла наклона этой прямой
τ
1
τ
нок 141).
тангенс угла наклона
прямой= k1
k−1 + k2
[S ]0
Рисунок 141 – Определение элементарных констант из данных по предстационарной кинетике ферментативной реакции.
Из полученной таким способом величины суммы (k −1 + k 2 ) можно
рассчитать величину k −1 , поскольку константу k 2 легко определить из
стационарной кинетики реакции, в которой wmax = k2 [ E ]0 .
280
При изучении любых проблем химической кинетики одним из основных теоретических положений является уравнение Аррениуса, выражающее зависимость константы скорости реакции от температуры
⎛ Ε ⎞
k = A exp⎜ − a ⎟ ,
⎝ RT ⎠
где Ε a – энергия активации реакции; R – универсальная газовая постоянная; A – предэкспоненциальный множитель; T – абсолютная температура.
= k1[ S ]0 + k −1 + k 2
и (k −1 + k 2 ) , как отрезок, отсекаемый этой прямой на оси ординат (рису-
1
τ
12.3. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ РЕАКЦИЙ
⎛1⎞
График зависимости Аррениуса в координатах (ln k ) от ⎜ ⎟ пред⎝T ⎠
⎛ Ε ⎞
ставляет собой прямую с тангенсом угла наклона равным ⎜ − a ⎟ .
⎝ R ⎠
Многие реакции, катализируемые ферментами, подчиняются аррениусовской зависимости константы скорости реакции от температуры.
Например, на рисунке 142 представлены экспериментальные данные и
линейная аппроксимация температурной зависимости скорости ферментативной реакции гидролиза АТФ миозином.
Отметим, что температурный диапазон, в котором были получены
данные, представленные на рисунке 142, является очень узким и охватывает только диапазон физиологически приемлемых температур.
В этом эксперименте не рассматривались температуры, значительно
превышающие обычные в биологических условиях пределы. Попытка
поднять температуру значительно выше указанного диапазона приводит к
денатурации белковых молекул.
Денатурация большинства белков начинается в диапазоне темпера-
тур от 45–50°С и завершается очень быстро при 55°С (исключение составляют ферменты термофильных микроорганизмов, обитающих в
горячих источниках, они сохраняют стабильность до 80–85°С).
281
active) E inact и активная (active) E act формы фермента находятся в равновесии
Eact R Einact
Константу равновесия K d этой реакции (d – денатурация (denaturation)) можно выразить следующим уравнением
[ E ]inact
⎛ ΔG ⎞
⎛ ΔH d ⎞
⎛ ΔS d ⎞
= K d = exp ⎜ − d ⎟ = exp ⎜ −
⎟ ⋅ exp ⎜
⎟.
[ E ]act
⎝ RT ⎠
⎝ RT ⎠
⎝ R ⎠
где ΔG d , ΔH d и ΔS d – свободная энергия, энтальпия и энтропия инактивации соответственно.
Рисунок 142 – Аррениусовская зависимость от температуры скорости ферментативной реакции гидролиза АТФ миозином
Пример инактивации фермента каталаза при повышении температуры представлен на рисунке 143.
Один из механизмов термической денатурации белков очевиден –
по мере повышения температуры атомы в молекуле белка приобретают
все более высокую энергию, в том числе кинетическую, и, в конце концов, становится возможным разрушение слабых связей, стабилизирующих глобулярную структуру белка, что и приводит к его инактивации.
12.4. ТЕРМИЧЕСКАЯ ИНАКТИВАЦИЯ ФЕРМЕНТОВ
Термическая инактивация ферментов может быть обратимой, необратимой или смешанной. Зависимость скорости реакции ферментативного
катализа от температуры в достаточно широком диапазоне температур
может быть описана с помощью простой модели обратимой термической
инактивации. Согласно этой модели, мы принимаем, что неактивная (in-
282
Рисунок 143 – Термическая инактивация фермента каталаза – температурная
зависимость логарифма скорости разложения Н2О2
Хотя изолированные водородные связи сравнительно слабы (их
энергия обычно 3–7 ккал/моль), энтальпия инактивации ферментов ΔH d
283
достаточно высока, составляя, например, для трипсина и лизоцима белка
куриных яиц соответственно 68 и 73,5 ккал/моль. Инактивация этих
ферментов
сопровождается
изменением
энтропии,
равным
+213 ккал/(моль⋅К). Благодаря высокой энтальпии денатурации уже небольшие изменения температуры существенно изменяют относительное
количество активной формы фермента. При таких высоких значениях
ΔH d фермент инактивируется практически полностью в диапазоне три-
сящий от температуры предэкспоненциальный множитель. Подробнее
теория переходного состояния (теория абсолютных скоростей реакций
Эйринга и Поляни изложена в §ХI.2 учебника А.Г. Стромберг,
Д.П. Семченко, Физическая химия, М.: Высшая школа, 2001). Подставляя
в уравнение wmax = k (T )[ E ] act выражения для k (T ) и [ E] act , получим
дцати градусов.
Поскольку весь фермент существует либо в активной, либо в неактивной форме
[ E ] inact
= K d следует, что
[ E ] act
[ E ] act =
Согласно
теории
k1
k2
[ E ]0
.
1+ Kd
переходного
состояния,
скорость
реакций
k−1
том соотношения Ε a = ΔH ≠ + RT может быть выражена следующим образом
wmax = k (T )[ E ]act ,
1
⎛ Ε ⎞
тангенс угла наклона кривой приближенно равен ⎜ − a ⎟ .
T
⎝ R ⎠
Тангенс угла наклона другого прямого участка кривой при более высоких
значениях
⎛ ΔH d − Ε a ⎞
температурах приблизительно равен ⎜
⎟.
R
⎝
⎠
Величину ΔS d можно определить, используя тот факт, что при темTmax , когда
ln wmax
принимает наивысшее значение и
d
ln wmax = 0 . Поэтому можно рассчитать константу равновесия
dT
⎞
⎟.
⎠
Здесь k B – постоянная Больцмана; h – постоянная Планка; α – не зави284
ределения на основе тех же экспериментальных данных. При больших
пературе
где
⎛ ΔS ≠ ⎞
⎞
⎛ Εa
exp
⋅
⎜
⎟ ⋅ exp ⎜ −
⎟
R
⎠
⎝ RT
⎝
⎠
.
Ε a =3,5 ккал/моль, ΔS d =168 ккал/(моль⋅К), β =258 мм3/мин после их оп-
E + S → ES и ES → E + P при высоких концентрациях субстрата и с уче←
⎛k T
k (T ) = α ⎜ B
⎝ h
⎞
⎟
⎠
⎛ ΔS ≠ ⎞
⎟.
Здесь коэффициент β включает α , k B , h0 , [E ] 0 и exp⎜⎜
⎟
⎝ R ⎠
Это уравнение и представляет собой схематично изображенное на
рисунке 44 поведение системы фермент-субстрат. Сплошная кривая на
этом рисунке, проходящая через экспериментальные точки, была вычислена при следующих значениях параметров: ΔH d =55,5 ккал/моль,
[ E ] 0 = [ E ] act + [ E ] inact ,
то из уравнения
wmax
⎛ Ε ⎞
β ⋅ T ⋅ exp ⎜ − a ⎟
⎝ RT ⎠
=
⎛ ΔH d ⎞
⎛ ΔS d
1 + exp ⎜ −
⎟ ⋅ exp ⎜
⎝ RT ⎠
⎝ R
K d (Tmax ) =
Ε a + RTmax
,
ΔH d − Ε a − RTmax
поскольку Tmax известна из измерений, а величины Ε a и ΔH d мы уже оп285
ределили. Зная величину K d (Tmax ) , мы найдем ΔS d из соотношения
⎛ ΔH d ⎞
⎛ ΔS d ⎞
K d = exp ⎜ −
⎟ ⋅ exp ⎜
⎟ . Наконец подберем такое значение коэффи⎝ RT ⎠
⎝ R ⎠
циента β , чтобы wmax (Tmax ) стало равным измеренной величине.
При необходимости более точные значения параметров можно получить методом последовательного приближения.
В частности, очень большое влияние на результаты может оказывать значение Tmax . Конечно, от температуры зависят и другие параметры
уравнений скорости реакции, например, константа Михаэлиса, K M , или
константы диссоциации K S и K I .
Если эти параметры считать константами равновесия K , как это
часто бывает в действительности, то мы должны прийти к температурной
зависимости аналогичной зависимости wmax (T ) . Тогда график зависимо1
будет представлять собой прямую линию, по наT
клону которой можно определить стандартную свободную энергию.
В некоторых случаях графическая зависимость в этих координатах
нелинейная.
Причиной подобных осложнений могут быть неоправданные упрощения в интерпретации K S или K I , или даже в последовательности ката-
сти ln K (или рК) от
лизируемых ферментом реакций.
Напомним, например, что для случая простейшей последовательноk1
k2
сти реакций E + S → ES и ES → E + P константа Михаэлиса K M =
←
k−1
k −1 + k 2
k1
представляет собой не что иное, как отношение констант скоростей элементарных реакций.
Если каждую из этих констант элементарных стадий в свою очередь
⎛ Ε ⎞
выразить в форме уравнения Аррениуса k = A exp⎜ − a ⎟ или в форме
⎝ RT ⎠
⎛k T
уравнения k (T ) = α ⋅ ⎜ B
⎝ h
⎛ ΔS ≠ ⎞
⎞
⎛ Εa ⎞
⎟ ⋅ exp ⎜ −
⎟ ⋅ exp ⎜
⎟ теории переходного
R
RT ⎠
⎠
⎝
⎝
⎠
286
состояния, то получится весьма сложная форма зависимости от температуры.
Другим возможным источником затруднений в определении зависимости некоторых параметров скорости реакции от температуры может
служить
существование
нескольких
промежуточных
ферментсубстратных комплексов (или комплексов фермента с продуктом реакции).
Подобные соображения были положены в основу полезного и довольно широко применяемого способа проверки корректности кинетических моделей и соответствующих гипотетических последовательностей
реакций.
Если зависимость кинетических параметров в аррениусовских координатах выражается не прямой, то исходная модель или чрезмерно упрощена, или вообще неверна.
12.5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ КИНЕТИКИ
ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
Наиболее употребительные в кинетике ферментативных реакций
экспериментальные методы классифицируют по способу проведения изучаемой реакции и в зависимости от того, каким образом следят за концентрацией реагирующих веществ.
С этих точек зрения различают методы классические, проточные,
методы остановки потока и релаксационные.
Классические методы. В классических методах исследования кинетики за смесью реагирующих веществ и изменением их концентраций наблюдают либо периодически (например, путем отбора проб и их анализа),
либо непрерывно (измерением величин, пропорциональных концентрациям).
Время, необходимое для полного перемешивания реагирующих веществ перед началом реакции, должно быть достаточно малым по сравнению с полупериодом протекания реакции – временем необходимым для
преобразования половины молекул субстрата в продукт.
287
Отсюда следует, что классические методы пригодны для исследования только реакций с полупериодом более нескольких секунд. Реакции с
более коротким полупериодом этими методами можно изучать лишь при
малых концентрациях или при пониженных температурах.
Из методов непрерывного измерения физических величин, зависящих от концентрации реагирующих веществ, необходимо в первую очередь упомянуть прямой спектрофотометрический метод.
В ферментативных реакциях изменения поглощения, позволяющие
различать исходные вещества и продукты реакции, вполне измеримы.
При этом успешно пользуются регистрирующими спектрофотометрами,
записывающими кинетическую кривую в виде зависимости поглощения
при данной длине волны от времени. Можно воспользоваться и тем, что
спектры кофермента после реакции и перед реакцией различаются, как,
например, в случае NADH и NAD+.
Очень близок к спектрофотометрическому методу метод измерения
флуоресценции.
Многие коферменты сильно флуоресцируют и притом в ничтожных
концентрациях. Поэтому метод измерения флуоресценции особенно пригоден при работе с малыми концентрациями фермента и субстрата. Именно так поступают при измерении констант K M и K I в случае высокого
Необходимым условием индикаторного метода является значительное превышение скорости реакции индикатора с субстратом или продуктом над скоростью реакции Субстрат → Продукты (иначе, исследоваться
будет не кинетика ферментативной реакции, а кинетика реакции индикатора с субстратом или продуктом). Необходимо также, чтобы индикатор
не оказывал влияния на скорость ферментативной реакции (был нейтральным компонентом среды).
сродства фермента к субстрату и ингибитору.
Если при ферментативной реакции происходит выделение или потребление ионов водорода (протонов), для её исследования используют
потенциостат.
За протеканием реакции следят, измеряя количество кислоты или
основания, требуемое для поддержания постоянного значения рН реакционной смеси. Схема такого устройства изображена на рисунке 144.
Если при ферментативной реакции исходные вещества или продукты быстро и обратимо реагируют с посторонними молекулами, обнаруживающими интенсивный спектр поглощения, можно воспользоваться
индикаторным методом. Для контроля кинетики реакции наблюдают изменения спектра посторонних молекул, обусловленные изменением концентрации субстрата или продукта.
Измерение оптического вращения часто использовали в прошлом;
метод сохраняет свое значение при исследовании кинетики ферментативных процессов и в настоящее время. Огромное большинство биологических соединений и продуктов, встречающихся в ферментативных
реакциях, обладают оптической активностью. Большей чувствительности
метода удается обычно добиться измерением в ультрафиолетовой части
спектра.
При периодическом контроле кинетики реакций отбираемые пробы
реакционной смеси можно анализировать некоторыми методами, позво-
288
289
Рисунок 144 – Схема потенциостата для исследования кинетики ферментативных реакций
ляющими количественно определять реагирующие вещества или продукты. Однако после взятия пробы фермент необходимо быстро инактивировать, и притом так, чтобы не повлиять на концентрации субстрата и
продукта.
Методы непрерывного потока. Методы непрерывного потока
(continuous flow methods) или методы непрерывной струи, позволяют расширить область классических методов изучения кинетики до области с
полупериодом реакции в несколько микросекунд.
Принцип метода изображен на рисунке 145. Растворы обоих реагирующих веществ вводят с постоянной скоростью в специальную смесительную камеру, в которой полное смешивание реагирующих веществ
происходит в течение 1 мс. Полученный таким образом раствор реагирующих друг с другом веществ поступает далее в трубку с постоянным
сечением. В этой трубке на любом расстоянии от смесительной камеры
устанавливается стационарная концентрация, определяемая скоростью
потока, удалением от смесительной камеры и скоростью биохимической
реакции.
Рисунок 145 – Схема прибора для изучения кинетики ферментативных реакций
методом непрерывного потока (непрерывной струи)
Стационарную концентрацию веществ в данном месте трубки можно измерять подходящим способом (например, спектрофотометрическим,
290
термометрическим и т. п.). Если при методе непрерывного потока точно
известна скорость смешанного раствора в трубке, то можно точно определить и время, в течение которого протекала реакция от смесительной камеры до места измерения в трубке.
Например, если скорость струи в трубке равна 10 мс, то на расстоянии 1 см от смесителя "возраст" раствора будет равен 1 мс, на расстоянии
10 см – 10 мс и т. д. Это время также можно варьировать, меняя диаметр
трубки. Неудобством этого метода оказывается потребление значительного объема раствора, чтобы добиться равномерного потока во всем приборе. Поскольку при одном измерении получают только одну точку
зависимости концентрации от времени, то применение этого метода ограничено главным образом теми системами, для которых и субстрат, и фермент доступны в больших количествах.
Метод остановленной струи. В методе остановленной струи (другое название – метод прерывного потока) реагирующие вещества быстро
смешивают в специальной смесительной камере и измеряют их концентрации. После основательного перемешивания поток раствора через реакционный сосуд прекращают и при помощи быстрого регистрирующего
устройства – например, оптического детектора с осциллографической записью – наблюдают в выбранной точке реакционной трубки снижение
концентрации веществ со временем.
Для остановки струи используют простое устройство, которое позволяет остановить поток за 1–2 мс. Это устройство представляет собой
поршень запорного насоса, помещенный в конце трубки. Реакционная
смесь толкает этот поршень, и он резко останавливается, дойдя до внешних ограничителей и замкнув контакты, включающие регистрацию (рисунок 146).
Для метода остановленной струи несущественно точное регулирование расхода жидкости, но важно, чтобы оба раствора были смешены
очень быстро и чтобы время, протекающее между смешиванием растворов и заполнением наблюдательной кюветы, было бы возможно меньше
времени протекания исследуемой реакции. Наблюдение за реакцией начинается в момент, когда прекращается поток и включается регистрация.
291
Преимущество описанного метода по сравнению с непрерывным заключается главным образом в меньшем расходе реагирующих веществ.
Рисунок 146 – Схема прибора для изучения кинетики ферментативных реакций
методом остановленной струи (прерывного потока)
Релаксационные методы. К этой группе относятся весьма универсальные методы исследования кинетики быстрых химических реакций.
Принцип релаксационных методов состоит в следующем. В системе, в которой установилось равновесие всех химических реакций, кинетику которых следует изучить, производят быстрое однократное или периодически
повторяющееся изменение одной или нескольких интенсивных величин,
определяющих равновесие (например, температуры или давления). В результате этого изменения произойдет сдвиг химического равновесия из
исходного в новое равновесное состояние и, следовательно, изменение
концентраций реагирующих веществ.
Изменение концентраций можно контролировать удобным, достаточно быстрым способом. При этом обычно наблюдают изменения некоторых физических величин, как правило, таких, которые являются
линейными функциями концентрации (например, оптическое поглощение).
Из предположения, что скорость изменения интенсивной величины
во много раз выше скорости исследуемой химической реакции, следует,
292
что происходит запаздывание изменения концентраций – релаксационный
эффект. В случае однократного изменения интенсивной величины получают релаксационный отсчет, содержащий временную характеристику
исследуемой реакции – время релаксации. Это время является функцией
констант скорости отдельных реакций и равновесных концентраций реагирующих веществ. Из зависимости времени релаксации от равновесных
концентраций можно определить механизм реакции и значения констант
отдельных реакций.
При анализе механизмов ферментативных реакций наибольшее
применение нашел метод температурного скачка. Это объясняется тем,
что разработана достаточно простая и надежная аппаратура, позволяющая
осуществить изменение температуры за несколько микросекунд, а также
тем, что данный метод позволяет работать с небольшим объемом исследуемого раствора (до 0,1 мл).
Раствор инкубируют в кювете спектрофотометра или флуориметра,
а затем менее чем за 1 мкс повышают температуру на 5–10 градусов с помощью разряда конденсатора (или за 10–100 нс с помощью инфракрасного лазера).
Схема устройства для измерений методом температурного скачка
изображена на рисунке 147.
Рисунок 147 – Схема прибора для изучения кинетики ферментативных реакций
методом температурного скачка
293
В этом устройстве конденсатор высокого напряжения заряжается от
источника высокого напряжения. Затем конденсатор разряжают искровым
разрядником через измерительную кювету с исследуемым раствором за
время полрядка 1 мкс. Для того, чтобы так быстро разрядить конденсатор,
необходимо использовать электролит достаточной электропроводности.
Это условие особенно хорошо выполняется в ферментативных реакциях,
в которых для проявления оптимальной активности необходима повышенная концентрация электролита (~1 М).
Изменение концентрации в релаксирующей системе измеряют спектрофотометрически. От источника света через монохроматор в кювету
пропускают пучок света выбранной длины волны. С помощью полупрозрачного зеркала часть пучка отводится для сравнения. Оба луча – луч
сравнения и луч, прошедший через исследуемый раствор, – поступают на
фотоумножители и получаемые сигналы подаются на дифференциальный
усилитель и быстрый осциллограф. По сравнению с другими способами
спектрофотометрический имеет то преимущество, что, подбирая соответствующую длину волны, можно наблюдать изменения концентрации любых веществ в релаксирующей смеси.
Если исследуемый биохимический процесс не сопровождается непосредственно изменением поглощения раствора, его можно объединить
с какой-нибудь другой реакцией, вызывающей изменение поглощения и
протекающей быстрее, чем та стадия, которая определяет общую скорость биохимической реакции.
Переход системы к новым равновесным концентрациям реагентов
называется "химической релаксацией". Если отклонение от равновесия,
вызванное внешним воздействием, невелико, кинетика релаксации будет
описываться линейным дифференциальным уравнением.
Рассмотрим принципы релаксационной кинетики на примере простейшей реакции образования комплекса фермента E с каким-либо лигандом A (субстратом или эффектором)
k1
В начальном состоянии система находится в равновесии, которое
характеризуется равновесным концентрациями [E ] , [ A] , [EA] и константой равновесия
K=
[ EA]
.
[ E ][ A]
Предположим, что в системе резко изменяется температура
( T → T + ΔT ). Это приводит к изменению константы равновесия
( K → K + ΔK ), которое определяется термодинамическим соотношением
ΔK
ΔH
≅ Δ ln K ≅
ΔT .
K
RT 2
После быстрого изменения температуры исходные концентрации
компонентов не соответствуют новому равновесию, характеризующемуся
константой K + ΔK , и, следовательно, система должна перейти в новое
равновесное состояние. При этом кинетика реакции описывается дифференциальным уравнением
d[ EA]
= k1 [ E ][ A] − k −1 [ EA] .
dt
Это уравнение нелинейно, поскольку содержит произведение переменных [ E ] ⋅ [ A] . Анализ кинетики существенно упрощается, если отклонение от равновесия, вызываемое внешним фактором, невелико, т. е.,
[ E ] Δ[ E ] , [ A] Δ[ A] .
В этом случае, подставляя вместо [E ] , [ A] , [EA] , соответственно,
[ E ] + Δ[ E ] , [ A] + Δ[ A] , [ EA] + Δ[ EA] можно пренебречь произведением
( Δ[ E ] ⋅ Δ[ A] ).
С учетом равенства Δ[ A] = Δ[ E ] = − Δ[ EA] (из материального баланса) дифференциальное уравнение становится линейным дифференциальным уравнением с постоянными коэффициентами и принимает вид
E + A→
← EA .
d(Δ[ EA])
+ (k1 ([ E ] + [ A]) + k −1 )Δ[ EA] = k1 [ E ][ A] − k −1 [ EA] .
dt
294
295
k −1
Решение этого дифференциального уравнения представляет собой
экспоненциальную функцию Δ[EA] от времени, в которой показатель
экспоненты связан с элементарными константами скорости реакции
ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОКОНТРОЛЯ
1. Запишите выражение для [ ES] стац – предела, к которому стремится концентрация фермент-субстратного комплекса в предстационарном режиме.
k1
→
E + A←
EA уравнением
k−1
1
= k1 ([ E ] + [ A]) + k −1 .
τ
Величина τ называется временем релаксации. При анализе зависимости времени релаксации от равновесных концентраций фермента [E ] и
лиганда [ A] могут быть найдены элементарные константы скорости реакk1
→
EA .
ции E + A←
k−1
Внешнее влияние, возмущающее систему, может иметь разную физическую природу. В общем случае константа равновесия является функцией не только температуры, но и давления, электрического поля.
Поэтому помимо рассмотренного метода (температурного скачка) внешнее воздействие на систему можно осуществить, изменяя давление (скачок давления, поглощение ультразвука) или электрическое поле (метод
электрического импульса). Релаксационные методы имеют весьма высокую разрешающую способность (Таблица 11).
k1
k2
k−1
k−2
2. Для случая каталитической реакции E + S → ES → E + P при
← ←
большом избытке субстрата ( [ S ]0 [ E ]0 ) [ S ] ≈ [ S ]0 и небольшой
глубине реакции ( [ P] ≈ 0 ) показать, что в предстационарном режиме зависимость концентрации фермент-субстратного комплекса от времени описывается выражением
[ E ]0 [S ]0
(1 − exp{−k1 ([ S ] 0 + K M ) ⋅ t}) .
[ ES ] =
K M + [S ]0
k1
k2
k−1
k−2
3. Для случая каталитической реакции E + S → ES → E + P при
← ←
большом избытке субстрата ( [ S ]0 [ E ]0 ) [ S ] ≈ [ S ]0 и небольшой
глубине реакции ( [ P] ≈ 0 ) показать, что в предстационарном режиме при [ S ]0 K M
зависимость концентрации фермент-
субстратного комплекса от времени описывается выражением
[ ES ] = [ E ] 0 (1 − exp{−k1 [ S ] 0 ⋅ t}) .
Таблица 11 – Разрешающая способность релаксационных методов
Метод
Поглощение ультразвука
Температурный скачок
Метод электрического импульса
Скачок давления
Разрешающая способность, с
10–6 – 10–10
10–4 – 10–6
10–4 – 10–6
10–2
Видно, что применение методов релаксационной кинетики позволяет исследовать процессы с временем релаксации до 10–10 с. Именно
поэтому релаксационная кинетика широко используется при исследовании механизмов быстрых ферментативных реакций.
296
k1
k2
k−1
k−2
4. Для случая каталитической реакции E + S → ES → E + P при
← ←
большом избытке субстрата ( [ S ]0 [ E ]0 ) [ S ] ≈ [ S ]0 и небольшой
глубине реакции ( [ P] ≈ 0 ) показать, что в предстационарном режиме при [ S ]0 K M
зависимость концентрации фермент-
субстратного комплекса от времени описывается выражением
[ E ]0 [S ]0
(1 − exp{−k1 K M ⋅ t}) .
[ ES ] =
KM
297
5. Как определяют константу k1 по предстационарной кинетике
ферментативной реакции?
6. Как определяют сумму констант (k −1 + k 2 ) по предстационарной
кинетике ферментативной реакции?
7. Как определяют константу k 2 по стационарной кинетике фер-
СПИСОК ЛИТЕРАТУРЫ
ментативной реакции?
8. Как определяют константу k −1 по предстационарной кинетике
ОСНОВНАЯ
ферментативной реакции?
k1
k2
k−1
k−2
9. Для случая каталитической реакции E + S → ES → E + P при
← ←
большом избытке субстрата ( [ S ]0 [ E ]0 ) [ S ] ≈ [ S ]0 и небольшой
глубине реакции ( [ P] ≈ 0 ) показать, как из кинетики накопления
фермент-субстратного комплекса [ES ] определить константу
скорости k1 и сумму констант скоростей (k −1 + k 2 ) .
298
1. Огурцов А.Н. Введение в биофизику. Физические основы биотехнологии / А. Н. Огурцов. – Х. : НТУ "ХПИ", 2008. – 320 с.
2. Огурцов О.М. Молекулярна біофізика ферментів / О.М. Огурцов. – Х. :
НТУ "ХПІ", 2009. – 192 с.
3. Огурцов А.Н. Механизмы ферментативных реакций / А.Н. Огурцов. –
Х. : НТУ "ХПИ", 2004. – 75 с.
4. Огурцов А.Н. Кинетика ферментативных реакций / А.Н. Огурцов. –
Х. : НТУ "ХПИ", 2007. – 146 с.
5. Березин И.В. Основы физической химии ферментативного катализа /
И.В. Березин, К. Мартинек. – М. : Высшая школа, 1977. – 280 с.
6. Фершт Э. Структура и механизмы действия ферментов / Э. Фершт. –
М. : Мир, 1980. – 432 с.
7. Варфоломеев С.Д. Биокинетика: Практический курс / С.Д. Варфоломеев, К.Г. Гуревич. – М. : ФАИР-Пресс, 1999. – 720 с.
8. Березин И.В. Практический курс химической и ферментативной кинетики / И.В. Березин, А.А. Клесов. – М. : Изд. МГУ, 1976. – 320 с.
9. Калоус В. Биофизическая химия / В. Калоус, З. Павличек. – М. : Мир,
1985. – 446 с.
10. Бейли Дж., Оллис Д. Основы биохимической инженерии. Пер. с англ. в
2-х частях. Ч.1. – М. : Мир, 1989. – 692 с.
11. Маршелл Э. Биофизическая химия / Э. Маршелл. – М. : Мир, 1981. –
806 с.
12. Эткинс П. Физическая химия / П. Эткинс. М. : Мир, 1980. – 580 с.
13. Біофізика / За ред. П.Г. Костюка. – К. : Обереги, 2001. – 544 с.
14. Protein Data Bank. – Интернет-ресурс. – http://www.pdb.org/
299
15. Волькенштейн М.В. Биофизика / М.В. Волькенштейн. – М. : Наука,
1988. – 592 с.
16. Рубин А.Б. Биофизика : В 2 т. Т.1 / А.Б. Рубин. – М. : Наука, 2004.–
448 с.
17. Владимиров Ю.А. Биофизика / Ю.А. Владимиров, Д.И. Рощупкин,
А.Я. Потапенко, А.И. Деев. – М. : Медицина, 1983. – 272 с.
18. Molecular Cell Biology / H. Lodish, A. Berk, L.S. Zipursky et al. – New
York : Freeman, 2003. – 572 p.
19. Goodsell D.S. Bionanotechnology: Lessons from nature / D.S. Goodsell. –
New Jersey : Wiley, 2004. – 337 p.
20. Finkelstein A.V. Protein Physics / A.V. Finkelstein, O.B. Ptitsyn . – London : Academic Press, 2002. – 354 p.
21. Koolman J. Color Atlas of Biochemistry / J. Koolman, K.H. Roehm. –
Stuttgart : Thieme, 2005. – 467 p.
ДОПОЛНИТЕЛЬНАЯ
22. Глик Б. Молекулярная биотехнология. Принципы и применение /
Б. Глик, Дж. Пастернак. – М.: Мир, 2002. – 589 с.
23. Leskovac V. Comprehensive Enzyme Kinetics / V. Leskovac. – New York :
Kluwer Academic Publishers, 2004. – 438 p.
24. Огурцов А.Н. Введение в молекулярную биотехнологию / А.Н. Огурцов. – Х. : НТУ "ХПИ", 2008. – 152 с.
25. Огурцов А.Н. Молекулярная биоэнергетика клетки / А.Н. Огурцов. –
Х. : НТУ "ХПИ", 2009. – 112 с.
26. Огурцов А.Н. Электрогенез биомембран и механизмы мембранной
сигнализации / А.Н. Огурцов, О.Н. Близнюк. – Х. : НТУ "ХПИ", 2010.
– 224 с.
27. Огурцов А.Н. Введение в бионанотехнологию / А.Н. Огурцов. – Х. :
НТУ "ХПИ", 2010. – 136 с.
28. Огурцов А.Н. Основы молекулярной биологии. Ч. 1. Молекулярная
биология клетки / А. Н. Огурцов. – Х. : НТУ "ХПИ", 2010. – 304 с.
29. Огурцов А.Н. Нанобиотехнология. Основы молекулярной биотехнологии / А.Н. Огурцов. – Х. : НТУ "ХПИ", 2010. – 384 с.
300
СОДЕРЖАНИЕ
Вступление
Раздел I. Теоретические основы биокатализа
Глава 1. Катализ и биокатализ
1.1. Основные понятия энзимологии
1.2. Специфика биокатализаторов
1.3. Энергетика биохимических реакций
1.4. Основные понятия химического катализа
Глава 2. Классификация ферментов
2.1. Основы классификации ферментов
2.2. Оксидоредуктазы
2.3. Трансферазы
2.4. Гидролазы
2.5. Лиазы
2.6. Изомеразы
2.7. Лигазы
Глава 3. Строение аминокислот
3.1. Классификация аминокислот
3.2. Специальные аминокислоты
3.3. Неполярные и ароматические аминокислоты
3.4. Полярные незаряженные аминокислоты
3.5. Заряженные аминокислоты
Глава 4. Строение белков
4.1. Первичная структура белка
4.2. Вторичная структура белка
4.3. Третичная структура белка
4.4. Четвертичная структура белка
4.5. Фолдинг белков
4.6. Механизмы регуляции фолдинга
301
3
5
5
5
7
11
19
25
25
27
32
35
39
42
44
46
46
51
55
60
63
68
68
70
75
78
79
88
Глава 5. Физические взаимодействия в ферментах
5.1. Особенности ковалентных связей
5.2. Нековалентные взаимодействия
5.3. Гидрофобный эффект
92
93
96
108
Раздел II. Механизмы ферментативных процессов
Глава 6. Биокатализ
6.1. Специфика ферментативных реакций
6.2. Фосфорилирование белков ферментом протеин-киназа А
6.3. Особенности функционирования ферментов
Глава 7. Механизмы ферментативного катализа
7.1. Механизмы регуляции ферментативной активности
7.2. Механизмы ферментативных реакций
7.3. Абзимы
Глава 8. Примеры ферментативных процессов
8.1. Каталитический цикл лактатдегидрогеназы
8.2. Расщепление ацетилхолина ацетилхолинэстеразой
8.3. Расщепление полипептидных цепей сериновыми
протеазами
8.4. Структурные особенности ферментов
8.5. Ферментативные реакции гликолиза
116
116
116
124
127
139
139
150
162
168
168
173
Раздел III. Кинетика ферментативных реакций
Глава 9. Основы формальной кинетики
9.1. Особенность ферментативной кинетики
9.2. Гипотеза о стационарности
9.3. Одностадийная однокомпонентная прямая реакция
9.4. Прямая и обратная реакции
9.5. Последовательные реакции
9.6. Некатализируемая реакция с одним промежуточным
соединением
9.7. Каталитическая реакция с одним промежуточным
соединением
9.8. Пример решения задачи
190
190
190
192
194
195
198
302
175
181
185
Глава 10. Стационарная кинетика Михаэлиса-Ментен
10.1. Уравнение Михаэлиса
10.2. Приближение Лайнуивера-Берка
10.3. Смысл параметров кинетики Михаэлиса-Ментен
10.4. Снятие ограничений Михаэлиса-Ментен для случая
обратной реакции
10.5. Снятие ограничений Михаэлиса-Ментен для реакций с
числом промежуточных соединений больше одного
10.6. Мультисубстратные реакции
10.7. Снятие ограничений Михаэлиса-Ментен для
мультисубстратных реакции
Глава 11. Регуляция скоростей ферментативных реакций
11.1. Регуляция ферментативной активности
11.2. Конкурентное ингибирование
11.3. Неконкурентное и смешанное ингибирование
11.4. Метод Диксона
11.5. рН-регуляция скоростей ферментативных реакций
11.6. Аллостерическая регуляция скоростей ферментативных
реакций
11.7. Автоингибирование субстратом
Глава 12. Ферментативные реакции в нестационарном режиме
12.1. Нестационарная кинетика ферментативных реакций
12.2. Определение констант скоростей из нестационарной
кинетики
12.3. Влияние температуры на скорость реакций
12.4. Термическая инактивация ферментов
12.5. Экспериментальные методы исследования кинетики
ферментативных реакций
Список литературы
201
202
205
303
211
211
212
214
217
220
223
227
236
236
242
246
251
254
261
269
275
275
281
282
287
299
Навчальне видання
ОГУРЦОВ Олександр Миколайович
ФЕРМЕНТАТИВНИЙ КАТАЛІЗ
Навчальний посібник
для студентів напряму підготовки 051401 «Біотехнологія»,
в тому числі для іноземних студентів
Російською мовою
Відповідальний за випуск М.Ф. Клещев
Роботу до видання рекомендувала М.Г. Зінченко
В авторській редакції
План 2010 р., поз. 52 / 110 - 10
Підп. до друку 05.07.2010 р. Формат 60×84 1/16. Папір офісний. Riso-друк.
Гарнітура Таймс. Ум. друк. арк. 17,6. Наклад 300 прим.
Зам. № 319. Ціна договірна
Видавничий центр НТУ «ХПІ».
Свідоцтво про державну реєстрацію ДК № 3657 від 24.12.2009 р.
61002, Харків, вул. Фрунзе, 21
Друкарня НТУ «ХПІ». 61002, Харків, вул. Фрунзе, 21