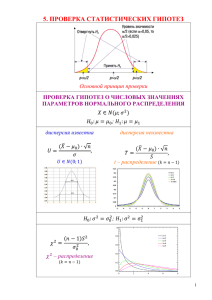
Проверка статистических гипотез является одной из основных задач математической статистики

Проверка статистических гипотез является одной из основных задач математической
статистики. Суть этой задачи состоит в том, что на основании выборочных данных
должно быть принято или отвергнуто некоторое предположение (статистическая
гипотеза) относительно генеральной совокупности.
Процедура сопоставления гипотезы с выборочными данными называется проверкой
гипотез.
Задача статистической проверки ставится в следующем виде: относительно
некоторой генеральной совокупности высказывается та или иная гипотеза
. Из
генеральной совокупности извлекается выборка. Требуется указать правило, при
помощи которого можно было бы по выборке решить вопрос, следует ли принять
гипотезу
, либо отклонить ее. Например, эффективнее ли лекарство, испытанное
на определенном числе людей, по сравнению с другими способами лечения?
Аналогично можно поставить вопрос о новых правилах приема в вуз, методах
обучения, преимуществах новой разрабатываемой техники т.п.
Выдвигаемая гипотеза может быть правильной или неправильной, поэтому возникает
задача ее проверки.
Итак, под статистической гипотезой будем понимать всякое высказывание о
генеральной совокупности, проверяемое по выборке.
Статистические гипотезы делятся на параметрические (гипотезы о параметрах
распределения) и непараметрические(о виде неизвестного распределения).
Например:
· Математическое ожидание
гипотеза)
· Дисперсия
равно конкретному числу
равна конкретному числу
(параметрическая
(параметрическая);
· Генеральная совокупность распределена по нормальному закону
(непараметрическая);
и т.д.
, чтобы проверить нулевую гипотезу
относительно альтернативной
. Критерием статистической гипотезыназывается правило, которое позволяет
принять или отвергнуть нулевую гипотезу. При построении этого правила используют
некоторую функцию (статистику) от результатов наблюдения
), которая называется статистикой критерия.
Основной принцип проверки гипотез состоит в следующем. Множество возможных
значений статистики критерия
разбивается на два непересекающихся
подмножества: критическую область
, т.е. область отклонения гипотезы
область
принятия этой гипотезы. Если фактически полученное по выборке
значение статистики критерия попадает в критическую область, то основная гипотеза
отклоняется, и принимается альтернативная гипотеза
попадает в
, то принимается
,
отклоняется.
. Если значение критерия
При проверке гипотезы могут быть допущены ошибки двух типов:
Ошибка первого рода состоит в том, что отвергается нулевая гипотеза, когда на
самом деле она верна.
Ошибка второго рода возникает, когда отвергается альтернативная гипотеза
когда на самом деле она верна.
Вероятность ошибки первого рода (обозначается
значимости критерия:
Чем меньше
) называется уровнем
, тем меньше вероятность отклонить верную гипотезу. Допустимую
ошибку первого рода обычно задают заранее. Обычно для
стандартные значения
используют
=0,05; 0,01; 0,005; 0,001.
Вероятность ошибки второго рода (обозначается
Величину
,
):
, т.е. вероятность недопущения ошибки второго рода (отвергнуть
неверную гипотезу
, принять верную
), называют мощностью критерия.
Чем больше мощность критерия, тем меньше вероятность ошибки второго рода.
Последствия ошибок 1-го, 2-ого рода совершенно различны, в чем можно убедиться
на таких примерах:
- применительно к радиолокации говорят, что
– вероятность ложной тревоги;
- применительно к производству –
– вероятность пропуска сигнала,
– риск поставщика (т.е. забраковка по выборке
всей партии изделий, удовлетворяющих стандарту),
– риск потребителя (т.е.
прием по выборке всей партии изделий, не удовлетворяющих стандарту);
- применительно к судебной практике, ошибка 1-ого рода приводит к оправданию
виновного, ошибка 2-ого рода - осуждению невиновного.
В общем случае, при принятии решения возможны варианты, представленные в
таблице 4.2.
Отметим, что одновременное уменьшение ошибок 1-ого и 2-ого рода возможно лишь
при увеличении объема выборок. Поэтому обычно при заданном уровне значимости
отыскивается критерий с наибольшей мощностью.
Таблица 4.2.
Варианты принятия решения и соответствующие им ошибки
Гипотеза
Верна
Неверна
Наш выбор
Принимается
Правильное решение
Ошибка II рода
Отвергается
Ошибка I рода
Правильное решение